未知环境下室内轮式机器人路径规划算法

李 轩，刘晓东，石祥滨

(沈阳航空航天大学 a.电子信息工程学院； b.计算机学院，沈阳 110136)

随着移动机器人技术的不断发展，其应用领域已经拓展到人们的日常生活中，这对移动机器人自主运动的要求不断提高。作为自主运动的基础，路径规划成为移动机器人研究领域的一个重要分支[1-3]。路径规划是指在移动机器人的工作空间中搜索出一条以初始状态为起点、目标状态为终点，按照某种性能指标(如时间、距离、能量等)最优或次优的无碰撞路径[4-5]。目前，路径规划根据环境信息的掌握程度分为两种，一是在环境信息已知情况下的静态路径规划，无法在具有动态因素的环境中进行路径规划；二是在环境信息未知或者部分未知情况下，通过传感器获取环境信息从而进行动态路径规划[6-8]，其可有效地躲避环境中的动态因素。

快速扩展随机树(Rapidly-exploring Random Tree，RRT)算法是静态路径规划主流方法之一，其避免了静态路径规划需要对环境进行建模的过程，具有计算量小且速度快等优点[9]，但是RRT算法依据随机采样进行扩展导致其具有较大的随机性。研究者针对RRT算法随机性大的缺点对其进行改进[10-12]，有效降低了算法的随机性。人工势场法(Artificial Potential Field，APF)属于动态路径规划，其是一种通过构建虚拟力学势场进行路径规划的方法，在规划路径过程中易陷入局部最小值[13]，为克服此缺点有较多的改进方法[14-15]。

针对传统RRT算法，本文提出一种R-QRRT(Regional Quantitative RRT)算法，通过区域量化和方向引导降低RRT算法随机性，改善了节点分布，提高了算法效率。针对传统APF算法易陷入局部最小值的问题，本文提出了一种通过距离评估障碍物对机器人作用，选择性忽略某障碍物影响的D-APF(Distance APF)算法，使机器人快速逃离局部最小值点。对本文研究的室内未知环境下轮式机器人路径规划问题，提出R-QRRT算法和D-APF算法相结合的混合算法，通过传感器信息对环境中障碍物进行类型区分，当检测到存在动态障碍物时，通过D-APF算法进行局部路径规划，达到躲避动态障碍物目的；未检测到动态障碍物时，通过R-QRRT算法进行全局路径规划，最后在真实环境中验证了混合算法具有良好的路径规划效果。

1 机器人相关模型

本文研究内容主要针对基于二轮差速运动模型的室内轮式机器人，通过二维激光雷达获取环境信息。

1.1 运动学模型

二轮差速轮式机器人在运动控制方面有较高的灵活性，在进行路径规划时便于控制。二轮差速运动学模型如图1所示。

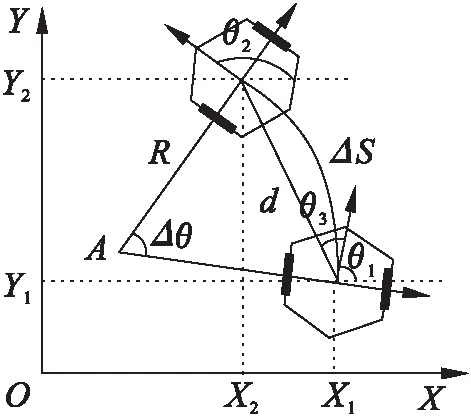
图1 二轮差速运动学模型

机器人在空间中一点的描述包括其位姿信息和运动状态，假设时刻t0机器人处于图中的A点，位姿为(xA,yA,θA)，(xA,yA)是当前的位置，θA是当前的航向角，线速度v、角速度ω为当前的运动状态。B点为时刻t0+△t机器人位置。根据图中几何关系，当△t趋向零时，得到机器人的运动学模型表达式，如式(1)所示。

(1)

其中，vL和vR为机器人左右轮子的速度。以A点为机器人的起始点，通过速度v和ω可以求得任意时刻t机器人的位姿如式(2)所示。

(2)

1.2 障碍物模型

路径规划任务的本质是躲避环境中的障碍物，因此需要对环境信息进行探测，建立障碍物模型。首先通过二维激光雷达获取障碍物点的距离与角度信息，并判断障碍物点是否属于同一障碍物以及统计障碍物个数，采用聚类的方法描述各障碍物信息，包括障碍物类型、障碍物可探测边缘的长度以及中心点，构建障碍物模型。通过构建关联性函数判断相邻时刻障碍物是否为同一障碍物以及类型。

二维激光雷达探测到障碍物点的角度信息为当前雷达转动角度，根据三角测距原理得到其距离信息，三角测距原理如图2所示。

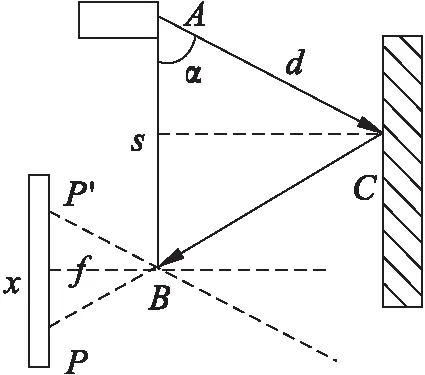
图2 三角测距原理

根据图2中相似三角形，有f/x=q/s，则点C与机器人的距离计算方法如式(3)所示。

(3)

在激光雷达探测过程中，设置自适应阈值σ，比较连续障碍点A与B的距离与该阈值的关系，判断点A与B是否属于同一障碍物。自适应阈值σ的取值表达式如式(4)所示。

σ=dsin(0.5°)

(4)

其中，0.5°为激光雷达的角度分辨率，d为当前测得障碍点的距离。当A与B的距离大于σ时判定出现新的障碍物，否则A与B属于同一障碍物。

采用聚类方法描述机器人当前时刻所探测到障碍物的信息，如式(5)所示。

(5)

其中，IDk(t)表示障碍物类型；Ck(t)表示探测到障碍物边缘线段的中心点；Sk(t)表示障碍物探测到边缘的长度。通过式(6)所示的关联性函数，判断相邻时刻障碍物是否为同一个障碍物以及其类型。

(6)

其中，λF、λG为系数，F为边缘线段中心点之间的距离，G为前后位置测到障碍物不重合部分长度占总长度的比例，计算方式如式(7)所示。

(7)

设置阈值c，进行相邻时刻探测到障碍物匹配工作，当C的取值大于该阈值时，判定障碍物OkI(t1)和Ok2(t2)为同一个障碍物。匹配工作之后，设置阈值csta、cdyn和ηk1对同一个障碍物的类型进行判断，判断规则如表1。

表1 障碍物类型判断规则

2 静态路径规划

以RRT算法为基础，针对其存在的随机性大的问题，提出R-QRRT算法， R-QRRT算法通过区域量化与方向引导，降低RRT算法的随机性、改善了树节点的分布，提高了算法的规划效率。在环境中不存在动态障碍物时，通过R-QRRT算法进行静态路径规划。

2.1 区域量化模型

由于RRT算法采样过程的随机性，使得算法在扩展过程中对已探索区域重复探索，产生较多的无用的树节点。本文对树节点周围空间进行量化，改善随机树节点分布情况，降低算法的随机性。量化模型如图3所示，随机树扩展点选取的规则如表2，根据量化模型和扩展点选取规则，随机树的节点之间的距离均大于扩展步长，在相同区域不会出现多个节点的情况。

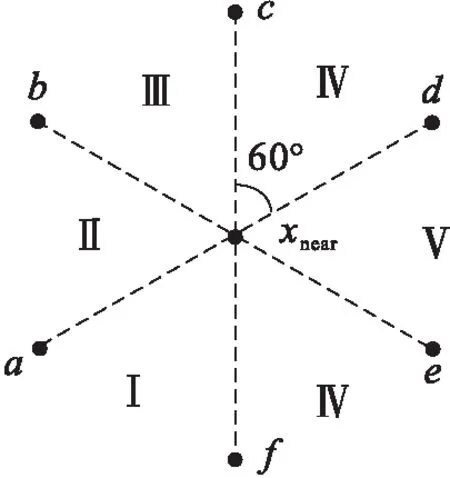
图3 区域量化模型

划分区域区域范围选取扩展点Ⅰ0～60度aⅡ60～120度bⅢ120～180度cⅣ180～240度dⅤ240～300度fⅥ300～360度e

2.2 R-QRRT算法原理

假设机器人工作空间为二维空间C，其中可自由移动空间为Cfree。在自由空间中选取路径规划的起始点xstart和目标点xgoal，满足条件xstart，xgoal∈Cfree。以起始点为根节点构建随机树Tk，其有k个节点且均位于自由空间。xi为随机树上的节点，即xi∈Tk，i=1,2,3,…，k。随机树扩展过程如图4所示。

图4 随机树扩展过程示意图

在工作空间中随机选取点xrand，判断xrand∈Cfree是否成立，如果其不成立则重新选取xrand。在树Tk上选取xnear，xnear满足Dis(xnear,xrand)≤Dis(xi,xrand)，式中Dis(a,b)函数表示空间中点a和b的几何距离，计算方法如式(8)所示。

(8)

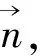
3 动态路径规划

APF算法有较好的实时性，且计算量相对于其他算法有明显优势，但易于陷入局部最小值点。本文提出D-APF算法，通过评估在局部最小值点对机器人影响最小的障碍物，已到达逃离最小值点的效果。在环境中具有动态障碍物时，采用D-APF算法进行动态路径规划，其原理如下。

D-APF算法将物理学中的势场理论引入到路径规划问题中，构建虚拟力学势场，虚拟力学势场分为以目标点为中心的引力场和以障碍物为中心的斥力场，机器人根据合力势场中受到的合力进行运动。引力场和斥力场函数如式(9)和(10)所示。

(9)

Urep(x)=

(10)

式中x表示机器人的位置，η和λ为引力尺度系数，d0为斥力场的有效范围。机器人在点x受到的引力和斥力如式(11)和(12)所示。

Fatt(x)=-Uatt(x)=ηDis(x,xgoal)

(11)

Frep(x)=-

(12)

引力和斥力分别指向目标点和机器人。上式中，▽d(x,xobs)为障碍物指向机器人的向量单位化，如式(13)所示。

(13)

机器人在某一位置所受的合力为斥力与引力的矢量之和，合力计算公式如式(14)所示。

(14)

图5为机器人在人工构造势场的受力情况示意图。

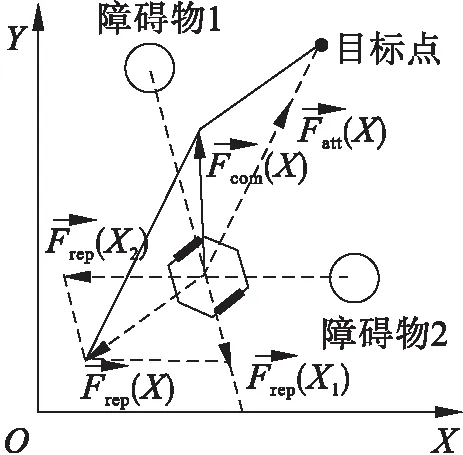
图5 机器人受力情况示意图

当机器人陷入局部最小值时，选择对机器人影响最小的第k个障碍物进行舍弃，该障碍物机器人的距离为d，舍弃后的合力表达式如式(15)所示。

(15)

机器人按照上述合力进行运动，机器人的运动方向指向第k个障碍物。当机器人运动距离到d/2时，恢复第k个障碍物的势力场对机器人的影响，保证机器人逃离局部最小值。

4 混合路径规划算法

通过传感器获取环境信息，当环境中不存在动态障碍物时，机器人根据R-QRRT算法规划出的静态路径进行移动，当机器人当前探测到环境中具有动态障碍物时，根据D-APF算法规划出路径进行移动，直至到达目标点。混合路径规划策略如图6所示。

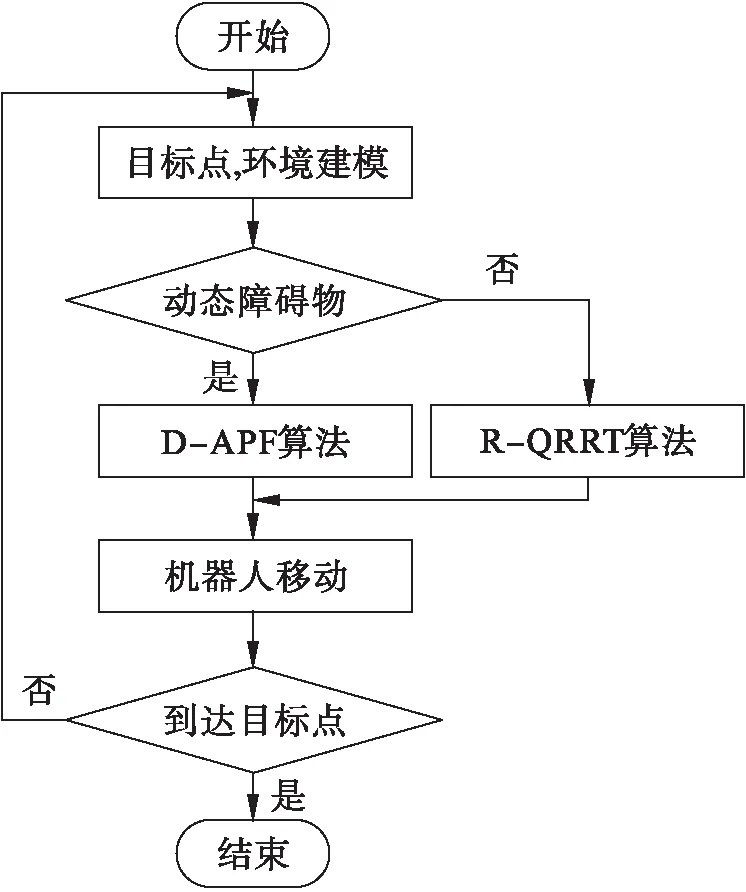
图6 机器人混合路径规划流程图

5 路径规划算法实验

实验部分分为仿真与真实环境实验两方面，仿真方面通过MATLAB软件分别对R-QRRT算法和D-APF算法进行仿真，真实环境实验使用二轮差速移动实验平台对混合算法的可行性和有效性进行验证。

5.1 R-QRRT算法MATLAB仿真

如图7所示，为三次不同起始点和目标点时传统RRT算法、RRT-Edge算法和R-QRRT算法MATLAB仿真结果。图中标注起始点和目标点，蓝色分支表示该次路径规划时生成的随机树，黑色线段为最终路径。表3为相应的随机树节点数目和规划时间。

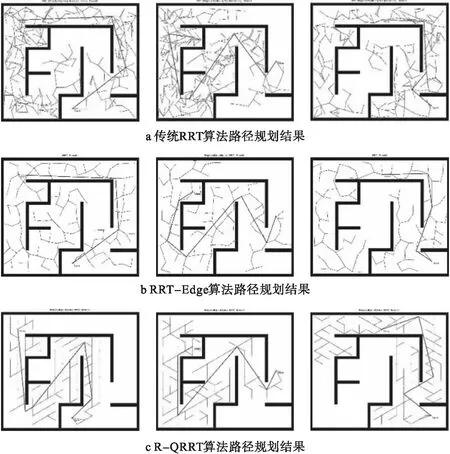
图7 传统RRT算法RRT-Edge改进RRT算法路径规划MATLAB仿真比较

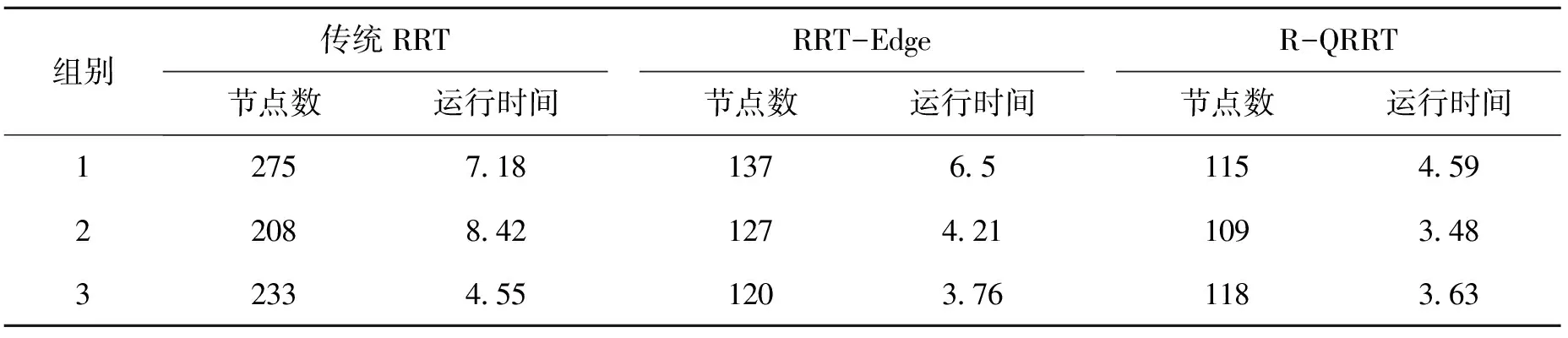
组别传统RRT节点数运行时间RRT-Edge节点数运行时间R-QRRT节点数运行时间12757.181376.51154.5922088.421274.211093.4832334.551203.761183.63

由图6和表3可以看出，R-QRRT算法与传统RRT算法相比，随机树节点的数量减少了50%左右，且改善了树节点在空间中的分布，不存在较多树节点位于相同区域的情况；提高了路径的搜索效率，提高算法的实时性。与RRT-Edge算法相比较，节点数量有小幅减少，但是在路径规划的效率上有明显的提高，证明本文提出的R-QRRT算法有效减少了节点数量，改善了节点分布并且提高了路径规划的效率。

5.2 D-APF算法MATLAB仿真

如图8为机器人根据人工势场法进行路径规划的仿真示意图，其中起始点为点(0,0)，目标点为(10,10)，图中存在障碍物A、B、C和D，障碍物A为动态障碍物，其余障碍物为静态障碍物，曲线为机器人移动轨迹。从图7可以看出，D-APF可以有效地解决在具有动态因素环境中的局部路径规划问题。

图8 人工势场法路径规划MATLAB仿真效果图

5.3 混合路径规划算法真实环境实验

本文主要研究室内环境未知情况下的路径规划问题，搭建如图9中的室内环境，采用本文提出的R_QRRT算法与D-APF算法相结合的混合算法进行起始点到目标点的路径规划。在初始位置，机器人探测到环境中的动态障碍物，采用R-QRRT算法进行路径规划，所得路径如图9路径1中曲线；机器人按照路径1运动到位置1，探测到环境中的动态障碍物，采用D-APF算法进行路径规划，所得路径如图9路径2中曲线；当机器人继续移动到达位置2时，动态障碍物占据机器人所规划路径，机器人重新规划路径，如图9路径3所示；机器人移动到位置3时，动态障碍物停止移动，机器人按照R-QRRT算法重新规划路径，如路径4所示；之后机器人经过位置4到达目标点，该过程中规划路径如路径5所示。

图9 真实环境下混合规划算法实验图

实验表明，在具有动态障碍物的室内未知环境中，混合路径规划算法能够实时通过传感器判断环境中是否存在动态障碍物，进而选取R-QRRT或D-APF算法进行路径规划，机器人按照规划路径安全无碰撞地从起始点移动到目标点。证明混合路径规划算法在具有动态障碍物的室内未知环境中具有有效性和可行性。

6 结论

对未知室内环境下轮式机器人路径规划问题的研究，其目的在于丰富轮式机器人路径规划算法，为轮式机器人在室内环境中提供一种行之有效的方法。本文提出的基于R-QRRT的静态路径规划和基于D-APF的动态路径规划相结合的混合算法不需要复杂的计算，易于实现。根据探测到的环境信息进行路径规划，在遇到不同类型障碍物时，采用不同的路径规划方法，能有效躲避障碍物并到达目标点。通过实验表明，该方法在实际环境中能够寻找到一条从起点到终点的安全路径，具有有效性和可行性。