热声激励下燃烧室热声固耦合特性数值研究

杨 光，田 晶， 艾延廷， 关 鹏，韩 斌

(1.沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室，沈阳110136；2.西北工业大学 动力与能源学院，西安 710072；3.中国航发沈阳黎明航空发动机有限责任公司 工装制造厂，沈阳 110034)

燃烧室内气体压力高频振荡是产生燃烧噪声的重要因素。燃烧噪声的强弱可以用燃烧室内压力的频谱曲线作为评定方法,所以准确获取燃烧室内压力频谱曲线对分析燃烧噪声有着重要的意义。

利用试验手段测试得到发动机燃烧室内的压力曲线来研究和分析燃烧噪声是目前常用的方法。房爱兵等[1]采用现场试验测试的手段对发动机燃烧噪声进行采集，分析合成气燃烧室在油气切换、燃烧合成气及合成气加湿过程燃烧噪声的变化趋势。魏凯等[2]依据噪声叠加原理，通过实验研究采集到噪声信号，并对其中的燃烧噪声和机械噪声进行分离。K.D.Artur等[3]进行预混燃烧下的热-声不稳定性分析，研究了温度场与声压力场的相互影响关系。基于试验测试得到高频振荡的燃烧室内压力曲线，而一般使用各种模拟软件计算得到的燃烧室内压力曲线均为光滑曲线。Huls R.等[4]基于声-弹性有限元模型和声振试验研究火焰筒壁面振动，并较好地预测了燃烧室内的声振水平。如果使用模拟软件计算后的光滑曲线评估燃烧噪声，则会带来很大的失真性。燃烧室实际噪声频率范围较宽，可视为多种频率声波的叠加，所以本文取单种频率的声波进行瞬态模拟研究分析。通过将入口条件设置为脉冲式入口，从而获得单种频率下的高频振荡的缸内压力曲线。通过研究不同频率下的声压波激励和结构响应之间的关系，分析结构振动与燃烧室内热声激励之间的影响规律。

燃烧室内的燃烧过程是一个复杂多变的物理、化学过程，本文以燃烧室内压力振荡和壁面响应为研究对象，以流固耦合的仿真技术为基础，建立了包含燃烧室结构和内部流场耦合的仿真模型。针对燃烧室内压力波造成的声压场变化问题，本文将燃烧理论与声学理论相结合，使用CFD软件来模拟压力波的传播。采用平面声波传播方程的解析解与CFD数值计算结果进行对比，验证了模拟方法的准确性。研究不同频率声压波动及火焰波型的影响规律，分析燃烧声波频率的改变对燃烧室结构动力学特性的影响规律，揭示了热-声作用对结构动力学特性的影响，为航空发动机及燃气轮机燃烧室设计提供参考。

1 双向耦合模型及原理

1.1 燃烧室结构建模

燃烧室结构如图1所示，燃烧室整体长为2 000 mm，燃烧室入口分为空气入口与燃气入口，其中空气入口直径为47 mm，两个燃气入口直径均为12 mm。本文模拟时间段内燃气进气质量流量不变，通过改变空气入口条件得到火焰脉冲50 Hz、55 Hz、60 Hz 3种工况下的燃烧过程，从而产生不同频率压力波动模拟声波与燃烧室壁面的双向耦合。燃烧室实际噪声频率范围宽，可视为多种频率声波的叠加，本文取单一频率的声波进行研究分析。

图1 结构及网格

数值研究中常采用的网格类型主要分为结构化网格与非结构化网格。结构化网格允许使用较少的网格单元并且计算量小，而非结构化网格具有更高的数值耗散率，对复杂几何模型流动更有利[5]。综合以上因素，燃烧室结构段计算采用结构化网格，网格单元数4 800，网格节点数3 420，内部流场使用非结构化网格，网格单元数47 248，节点数为52 756。

1.2 双向耦合数值模拟流程

在本文的数值模拟过程中，结构温度场响应速度远低于流场温度变化速度，故将稳态温度结果作为固体域初始边界条件，计算中边界面采用绝热计算条件。本文通过ANSYS Workbench数据交换平台提供的System Coupling模块实现燃烧室结构段与内部流场的双向耦合[6]。燃烧室结构段变形分析采用ANSYS软件中的瞬态结构动力学分析方法，流场特性采用CFX中SST湍流模型进行分析。SST模型考虑了湍流剪切应力，避免了对涡流粘度的过度预测，广泛应用于流固耦合计算。本文在模拟声波传递过程中对燃烧室避免流动信息的捕捉要求较高，故采用SST模型。燃烧室与燃烧流场双向流固耦合求解采用双重循环迭代方法[7]。耦合计算流程如图2所示，将所处工况下的稳态温度场作为初始条件导入模型，根据给定的进出口压力对动量方程进行求解，确定流场中各节点的初始压力和速度，将过程的总时间分成若干个时间步，在每个时间步中做稳态计算。

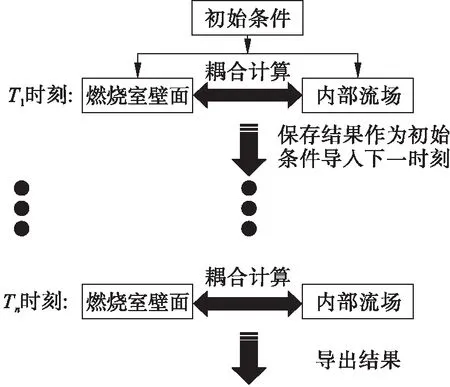
图2 计算流程图

单步耦合计算原理过程如图3所示。在某一时刻循环开始，以上一时刻流场压力p、速度v的分布和燃烧室结构段变形位移x作为初始条件进行计算，在流体域进行若干步计算收敛后，再通过网格插值将流场压力p、速度v的分布信息传递到流固耦合面。燃烧室固体耦合面以其为边界条件计算得到燃烧室结构瞬态动力响应，然后结构变形的位移x等信息再通过网格插值传递给流场耦合面作为流场耦合面的边界条件。当流体域与固体域的位移、载荷都达到收敛状态时，则完成一次双向耦合迭代计算，然后继续进入下一时刻循环。通过双向流固耦合计算，可获得任一时刻燃烧流场压力、速度及温度分布特性和燃烧室结构运动变形特性。

图3 单步耦合计算原理图

1.3 声压波模拟方法及验证

在燃烧室中，压力振荡的根源是燃烧的不稳定性，可将火焰视为声源。如果火焰在诸如管或燃烧室的密闭环境中燃烧，则产生的声波从边界反射。火焰对声波有很大影响，既可以削弱声波也可以进一步对声波进行放大。火焰放大某处声波的条件公式为

(1)

公式(1)表明，当声压振荡和放热振荡之间的相移小于90°时，相关的反馈机构产生声能，反之，声波被削弱[8]。因此，当评估燃烧的不稳定性时，关于燃烧室中声场的火焰相位行为的信息是非常重要的。在实际情况下，声能在入口、出口，通过壁面的振动和边界层中被吸收。这意味着关于火焰振幅特性的信息也很重要。当能量的产生大于耗散时，在每个振荡周期期间，系统中声能被增强，并且由于非线性效应，压力振幅增加直到饱和。当声压振荡和放热振荡之间的相移小于90°时，相关的反馈机构产生声能 。燃烧噪声可由波动方程来表达[9]

(2)

其中，t是时间，p是声压，ρ是平均流量密度，c是声速，γ是比热比，Q′为单位质量工资的热释放量。对于具有刚性壁的长棱柱管，声波传播方程可简化到一维形式

p(x,t)=A1ej(ωt-kx)+A2ej(ωt-kx)

(3)

设波沿x方向传播如图4所示，声压表示为p(x,t),

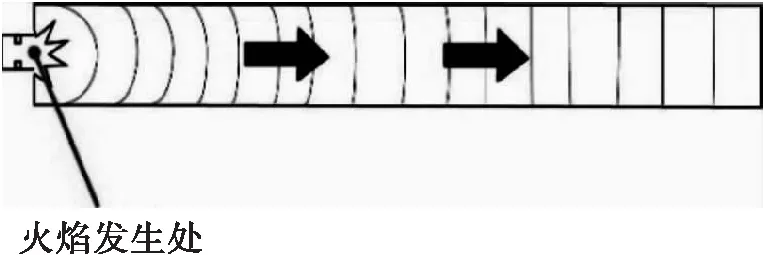
图4 声波传播示意图

(4)

波动方程为

(5)

将声波传播方程简化为一维形式

p(x,t)=A1ej(ωt-kx)+A2ej(ωt-kx)

(6)

其中A1和A2分别是在正负x方向上以平均声速c0行进的声压波的振幅，假设不存在反射波，则A2=0。k为角频率和声速之比，即k=ω/c0=2π/λ。再设x=0处的声源振动时，在毗邻介质中产生pmejωt的声压,则声压的振幅值pm，声场中的声压为p=pmej(ωt-kx)。

本文将由燃烧不稳定产生的压力波动视做声压波动，通过压力波与燃烧室壁面进行互相作用实现燃烧室内部流场与结构的双向耦合计算。应用CFD软件模拟声波传递过程，在燃烧室流场入口处施加正弦压力波动激励，设置流场中流体域为理想空气。模拟结果与通过公式计算得到理论结果对比，如图5所示。

由图5可知，火焰波前缘声波传递规律符合理论计算结果，不同位置的声波运动曲线的计算结果均与理论计算结果相符，说明所选择的网格密度及单步计算时间符合声波传递计算需要，此外也证明采用CFD技术分析声波传递是可行的。

图5 声波传递理论结果与模拟结果

1.4 双向耦合计算边界条件

图6给出了双向耦合建模的边界条件示意图。本文对燃烧室的燃烧过程进行模拟，各计算参数如表1所示。模型流体域入口均采用速度入口，燃料为甲烷[10]。模型流体域入口均采用速度入口，为了模拟持续的声压波动过程，将燃气入口分别设置为不同频率的脉冲入口[11]。

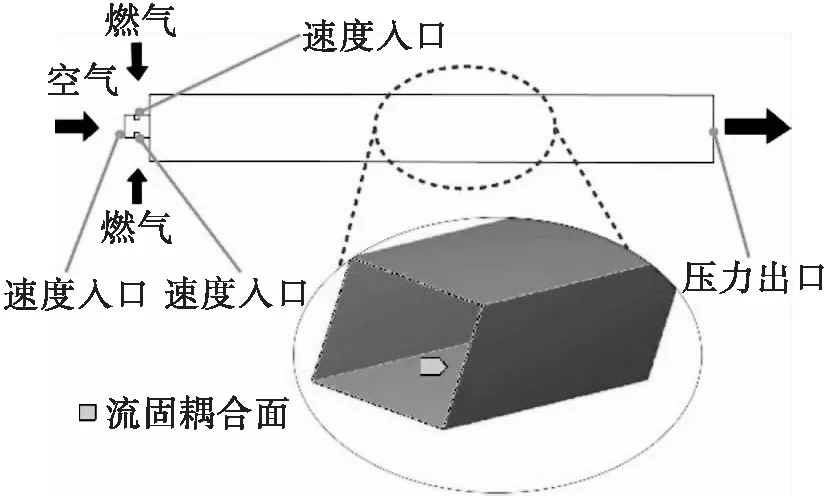
图6 边界条件示意图

状态参数数据进口空气速度20 m/s进口燃气速度100 m/s进口空气温度300 K进口燃气温度300 K出口相对压力0 Pa

出口采用压力出口，相对压力为0。湍流模型采用SST模型。燃烧室壁面与内部流场耦合面如图6中标签处所示，流体域耦合面为与固体域耦合面接触的对应表面。耦合面在瞬态多场求解器中设置为可移动边界条件。为了便于计算收敛，非定常求解计算以定常结果作为初始值。

2 模拟结果及分析

2.1 声压模拟结果

取55 Hz工况下不同时刻下燃烧室内压力分布云图如图7所示。图7显示了声波产生及传播的过程，传递方式可近似为平面波。本文中，假定燃烧室中声波质点不进行传播，故为驻波。

图7 不同时刻声压云图

取燃烧室中轴线上的点进行压力分析，燃烧室内各处声压幅值在燃烧室内不同位置变化情况如图8所示。

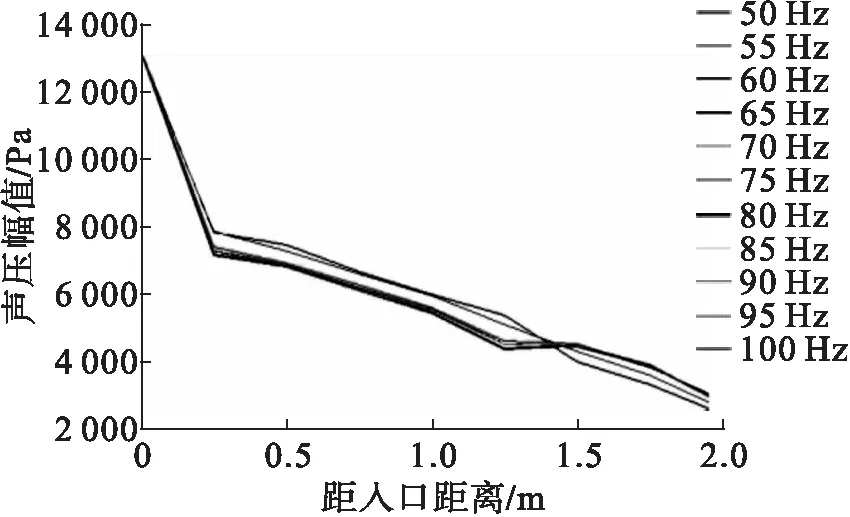
图8 燃烧室内各处声压幅值对比图

由图8可知声压在入口处具有较大幅值，到出口端声压幅值逐步减少，结合声压增强公式分析其原因是入口处的声压振荡与火焰放热振荡相位差较小，声波得到加强。远离入口时，声压振荡与放热振荡的相位差逐渐增大，声波增强效果减弱[12]。此外，燃烧室内声压变化还与燃烧室形状有关。

不同工况下的同一位置，声压幅值相差5%以内。燃烧室前半段声压力在模拟工况范围内，随频率升高而降低，后半段声压力随频率升高而升高。

2.2 燃烧室温度场模拟结果

取55 Hz工况下的不同时刻流场温度云图如图9所示。

图9 不同时刻温度场云图

由图9可知燃烧室内温度在前半段燃烧区变化较大，在后半段分布较为平均，取耦合区平均温度进行比较，如图10所示。

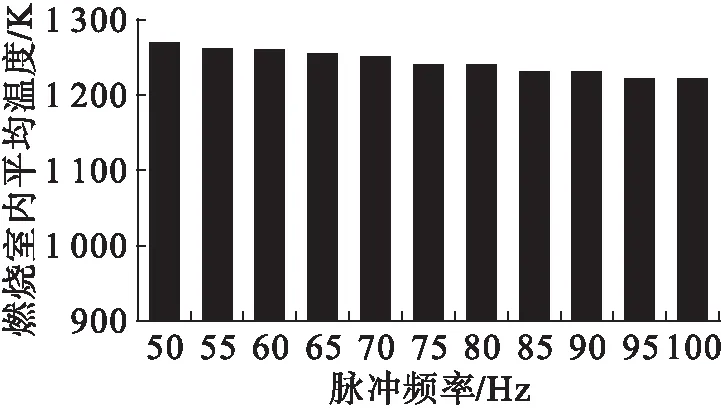
图10 不同工况燃烧室温度

结果显示改变燃烧脉冲的频率对燃烧室耦合段的温度影响较小,平均温度变化幅度在4%以下。

2.3 结构应力模拟结果

取不同工况下，燃烧室结构热应力随时间变化曲线如图11所示。

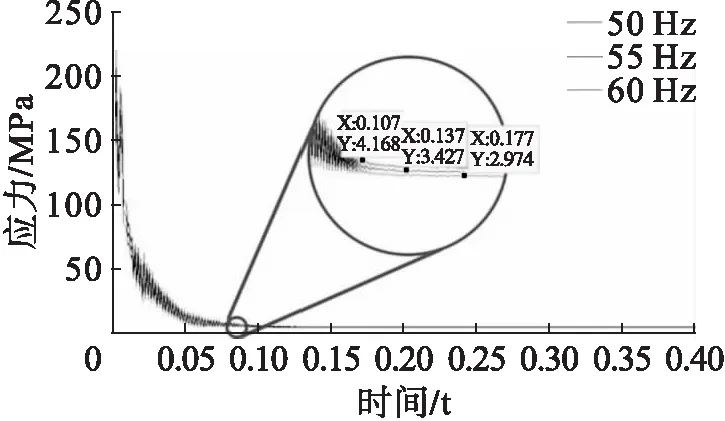
图11 不同工况下热应力随时间变化图

热应力随时间变化趋势一致，改变燃气脉冲频率使热应力略微降低，与温度变化规律一致。取55 Hz工况模拟结果进行分析，热应力分布云图随时间变化如图12所示。

对比图12和图13可知，高热应力区域与声压应力较高的区域有所重叠，在壁面拐角处应力较大，这些区域产生的局部应力集中现象，会导致疲劳裂纹的萌生和扩展，危及航空发动机和燃气轮机的安全运行[13-15]。取拐角处一点在不同工况下的应力图如图14所示。

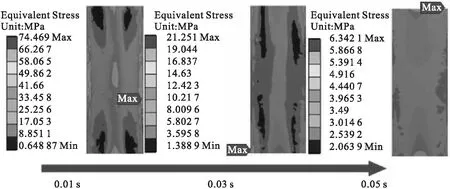
图12 不同时刻热应力云图

取55 Hz工况下结构段不同时刻下的应力分布云图如图13所示。

图13 不同时刻声压应力云图

由图14可知，各工况下声压应力的频率与入口条件所给定脉冲频率基本一致，声压应力的幅值变化呈现出与温度及热应力不同的变化规律，其中55 Hz声压激励下的结构响应明显大于其他工况。将每种工况应力曲线进行傅里叶变换得到频域图如图15所示。

由图15可知，各工况下应力大小不同且应力波主要与声压的前五倍频相关，其中一倍频对应力的影响最大。改变初始条件，计算多种工况下的平均应力情况如图16所示。

图16中频率值58 Hz及95 Hz对应的线代表计算所得燃烧室结构单元工作情况下单向耦合模态的频率；频率值51 Hz及80 Hz对应的线代表结构段固有频率。由图16可知，结构段应力的大小与其工作状况下的耦合模态有关，且可据此推断在双向耦合计算中，结构段耦合模态频率范围。

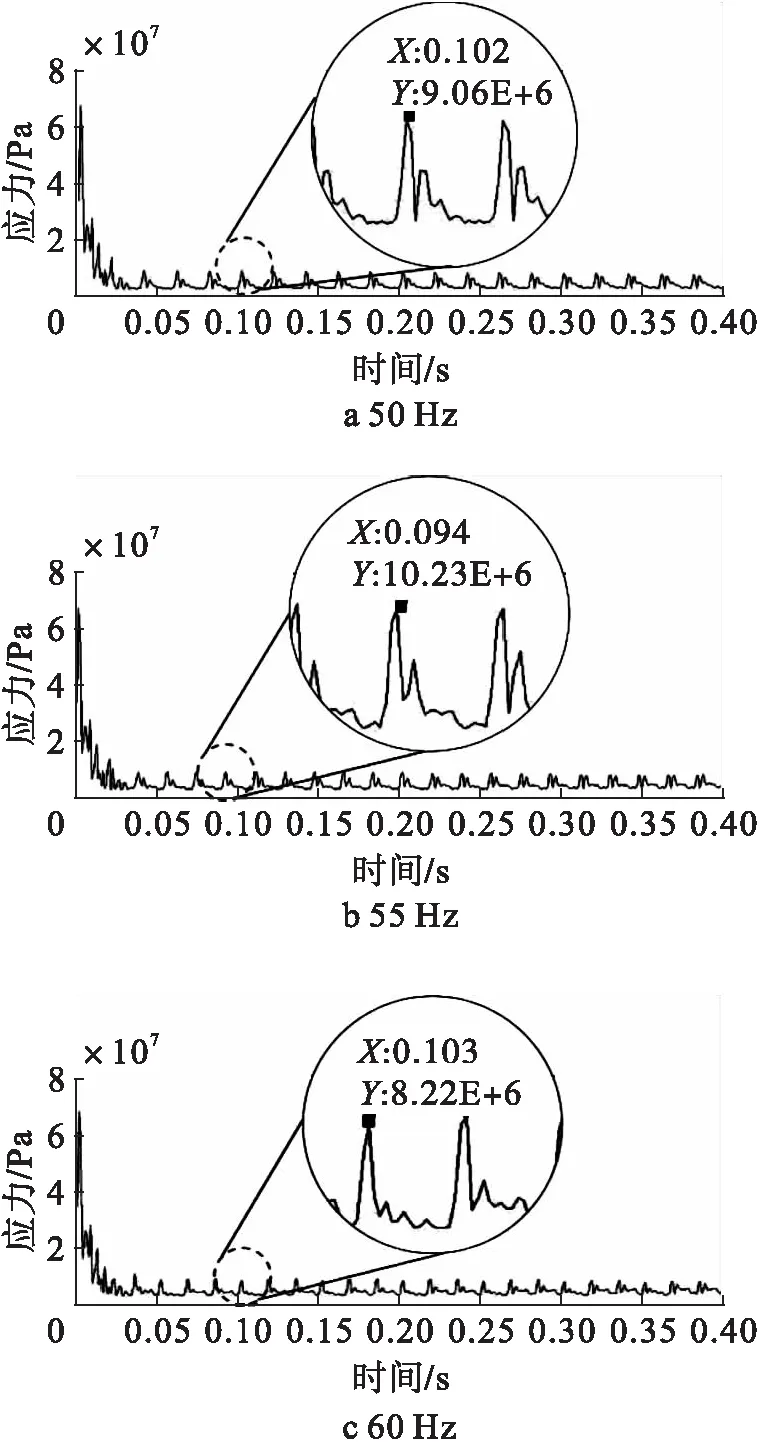
图14 50 Hz、55 Hz、60 Hz工况下声压应力随时间变化图

图15 50 Hz、55 Hz、60 Hz工况下声压应力随时间变化图

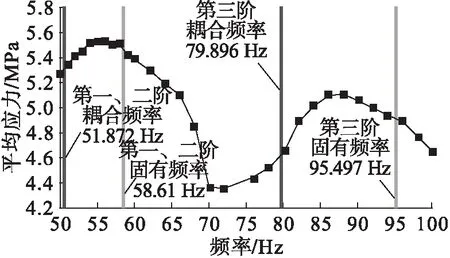
图16 不同频率声压作用下燃烧室响应结果

3 结论

本文得到如下结论：

(1)本文用CFX软件模拟声波传递的过程，计算结果与理论分析结果吻合较好，为双向耦合过程中声波传递特性模拟提供了一种有效的方法；

(2)受热声耦合作用影响，燃烧室内部不同位置声压分布不均，靠近出口处声压幅值显著降低，下降幅度约75%；

(3)燃烧室受热应力与声压应力共同作用，热应力与声压应力量级相同，两者对结构的影响皆不可忽略，且声压应力为交变应力，易引起结构共振；

(4)燃烧室结构对声压的响应与声压激励频率有关，当激励频率与燃烧室结构固有频率接近时，声压应力会有显著提高。