一种用于偏心孔损伤容限测试的轮盘设计

陈国栋，刘 闯，王洪斌，张昕东，刘正峰

(中国航发沈阳发动机研究所 辽宁省航空发动机冲击动力学重点实验室，沈阳 110015)

设计损伤容限测试用轮盘，能够为发展裂纹在线监测技术提供真实的测试及验证环境。国外航空发动机公司及研究机构非常重视轮盘疲劳裂纹的在线监测技术，通过监测、分析振动信号开展研究工作，已进入应用阶段[1-5]。美国的Allison Advancrd Development company(AADC)、Creative Engineering Concepts Inc.(CECI)、General Electric Company(GE)、Test Devices Inc.(TDI)等均有其先进的在线故障诊断技术[6]。目前，国内应用振动监测及声发射技术开展了针对旋转机械的裂纹在线故障诊断方法的研究，翟鹏程等[7]通过改变转子裂纹深度、质量不平衡方向研究转子的振动变化，研究结果对转子裂纹的识别和监测具有指导意义；武红霞等[8]对裂纹转子的非线性输出频域响应函数进行了仿真分析和试验验证，拓展了转子裂纹在线监测的理论基础；毛汉领等[9]通过安装在转子上的声发射传感器进行信号采集、分析，实现了对水轮机转轮的裂纹在线监测；薛凯璇[10]利用声发射技术对故障轴承进行信号提取与分析，提出了一种基于粗糙集与神经网络结合的故障诊断方法。以上裂纹在线监测技术仍停留在理论研究及测试阶段，缺乏针对实际轮盘的有效性试验验证，当前进行裂纹扩展试验的真实发动机轮盘数量较少，因此有必要设计损伤容限测试用轮盘进行裂纹在线监测技术的研究。

开展模拟局部真实损伤容限结构的轮盘设计与试验，能够以较低的成本代价为损伤容限设计与分析提供数据支撑。在损伤容限设计方面，国外开展了大量真实发动机轮盘关键部位的裂纹扩展试验，逐步提升了裂纹扩展寿命的预测精度，Hou等[11]通过在轮盘上预制缺口的方法进行整盘的裂纹扩展试验，通过外观及解剖检查获得了裂纹扩展速率，并研究了数值仿真分析方法；Beres等[12]应用Zencrack、Abaqus软件预测轮盘榫槽底部裂纹扩展速率，并与真实轮盘的试验结果进行对比分析，验证了预测方法的准确性；Farukh等[13]通过粘塑性本构模型预测了镍基合金的裂纹扩展速率，与试验结果的符合性较好。国内，魏大盛等[14]采用J积分方法对粉末冶金拉伸试样的裂纹扩展寿命进行仿真分析，计算结果与试验结果吻合较好，并对涡轮盘进行裂纹扩展寿命分析；秦银雷等[15]采用2自由度数值方法描述裂纹前沿形状的发展，对涡轮盘裂纹扩展进行仿真分析；白杰等[16]针对损伤容限适航要求对涡轮盘偏心孔部位的损伤容限评估流程开展研究及验证，为适航审定技术研究提供支持。目前国内的损伤容限设计和分析方法仍不成熟，缺乏真实轮盘各部位的裂纹扩展试验验证，因此有必要快速积累轮盘裂纹扩展速率的试验数据。

1 损伤容限测试用轮盘的设计要求

对于发动机轮盘，损伤容限测试位置一般为裂纹萌生寿命较短的部位或一旦发生断裂会造成危险性影响的关键部位。其中偏心孔结构由于存在明显的应力集中及应力梯度，一般具有较长的裂纹扩展寿命，是损伤容限设计与分析的主要对象。

依据真实发动机轮盘的偏心孔结构特点，同时考虑到运行周期与成本，设计要求如下：

(1)测试位置应力水平较高，裂纹萌生寿命较短，裂纹萌生寿命目标8000次循环；

(2)应力梯度明显，有一定的裂纹扩展寿命，工程裂纹到临界裂纹尺寸的裂纹扩展寿命不低于100次循环；

(3)测试位置以外的轮盘其它位置应力水平较低；

(4)失效后的能量较低，一旦破坏后对设备损伤小；

(5)便于目视及无损检测。

2 轮盘设计

2.1 失效能量影响分析及转速选取

为保证盘辐区域的名义应力水平最高，需将测试盘设计为空心盘。以等厚空心轮盘为例，总失效能量可以用式(1)表示，式(1)中m为轮盘质量，ro为轮盘外径，ri为轮盘内径，ρ为材料密度，ω为角速度，b为轮盘厚度。当指定轮盘厚度及材料时，总失效能量与轮盘外径、内径尺寸及转速有关，这3个参数也直接影响空心盘的应力水平，等厚空心盘的周向应力及径向应力计算公式分别如式(2)、(3)所示，式中υ为材料泊松比，r为应力计算位置的半径。

(1)

(2)

(3)

盘心内径过小会导致内孔应力集中，考虑设备驱动轴组件安装边的尺寸，将内孔直径确定为0.04 m。依据公式(1)、(2)、(3)，在内孔直径确定,盘辐应力维持不变的情况下，为使转动动能更低，需提高转速。考虑到设备运行能力，转子转速确定为16 000～18 000 rpm，在此基础上设计轮盘外径。

2.2 材料选取

在相同外载的条件下，为了保证一定的裂纹扩展寿命，应选取裂纹扩展速率较低的材料。在所有裂纹扩展的因素中，弹性模量E、扩展门槛值△Kth和断裂韧性KC是裂纹扩展阻力三要素，会直接导致裂纹扩展行为的变化,而其它因素对裂纹扩展的影响是间接的[17]。对于同一类金属弹性模量E差别不大，扩展门槛值△Kth与断裂韧性KC同断裂强度σf和断裂韧性εf正相关。另外，尽量选取真实发动机轮盘用材料，为损伤容限分析提供有效数据支撑。考虑到裂纹扩展速率、材料代表性及加工成本，最终选取1Cr11Ni2W2MoV钢锻件加工测试用轮盘。

2.3 损伤容限测试位置应力水平设计

根据8 000次循环寿命的设计目标，分别使用名义应力法及局部应力-应变法进行已知循环寿命的损伤容限测试位置应力水平反算。

2.3.1 名义应力法

名义应力法是通过材料S-N曲线得到指定应力水平和循环特征下的疲劳极限。一般S-N曲线为应力比为-1的应力寿命曲线，而轮盘载荷为非对称循环，需要考虑平均应力对疲劳寿命的影响，工程上常用Gerber、Goodman及Soderberg图进行平均应力修正[18]。使用如图1所示的S-N曲线与Goodman图组合估算法，进行指定名义应力下的寿命计算，首先计算出该名义应力下的平均应力和应力幅，平均应力作为Goodman图中A点的横坐标，将应力幅乘以有效应力集中系数Kf作为Goodman图中A点的纵坐标，之后通过等损伤线由A点确定应力比为-1的B点，将B点沿水平投影至S-N曲线上，得出该应力水平对应的循环数。通过迭代，可以得出指定循环寿命对应的名义应力。

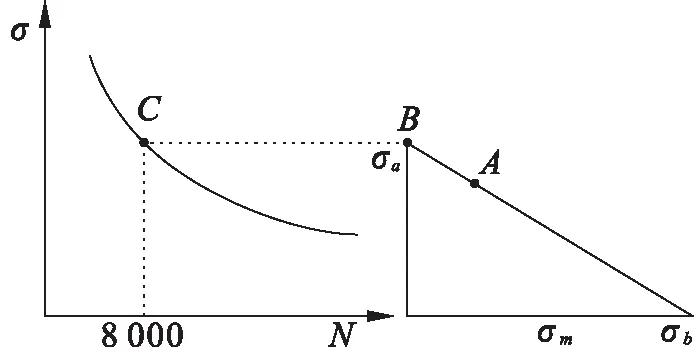
图1 S-N曲线与Goodman图组合估算寿命法

依据参考文献[19]中给出1Cr11Ni2W2MoV轴颈钢锻件室温条件下应力比为-1的S-N曲线，疲劳极限为664 MPa。应力为772 MPa时对应的寿命为100 000次，应力为830 MPa时对应的寿命为40 000次，曲线中最短寿命大于30 000次循环，有效应力集中系数Kf经计算取1.4。

为便于计算，将S-N曲线进行对数转化，通过相似三角形得出8 000次循环寿命对应的C点应力为835 MPa。

2.3.2 局部应力应变法

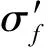
(4)

(5)

已知局部名义应力计算寿命时，将Δεt带入Manson-Coffin公式便可求解出寿命Nf。已知循环寿命，使用局部应力-应变法计算应力水平时，先将寿命带入应变寿命公式，得出应变变化范围,之后将应变变化范围带入应力应变公式，得出应力变化范围,最后通过Topper公式[22]得出损伤容限测试位置的局部名义应力，Topper公式如式(6)所示，式中△S为名义应力，△e为名义应变。

(6)

轮盘材料选取1Cr11Ni2W2MoV，低周疲劳性能数据参见参考文献[23]。

采用Manson-Coffin公式存在一定缺陷，未考虑平均应力不为零时的情况。考虑平均应力对应变寿命预测，多个针对Manson-Coffin公式的修正模型被提出[20]。使用多种方法计算指定8000次循环寿命下的局部名义应力范围ΔS，计算结果对比见表1所示。

表1 8 000次循环寿命下的局部名义应力△S计算结果对比

根据计算结果，使用Manson-Coffin公式、通用斜率法计算的局部名义应力结果接近或超过材料的σb，局部名义应力计算值偏高，主要是因为针对0～σmax的轮盘循环载荷特征，这两种算法未考虑平均应力不为零的影响。Endogan-Roberts修正公式、改进的SWT参数模型虽然考虑了平均应力不为零的影响，但由于无法准确获得计算所需的全部材料性能参数，导致局部名义应力计算结果超过σb。Morrow修正公式、Manson-Halford修正公式及SWT参数模型考虑了平均应力的影响，且能够获得计算所需的材料性能参数，因此具有更好的修正结果。最终选取与名义应力法接近的Morrow修正公式的计算结果，损伤容限测试位置的名义应力设计为810 MPa。

2.4 结构设计

优先选取与名义应力法接近并且应力水平较低的Morrow修正公式的计算结果进行结构设计，保证损伤容限测试位置的名义应力为810 MPa。

使用有限元分析软件Ansys进行计算，为降低转角处应力，对部分转角作圆弧设计，最终的有限元模型见图2，偏心孔数量为12个。转速取16 356 rpm时，三维线弹性计算结果显示偏心孔3、9点钟位置的最大径向应力为810 MPa。

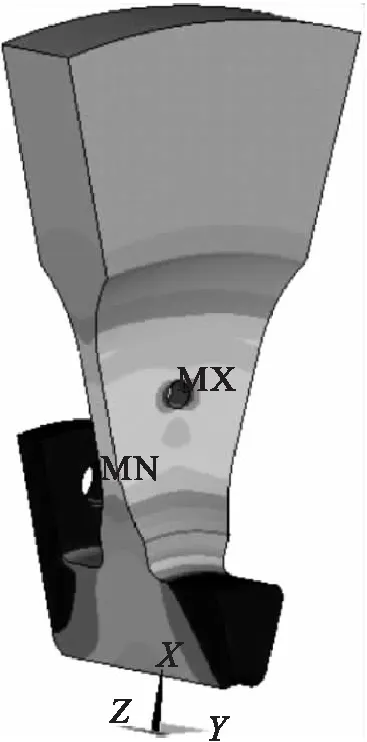
图2 有限元模型

3 强度储备分析

由轮盘结构可知，经过偏心孔6点钟和12点钟位置的子午面平均周向应力最大，经过偏心孔3、9点钟位置的辐板周向截面平均径向应力最大，对轮盘应力进行线弹性分析，以上2个截面的平均应力云图见图3和图4所示，平均应力计算结果和储备分析见表2所示，可见2个危险截面的强度储备系数均大于1.0，轮盘在试验转速下不会发生破裂。对轮盘进行弹塑性分析，偏心孔当量塑性应变计算结果如图3所示。偏心孔3、9点钟位置当量塑性应变最大，最大当量塑性应变为0.53%，文献[19]给出的最小延伸率δ5为6%，远大于计算得出的最大当量塑性应变，塑性应变分析结果显示轮盘在试验转速下不会发生破裂。

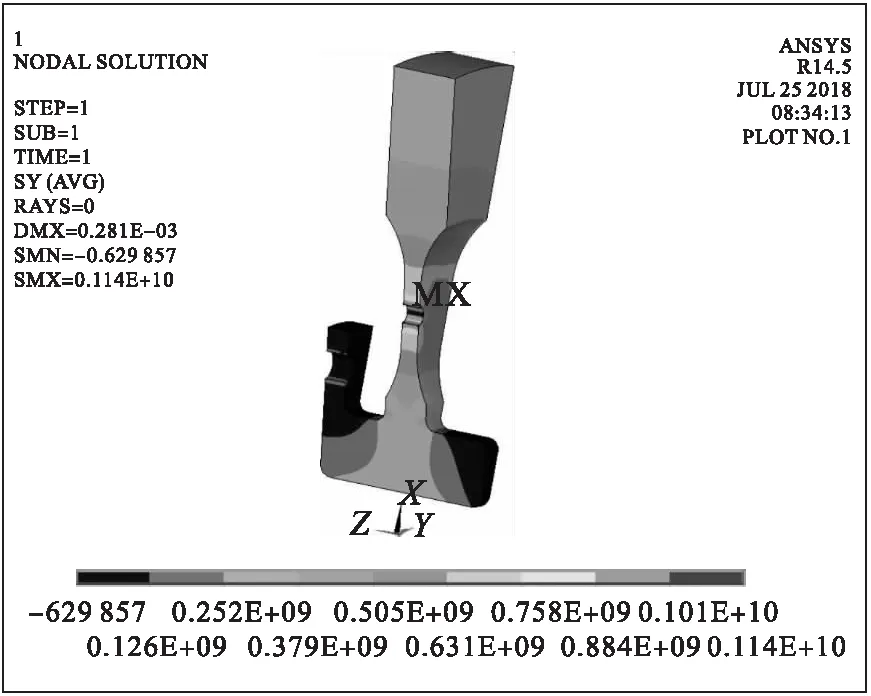
图3 经过偏心孔6点钟和12点钟位置的子午面平均周向应力云图

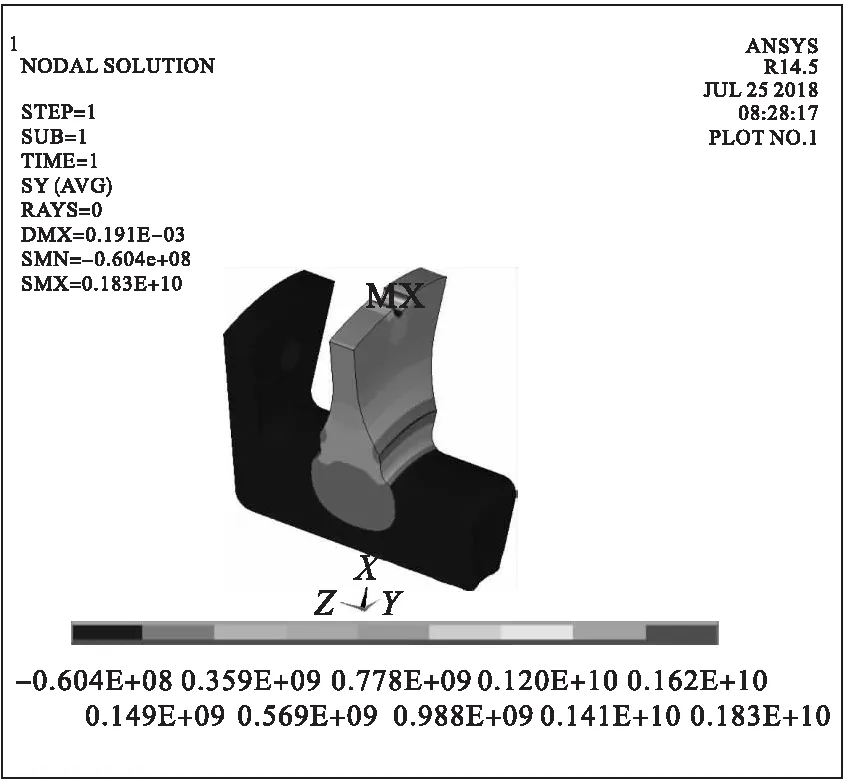
图4 经过偏心孔3、9点钟位置的辐板截面径向应力云图

表2 平均应力计算结果和储备分析

4 损伤容限分析

4.1 Paris公式

疲劳裂纹扩展速率用da/dN表示，它是裂纹尖端应力强度因子范围ΔK的函数(其中a为裂纹长度，N为循环次数)。Paris公式[24]如式(7)所示，式中C、n为常数，ΔK为应力强度因子范围，可由式(8)计算，式(8)中α是与试件及裂纹几何形状有关的系数，对于有限宽度的平板单边裂纹，可由式(9)计算[25]，式(9)中a为裂纹深度，w为平板宽度，b为裂纹深度除外的剩余宽度。式(7)转换为式(10)后，可进行积分计算得出裂纹扩展寿命，如式(11)所示，式(11)中a0为初始裂纹尺寸，取0.76 mm，ac为临界裂纹尺寸。

(7)

(8)

(9)

(10)

(11)

大量试验结果表明，n与C之间可由式(12)表示[26]，B约为1/55，A在普通钢中约为1/20000，对于各种金属n大约为2～7，这里n取2。计算C值为1.65×10-9。

C=ABn

(12)

临界裂纹尺寸ac可由材料断裂韧度求得，如式(13)所示[27]，KIC取145MPam0.5[19]。计算临界裂纹尺寸ac值为3.9 mm。通过式(11)计算得出裂纹扩展寿命为175次循环。

(13)

4.2 其他裂纹扩展模型

关于疲劳裂纹亚临街扩展的理论模型较成熟有三类，分别为塑性钝化模型、极限值模型及再成核模型。考虑到可获得的材料性能参数，采用塑性钝化模型中的Lardner R.W公式进行计算[26]。Lardner R.W公式如式(14)所示，式中μ为剪切弹性模量，υ为泊松比，σb为拉伸强度极限。使用Lardner R.W公式计算的裂纹扩展寿命为164次。

(14)

5 结论

依据损伤容限测试的特点与需求，设计了损伤容限测试位置的应力水平及轮盘的整体结构，得到如下主要结论：

(1)针对偏心孔作为损伤容限测试位置的轮盘，为保持较低的轮盘失效后能量，应该依据试验设备优先考虑内孔尺寸及试验转速，在此基础上开展其他设计。

(2)指定寿命下的应力计算结果表明Morrow修正公式的计算结果与名义应力法计算结果更加接近，由此设计的轮盘经线弹性及塑性应变分析，结果显示强度储备满足测试要求。

(3)由于缺乏有效试验数据支持的参量，裂纹扩展寿命未进行深入计算分析，但保守的计算结果表明，裂纹扩展寿命高于100次循环。在实际试验中，发现萌生裂纹后，可通过缩短检查周期或降低转速的方式，有效监测裂纹扩展的速率。