基于有限元仿真的弹性环刚度特性分析

刘 闯，陈国栋，杨 阳，侯小捷，罗 忠，张昕东

(1.中国航发沈阳发动机研究所 辽宁省航空发动机冲击动力学重点实验室，沈阳 110015；2.东北大学 a.机械工程与自动化学院，沈阳 110819；b.航空动力装备振动及控制教育部重点实验室，沈阳 110819)

弹性环作为现代航空发动机中的一种重要的弹性支承结构，是一种内外表面都有相互交错且均匀分布若干凸台的环形弹性元件，对于调整发动机临界转速，保证工作转速下具有足够的安全裕度有着十分重要的作用[1-4]。进行弹性环结构设计时，通过调整其几何参数即改变支承刚度，从而达到在不改变相邻结构的情况下控制转子系统临界转速的目的[5-7]，具有结构简单，调整方便的特点。在发动机结构中，弹性环内表面凸台一般支承于轴承外环，外表面凸台一般支承于机匣或支座的内壁(外支承环)，如图1所示[8]。

图1 航空发动机弹性环安装结构图

研究弹性支承刚度设计方法及其刚度的敏感影响因素，对于航空发动机设计有着十分重要的作用[9-13]。目前，许多学者对于弹性环的刚度设计方法进行了相关研究。曹磊[14]等把理论解析方法和有限元仿真方法进行对比，提出有限元方法能够在充分考虑多种结构参数的条件下更加精确地计算弹性环刚度；刘勇[15]等基于有限元仿真软件分析等效刚度随不同结构参数的变化规律，给出了综合考虑加工、安装、稳定性因素的优化设计方案。龙向阳[16]等通过有限元仿真的方法研究了弹性环刚度仿真计算的准确性和结构参数变化对弹性环刚度特性的影响，定性地给出了不同参数对弹性环刚度大小的影响程度。

本文分别采用理论计算和有限元方法对某型弹性环结构的刚度特性进行了分析，验证了分析方法的有效性。采用有限元法分析了弹性环刚度对不同结构参数的敏感性，对发动机中弹性环支承结构设计具有一定的参考价值。

1 弹性环刚度理论计算

1.1 弹性环参数

本文研究的弹性环结构形式如图2所示，其中，D为内凸台表面直径，Δ为凸台高度，s为壁厚，b为凸台长度，r为凸台根部倒圆半径，L为弹性环宽度。

图2 弹性环结构示意图

1.2 理论计算方法

弹性环结构具有环段数量多，跨度小，环厚度远小于环半径的特点，因此计算时将每一段环简化为两端固支的直梁分析，同时采用材料力学方法推导出其刚度计算公式[17-19]。

在计算时，每个弹性环可以分成m个环段，在径向载荷作用下仅半部分弹性环承受载荷，其中只有(m/2-1)个环受力作用，如在承受向下径向载荷时弹性环结构受力情况如图3所示。

图3 弹性环受力图

每个环段支承力为F0、F1、…、Fi，则轴承总的作用力F可以表示为

(1)

式(1)中，α=2π/m。

两端固支的等截面梁中央截面处的柔度δ为

(2)

其中L为环段长，I为环段截面惯性矩，E为环段材料的弹性模量。

则环段整体柔度δt为

(3)

最终弹性环整体刚度由K=1/δt得到。

但是上述理论公式不足之处在于理论计算时将环段近似看作等截面直梁，这样简化忽略了凸台高度以及圆角半径等结构参数对整体刚度的影响，导致计算结果存在一定偏差。相反有限元法不仅精度高而且可以考虑更多的几何特征，因此本文基于有限元法对弹性环的刚度特性进行分析，并分析弹性环刚度对各个结构参数的敏感性及其变化规律。

2 弹性环有限元模型建立

2.1 模型建立

采用ANSYS有限元软件对弹性环组件进行建模。某型弹性环的相关参数如表1所示。为保证模型计算收敛性、减小计算量以及确保模型载荷真实，考虑到弹性环受力变形具有对称性，取1/2模型进行计算分析。最后建立的有限元分析模型如图4所示。其中1为弹性环；2、3分别为弹性环内、外衬套；4、5分别模拟轴承外环和轴承座。

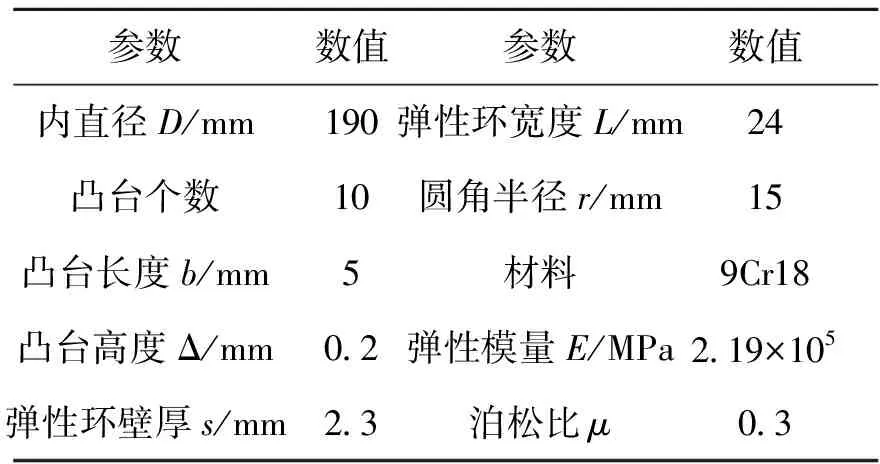
表1 弹性环参数

图4 有限元分析模型

2.2 边界条件设置及网格划分

约束轴承座外圈所有节点的x、y方向自由度，同时约束二分之一模型纵向对称线处所有节点的x方向自由度，并且在轴承外环内圈施加竖直向下的载荷力。为使仿真结果更具可靠性，利用TARGE169单元和CONTA172单元建立接触对，模拟弹性环内、外凸台与衬套之间以及内外衬套与轴承外环和轴承座之间的接触状态，使用PLANE82单元对弹性环组件进行分网，有限元网格模型如图5所示。

图5 有限元网格模型

2.3 弹性环仿真刚度计算

在刚度分析过程中，设定轴承外环所受径向载荷为F，通过仿真结果得到模型各部分沿载荷方向的变形情况如图6所示。

图6 弹性环变形情况

分别提取内衬套外表面(图7中a面)的平均位移和外衬套内表面(图7中b面)节点的平均位移，将两者位移差作为F载荷作用下弹性环的位移变形量，将载荷与此变形量之比确定为弹性环刚度。

图7 位移提取示意图

根据多次仿真结果结算得到不同载荷作用下弹性环位移，载荷与位移关系如图8所示，通过线性拟合得到此结构参数下弹性环的刚度为1.27×107N/m。

图8 刚度分析结果散点图

而通过理论公式(3)计算得到的理论刚度值为1.15×107N/m，理论结果与仿真结果大致相当。同时由于有限元仿真考虑因素更为全面，因此认为有限元分析结果更贴近真实刚度值。

3 刚度敏感性分析

为了确定弹性环的敏感参数，分别改变表1中的壁厚s、凸台高Δ、圆角半径r、弹性环宽度L，分析其对弹性环刚度的影响规律。

3.1 壁厚影响分析

为弹性环壁厚对刚度的影响规律如图9所示。由图9可以看出，弹性环刚度随壁厚增大而增大。

图9 刚度随壁厚变化趋势

3.2 圆角半径影响分析

弹性环圆角半径对刚度的影响规律如图10所示。由图10可以看出，弹性环刚度随圆角半径增大而增大，但相比其他量的影响变化幅度很小。

图10 刚度随圆角半径变化趋势

3.3 凸台高度影响分析

弹性环凸台高度对刚度的影响规律如图11所示。由图11可以看出，弹性环刚度随凸台高度增大而增大。

图11 刚度随凸台高变化趋势

3.4 凸台长度影响分析

弹性环凸台长度对刚度的影响规律如图12所示。由图12可以看出，弹性环刚度随凸台长度增大而增大。

图12 刚度随凸台长度变化趋势

3.5 敏感性分析

不同结构参数对弹性环刚度的影响程度不同，为了在设计时能够了解弹性环刚度对不同参数的敏感性，将各个参数对刚度影响进行了对比，如图13所示。

图13 各参数影响对比

采用差分法计算各个参数的灵敏度系数，为了便于对不同参数的灵敏度系数进行比较，对不同参数的灵敏度进行了无量纲处理，再进行均化处理，结果见表2所示。

表2 各参数灵敏度系数

由表2可知，壁厚对弹性环刚度影响最大，之后分别是凸台长度与凸台高度，圆角半径几乎没有影响。其中圆角的作用主要是改善弹性环凸台结构处的应力集中，降低截面变化处的应力水平，对于刚度的影响很小，无法实现调节刚度的作用；而凸台长度和高度的变化并未对弹性变形段结构带来显著地影响，仅可用于对刚度设计值的微调；壁厚参数的变化则直接改变了弹性环的截面惯性矩，根据材料力学理论可知，截面惯性矩是影响结构抗弯能力的重要参数，对弹性环刚性影响很大，因此在进行弹性环刚度设计时需将壁厚作为最主要因素进行考虑。

4 结论

(1)采用有限元法对某型弹性环支承组件的刚度进行了分析，通过与理论分析进行对比发现，有限元方法能够有效地分析弹性环结构的刚度特性，数值仿真结果与理论分析具有较好的一致性。

(2)基于建立的参数化有限元模型，分析不同结构参数对弹性环支承刚度的影响。结果表明，弹性环结构刚度随着壁厚、凸台高度、凸台长度以及圆角半径的增加而增大，但增大的幅度不同。通过对比各个参数的灵敏度系数可知弹性环支承刚度受壁厚影响最大，凸台参数次之，圆角半径几乎没有影响。