功能梯度材料的低温挤压成形过程建模与实验研究

马维东 李淑娟 杨磊鹏 王馨翊 谷中豪

西安理工大学机械与精密仪器工程学院，西安，710048

0 引言

功能梯度材料(functionally gradient material，FGM)又称梯度材料，是基于新的材料设计理念而研发制备出的一种新型功能材料。它是指材料的化学构成、微观结构和原子排列由一侧向另一侧呈连续梯度变化，从而使材料的性质和功能也连续地呈梯度变化[1]。目前，制备FGM的方法有离子喷涂法、电沉积法、激光熔覆法、气相沉淀法等[2]。这些方法都采用高温下的复杂模具成形，工艺过程复杂，生产成本高。

本文采用低温和常温挤压自由成形[3]零件然后进行高温烧结的方法制备功能梯度材料,该方法采用无模自由成形，可以在低成本下实现复杂零件的成形。但是低温挤压自由成形过程中一般使用水基膏体，成形过程中会产生气泡和结块，结块的分解和气泡的结合及释放都会使成形过程处于不稳定状态，且水基膏体中水含量的多少，使其存在不同程度的液相迁移[4]现象，导致整个挤压成形过程难以控制。MASON等[5-6]设计了用于材料挤压过程的Bang-bang控制模型，通过力的反馈达到一定的控制效果，并指出膏体的黏度、层厚、挤出率和挤压速度均会对成形零件产生影响。BRYANT等[7]研究了快速低温成形过程中工艺参数对成形过程的影响。SUI等[8]采用低温挤压沉积技术制备了Al2O3/ZrO2梯度材料。MASON等[9]的研究表明，环境温度会直接影响陶瓷膏体的黏度，导致挤出效果变化显著，并且在低温下具有较高的定形能力。李淑娟等[10]采用低温沉积过程挤压力控制方法进行了三维陶瓷零件的制备。郑华滨[11]通过比较不同挤出工艺参数对挤压力和挤出体液相含量的影响,得到了较好的挤出工艺参数。焦盼德等[12]设计了自适应挤压控制器，一定程度上解决了系统不稳定问题。

本文在文献[10,12]所述陶瓷材料低温成形过程出现的问题的基础上，分析了FGM挤压沉积成形过程中，影响材料成形的各种因素，采用系统辨识的方法对挤压过程进行建模和辨识，设计并完善了最小方差自适应控制器，对功能梯度材料的挤压成形过程进行了实时控制，实验结果对比表明了该方法的有效性。

1 低温挤压自由成形技术

低温挤压自由成形(freeze-form extrusion fabrication，FEF)技术是一种基于水基膏体挤压、沉积、冷冻成形的快速成形技术[13]。该技术的成形材料以固体颗粒(如陶瓷颗粒)、水为主，加入少量的黏结剂、分散剂及润滑剂混合而成，利用低温环境中水结成冰使材料成形，在去除水、黏结剂的后处理过程中，冰变为水体积缩小，能有效减小成形件内部应力。该成形过程对环境污染小，符合当前倡导的绿色制造要求。

低温挤压自由成形技术和其他自由成形技术相似，成形原理如图1所示。

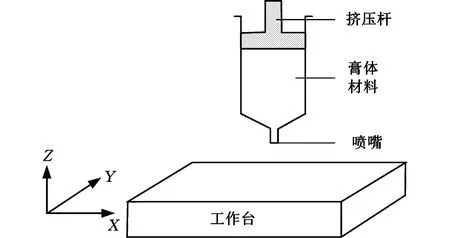
图1 低温挤压自由成形技术原理图Fig.1 Free extrusion technology schematic diagram

在低温挤压成形过程中，首先将制备好的触变性良好的材料膏体装入料筒里，膏体在挤压力的作用下从挤出头挤出，堆积在工作台表面。由于工作台表面的温度低于膏体的凝固温度，故挤出的膏体沉积在工作台上后立即固化。注射器沿着由CAD模型所生成的轮廓移动，在每一层堆积结束之后，Z轴移动一定的距离，该距离相当于每层切片的厚度。因此，通过控制挤出头在Z轴方向和XY平面的移动，经过二维切片的层层堆积最终即可形成所需的三维零件。为了使挤出体能更精确地堆积在既定的位置，挤出体的挤出速度与XY平面移动的速度应当相匹配[14]。

采用FEF技术搭建的FGM平台是在三坐标雕刻机上开发出来的新型增材制造装置[10]。FGM沉积成形系统的硬件系统利用一台现有三坐标雕刻机和由NI USB-6343 数据采集卡、松下A50伺服控制卡、伺服电动缸、测力传感器、储料器、混合器、PC机等组成的控制系统搭建而成。FGM 沉积成形控制系统结构如图2所示。

2 FGM材料挤压过程建模

FGM打印的水基膏体材料存在不同程度的液相迁移现象，气泡和结块对系统稳态也有很大的影响，这些因素对材料混合和成形精度有较大的影响。采用系统辨识的方法，根据实验过程中挤压缸的电压变化和挤出力的变化，对系统模型进行辨识、建模，并设计自适应控制器，实时控制材料挤压成形过程，最大程度地减小液相迁移、气泡、结块对系统带来的影响，可实现功能梯度材料的制备。

BOUCHONMEUNIER等[15]对系统辨识定义如下：“系统辨识是在输入和输出数据基础上，从一组给定的模型类中确定一个与所测系统等价的模型。”系统辨识中主要包含三个因素，即输入输出数据、模型类、等价准则[16]。其中，数据是系统辨识的基础，等价准则是优化目标，模型类是确定模型的范围。系统辨识的具体步骤如图3所示，首先通过实验获得系统的输入、输出数据(必须充分激励系统的所有模态)，然后利用系统的输入输出数据进行系统模型阶次辨识和参数辨识，最后对获得的系统模型进行验证，若符合要求则模型建立完成，若不符合要求则重新辨识，直到模型满足要求为止。

2.1 模型的阶次辨识与估计

2.1.1残差方差分析

考虑如下模型：

A(z-1)z(k)=B(z-1)u(k)+v(k)

(1)

(2)

式中,n为模型阶次；an和bn为系统模型的参数。

模型写成最小二乘格式为

(3)

其中，数据向量和参数向量定义为

运用最小二乘原理，可获得模型参数θn的最小二乘估计为

(4)

其中，数据矩阵和输出向量定义为

zn=(z(1),z(2),…,z(L))T

其中，L为数据长度。模型阶次为n时，输出残差向量可写成

(5)

(6)

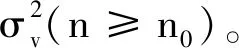
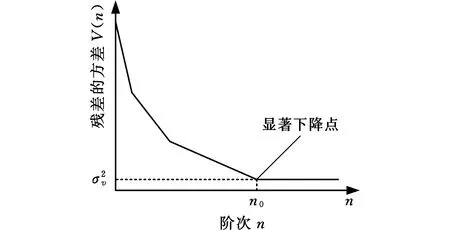
图4 模型阶次分析图Fig.4 Model order analysis chart

2.1.2模型阶次辨识

通过观察残差的方差V(n)的变化情况，可确定模型的阶次[13]。

给A、B缸(图2)分别输入0～5 V的逆M序列，采集挤压过程中的力信号，如图5所示。对A、B缸进行阶次辨识，编写MATLAB程序，辨识输入输出数据，得到的输入如表1所示。根据F检验法可知，A、B缸的模型阶次均为2，则A、B缸的挤压系统差分模型为

F(k)=a1F(k-1)+a2F(k-2)+b1U(k-1)+b2U(k-2)+v(k-2)

(7)

式中，F(k)为对应模型输出；U为模型输入；a、b为模型输入、输出参数；v为干扰噪声。

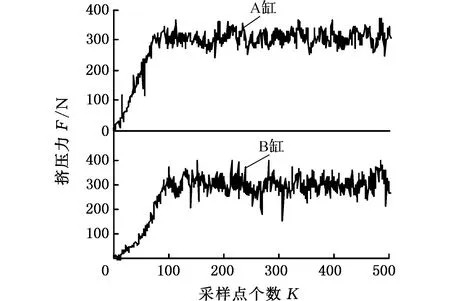
图5 挤压缸A、B的挤压力信号Fig.5 Squeeze force signal of squeeze cylinders表1 A、B缸的阶次分析Tab.1 A, B cylinder of the order analysis

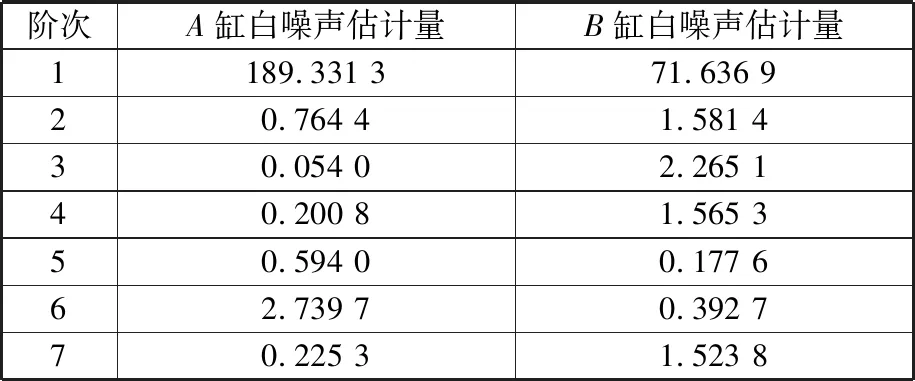
阶次A缸白噪声估计量B缸白噪声估计量1189.331 371.636 920.764 41.581 430.054 02.265 140.200 81.565 350.594 00.177 662.739 70.392 770.225 31.523 8

2.2 模型参数辨识

本文采用基于递推最小二乘(recursive least square,RLS)的最小方差自适应算法[17]对系统进行实时控制。根据输入输出数据在线实时估计系统参数，将参数辨识结果用于最小方差自适应控制。

为了便于进行数字采样，将式(7)进行离散化处理后写成差分方程形式：

F(k)=aF(k-1)+bU(k-1)

(8)

为了辨识式(8)中参数a和b，将式(8)改写为

F(k)=φT(k)·θ+n(k)k=1,2,…，n

(9)

式中，F(k)为过程输出量；φT(k)为可观测的数据向量；θ为参数向量；n(k)为均值为零的随机噪声。

定义模型误差：

ε(k)=F(k)-φT(k)·θ

(10)

使θ满足性能指标J取极小值：

(11)

采用递推最小二乘法进行参数辨识，运用最小方差自适应器进行控制，使得系统输出能跟踪参考信号。其基本思想是：提前d步对输出量进行预测，根据预测值设计所需的控制律，通过连续不断的预测和控制，保证稳态输出方差最小[16]。

考虑挤出过程中的干扰因素，膏体的挤出过程为

F(k)=aF(k-1)+bU(k-1)+(k)

(12)

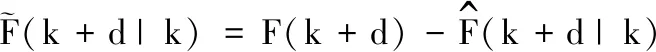
(13)

则性能指标

其中，E(·)为求方差函数。

取预测步长d=1，得到此过程的最优控制量

(14)

其中,Fr(k+1)为提前一步预测的挤压力值。将在线辨识得来的估计参数a、b代入式(14)就可以计算出当前时刻的最优控制量u(k)，通过不断地进行参数估计与更新最优控制量来实现整个过程的实时跟踪控制。a、b由递推最小二乘法辨识得出。A、B缸的参数辨识结果如图6所示。

取图6中参数辨识稳定时的参数作为系统模型参数，则A缸的系统模型为

F1(k)=0.509 3F(k-1)+0.422 6F(k-2)-

9.135 6U(k-1)+1.118 2U(k-2)+v(k-2)

B缸的系统模型为

F2(k)=0.623 7F(k-1)+0.331 2F(k-2)+

6.534 7U(k-1)-1.348U(k-2)+v(k-2)

2.3 FDM材料挤压系统的仿真与实验

2.3.1挤压过程仿真

为了验证上述递推最小二乘法的参数辨识效果和最小方差自适应控制器跟踪期望值的能力，对A、B挤压缸的系统模型进行仿真。为了避免进行最优控制量计算时出现U(1)=∞而导致系统发散的情况出现，设置递推最小二乘法初值如下：数据协方差阵为106I(I为单位阵),θ(0)=(0.001,0.001,0.001,0.001),参考挤压力为周期为60 s的方波信号。在MATLAB下进行仿真，A、B缸对方波信号的响应结果如图7所示。

由图7的仿真结果可以看出，该方法能够较好地跟踪给定的期望挤压力，当期望挤压力发生变化时能够很快进行调整，递推最小二乘法在很短的时间内就辨识出系统的参数，且电压U的值随着F的变化而变化。

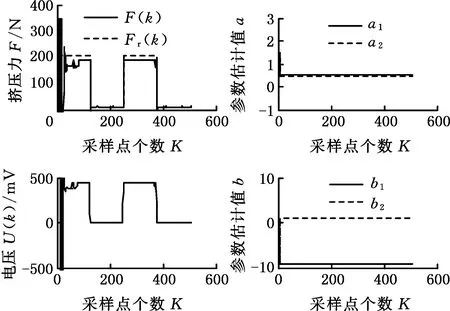
(a)A缸挤压模型对方波信号的响应

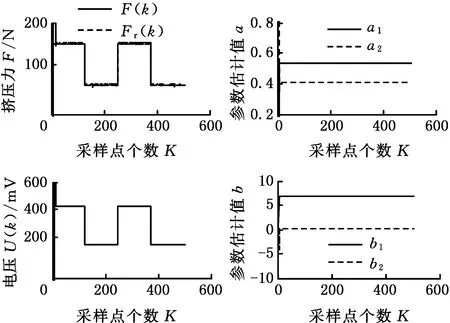
(b)B缸挤压模型对方波信号的响应图7 A、B缸挤压模型对方波信号的响应分析Fig.7 Response analysis of A、B-cylinder extrusion model to square wave signal

2.3.2挤压实验设计

根据仿真结果，尝试设计实验完成该功能梯度材料的混合打印。假设A缸的挤压力设定为

(15)

B缸的挤压力设定为

(16)

即在采样点K<600之前，A、B缸挤压力达到预设值，在K≥600后A、B缸挤压力按式(15)、式(16)变化。

A、B缸混合挤压力和驱动电压的仿真结果如图8所示。则理想状态下(仿真条件下)，挤压缸A的电压变化为

(17)

u1=25U10≤U1≤0.5

挤压缸B的电压变化为

(18)

u2=25U20≤U2≤0.5

式中：u1、u2分别为A、B缸的挤压速度。

喷嘴的移动速度u和两个缸的电压关系为

u=4 444.44(U1+U2)

(19)

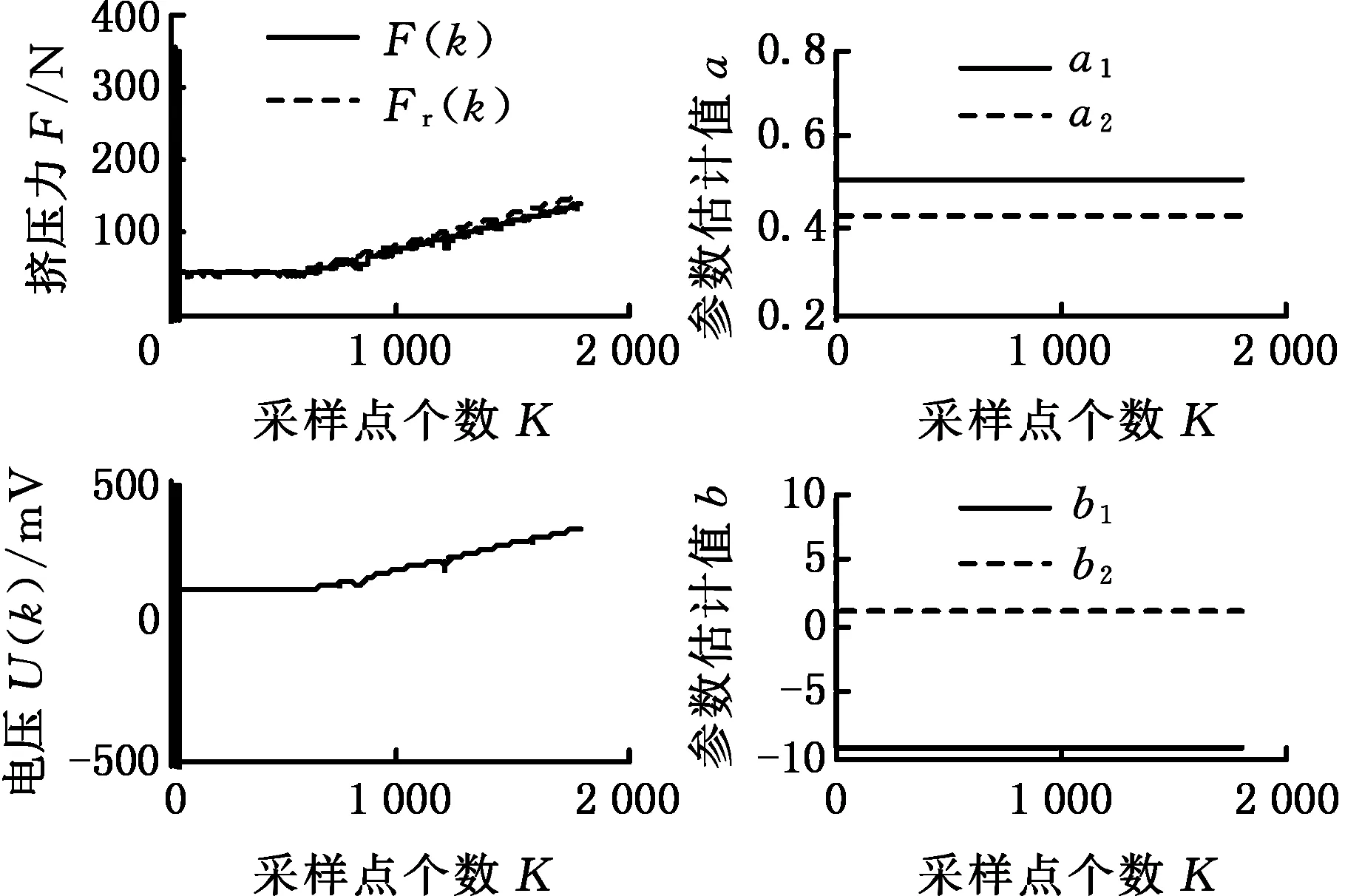
(a)A缸挤压力和驱动电压仿真

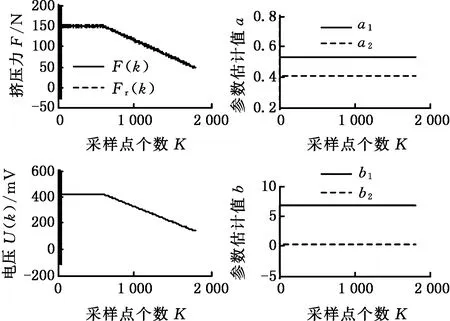
(b)B缸挤压力和驱动电压仿真图8 混和挤压实验A、B缸挤压力和驱动电压的 仿真分析Fig.8 Simulation analysis of cylinder casing pressure and voltage in mixing and extrusion experiment

根据两个缸体电压的变化情况可以看出，实验过程中挤出率η1+η2的变化为

(20)

在K∈(600，1 800)这个时间段，U1+U2从54.37 mV逐渐变为50.23 mV，则可计算出喷嘴移动速度在K∈(600,1 800)这个时间段，从2 416.44 mm/min逐渐变为2 232.44 mm/min。对于实际的挤压工作台来说，此变化范围不大，则实际的实验过程中取喷嘴的移动速度为2 350 mm/min，根据设计的FGM实验进行实验，结果如图9所示。可以看出在K=600之前，挤压缸开始挤压，挤压力逐渐达到预设的150 N和50 N，并保持稳定，当K∈(600,1 800)时，挤压力按照预设的力变化，当K=1 800时，挤压力达到50 N和150 N。

图10为两个缸的驱动电压变化图，图11为两个缸挤压力变化图，可以看出，实际实验过程与仿真结果相一致，验证了假设的正确性。

图10 混合挤压实验驱动电压分析Fig.10 Analysis of squeezing force in mixed extrusion experiment

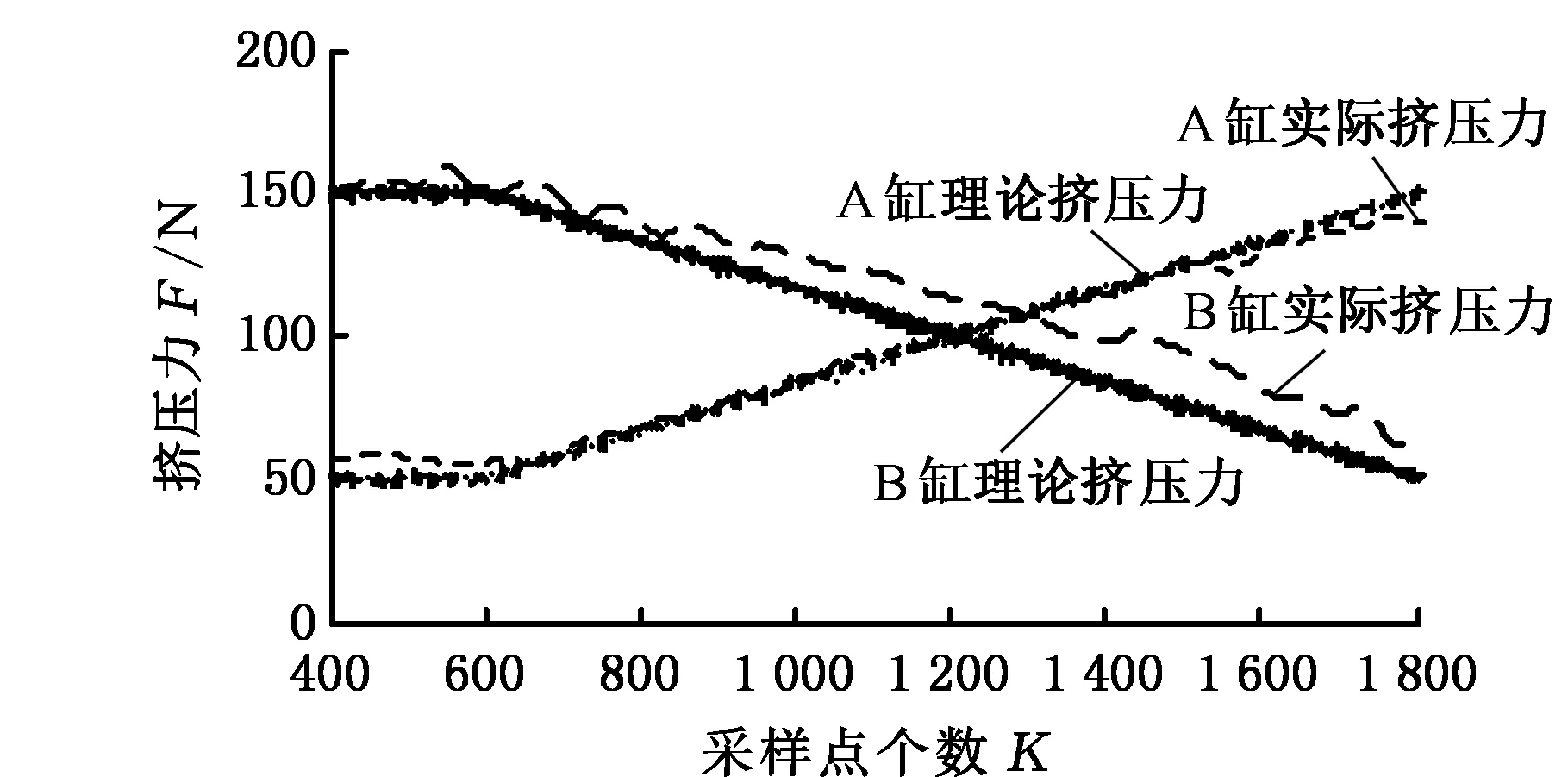
图11 混合挤压实验挤压力分析Fig.11 Analysis of extrusion velocity of mixed extrusion experiment

图12为挤压过程中挤出率的变化曲线。挤出率误差曲线如图13所示。

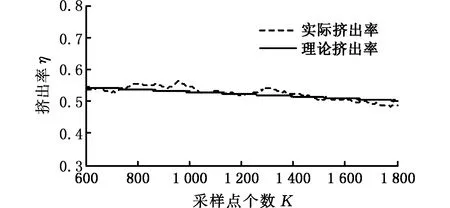
图12 混合挤压实验挤出率分析图Fig.12 Analysis of extrusion rate of mixed extrusion experiment

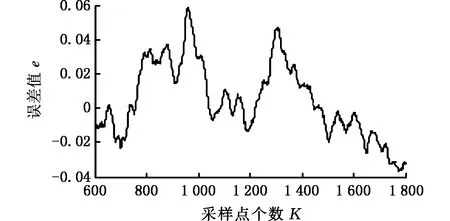
图13 混合挤压实验挤出率误差分析Fig.13 Error analysis of extrusion rate in mixed extrusion experiment

从挤出率的误差曲线(图13)可以看出，在挤压过程中，挤出率的误差保持在-0.04～0.06之间，进一步验证了实验模型、策略方法的准确性和稳定性。进行混合挤压实验时，为了便于直观地显现“梯度”的变化，实验时用蓝、黄两种不同的颜料将腻子粉(CaCO3)分别染色。制备膏体材料时，将腻子粉、水按一定的质量比混合均匀，并分为2份，分别加入蓝、黄两种颜料用以区分，混合均匀后静置10 min，装入挤压缸中，利用图2所示的FGM沉积成形系统进行实验。图14为混合挤压实验挤出效果。

3 结论

(1)对功能梯度材料成形过程建立差分模型，通过残差的方差分析方法和递推最小二乘法对系统模型的阶次和参数进行辨识，得到了成形过程的系统模型，并通过仿真验证了模型的准确性。

(2)运用递推最小二乘法设计了自适应控制器对功能梯度材料成形过程进行实时控制，通过实验验证了控制器的准确性。