基于蜘蛛网结构的伞状可展机构设计与分析

孙建伟 张世梁 孔凡臣

长春工业大学机电工程学院，长春，130012

0 引言

可展机构在航空航天工程中被广泛应用，如卫星天线、航天器等。常见的可展机构以平面剪刀形为主。杨毅等[1]对一种圆柱式折叠结构进行了静力学分析与拓扑布局优化，其基本单元就是剪式机构。陈向阳等[2]分析了常见的一维和二维剪式铰结构的几何特点和可展条件,阐述了复杂剪式铰结构的设计方法和设计原则。刘树青等[3]基于有限元方法对剪式折叠结构进行了力学特性分析。这类可展机构通常具有较高的展收比，但是不具有伞状展开的特点。伞状可展机构由于空间扩展的便利性和有效的承载能力而受到关注。CAO等[4]提出了一种伞状的可展机构，基于可展开单元派生出了一系列具有各种网格形状的单自由度可展机构。KORKMAZ[5]提出了一种基于RRCRR机构单元的新型的伞状机构。赵飞龙等[6]设计了集天线防护罩和可展索网天线于一体的地面伞状可展天线，并进行了形面精度的分析和结构响应分析。胡甜甜[7]设计了一种星载伞状可展开天线，并对其进行了运动学仿真分析与优化。

蜘蛛网是蜘蛛在长期的进化中形成的一种结构简单、规则的结构[8]，它为本文新型伞状可展机构的设计提供了思路。伞状可展机构的承载能力对机构的安全性十分重要。本文根据蜘蛛网承载与散力的特点，分析蛛丝宏观排布对蛛网的影响。蜘蛛网是搭建者的捕食工具与繁殖场所[9-10]，为了保证网面的安全性，其宏观结构在自然选择的过程中得以进化。WIRTH等[11]通过实验发现蜘蛛丝内的张力与蛛丝的疏密程度有关，此外，径向丝与捕丝的节点可以有效地分散蛛丝内力。ZHAO等[12]通过微型3D打印技术搭建了蜘蛛网，通过实验发现蜘蛛网结构拓扑设计影响网的强度，且最佳的拓扑结构也与载荷类型相关。目前大多数对蜘蛛网的仿生设计研究局限于蛛丝本身的材料性能，忽略了蛛丝宏观排布的优势。

本文将蜘蛛网的结构特点应用于伞状可展机构的设计，基于蜘蛛网承载与散力性能的优势，设计伞状可展机构的最优参数，在实现伞状可展的基础上改善机构的力学性能，提高机构的强度和稳定性。

1 模型建立和机构设计

1.1 蜘蛛网结构模型的建立

当蜘蛛网遭受外界冲击力时，可吸收一部分冲击载荷[13-14]，并保持网面的稳定。VOLLRATH等[15]通过实验发现蜘蛛在有外界风力载荷的情况下会搭建更圆的蜘蛛网。如图1所示，完整的蜘蛛网结构包括外围的锚丝与框架丝以及内部的捕丝、径向丝及中心。

图1 蜘蛛网结构模型Fig.1 The structure model of spider web

将蜘蛛网结构简化为只包含径向丝、捕丝和中心的几何结构。如图2所示，粗实线框表示蜘蛛网的中心，虚线表示蜘蛛网的径向丝，细实线表示蜘蛛网的捕丝。六条等长且相邻夹角相等的径向丝与中心连接，三层形状相似的捕丝由径向丝所支撑。根据对捕丝间距规律的研究，模型中捕丝的设计放弃采用连续螺旋线的形式，采用三层闭合有角直线模拟带有弧度的捕丝。中心作为蜘蛛建网的脚手架，在简化的蜘蛛网模型中用正六边形表示。

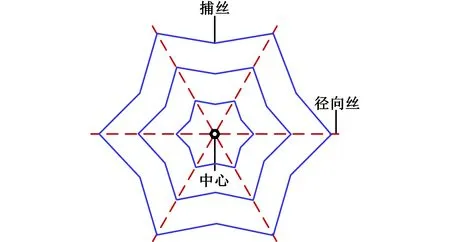
图2 简化的蜘蛛网模型示意图Fig.2 Simplified spider web model schematic

1.2 可展机构单元设计

图3a所示为一个单元的蜘蛛网结构模型，该模型由中心、径向丝及三层捕丝组成。基于图3a的结构单元，设计了图3b所示的具有一个共用滑块的双曲柄滑块机构。该机构作为可展单元由两个平面四杆曲柄滑块机构共用机架组成，这两个机构具有共同的机架A12C12。如图3b所示，曲柄与连杆分别对应蜘蛛网结构中的径向丝与捕丝。机构A12B1C12和A12B2C12共用滑块C12，随着滑块的上下移动，实现了可展单元的收拢与展开的过程。

(a)蜘蛛网结构模型单元 (b)双曲柄滑块机构图3 可展机构单元设计Fig.3 The unit design of deployable mechanism

1.3 结构映射及伞状可展机构组成

蜘蛛网结构模型由6个结构单元依次拼接而成，为实现伞状可展机构的机械性能，将可展单元的运动链在空间中周向分布，通过共用机架、支撑杆和折页组成的连接单元依次连接在一起组成单自由度的伞状可展机构。图4所示为六单元伞状可展机构单元的运动链、连接单元分布和机构的结构形式。根据蜘蛛网模型中径向丝一端与圆网中心顶点相连，并且相邻径向丝夹角为60°的结构特点，设计了伞状可展机构的支撑杆，它通过折页与可展单元相接，实现了可展单元在空间内与支撑杆运动状态相符的展开与收拢过程。

图4 可展单元连接组合方式Fig.4 Connections and combinations of the deployable unit cylinder

2 蜘蛛网结构模型的静力学分析与优化

2.1 最易破坏结构的受力点确定

由于捕丝间距对蜘蛛网结构强度的影响较大，因此首先针对捕丝间距对网面承力性能的影响进行分析。以捕丝夹角为0°建立蜘蛛网结构的三维模型，如图5所示。中心的顶点与三层捕丝顶点的距离分别用d1、d2、d3表示，中心原点与径向丝和中心交点的距离用d0表示。

图5 蜘蛛网结构三维模型Fig.5 Three-dimensional structure model of spider web

把蜘蛛网模型的中心作为固定约束(图6a)，每个径向丝与捕丝的节点以绑定的方式结合。选择模型的6个点作为载荷点，根据伞状可展机构完全展开状态时的受力特点，仅分析其受到垂直于网面的力时的力学性能。在载荷大小及方向相同的情况下对6个点分别进行分析，得到各组的最大应力(图6b)。

由图6b可知，当载荷作用于同一层捕丝时，位于捕丝与径向丝节点处的载荷会对网面造成更大的应力。当载荷作用同一条径向丝与不同层捕丝的节点或不同层捕丝的中点时，远离网面中心处的载荷会造成更大的应力。当载荷作用于径向丝与最外层捕丝的节点处时，所产生的最大应力值最大，此时网面也最易被破坏，因此，本文后续研究都以p3作为载荷点。

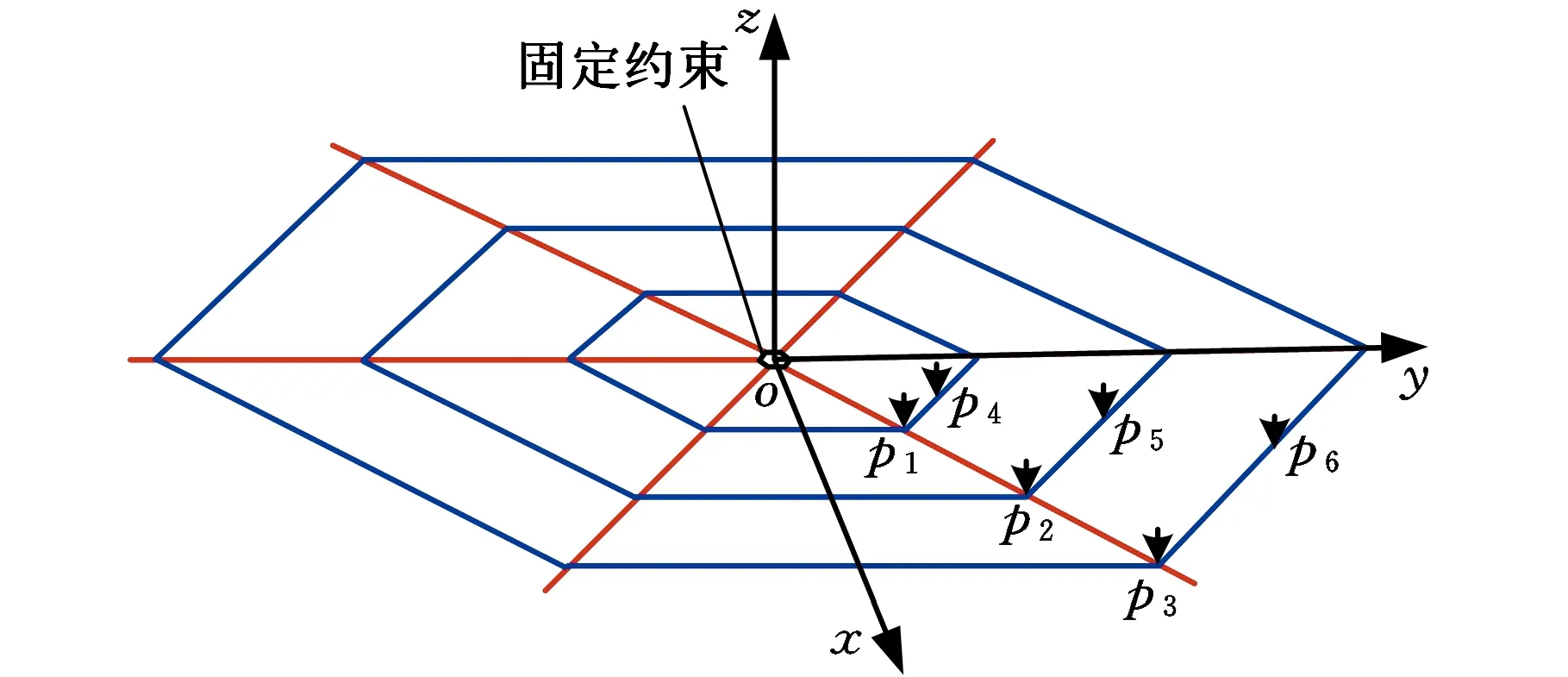
(a)模型受力分布

(b)应力关系图6 蜘蛛网受力情况及应力关系Fig.6 Force situation and the relationship of stress

2.2 蜘蛛网模型捕丝最优间距的确定

VOLLRATH等[16]研究发现，由于某种原因，蜘蛛网的捕丝是一种等间距的阿基米德螺线。但是，这种等间距的排布方式并不一定有利于保证蜘蛛网模型的强度性能。本文针对蜘蛛圆网捕丝的排布规律，探讨蜘蛛网模型中捕丝位置的差异对整个网面承力性能的影响。第3层捕丝的位置固定以保证整个网面尺寸不变，内侧两层捕丝的位置可在一定范围内变化。在相邻两条径向丝间的捕丝是直线的情况下，捕丝位置的变化是通过将六边形捕丝的边长参数化而实现的，在捕丝中心与蛛网中心重合的情况下，改变六边形捕丝的边长实现捕丝位置的移动。

图7为蜘蛛网模型捕丝间距优化示意图,利用ANSYS Workbench的优化模块对结构进行优化。以最大应力值为优化目标，d1、d2为优化变量，其中50 mm0，d1+d2+d3=1 500 mm。图7a中内侧两层捕丝用虚线表示，代表其为优化目标，载荷位置在图中标明；图7b为等间距静力蜘蛛网模型应力云图；图7c、图7d为优化过程的第一步，从200组候选点中筛选出一组最佳的d1、d2值；图7e、图7f表示优化过程的第二步，从较小的范围内通过迭代得到全局最佳的d1、d2值；图7g为优化后蜘蛛网模型示意图，捕丝间距用d′1、d′2、d′3表示; 图7h为优化后的蜘蛛网模型应力云图。最终得到优化后的捕丝间距比例d′1∶d′2∶d′3=1∶2.1∶4。

利用3D打印技术制造了图8所示的两种蜘蛛网模型，两种模型具有相同位置的固定点与载荷点。搭建了图9所示的试验台，利用螺栓杆将蜘蛛网模型固定。利用测力计分别将优化前后的蜘蛛网模型破坏，测得最大载荷值，如图10所示。

图7 捕丝间距优化示意图Fig.7 Optimization schematic of the space between spiral thread

图8 蜘蛛网实体模型Fig.8 Solid model of the spider web

图9 蜘蛛网模型与试验台Fig.9 Spider web model and experiment bench

(a)优化前蜘蛛网模型被破坏的最大载荷值

(b)优后蜘蛛网模型被破坏的最大载荷值图10 测量最大载荷值Fig.10 Measuringthe maximum load value

实验结果表明，优化后的蜘蛛网模型更不易被破坏，其强度性能有所提高。实验结果在一定程度上证明了仿真优化的正确性。

2.3 蜘蛛网模型捕丝角度优化

捕丝具有一定的夹角可以有效地逐级分散冲击载荷。为得到蜘蛛网模型受到垂直于网面的载荷时，捕丝夹角α变化对单层蜘蛛网模型节点位移的影响，将单层蜘蛛网模型看作一种钢架结构，其每一个节点都为刚性连接，其中心作为固定约束，利用矩阵位移法计算各节点的位移及最大应力(图11)。

图11 单层蜘蛛网钢架模型Fig.11 Steel frame model of single layer spider web

本文对蜘蛛网结构性能的研究是针对外界载荷为垂直于网面的情况下进行的，因此将单层蜘蛛网钢架结构视为空间钢架，利用结构力学中的矩阵位移法进行计算。空间钢架单元的每个节点具有6个自由度，即为(ux,uy,uz,θx,θy,θx)，因此每个杆单元具有12个自由度。对于一有n个节点的钢架结构, 其整体刚度矩阵K为6n×6n的矩阵。由图11可知，单层蜘蛛网结构钢架具有12个节点，因此该结构的整体刚度矩阵K为72×72的矩阵。

在局部坐标系下，杆li(li为杆件编号,i=1,2,3,4)的单元刚度矩阵可以表示为

(1)

利用坐标转换矩阵将局部坐标系下的单元刚度矩阵转换在整体坐标系中：

(2)

其中,转换矩阵Rli为

(3)

(4)

式中,θx′x为x轴与x′轴的夹角，其他类推。

杆件1、2、3、4构成一组结构单元，将其刚度矩阵进行集成，得

(5)

按照杆件之间的连接关系将每个结构单元进行集成得到72×72的整体刚度矩阵K。

单层蜘蛛网结构钢架共由18个杆件刚性连接而成，通过矩阵位移法建立荷载与位移之间的关系：

KU=F

(6)

式中,U为结构节点位移矢量；F为结构节点载荷矢量。

进而计算杆件1中的杆端内力：

f=k′rU+F

(7)

式中,k′为整体刚度系数。

然后将杆1视为悬臂梁，计算其最大应力：

(8)

式中，M为杆件的截面弯矩；ymax为受力点到中性轴的最大距离；Iz为杆件的截面惯性矩。

横截面弯矩M=FL，取载荷F=10 N，杆长L分别取400 mm、450 mm、500 mm，横截面为边长是5 mm的正方形，利用MATLAB建立了单层蜘蛛网的整体刚度矩阵，计算其最大应力值随角度变化，如图12所示。由图12可知，在捕丝角度α=7°时最大应力值最小，因此，蜘蛛网模型捕丝夹角取7°时，网面的强度性能最优。

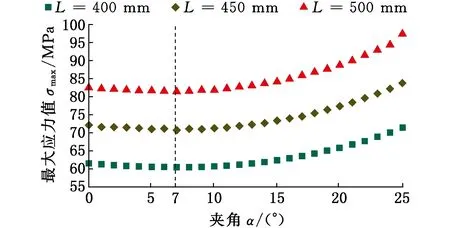
图12 最大应力值与捕丝夹角关系Fig.12 The relationship between maximum stress and angle

3 伞状可展机构参数设计及仿真

3.1 参数设计

伞状可展机构在收拢、展开及完全展开过程中，其各个可展单元和连接单元相对于机架具有相同的空间位形，因此任选机构中的一个连接单元以及相邻的两个可展单元，结合机架正多边形的性质，由可展机构完全展开成平面的状态即可得出伞状可展机构的参数。图13所示为伞状可展机构的参数模型。

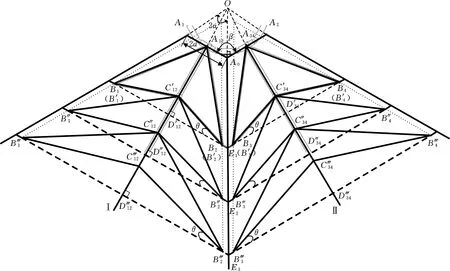
图13 伞状可展机构的参数模型Fig.13 The Parameter model of the umbrella-type deployable mechanism

O为机架重心，A1、A0、A2为机架的顶点，A1A0、A0A2为机架的边，OA12⊥A1A0、|A1A12|=|A12A0|，OA34⊥A0A2，|A0A34|=|A34A2|;∠A1OA0=∠A2OA0=2α,∠A1OA0为机架的边对应的圆心角，β为机架相邻边的夹角，OA0为β的角平分线，∠A1A0O=∠OA0A2=β/2；A12C‴12、A34C‴34分别为可展单元Ⅰ和Ⅱ的滑块导轨，A12C‴12、A34C‴34分别与OA12、OA34共线，A0E3为支撑杆,与OA0共线；A12B′1C′12B′2为可展单元Ⅰ的一级展开单元，∠C″12B′2B′1=θ。A12B1D′12B2为充分利用杆长时的一级展开单元，此时θ°=0，B1B2⊥A12C‴12；C′12B‴1C″12B‴2、C″12B‴1C‴12B‴2分别为可展单元Ⅰ的二级和三级展开单元，∠C‴12B″2B″1=∠C‴12B‴2B‴1=θ，同样地，A34B′3C′34B4为可展单元Ⅱ的一级展开单元，A34B3D′34B4为充分利用杆长时的一级展开单元，此时θ=0°,B3B4⊥A34C‴34；C′34B‴3C″34B‴4、C″34B‴3C‴34B‴4分别为可展单元Ⅱ的二级和三级展开单元，∠C″34B″3B″4=∠C‴34B‴3B‴4=θ；B2E1B3、B″2E2B″3与B‴2E3B‴3分别为可展单元Ⅰ、Ⅱ的一级展开单元、二级展开单元和三级展开单元的折页连接组件，E1、E2和E3分别为折页连接组件与支撑杆A0E3的交点，每个折页的长度都是相等的，B2E1=E1B3=B″2E2=E2B″3=B‴2E3=E3B‴3。

根据前文对蜘蛛网结构模型的分析与计算，得到其最佳比例关系及捕丝角度。基于蜘蛛网结构的最优参数，令A0E1∶E1E2∶E2E3=1∶2.1∶4，∠B′1B′2C′12=∠B″1B″2C″12=∠B‴1B‴2C‴12=7°。

3.2 三层伞状可展机构仿真

为了证明仿蜘蛛网结构模型的伞状可展机构相对于优化之前的等比例伞状可展机构具有更好的受力性能，利用ANSYS Workbench软件对4组机构进行了静力分析。为了尽量体现支撑杆的承力作用并模拟蜘蛛网结构模型，在静力仿真时，去除了支持滑块移动的轨道杆。基于优化前的三层等比例伞状可展机构，建立了优化过程中3个阶段的机构模型用以仿真对比。图14a为等比例、连杆无角伞状可展机构；图14b为等比例、连杆有角伞状可展机构；图14c为优化比例、连杆无角伞状可展机构；图14d为优化比例、连杆有角伞状可展机构。对4组机构在蜘蛛网模型受最大应力的相同位置与方向施加相同大小的外力，以其机架作为固定约束。

施加载荷后，4组机构的等效应力值仿真分析结果如图15所示。由图15可知，受到相同载荷时，优化前的等比例无角伞状可展机构的最大应力值高于其他3组机构，表明其受力性能较差。仿蜘蛛网结构的伞状可展机构的最大应力值相对较小，表明其受力性能最优。

4 伞状可展机构样机实验

基于本文对伞状可展机构的设计，利用3D打印技术搭建了伞状可展机构的实体模型。如图16所示，通过伞状可展机构的实体模型可以更直观地展示其展开过程。

(a)等比例、连杆无角(b)等比例、连杆有角

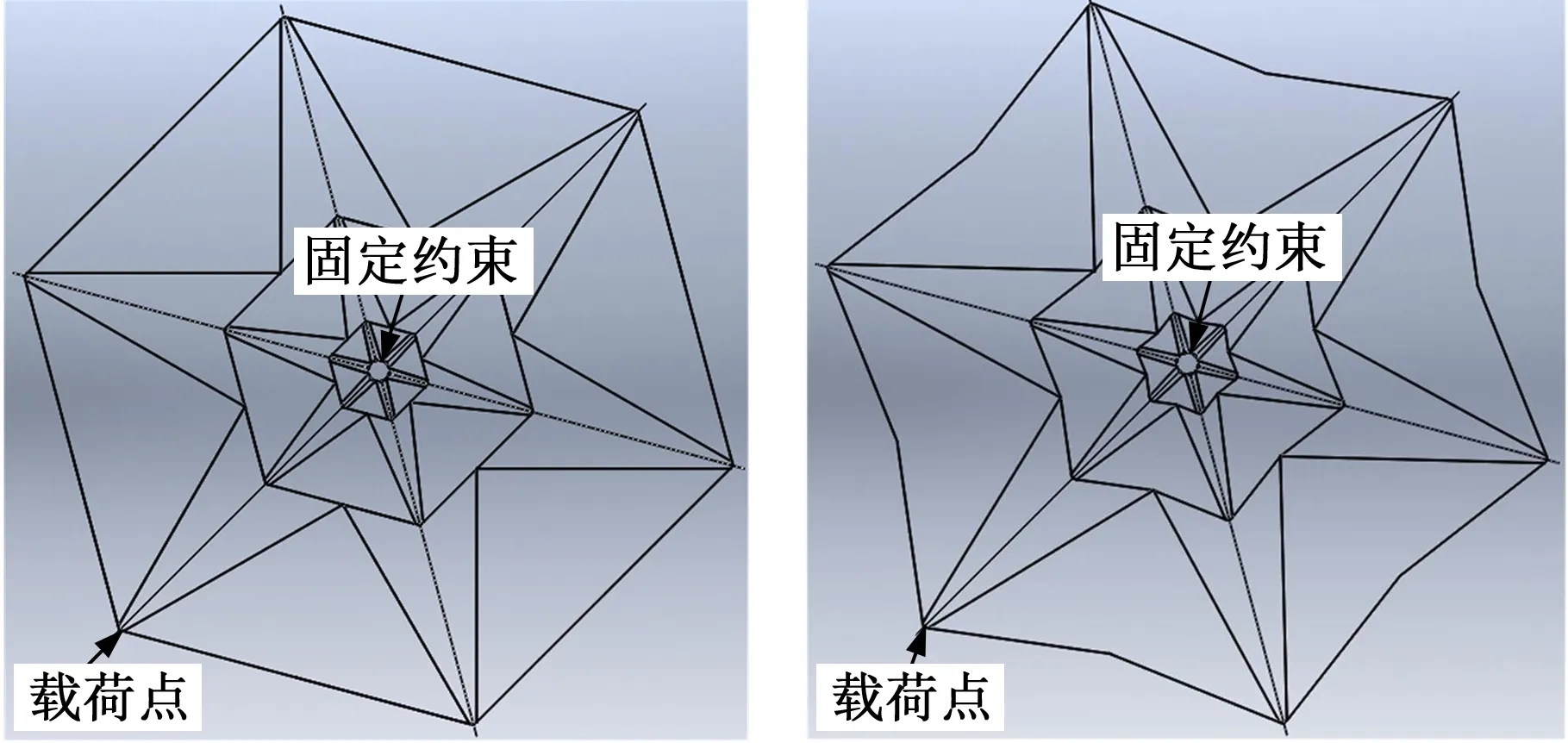
(c)优化比例、连杆无角(d)优化比例、连杆有角图14 完全展开状态下伞状可展机构模型对比Fig.14 Comparison of umbrella-type deployable mechanism models in full deployment

(a)等比例、连杆无角

(b)等比例、连杆有角

(c)优化比例、连杆无角

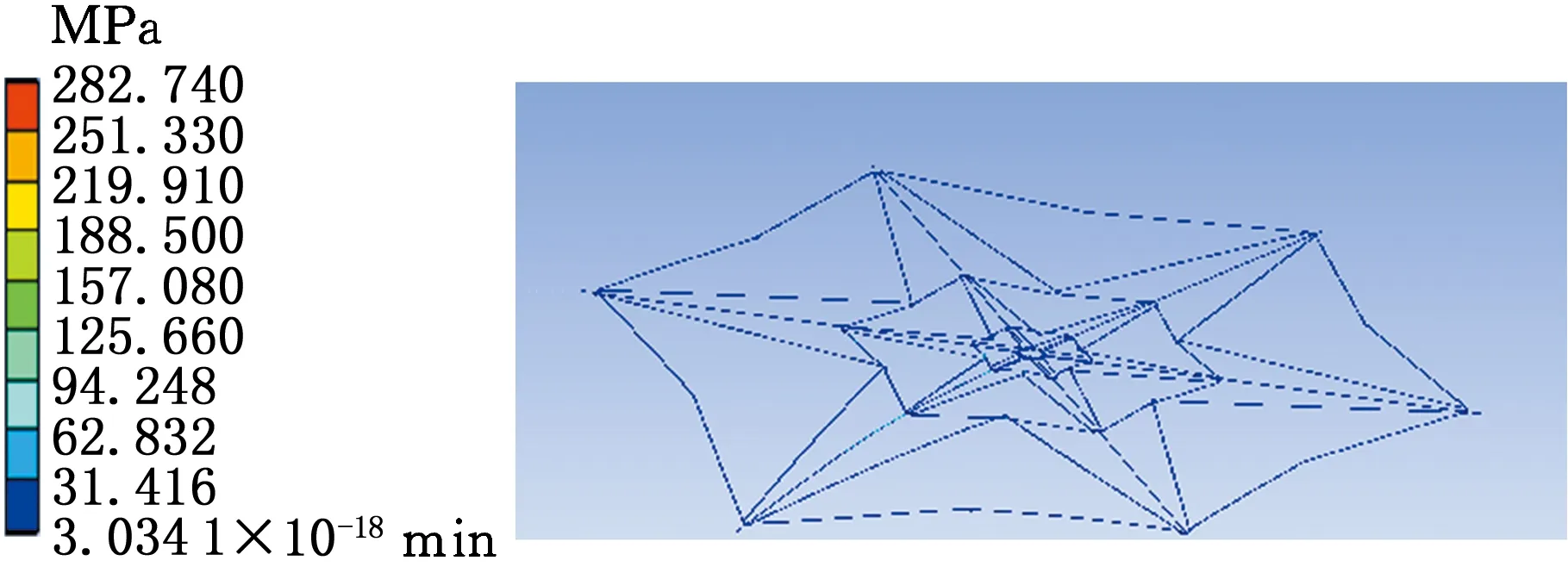
(d)优化比例、连杆有角图15 伞状可展机构应力云图Fig.15 The stress cloud of umbrella-type deployable mechanism

(a)收拢状态

(b)中间状态

(c)展开状态图16 伞状可展机构展开过程Fig.16 The expansion process of umbrella-type deployable mechanism

5 结论

本文基于蜘蛛网结构提出了一种以曲柄滑块机构为可展单元的伞状可展机构，该机构具有伞状展收的特征。基于蜘蛛网的结构模型，考虑捕丝间距对蜘蛛网结构承力性能的影响，利用静力学分析与优化，得出捕丝间距的比例为1∶2.1∶4。基于单层蜘蛛网结构的钢架模型，考虑捕丝夹角对结构承力性能的影响，通过矩阵位移法，得出捕丝的最优夹角为7°。基于对蜘蛛网模型的分析与优化，得到强度性能最佳的伞状可展机构，仿真分析验证了其强度性能有所提升。