基于T-Map的飞机部件交点轴线公差转化方法

肖 欢 朱永国 刘春锋 周结华

1.南昌航空大学航空制造工程学院，南昌，3300632.金航数码科技有限责任公司，北京，1000283. 江西洪都航空工业集团有限责任公司部装一厂，南昌，3300244. 南昌航空大学信息工程学院，南昌，330063

0 引言

飞机部件这种大型装配件的对接装配、测量过程中所使用的激光跟踪仪、局部GPS等飞机数字化装配精度检测设备得到迅速发展与应用，但这些数字化检测设备都是基于点测量模式的，以测量点的坐标值变动来评价装配准确度[1]。考虑到装配中的装配可行性、定位稳定性等因素，采用数字化设备对装配件进行精度检测需要对传统的装配方案进行调整。由于调整后装配基准的变化致使装配特征间的约束关系、几何公差都产生变化，故要满足设计要求必须重新进行公差计算与分配。为了获得基准变换后基于点测量模式装配方案的几何公差，需要探索合理的公差转化方法。

国内外学者在公差表示和公差转化方面已经取得了一些成果。DESROCHERS[2]提出了工艺和拓扑相关表面(TTRS) 的几何尺寸和公差(geometric dimension and tolerance,GD&T)表示方法，通过构建TTRS的公差转化模型进行了公差转化分析。THIMM等[3]为实现公差方案从设计到工艺的转化，依据几何公差的类型定义进行规划，以满足设计与制造要求为前提，提高设计的可制造性为目的，进行了几何公差转化系统开发。LOUATI等[4]在小位移矢量簇(SDT)理论基础上，通过功能几何与基准几何空间位置的变换求解，获得了三维几何模型的公差约束条件，提出了基于SDT的几何公差直接转换方法。CAUX等[5]为实现几何公差的转换，通过基准参考系下变动几何空间位置的矢量变换，提出了一种基于矢量表示的公差转换方法。ANSELMETTI[6]通过公差链的微分变动分析，提出了满足ISO标准制造规范的线性模型公差转换算法。胡洁等[7]提出了面向装配的变动几何约束网络概念，将变动几何进行统一描述，建立了形位公差与几何公差综合的公差转化模型。张开富等[8]提出了基于关键特征和图的装配容差表示方法，建立了基于有向图的、集成尺寸、形位及配合容差的装配容差模型。胡伟等[9]建立了装配精度信息模型，分析了航天器装配关键节点的公差作用影响以及不同几何坐标系下的装配公差作用转化机理，实现了装配精度预测。鲍强伟等[10-11]为了研究尺寸及公差单元几何特征之间的转换关系，根据几何特征与信息单元的映射关系对功能几何相关的公差累积方程进行了推导，通过确定设计基准、定位基准和功能几何位置信息，实现了装配模型信息的层次化解析。

上述研究为公差转化方法求解提供了不同思路，但仍存在以下问题：①TTRS理论、SDT理论都未对基准之间相互约束自由度下的公差转化进行分析，只是从基准体系约束下功能几何自由度的角度考虑公差转化，容易导致基准体系冗余或过约束；②上述方法都是利用公差漂移边界求解几何公差变动区域，并且都是对部分几何公差类型进行解析，缺乏对自由度约束下的几何公差求解，与美国机械工程师协会(ASME)标准对几何公差的定义不一致；③上述方法并没有在测量点的坐标值变动层面考虑几何公差的变化，不适用于基于点测量模式的数字化装配设备。

针对上述总结的3点问题，本文提出了一种基于公差图(T-Map)的公差转化方法。T-Map公差模型是将几何特征映射到欧氏空间的点空间模型，T-Map中的每个映射点对应几何特征的每一个可能的变动位置，能够直观表示相同特征上的多个公差和在一个或多个指定修改材料条件的基准特征，其边界表示偏差范围。DAVIDSON等[12]建立了标准平面特征的T-Map公差模型，BHIDE等[13]建立了圆柱特征的T-Map公差模型，在此基础上，JIANG等[14]通过构建T-Map，对零件加工过程中圆柱特征基准转换后加工公差的合理性进行了验证。本文基于T-Map与ASME标准兼容以及表达直观简洁等特点，将T-Map作为公差转化的公差数学模型，以交点轴线为研究对象，构建交点轴线的T-Map，提出基于T-Map的飞机部件交点轴线公差转化方法。

1 基于T-Map的交点轴线公差模型构建

飞机装配协调中，交点轴线指两交点连线，属于直线类特征，其公差域为圆柱域。图1表示交点轴线的变动区域，受4个自由度方向约束，其理论轴线可沿两个平动方向Tx、Ty和绕两个转动方向Rx、Ry变动，理论轴线轴长为l，公差域大小为T，圆柱域的坐标系Ocxcyczc位于圆柱几何中心。

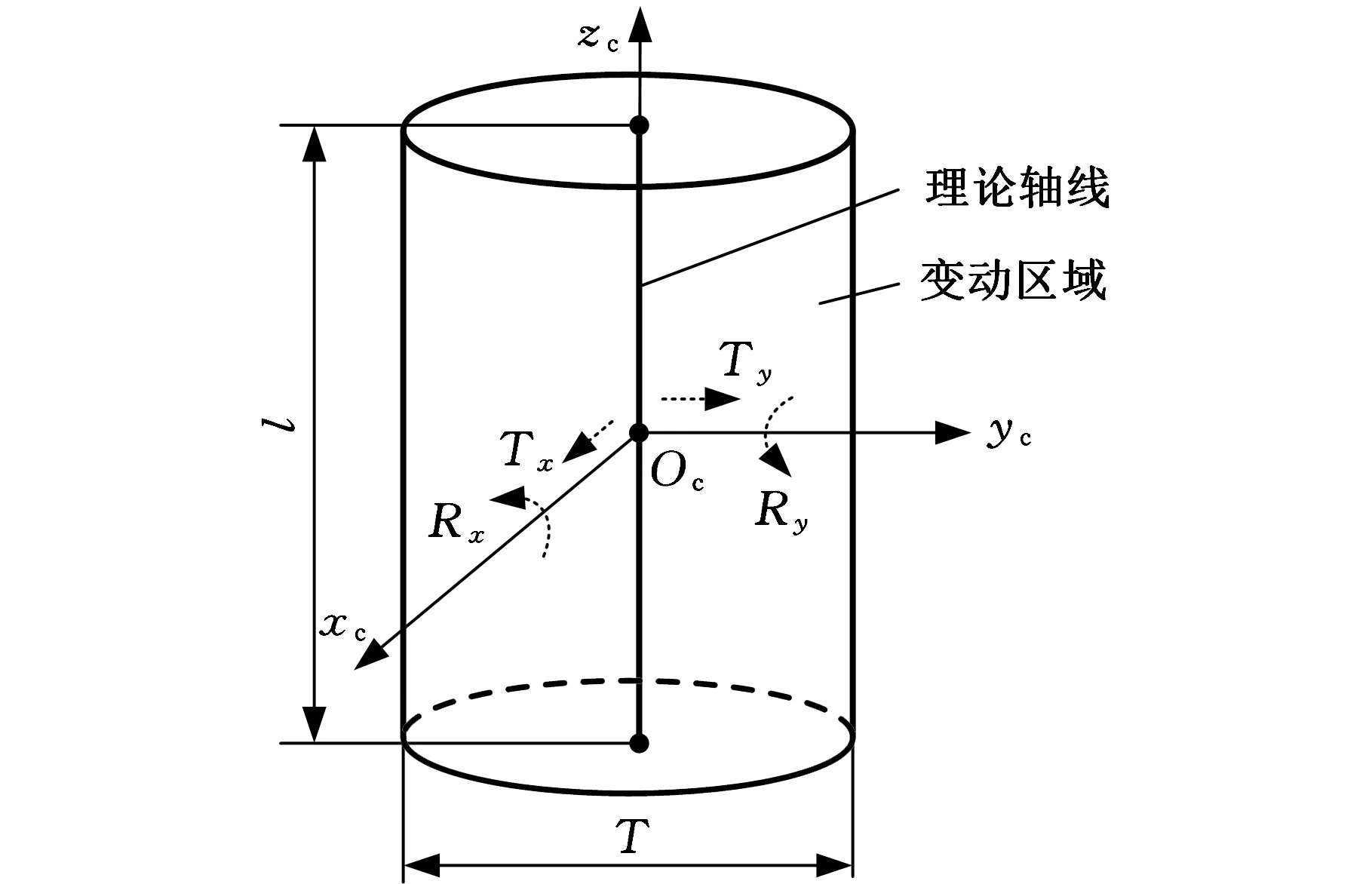
图1 交点轴线的变动区域Fig.1 The variable domain of Intersection axis

将交点轴线的变动映射为T-Map，T-Map的每个坐标轴对应一个自由度方向，但由于转动与平动的单位分别是角度与长度，使得T-Map各坐标轴的单位不统一,因此，利用等效线性变换对T-Map各坐标轴单位进行统一。三维空间中的直线可由Plücker坐标(L,M,N,P,Q,R)表示，其中，L、M、N表示直线的方向变动量，P、Q、R表示直线的位置变动量[15]。图1中，实际轴线相对理论轴线在Rx、Ry方向的变动量分别对应M、L，在Tx、Ty方向的变动量分别对应P、Q。设圆柱域上下表面中任意点的坐标分别为p1(x1,y1,z1)和p2(x2,y2,z2)，则有z1=l/2，z2=-l/2。建立三维空间直线Plücker坐标与p1、p2的关系：

(1)

式(1)中，理论轴线轴长l是定值，所以N为定值；R是T的2阶小项，可忽略不计。依据式(1)，利用Mv=lM/2和Lv=lL/2，对转动变动量进行等效线性变换。考虑N为定值和R为可忽略的高阶小项，将交点轴线对应于T-Map中的映射点表示为Ω(P,Q,Mv,Lv)，该映射点能够在欧氏空间中进行表示。另外，各自由度方向的偏差波动彼此相关，受公差域约束的交点轴线T-Map的边界方程为

(2)

式(2)的几何意义是四维空间中的两个曲面相交的部分为交点轴线T-Map边界。为此，设Ω(P,Q,Mv,Lv)中某项为0，则可在三维空间中表示映射点的波动范围，如Mv=0时的交点轴线T-Map见图2。

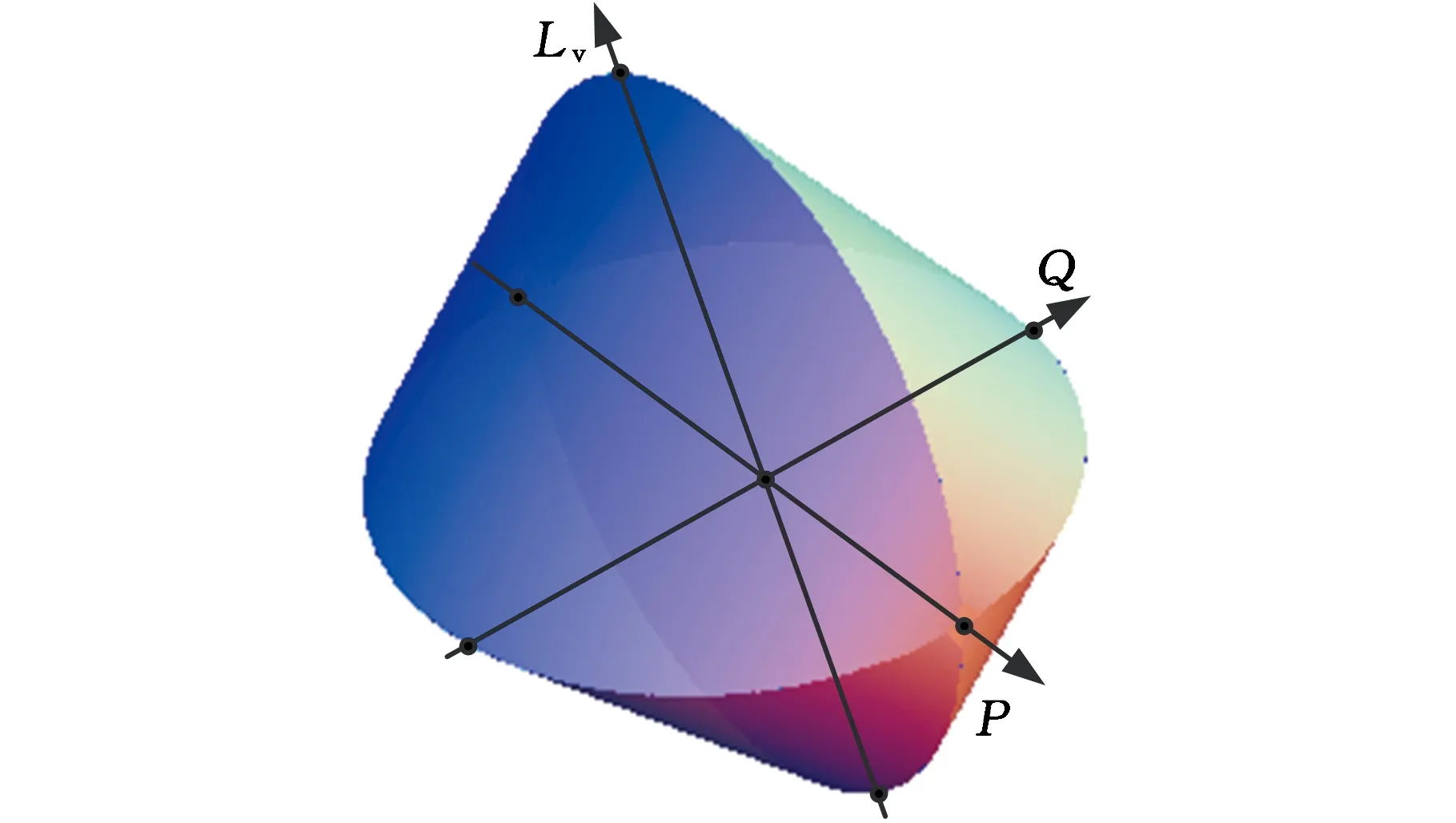
图2 Mv=0时的交点轴线T-Map Fig.2 T-Map of intersection axis when Mv=0

2 交点轴线基准变换模型构建

交点轴线装配方案调整后，基准的变换致使特征的相对位置和GD&T发生改变，为了方便描述基准变换前后交点轴线相对位置与GD&T的关系，需构造一个表示基准变换前后相关参数转化关系的模型。

2.1 交点轴线相对位置关系构建

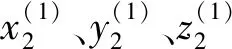
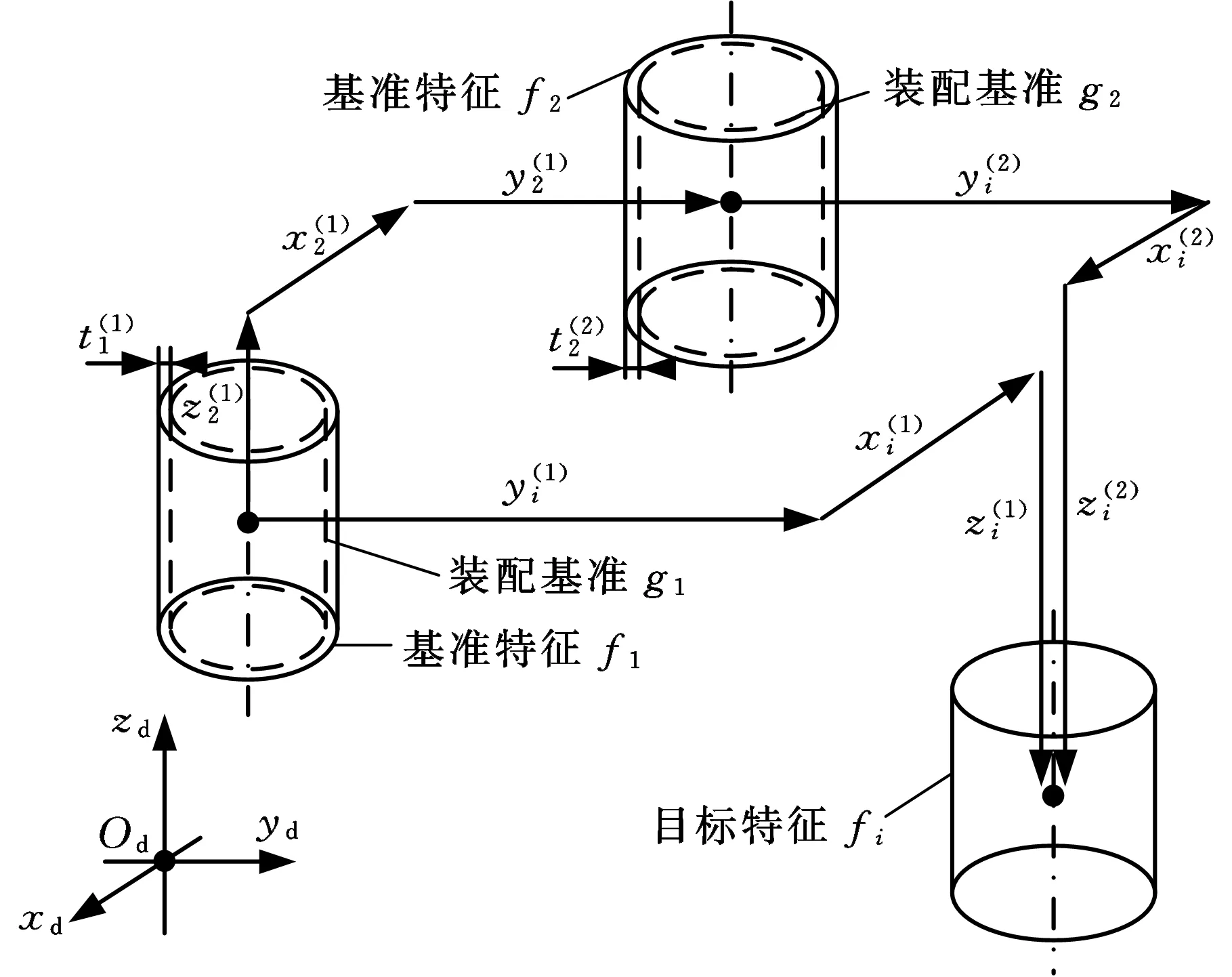
图3 集成GD&T的交点轴线基准变换相对位置关系Fig.3 Integrated GD&T’s intersection axes datum transformation relative positional relationship

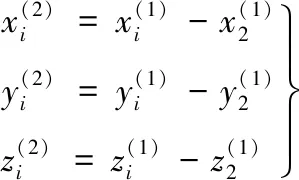
(3)

式(3)说明装配方案调整后，目标特征与装配基准的位置关系已发生变化，为此，将相对位置关系与GD&T进行统一表示：

(4)

i∈{1,2,…,n}j∈{1,2}

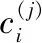
2.2 基于GD&T的T-Map解析

装配基准变换会使装配方案中的参考关系发生改变，导致特征的约束关系也发生改变，为满足设计要求，此时需要重新求解合适公差。对于实际装配过程，以目标特征的实际参考为装配基准，目标特征与装配基准不一定一致。

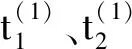
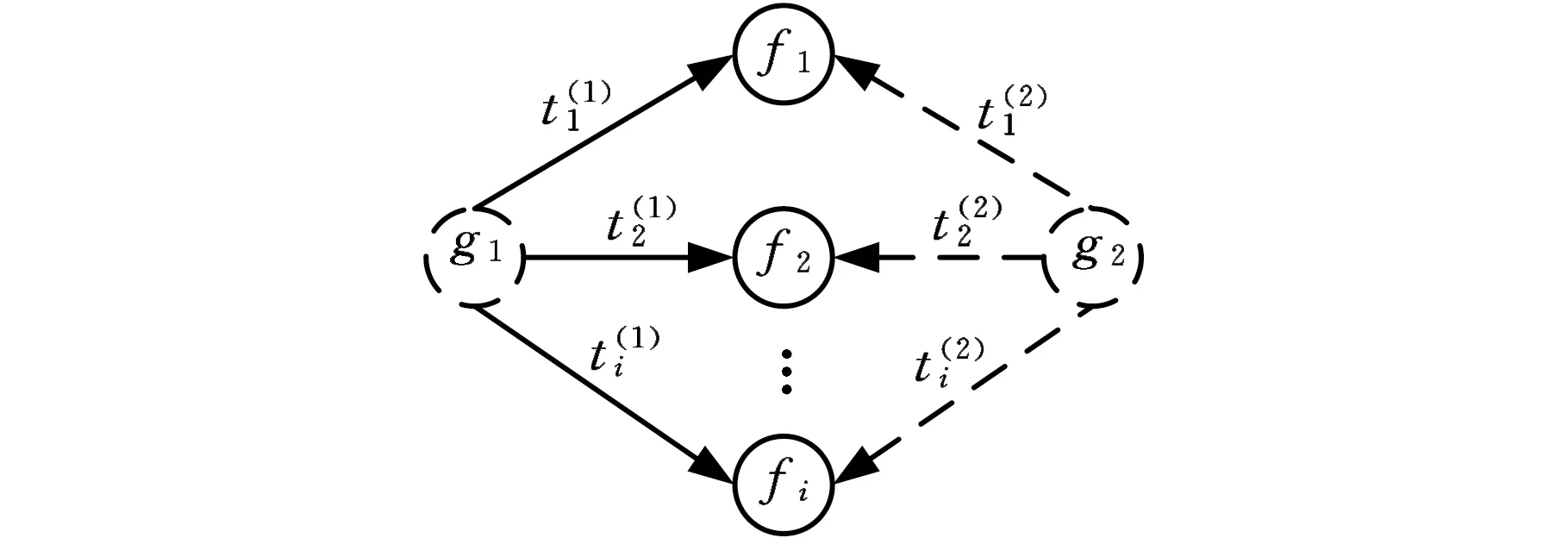
图4 基于有向图的基准变换前后GD&T关系模型Fig.4 The GD&T relation model with before and after datum transformation based on directed graph

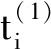
(5)

(6)

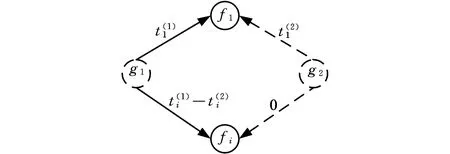
图5 GD&T关系调整后的公差回路Fig.5 The adjusted tolerance loop of GD&T relationship

3 基准变换下的交点轴线T-Map重构

装配方案调整后，交点轴线的变动会因基准变换影响其他特征，交点轴线的T-Map也会相应改变,为此，需要对基准变换后交点轴线T-Map公差模型进行重构。首先，通过解析交点轴线变动关系得到目标特征在各自由度上的变动量；然后，求解各自由度上的变动量，获得目标特征T-Map映射点坐标；最后，依据基准变换关系，得到基准变换后的交点轴线T-Map公差模型边界。

3.1 面向基准变换的交点轴线变动分析

利用文献[16]给出的偏差传递状态空间方程可得f1、g1和g2间的累积变化公式：

(7)

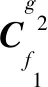
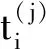
(8)

由式(8)可得

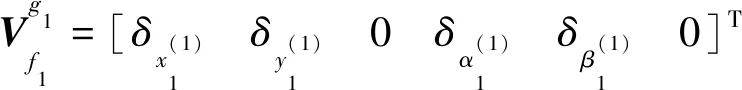
(9)

同理，建立fi、g1和g2间的累积变化关系：

(10)

(11)

将式(9)代入式(11)得

(12)

(13)

3.2 目标特征T-Map映射点坐标计算

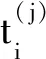
(14)

(15)

式中，li为特征fi的理论轴长。

(16)

3.3 基准变换后的T-Map边界解析

(17)

根据式(2)和式(17)，基准变换后，fi的T-Map边界方程为

(18)

(19)

依据式(18)和式(19)，基准变换后fi的T-Map映射点的约束条件为

(20)

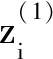
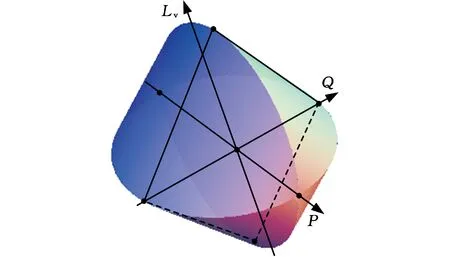
图6 当Mv=0时，基准变换后的交点轴线T-MapFig.6 The intersection axis T-Map after the datum transformation(Mv=0)

4 ST-Map最小约束条件求解

4.1 基准变换后T-Map的2维空间域求解

依据式(20)，选用Lv-Q或Mv-P方向的二维空间域作为判断依据。基准变换后在Lv-Q与Mv-P方向二维空间域的约束条件分别为

(21)

(22)

(23)

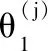
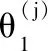
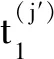
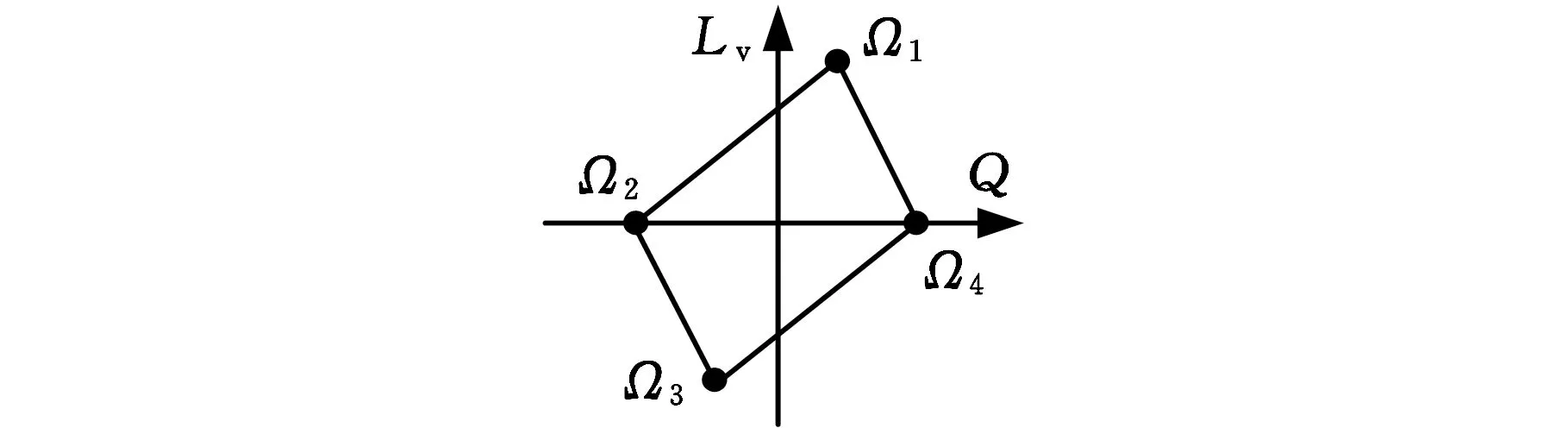
图7 基准变换后Lv-Q方向的二维空间域Fig.7 The Lv-Q direction’s two-dimensional spatial domains after the datum transformation 表1 图7中4个极限映射点坐标Tab.1 4 limit map point coordinates in figure 7

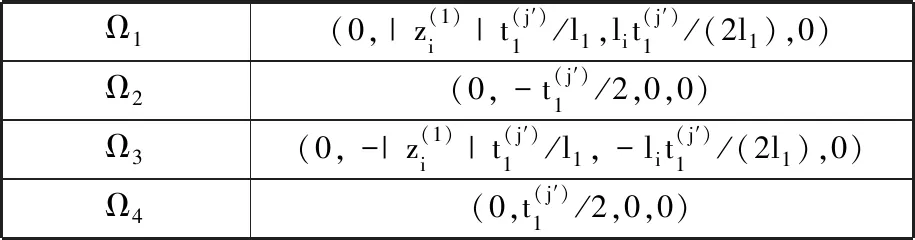
Ω1(0,|z(1)i|t(j′)1/l1,lit(j′)1/(2l1),0)Ω2(0,-t(j′)1/2,0,0)Ω3(0,-|z(1)i|t(j′)1/l1,-lit(j′)1/(2l1),0)Ω4(0,t(j′)1/2,0,0)

4.2 ST-Map的二维空间域求解

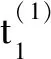
(24)

依据式(21)、式(22)和式(24)，可得ST-Map在Lv-Q和Mv-P方向二维空间域的约束条件：

(25)

(26)

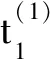
4.3 二维空间域几何关系的比较

在基准变换前的T-Map中，Lv-Q与Mv-P方向的二维空间域形状依据式(2)可知都为正方形，那么在正方形边界上任意一点的坐标值之和必为定值。由此，为得到某方向的最小约束条件只需确定ST-Map对应方向二维空间域上最大坐标值之和的映射点即可。用Lv-Q方向的二维空间域进行说明，ST-Map由变换后的T-Map累积获得，其Lv-Q方向的二维空间域为凸多边形，则映射点最大坐标值之和在其边界的4个极限映射点之中。通过表2的信息可获得图9所示ST-Map与基准变换前T-Map的二维空间域几何关系。最小约束条件为

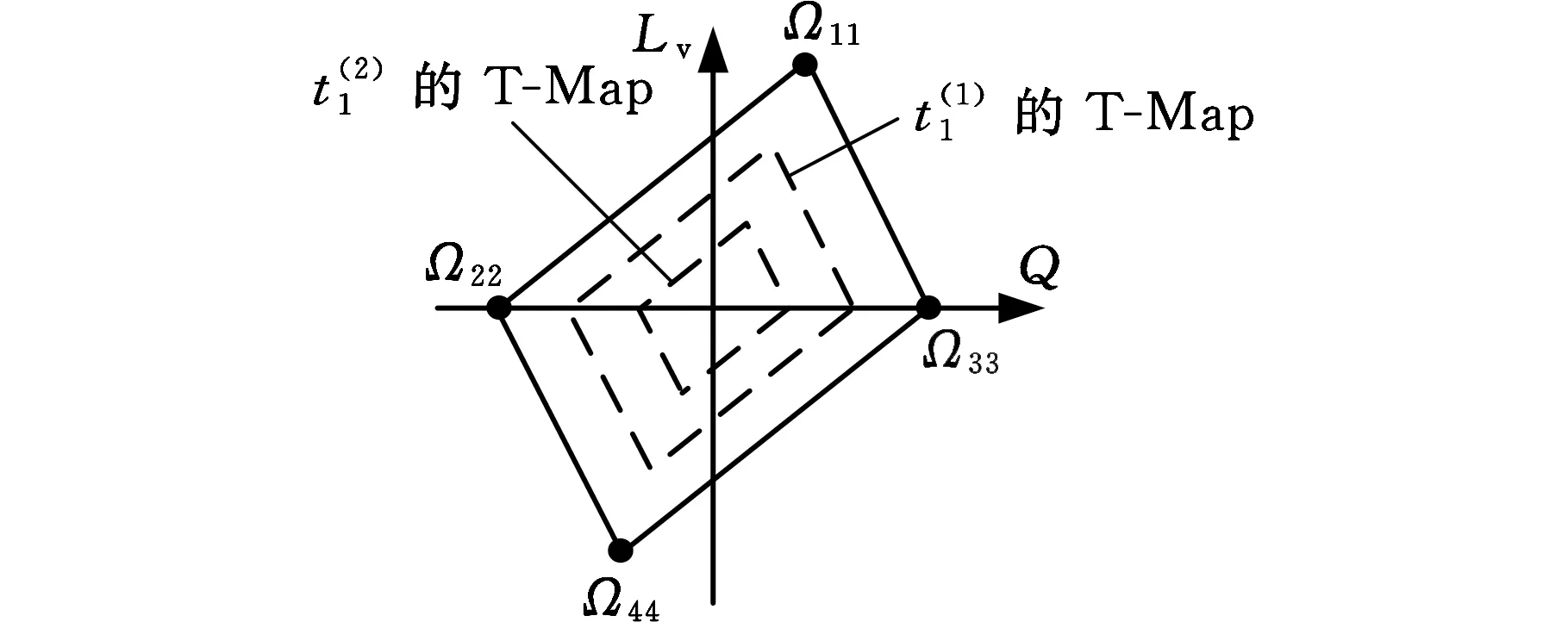
图8 ST-Map在Lv-Q方向的二维空间域Fig.8 The Lv-Q direction’s two-dimensional spatial domains of ST-Map 表2 图8中4个极限映射点坐标Tab.2 4 limit map point coordinates in figure 8

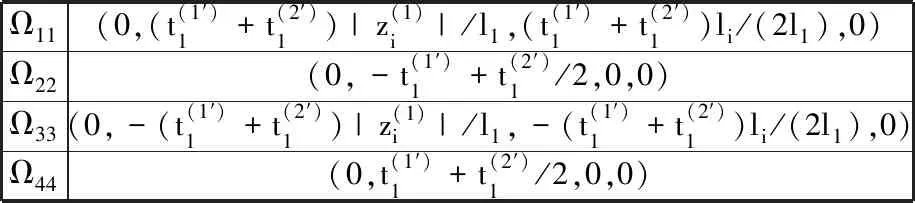
Ω11(0,(t(1′)1+t(2′)1)|z(1)i|/l1,(t(1′)1+t(2′)1)li/(2l1),0)Ω22(0,-t(1′)1+t(2′)1/2,0,0)Ω33(0,-(t(1′)1+t(2′)1)|z(1)i|/l1,-(t(1′)1+t(2′)1)li/(2l1),0)Ω44(0,t(1′)1+t(2′)1/2,0,0)

Lvi=

(27)

类似地，可得图9所示Mv-P方向的二维空间域几何关系。最小约束条件为

Mvi=

(28)

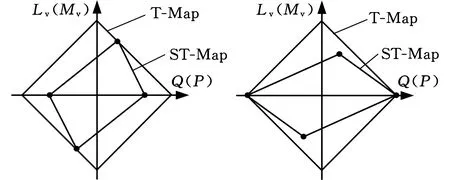
图9 Lv-Q方向和Mv-P方向二维空间域 几何关系比较Fig.9 The geometrical comparison of Lv-Q direction and Mv-P direction’s two-dimensional spatial domains

5 基于T-Map的交点轴线公差转化

在实际装配中，交点轴线的约束自由度方向因位置、方向及基准优先性而被基准特征限制，故在公差转化过程中仅需考虑部分自由度的约束。另外T-Map与ST-Map的变动范围在基准变换公差转换过程中会因公差大小而受限制，为此，可比较不同自由度约束情况下T-Map与ST-Map的几何关系，分别进行最大可能公差值的求解，从而获得基准变换前后公差的约束条件，即基于T-Map的公差转化关系。

5.1 4自由度约束的最大公差值求解

4个自由度方向约束下的交点轴线，其T-Map的Lv-Q方向与Mv-P方向的二维空间域的约束条件都必须满足，那么基准变换前的T-Map与满足式(27)及式(28)条件的ST-Map的二维空间域相等，T-Map的边界方程为

(29)

(30)

式中，Ti为变换前T-Map的公差值；ci为2种情况下最小约束条件的统一系数。

ST-Map与T-Map的二维空间域必须相等，因此需确定Ti的最大值。由式(29)可知：

Ti=

(31)

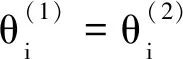
(32)

5.2 3自由度约束的最大公差值求解

假设受P、Lv和Mv方向约束，则原T-Map应满足：

(33)

由式(33)和式(28)可知，Ti的T-Map的边界方程为

(34)

式(34)右边项可认为是如下两个椭圆坐标轴X和Y的坐标：

(35)

由于式(35)表示的两椭圆形状相同，则其Minkowski和为

(36)

依据式(36)，Ti的最大值为

(37)

(38)

由式(38)可知，式(37)中的max(Ti)与式(32)中的max(Ti)相同。

5.3 2自由度约束的最大公差值求解

假设受P和Q方向约束，则原T-Map应满足：

(39)

Ti的T-Map边界方程为

(40)

Ti=

(41)

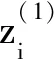
(42)

5.4 1自由度约束的最大公差值求解

若受P方向约束，原T-Map应满足：

(43)

Ti应满足：

(44)

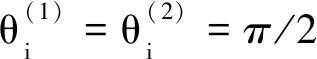
5.5 不同自由度约束下公差转化关系解析

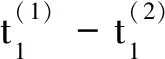
(45)

将式(45)与如下基于特征公差尺寸链的传统公差转化方法中的公差转化关系相比：

(46)

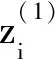
6 实例应用

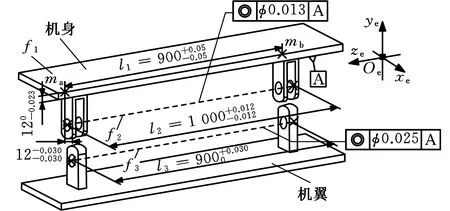
图10 基准变换前的叉耳式飞机机身-机翼 对接简化图Fig.10 Fork-type aircraft fuselage-wing docking simplified diagram before the datum transformation

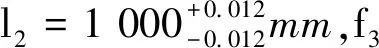
在图10传统装配方案中，通过平面几何特征f1间接传递公差检验l3相对于l2的同轴度，不满足基于点测量布设及测量简单的数字化装配需求。为此，对该方案优化调整，如图11所示。装配基准A的位置用双耳片接头的交点构成的交点轴线替代，同轴度分别为tx和ty。根据图10与图11中的三维尺寸标注信息，将公差转化过程中需要的各参数值统计列于表3。设定如下：基准变换前的装配基准A对应特征，j=1，i=1；基准变换后的装配基准A对应特征，j=2，i=2；目标特征为机翼单耳片接头交点构成的交点轴线，i=3。

图11 基准变换后的叉耳式飞机机身-机翼 对接简化图Fig.11 Fork-type aircraft fuselage-wing docking simplified diagram after the datum transformation表3 公差转化过程中的各参数值Tab.3 The value of each parameter during the tolerance conversion process

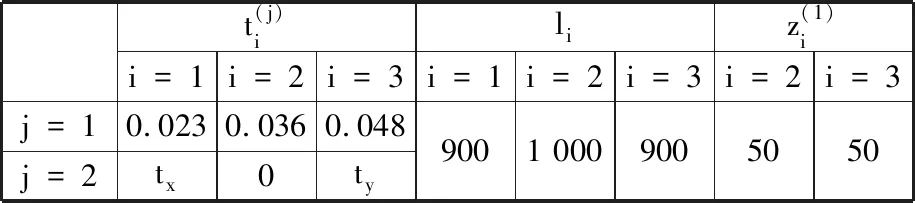
mm

由式(32)和式(45)可得各参数间的约束关系：

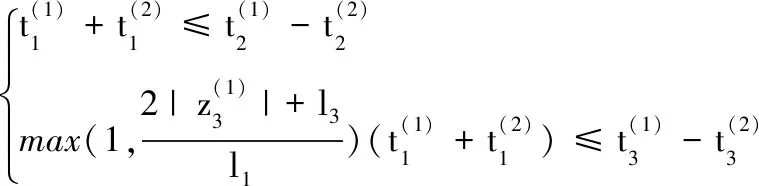
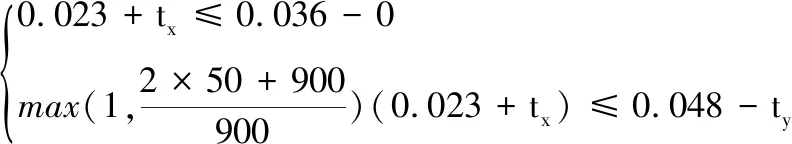
(47)

由式(46)可得各参数间的约束关系：

(48)

对比式(48)、式(47)可知，基于T-Map的公差转化方法相比于基于特征公差尺寸链的公差转化方法，考虑了轴向偏移、理论轴线轴长对转化结果的影响。尺寸链与T-Map公差转化方法得到的同轴度tx与ty关系见图12。

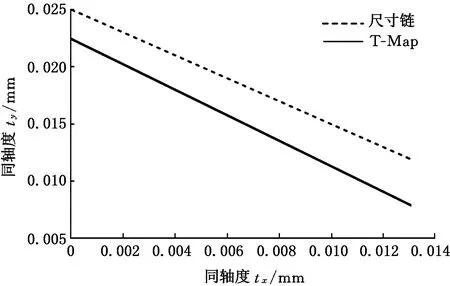
图12 尺寸链与T-Map公差转化方法下同轴度 tx与ty的关系Fig.12 Relationship of concentricity between tx and ty under dimension chain and T-Map tolerance conversion method

由图12可得，基于T-Map的公差转化方法获得的公差值相比于基于特征公差尺寸链的公差转化方法得到的公差值更精确。如，同轴度tx=0.013 mm时，基于T-Map的公差转化方法获得的同轴度(ty=0.008 mm)小于基于特征公差尺寸链的公差转化方法获得的同轴度(ty=0.012 mm)。

7 结论

(1)利用映射点表示装配特征，利用T-Map几何关系表示装配特征变动关系，将装配特征变动转化为T-Map点空间模型的坐标变换，可直接建立装配特征偏差波动的空间域，满足了面向点测量模式的数字化装配容差控制的需求，通过T-Map求解几何公差变动区域与ASME标准对几何公差的定义一致。

(2)将基于T-Map的公差转化方法与传统的尺寸链公差转化方法相比，通过基准变换过程中的几何尺寸及公差关系，建立了面向装配的公差转化关系，通过基准间相互约束的自由度个数，解析了不同自由度方向约束的偏差，从点的坐标值变动层面，对自由度约束的几何公差进行了完整求解，符合三维公差空间特征间的关系，使转化得到的公差值更精确。

(3)本文考虑的几何特征类型单一，还存在一定的局限性，接下来将对基于T-Map的其他特征类型及多基准变换的公差转化方法进行研究。