机械弹性车轮结构参数对汽车侧翻稳定性的影响

李海青 赵又群

南京航空航天大学能源与动力学院，南京，210016

0 引言

汽车行驶的安全性很大程度上依赖于横摆与侧倾稳定性，横摆稳定性的丧失将使汽车失去转向能力或引起汽车的剧烈回转；侧翻稳定性的丧失将引起汽车严重的侧翻事故[1]。汽车失去侧翻稳定性是一种高发并且极具危险的交通事故。侧翻事故的伤害程度仅次于碰撞事故，导致的死亡率高达33%，非碰撞事故中的90%是由汽车侧翻造成的[2]。造成汽车侧翻的原因有两种：一是与行驶中的障碍物侧向撞击引起的绊倒侧翻；二是汽车在紧急避障或换道时产生了很大的侧向加速度，引起很大的侧向载荷转移，当一侧车轮离地时，就可能发生侧翻[3]。重型越野车整车尺寸大、质心较高，更容易发生侧翻事故。

汽车防侧翻技术主要分为被动安全技术和主动安全技术。主动安全技术通过先进的控制技术(如主动制动技术[4-5]、主动转向技术[6-7]、主动悬架技术[8-9]等)提高汽车抗侧翻能力；被动安全技术是在生产研制过程中，通过设计合理的结构参数以提高汽车抗侧翻的能力。ALEKSANDER[10]分析了悬架参数与轮胎受力对车辆侧倾的影响。王国林等[11]研究了轮胎的力学性能和整车操纵稳定性的相互匹配关系，轮胎力学特性与汽车的行驶稳定性是一个相互匹配的关系[12]。汽车失稳的本质原因是轮胎的侧偏特性进入非线性区域，轮胎侧向力发生饱和。影响轮胎侧偏特性的因素较多，主要包括轮胎的结构参数、垂直载荷、胎压、行驶速度、路面状况等。与此同时，普通充气胎存在爆胎等安全隐患，据统计，由轮胎安全隐患引发的严重交通事占比约50%[13]，对汽车行驶安全性产生了较大影响。为克服传统充气胎的不足，课题组提出了一种非充气机械弹性安全车轮，并对车轮的接地特性[14]、静态力学特性[15]、纵向与侧偏力学特性[16-17]、振动特性[18]以及通过性[19]等进行了大量的研究工作。

综合考虑机械弹性车轮(MEW)自身结构特点，通过研究MEW侧偏特性对侧翻稳定性的影响和自身结构参数对其侧偏特性的影响，进而得出MEW结构参数对汽车侧翻稳定性的具体影响规律，为车轮结构优化提供相应的理论基础。

1 汽车侧翻稳定性仿真模型

建立匹配MEW的三自由度(纵向运动、横摆运动、侧倾运动)非线性动力学模型。忽略转向系统的结构影响；忽略车辆纵向车速的变化；不考虑车辆的垂向、俯仰运动；不考虑悬架的非线性，以等效的刚度和阻尼代替。模型的输入信号为前轮转角。以三自由度车辆模型为基础，计算侧翻评价指标所需要的各项参数。

1.1 三自由度整车模型

三自由度整车模型如图1所示。y轴方向的力平衡方程为

(1)

式中，m、ms分别为车辆的总质量、簧载质量；vx、vy分别为车辆的纵向、侧向速度；γ为车辆的横摆角速度；hs为质心位置距侧倾中心的距离；φ为车辆的侧倾角；δf为前轮转角；Fy为车轮的侧向力。

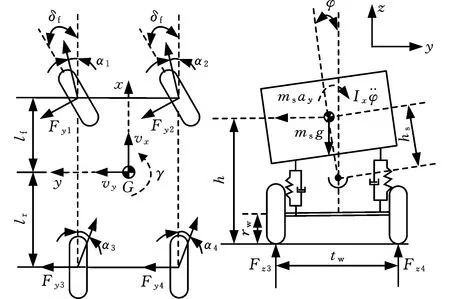
图1 三自由度整车模型示意图Fig.1 3-DOF nonlinear vehicle model

绕z轴的横摆运动方程为

(2)

式中，Iz为簧载质量的横摆转动惯量；lf、lr分别为质心位置到前后轴的距离。

绕x轴的侧倾运动方程为

(3)

Kφ=Kφf+KφrCφ=Cφf+Cφr

式中，Ix为侧倾转动惯量；Kφf、Kφr分别为前后轴悬架的等效侧倾刚度；Cφf、Cφr分别为前后轴悬架的等效阻尼；g为重力加速度。

前后轴车轮的侧偏角为

(4)

式中，tw为轮距。

忽略纵向载荷转移，前后轴各车轮的垂向载荷为

(5)

式中，l为轴距。

1.2 机械弹性车轮力学模型

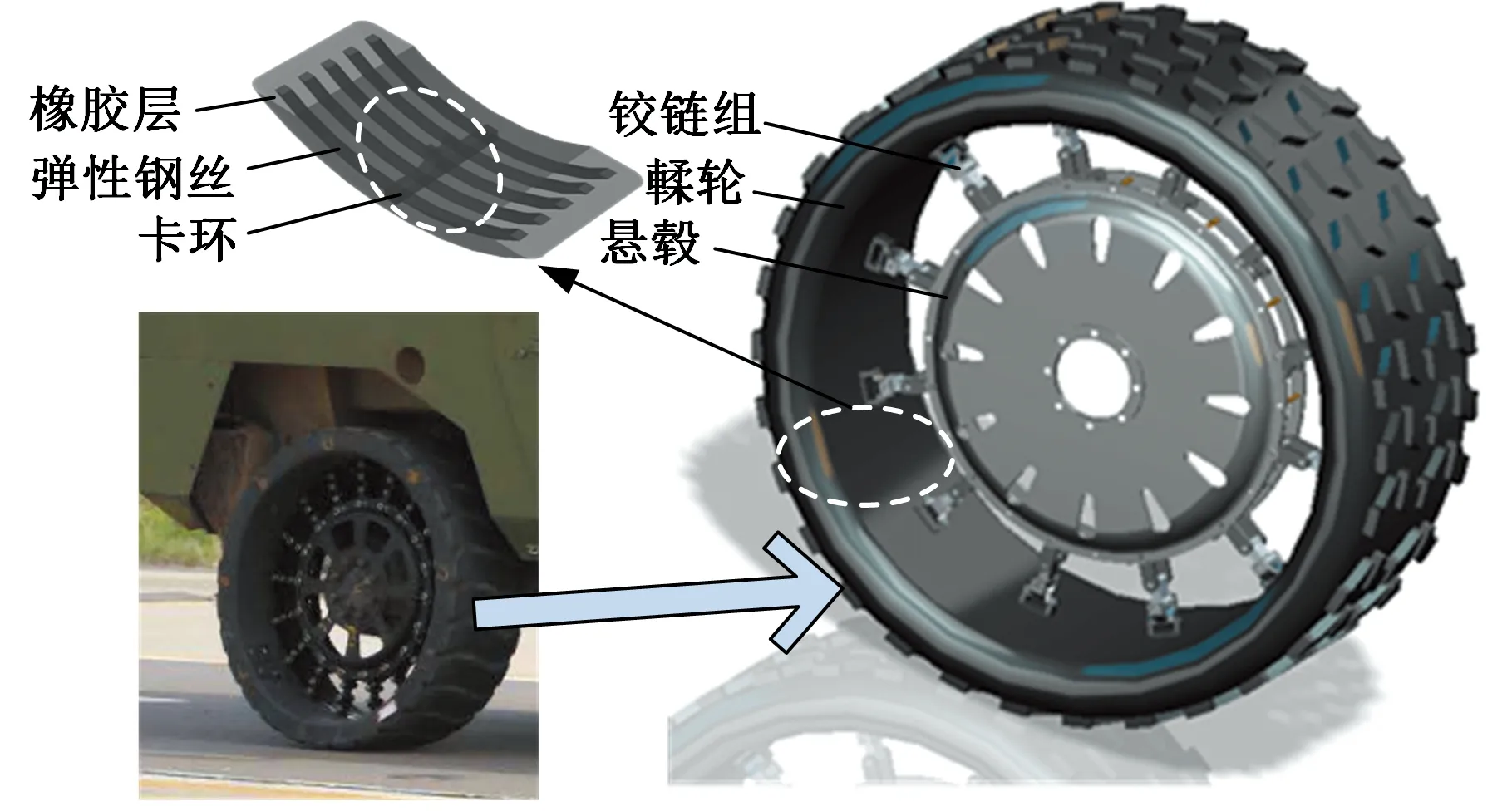
图2 MEW结构示意图Fig.2 Structure of the MEW

MEW是一种新型的非充气安全车轮，其结构见图2。它主要由铰链组、輮轮和悬毂三大部分构成。基于刷子理论模型，在车轮与路面的接地印迹长度为2lp时，以印迹中点为坐标原点建立车轮的垂向及侧向变形示意图，见图3。

图3 车轮载荷分布及侧向变形示意图Fig.3 Tread deformation of the elements in lateral direction

以刷毛单元A-A′为例，当车轮的侧偏角为α时，刷毛单元在Y方向的侧向变形

ζ=(lp-x)tanα

(6)

整个接触区域内刷毛单元侧向形变的单元弹性力

Fey=keyζ=key(lp-x)tanα

(7)

其中，key为车轮的侧向分布刚度。假设车轮在整个接地区域内无滑移，则整个接触区域的侧向力

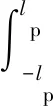
(8)

若附着系数为μ，则每个刷毛单元的最大侧向力满足

Fey≤μFez

(9)

设刷毛单元的垂向分布载荷

(10)

式中，λc为待定常数。

整个印迹内的垂向力

(11)

若垂向力Fz已知,则

(12)

则刷毛单元的最大侧向力

(13)

(14)

整个接地区域内的侧向力

(15)

当xt=lp时，车轮在接地区域全部滑移，设此时的侧偏角为αc，则有tanαc=1/θy；当αc设定时，可求出整个印迹区域内的侧向力：

(16)

由式(16)，每个车轮的侧向力

(17)

i=1,2,3,4

利用平板式轮胎力学特性试验台，对MEW样机进行力学特性试验，其基本结构见图4。利用二次多项式拟合方法，得到车轮接地印迹半长和侧向分布刚度随垂向力的变化关系:

(18)

(19)

其中，参数具体取值见表1。

图4 轮胎力学特性试验台Fig.4 Experimental set-up of tire mechanical characteristics表1 刷子模型拟合参数Tab.1 Fitted coefficient of brush model

a1b1c1a2b2c2-0.043.3949.89-0.0160.493.59

动力机构带动模拟路面以0.3 m/s的平移速度从试验台架一侧移至另一侧，利用建立的刷子模型分析MEW的侧偏力学特性，当Fz=15 kN，μ=0.8，α∈[0, 20°]时,刷子模型的仿真结果和车轮物理样机的试验结果如图5所示。由图5可知，仿真结果与试验结果有较好的一致性。

Study on the suitability evaluation for engineering geological conditions of the underground

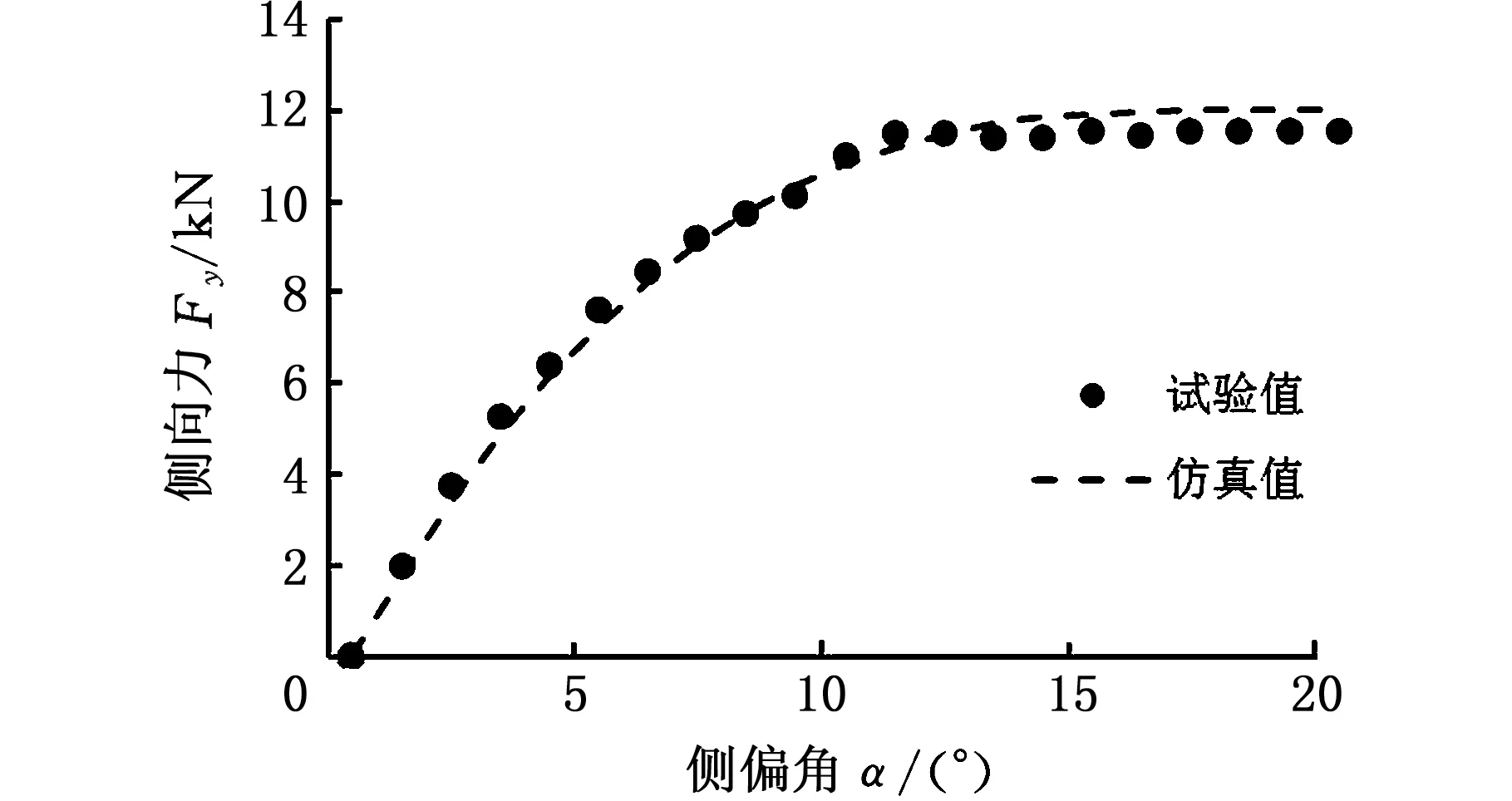
图5 MEW侧偏力学关系曲线Fig.5 Lateral tire force response of MEW

1.3 侧翻预测模型验证

将三自由度模型和CarSim模型进行对比，以某越野车为研究对象，车辆的主要参数见表2。

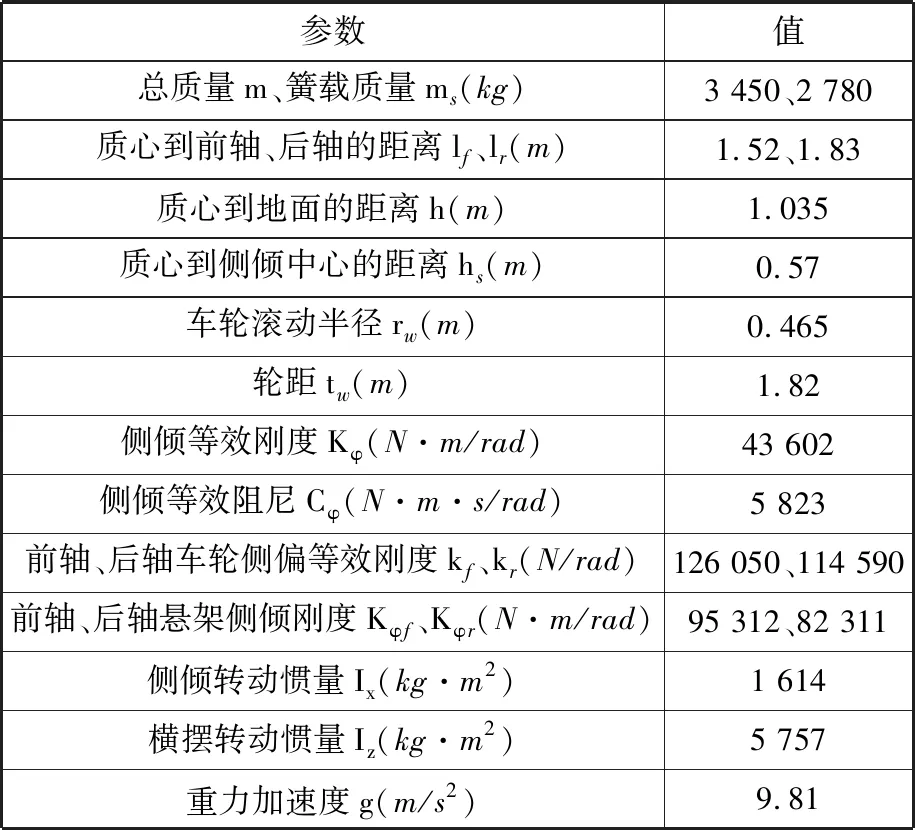
表2 某越野车的主要结构参数Tab.2 Parameters and values for off-road vehicle model

转向盘正弦输入如图6所示，初始车速为60 km/h，μ=0.85，车辆的横摆角速度和侧倾角响应对比如图7所示。

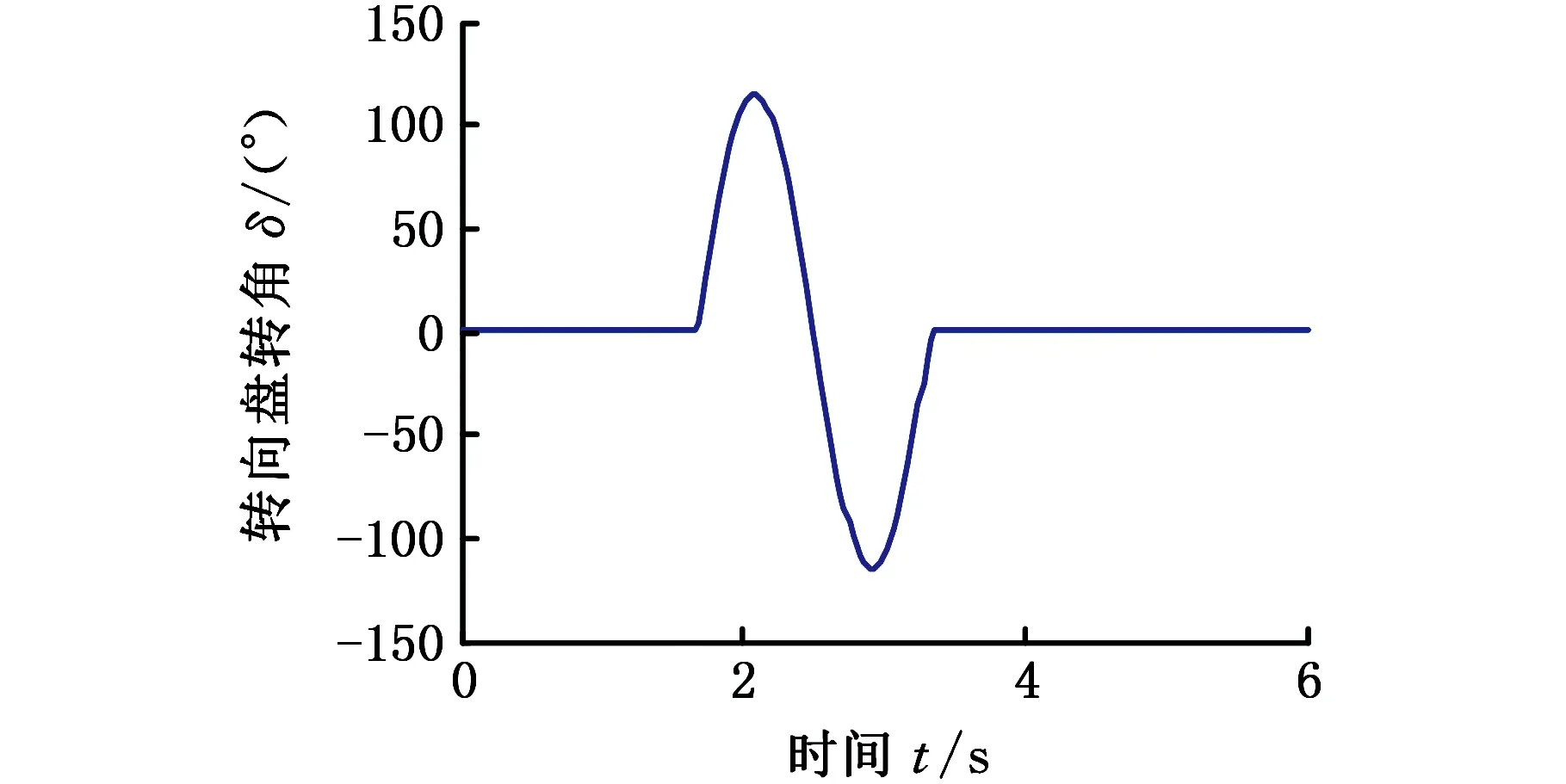
图6 转向盘正弦输入(转向传动比为20)Fig.6 Steering wheel angle sin input (the steering rotation ratio is 20)

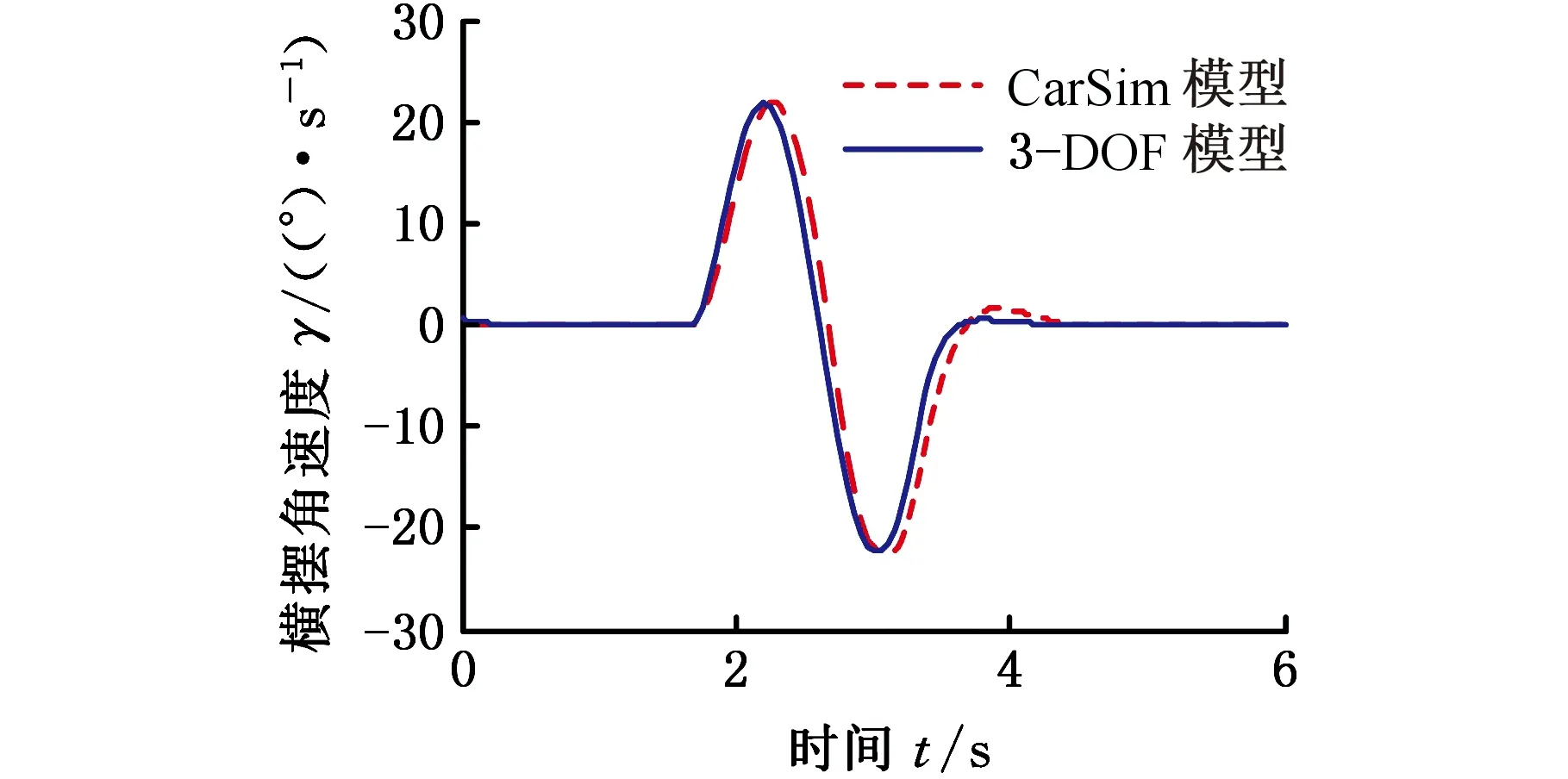
(a)横摆响应

(b)侧倾响应图7 横摆与侧倾响应对比Fig.7 Yaw and rollover response comparison

由图7可知，三自由度仿真模型计算的横摆角速度和侧倾角与CarSim仿真结果差异较小，说明建立的仿真模型能够比较准确地描述车辆的运动。

2 车轮侧偏特性对侧翻稳定性影响

2.1 车轮侧偏特性评价指标

通过充气轮胎与非充气轮胎的轮胎侧偏特性试验数据发现，不同试验状态下，车轮侧向力随侧偏角的变化趋势基本一致。当侧偏角小于5°时，车轮的侧向力随侧偏角线性增大；当侧偏角继续增大时，车轮的侧向力非线性增大直到饱和。提取车轮的侧偏刚度kα、侧向力峰值Fymax作为车轮侧偏特性的评价指标(图8)研究不同侧偏特性的MEW对侧翻稳定性的影响规律。

图8 机械弹性车轮侧偏特性评价指标Fig.8 Evaluation index of the MEW cornering properties

改变车轮的结构参数和材料特性，得到垂向载荷为15 kN时的侧偏刚度kα1～kα3和侧向力峰值Fy1max～Fy3max，如表3所示。

表3 侧偏刚度和侧向力峰值Tab.3 Cornering stiffness and peak value of lateral force

2.2 汽车侧翻稳定性评价指标

研究汽车侧翻预测，首先应从汽车的侧翻稳定机理入手。图9为车辆侧倾时的简化示意图。

图9 汽车侧翻简化模型力学分析Fig.9 Force analysis of vehicle rollover model

对G′点列力矩平衡方程：

(20)

其中，Δy=hsinφ。常用横向载荷转移率(LTR)rLT来预测汽车是否会发生侧翻，其表达式为

(21)

LTR的绝对值越大则表明汽车的侧翻风险越大。将式(20)代入式(21)，假设ms=m，则

(22)

为了验证由式(22)获得LTR估计值的准确性，在CarSim的整车动力学模型中，在转向盘转角信号为正弦输入时，对比LTR估计值与实际值，如图10所示，其中，实际值通过式(21)计算得到，估计值通过式(22)计算得到。CarSim中车辆模型的转向盘转角正弦输入信号同图6。

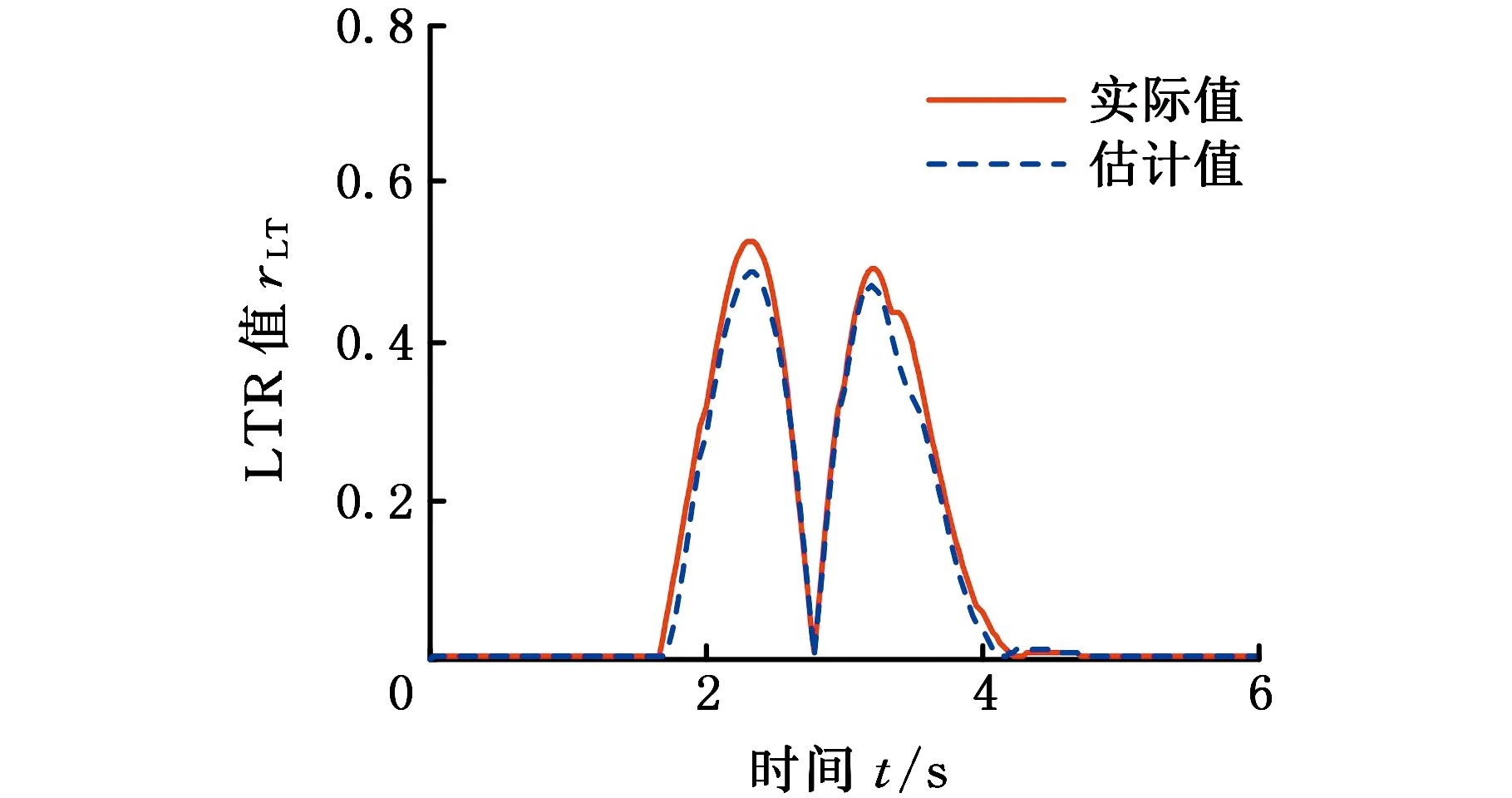
图10 LTR结果对比Fig.10 Result of the LTR comparisons

由图10可以看出，两种计算结果在峰值处最大误差约12%，估计值略小于实际值，其余时刻两者的变化趋势符合较好。

定义预测横向载荷转移率(PLTR)如下：

(23)

其中,Δt为预测时间，t0为当前时间。当侧倾角较小时, 假设sinφ≈φ, 将式(22) 代入式(23),得

(24)

may=-C0β-C1γ/vx+kfδf

(25)

δf=δ/Iβ=vy/vx

C0=kf+krC1=lfkf-lrkr

式中，δ为转向盘转角；I为转向盘传动比。

对式(25)两边求导化简得

(26)

将式(26) 代入式 (24),PLTR的最终表达式为

(27)

为了确定式(27)的预测时间，不同预测时间的侧翻预测指标PLTR估计值如图11所示。预测时间Δt=0时，即为LTR，预测时间Δt=0.1 s时，峰值处的PLTR比LTR大约15%，预测时间Δt=0.2 s时，峰值处的PLTR比LTR大约4%，考虑实际情况，故而取Δt=0.1 s。

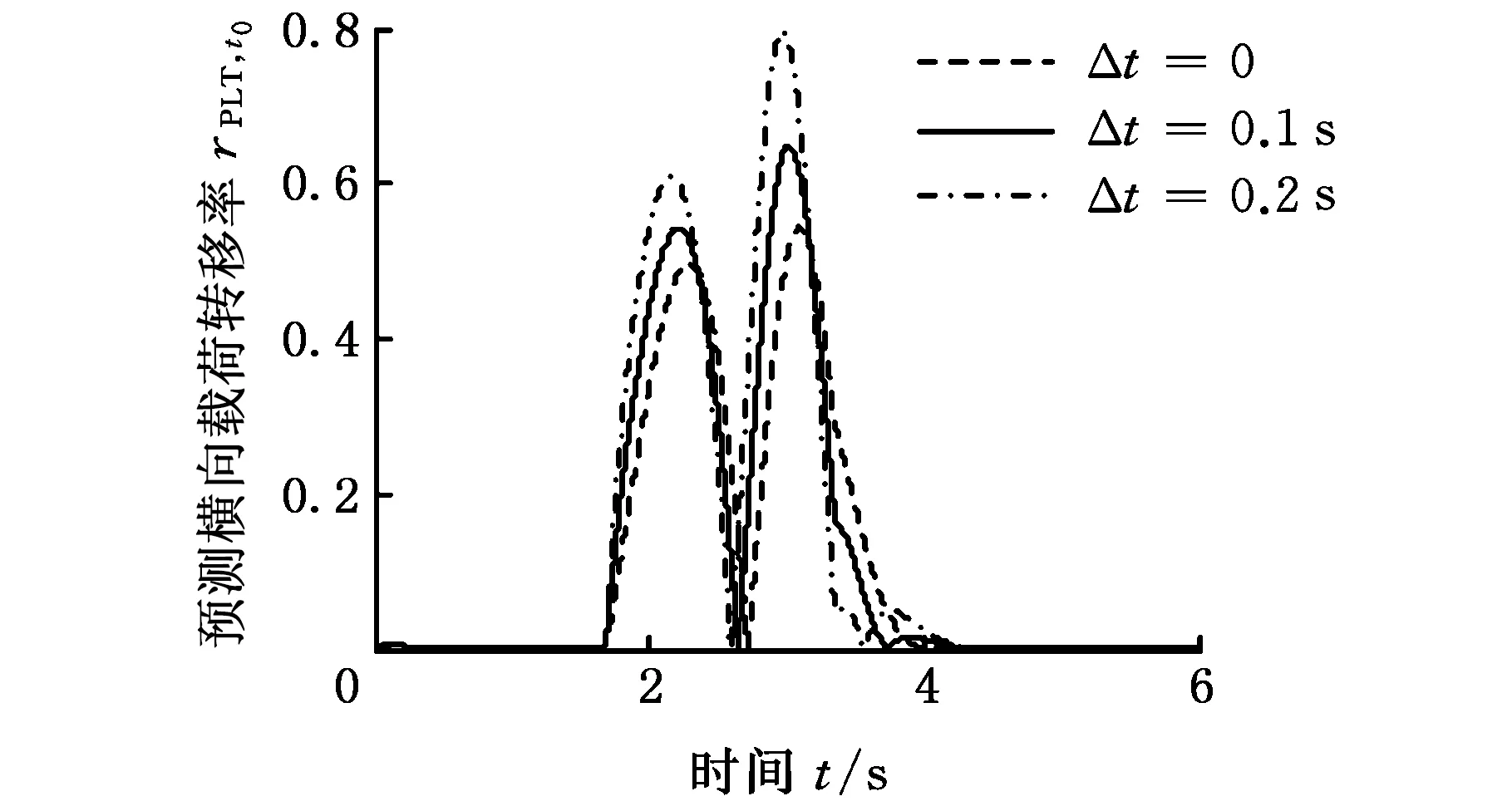
图11 不同预测时间的PLTR结果对比Fig.11 PLTR comparisons by different preview time

2.3 车轮侧偏刚度对侧翻稳定性的影响

将轮胎的侧偏刚度kα在原来的基础上同时增大和减小20%，采用鱼钩试验(图12)仿真工况进行测试，最大转角为288°，初始车速为60 km/h，得到车辆侧倾响应和PLTR的变化曲线，分别见图13、图14。

图12 鱼钩转向试验Fig.12 Steer angle input for Fishhook maneuver

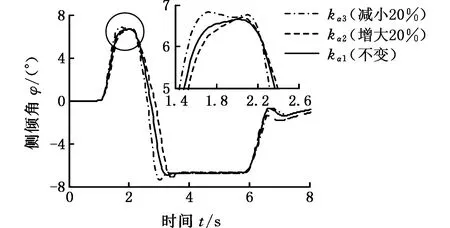
(a)侧倾角

(b)侧倾角-侧倾角速度相平面图13 不同侧偏刚度的侧倾响应对比Fig.13 Roll response comparison at different cornering stiffness

图14 不同侧偏刚度的PLTR对比Fig.14 PLTR comparison at different cornering stiffness

由图13a和图14可知，当车轮的侧偏刚度增大或减小20%时，侧倾角和PLTR的最大值变化并不明显，但侧倾角为6.5°时对应的时刻比原来滞后或者提前了0.1 s，PLTR的值均为0.85时对应的时刻也比原来滞后或提前了0.1 s。由图13b可知，当车轮的侧偏刚度值增大20%时，侧倾角-侧倾角速度相平面图曲线范围变小，变小幅度在3%以内；当车轮的侧偏刚度值减小20%时，侧倾角-侧倾角速度相平面图曲线范围变大，变大幅度在5%以内。由此可知，当侧向力峰值不变时，车轮侧偏刚度对侧翻稳定性影响较小，但对汽车的响应快慢(操控性)影响显著。

2.4 侧向力峰值对侧翻稳定性的影响

将轮胎的侧向力峰值在原来的基础上同时增大或减小20%，保持侧偏刚度不变，得到车辆侧倾响应和PLTR的变化曲线，见图15、图16。

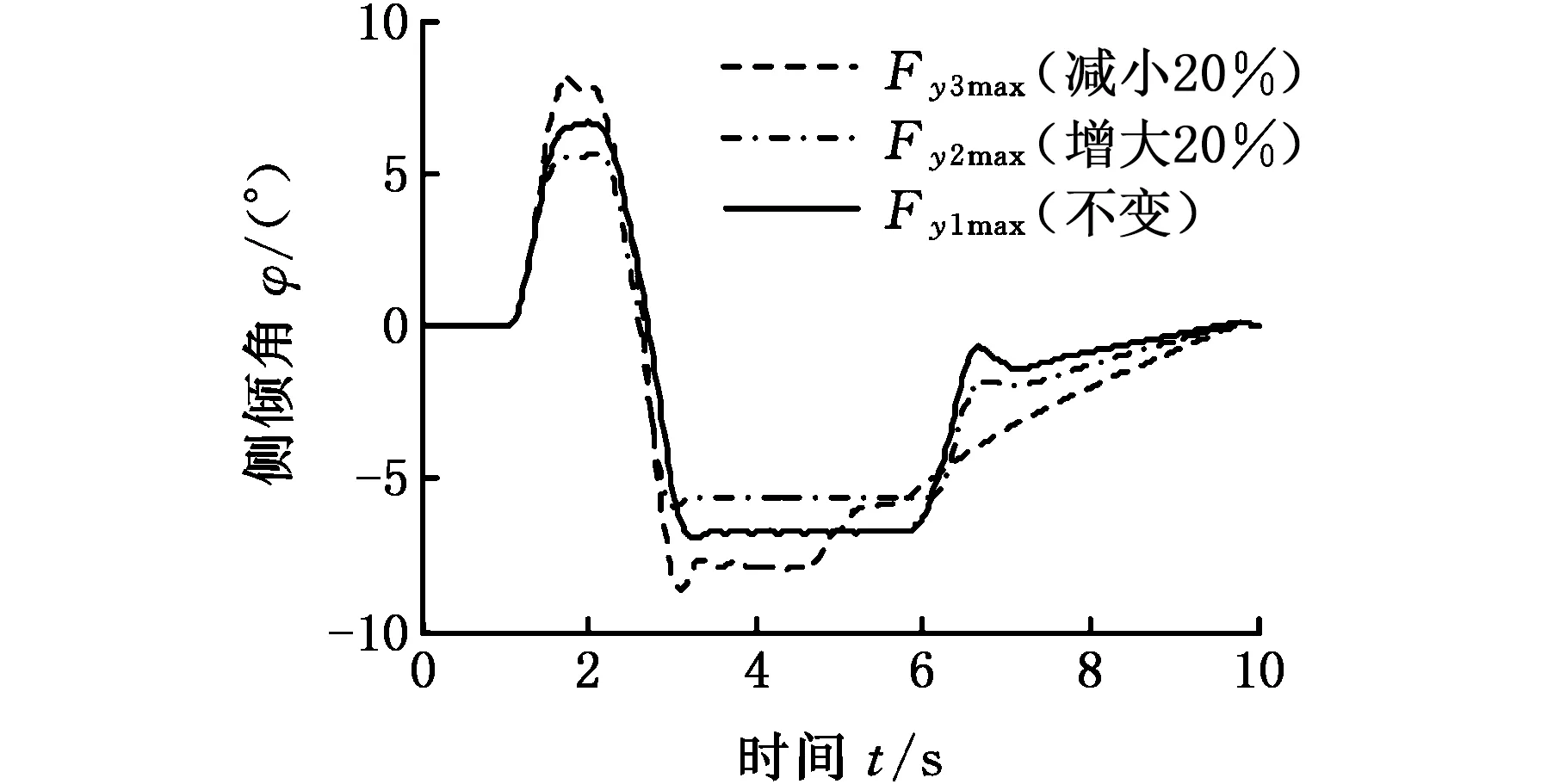
(a)侧倾角

(b)侧倾角-侧倾角速度相平面图15 不同侧向力峰值的侧倾响应对比Fig.15 Roll response comparison at different Fymax

图16 不同侧向力峰值的PLTR对比Fig.16 PLTR comparison at different Fymax

由图15a和图16可知，当侧向力峰值增大20%时，侧倾角最大值由6.8°减小到5.8°；PLTR最大值由0.9减小到0.75；当车轮的侧向力峰值减小20%时，侧偏角最大值由原来的6.8°增加到8.5°，而PLTR最大值由0.9增加到1.1。由图15b可知，当车轮的侧向力峰值增大20%时，侧倾角-侧倾角速度相平面图曲线范围变小，变小幅度超过10%；当车轮的侧向力峰值减小20%时，侧倾角-侧倾角速度相平面图曲线范围变大，变大幅度超过50%。由此可知，当侧偏刚度一定时，随着车轮侧向力峰值的增大，汽车的侧翻稳定性明显增强。

3 车轮结构参数对侧偏特性的影响

3.1 MEW侧偏特性影响因素

MEW承载时的垂向与侧向变形见图17。Fz为车轮所受的垂向载荷，接地区域内，MEW的铰链组因輮轮变形而弯曲，因而不受作用力，其他的铰链组受拉力而张紧。车轮承受侧向力Fy时，因铰链组的侧向刚度相对较大，可近似认为铰链组不发生侧向变形，只有輮轮与路面的接触部分在侧向力的作用下产生侧向变形。以侧向刚度作为MEW静力学侧偏特性的评价指标，研究不同铰链组结构参数(铰链组数目和长度)对车轮侧向刚度的影响。在垂向载荷为15 kN的工况下，对比试验不同铰链组的MEW样机，得到不同铰链组结构参数下的侧向刚度值，如表4所示。

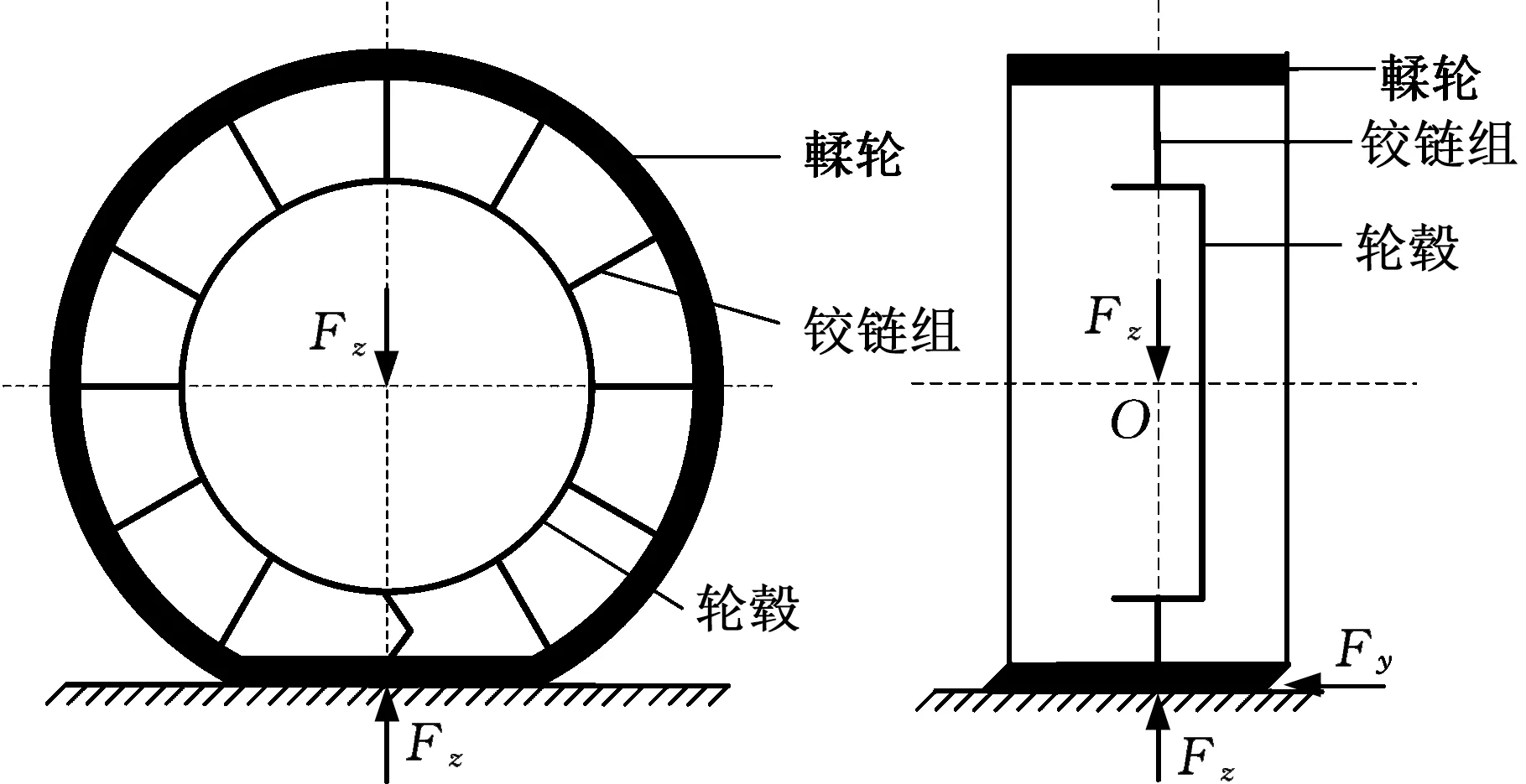
图17 MEW受载荷时的垂向及侧向变形示意图Fig.17 Tread deformation of the MEW in lateral and vertical direction表4 不同铰链组结构参数下的侧向刚度值Tab.4 Lateral stiffness at different parameters of hinge unit

铰链组结构参数长度(mm)数目侧向刚度(N/mm)120122501201825512512235

从表4中可以看出，当铰链组长度不变时，随着车轮铰链组数目的增加，车轮侧向刚度增大2%。在铰链组数目不变的情况下，随着铰链组长度的增大，侧向刚度减小6%。综上可知，铰链组数目及长度对车轮侧向刚度影响较小。为进一步研究车轮与輮轮侧向刚度的相互关系，在垂向载荷为15 kN时，对比輮轮与车轮的侧向刚度特性，结果如图18所示。

图18 輮轮与MEW的侧向刚度特性对比Fig.18 Lateral stiffness comparison of MEW and tire body

从图18中可知，輮轮与车轮的侧向刚度变化趋势基本一致。两者的最大相对误差小于5%。可以近似认为MEW侧向承载变形主要由輮轮实现。

3.2 结构参数对侧偏特性影响分析

在垂向载荷不变的情况下，改变车轮的结构参数，分析结构参数对车轮侧偏特性的具体影响。建立车轮的三维有限元模型，如图19所示。

图19 MEW三维有限元模型Fig.19 Three-dimensional finite element model of MEW

利用有限元分析软件ABAQUS对车轮有限元模型进行侧偏特性仿真试验。假定有限元模型的基本结构尺寸(輮轮外径rw、輮轮断面宽度B)为定值。通过改变輮轮断面高度H，得到不同的輮轮断面高宽比H/B；当H不变时，通过改变弹性环分布高度hd，得到不同的弹性环分布高度系数hd/H；针对不同的H/B、hd/H，将车轮初始模型作相应的结构尺寸修改，得到不同的结构参数试验模型,如表5所示。

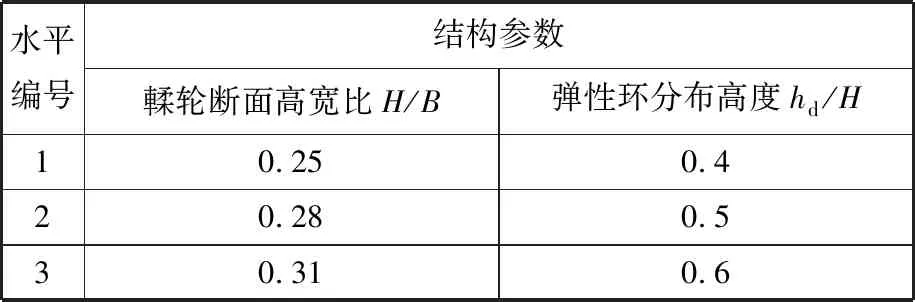
表5 輮轮几何结构参数的水平Tab.5 Geometry parameters of the flexible tire body’s level

为研究橡胶层的初始剪切模量对车轮侧偏特性的影响，利用有限元材料模型辨识工具，设计了不同初始剪切模量：1.04 MPa、1.30 MPa、1.56 MPa。对上述影响因素进行编号，A代表輮轮断面高宽比H/B；B代表弹性环分布高度系数hd/H；C代表橡胶层初始剪切模量。选用L9(33)型正交表，对MEW侧偏特性进行仿真计算，获得不同水平下的车轮侧偏特性评价指标对应的均值，如表6所示。表7为各结构参数不同水平下的侧偏刚度均值，表8为各结构参数不同水平下的侧向力峰值均值。

由表7和表8的数据绘制各结构参数对MEW侧偏特性评价指标的影响趋势曲线，如图20所示。

由图20可知，随着輮轮断面高宽比的增大，车轮的侧偏刚度减小，侧向力峰值变化较小；随着弹性环分布高度的增大，车轮侧偏刚度与侧向力峰值均增大，随着初始剪切模量的增大，车轮侧偏

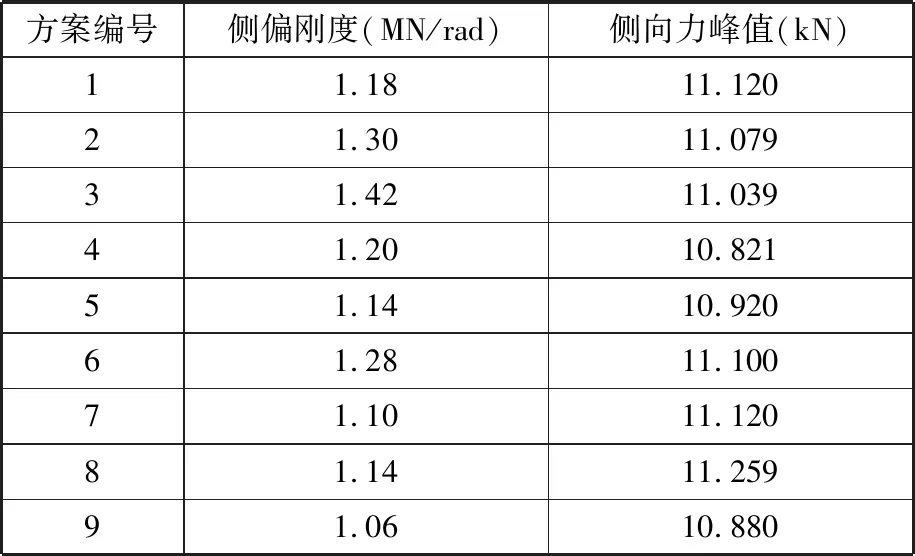
表6 车轮侧偏特性评价指标的计算结果Tab.6 Result of cornering characteristic evaluation index

表7 各结构参数不同水平下的侧偏刚度均值Tab.7 Mean value of cornering stiffness at different levels MN/rad

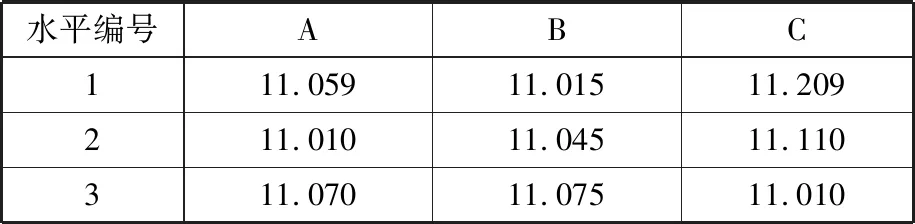
表8 各结构参数不同水平下的侧向力峰值均值Tab.8 Mean peak value of lateral force at different levels kN

(a)侧偏刚度

(b)侧向力峰值图20 侧偏特性随各因素的变化趋势Fig.20 Change trend of cornering properties with various factors

刚度增大，侧向力峰值减小。

综上，增大弹性环分布高度、减小輮轮断面高宽比和初始剪切模量可以增大车轮侧偏刚度和侧向力峰值，提高匹配机械弹性车轮汽车的侧翻稳定性。

4 结论

(1)机械弹性车轮侧向承载变形主要由輮轮实现；减小铰链组长度，增加铰链组数目时，车轮侧向刚度增大，但铰链组数参数对侧向刚度影响较小。

(2)增大輮轮断面高宽比，车轮的侧偏刚度减小，侧向力峰值基本不变；增大弹性环分布高度，车轮的侧偏刚度和侧向力峰值均增大；增大初始剪切模量，车轮的侧偏刚度增大，侧向力峰值减小。

(3)当侧向力峰值一定时，车轮侧偏刚度对汽车的侧翻稳定性影响较小；当侧偏刚度一定时，增大车轮侧向力峰值，汽车的侧翻稳定性明显增强；在满足要求的情况下，应适当增大弹性环分布高度，减小輮轮断面高宽比和初始剪切模量，增加铰链组数目，减小铰链组长度，获得较大侧向力峰值的同时增大车轮的侧偏刚度，进而提高匹配机械弹性车轮汽车的侧翻稳定性。