残余位移反应谱的参数影响研究1

李 宇 梁亚东 李 琛

1）长安大学，公路学院，陕西西安 710064

2）长安大学，建筑学院，陕西西安 710061

引言

强震过后，桥梁残余位移如果较大，将不能继续使用或修复。因此，日本道路协会《桥梁抗震规范》（Japan Road Association，1996）规定进行桥梁抗震设计时，应考虑残余位移的影响。早在20 世纪80 年代，Mahin 等（1981）开始关注结构震后的残余位移，并指出残余位移依赖于结构的恢复力模型。Kawashima 等（1998）和MacRae 等（1997）给出残余位移比的定义，并针对双线性非线性SDOF 体系，计算相应的残余位移反应谱。Zatar 等（2000）指出采用部分预应力混凝土结构替代全预应力混凝土结构或普通钢筋混凝土结构，可有效降低结构的残余位移。李芳宝等（2007）研究近场具有脉冲地层运动的双线性SDOF 体系残余位移比谱。李宇（2010）也提出了考虑残余位移和土-结构相互作用的桥梁结构基于性能的抗震设计及评估方法。李平等（2017）分析软土残余应变的变化规律，并结合地区震陷经验系数，提出软土震陷简化计算方法。杜修力等（2018）研究地震动峰值位移和峰值速度对地下结构地震反应的影响。上述学者虽对残余位移谱进行研究，但所选取的地震动记录较少，所得研究结果并不具有统计意义。因此，本文选取大量强震记录作为输入，针对考虑刚度退化且具有不同周期的非线性单自由度SDOF（SDOF）体系，进行非线性时程分析，以研究地震动特性和恢复力模型参数对残余位移反应谱的影响。

1 基本理论

2 强震记录的选取

周锡元等（2001）对比了中美抗震规范的场地类型，如表1 所示。我国规范的Ⅰ类场地覆盖美国规范的A、B 类和部分C 类场地；我国规范的Ⅱ类场地介于美国规范的C、D 类场地之间；我国规范的Ⅲ类场地介于美国规范的D、E 类场地之间；我国规范的Ⅳ类场地和美国规范的E 类场地接近。

表1 抗震规范场地类别的对比 Table1 Comparison of site conditions

在此基础上，本文从PEER 强震数据库中挑选320 条地震动记录（Ⅰ—Ⅳ类场地各80条，如图1 所示）。通过320 条地震动记录统计的放大系数曲线与规范值吻合较好（中华人民共和国铁道部，2006；中华人民共和国交通运输部，2008），即所选取的地震动记录符合要求，如图2 所示。

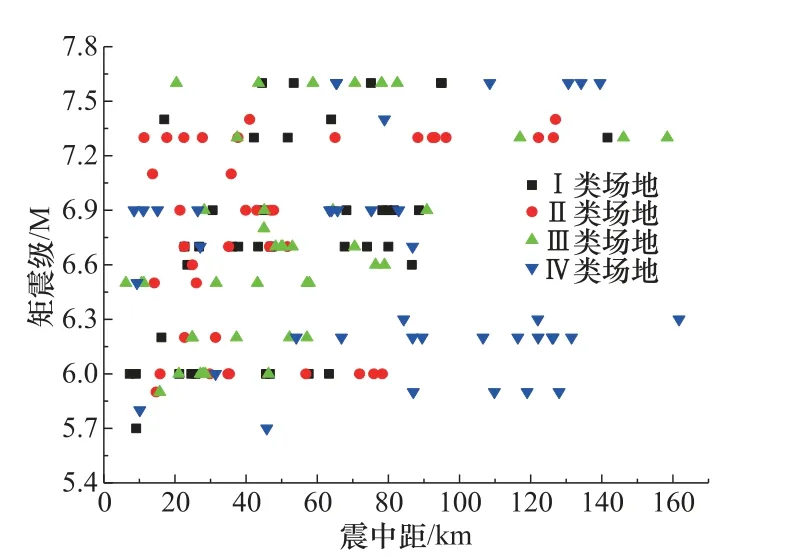
图1 震级-距离分布 Fig.1 Magnitude-distance

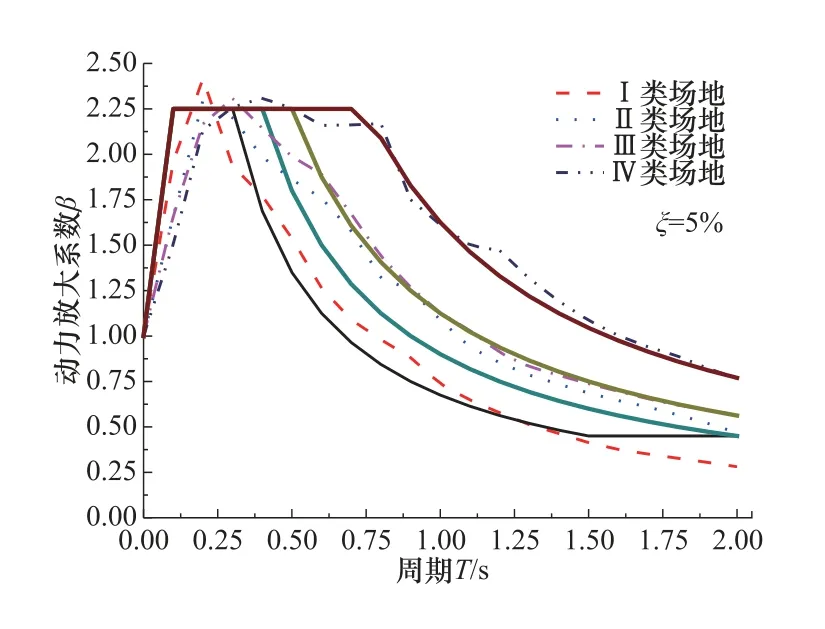
图2 不同场地的动力放大系数 Fig.2 Comparison of β

3 地震动特性对残余位移反应谱的影响

将320 条地震动记录的PGA 调整一致后作为输入，采用Takeda 刚度退化模型，取ξ=5%、η=0.05、μ=1—6，利用BISPEC（Mahmoud，2000）计算T=0.05—5s 的非线性单自由度体系的残余位移的平均值，计算结果如图3 所示。

将320 条地震动记录分为小震（震级为5.7—6.2，100 条）、中震（震级为6.3—6.8，80 条）和大震（震级为6.9—7.6，140 条），由图3（a）可知，当μ相同时，Dres的谱值随震级的增大而增大。这是因为震级越大，地震输入能量越大，非线性SDOF 体系的残余位移相应地增加。

由图3（b）可知，当场地土较硬（Ⅰ、Ⅱ类场地）时，场地类型对Dres的谱值的影响较小；当场地土较软（Ⅲ、Ⅳ类场地）时，Dres的谱值随土质的变软而增大。

由图3（c）可知，Dres的谱值随PGA 增加而增大。另外，若以7 度Dres的谱值为准，其他设防烈度（6、8、9 度）的Dres的谱值为7 度Dres的谱值的0.523、1.810 倍和3.047 倍，这和6、8、9 度的PGA 与7 度的PGA 之比近似，即PGA6度/PGA7度=0.11g/0.21g=0.524，PGA8度/PGA7度=0.38g/0.21g=1.811，PGA9度/PGA7度=0.64g/0.21g=3.048。

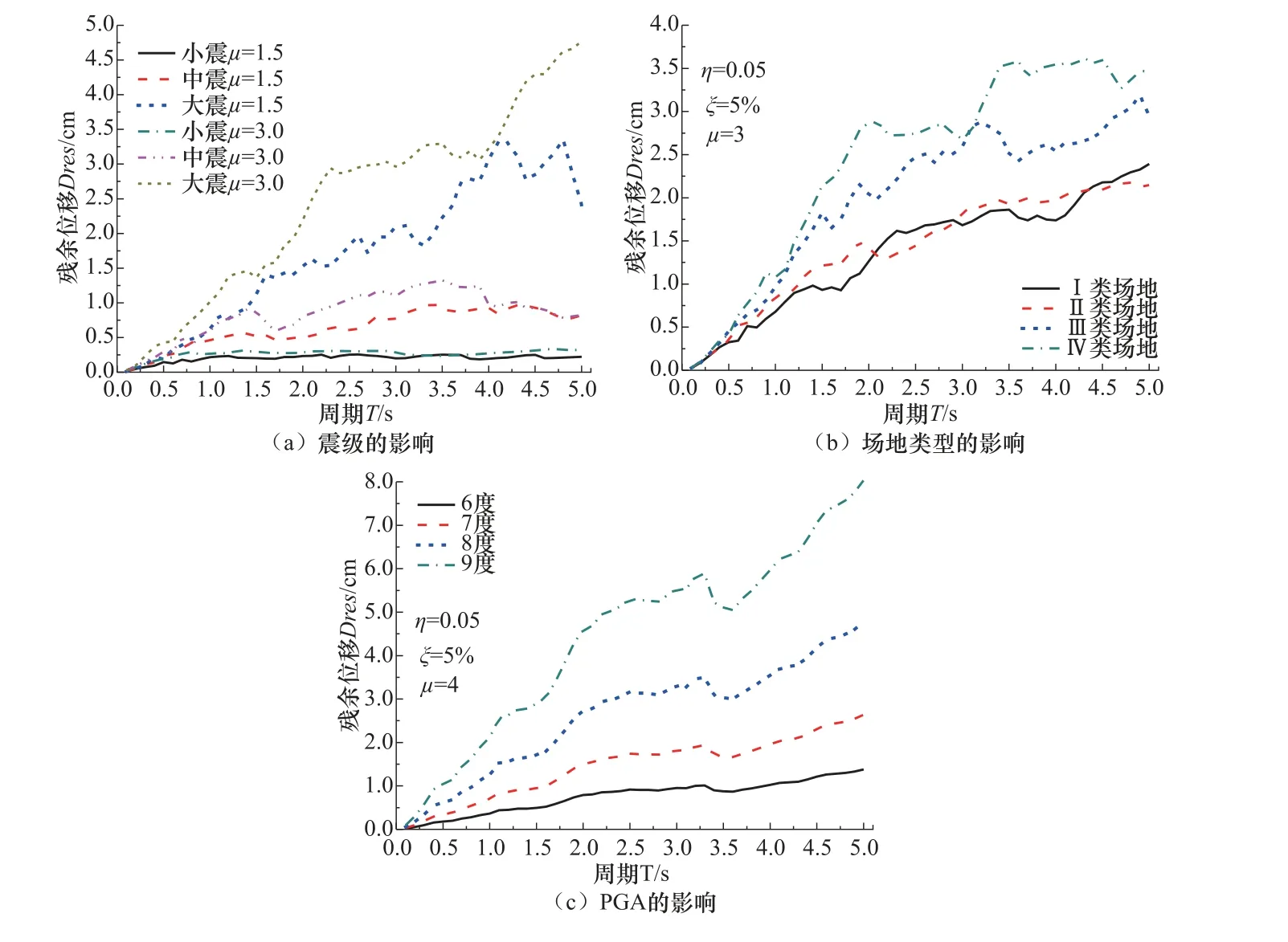
图3 震级、场地土、PGA 对Dres 的影响 Fig.3 Effect of MW，site，PGA on Dres

4 动力参数对残余位移反应谱的影响

以Ⅰ类场地为例，将80 条地震动记录的PGA 调幅为0.21g 后作为输入，利用BISPEC（Mahmoud，2000）计算不同恢复力模型（双线性模型、Takeda 模型）、不同屈服后刚度比（η=0.0、0.025、0.05）、不同阻尼比（ξ=2%、5%、10%、14%）、不同位移延性比（μ=1.0—5.0）等情况下非线性SDOF 体系（T=0.05—5s）残余位移的平均值，计算结果如图4 所示。

图4 动力参数对Dres 的影响（一） Fig.4 Effect of dynamic parameters on Dres

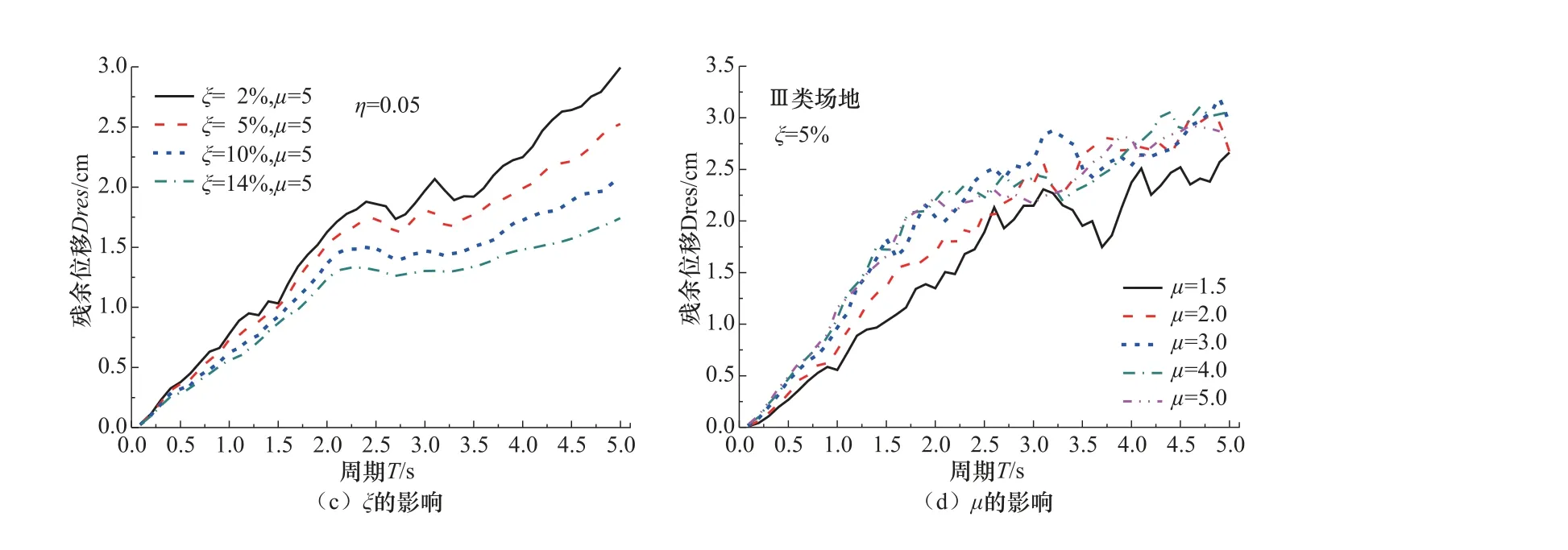
图4 动力参数对Dres 的影响（二） Fig.4 Effect of dynamic parameters on Dres

由图4（a）可知，Takeda 模型Dres的谱值小于双线性模型，其差值随T的增加而加剧，在长周期处尤为明显。由图4（b）可知，当μ较小时，η对Dres的谱值的影响可忽略；但当μ较大时，Dres的谱值随η的增加而减小。由图4（c）可知，随着T的增加，不同ξ对应的Dres的谱值均呈递增趋势。而同一T对应的Dres的谱值则随ξ的增大而减小。可见，ξ的增大会使结构阻尼耗能增加，进而消耗地震能量，以减小结构的残余位移。由图4（d）可知，随着T或μ的增大，Dres的谱值均呈递增趋势。但当μ>3 后，μ对残余位移的影响有所下降。

5 4 类场地残余位移反应谱的统计

将320 条地震动记录的PGA 调幅为0.21g（罕遇地震下7 度设防）后作为输入，采用Takeda模型，取η=0.05、μ=1.25—6.0、ξ=5%，利用BISPEC（Mahmoud，2000）计算4 类场地下非线性SDOF 体系（T=0.05—5s）的残余位移的平均值（其他设防烈度的Dres可由PGA其他与PGA基准之比调整得到）。

图5 4 类场地的Dres（一） Fig.5 Dres of four site

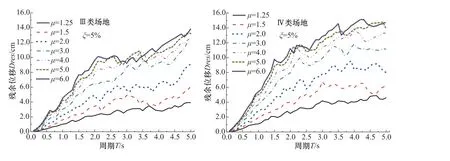
图5 4 类场地的Dres（二） Fig.5 Dres of four site

由如图5 可知，4 类场地的Dres的谱值均随着T或μ的增加而增大；Ⅱ类场地的Dres的谱值最小，其他场地Dres的谱值则随着场地类型的变软而增大。

6 结语

本文通过选取大量地震动记录作为输入，对非线性SDOF 体系的残余位移反应谱进行参数影响研究，得到如下结论：

（1）地震动特性对残余位移反应谱的影响

Dres的谱值随着震级和PGA 的增大而增大；不同设防烈度的Dres可由PGA其他与PGA基准之比调整基准烈度的Dres得到。另外，场地土较硬时，场地类型对Dres的谱值的影响较小；场地土较软时，Dres的谱值随土质的变软而增大；Ⅱ类场地的Dres的谱值最小。

（2）动力参数对残余位移反应谱的影响

Takeda 模型Dres的谱值小于双线性模型，其差值随T的增加而加剧，在长周期处尤为明显；当μ较小时，η对Dres的谱值的影响可忽略，但当μ较大时，Dres的谱值随η的增加而减小；ξ的增大会使结构阻尼耗能增加，进而消耗地震能量，以减小结构的残余位移；随着T或μ的增大，Dres的谱值均呈递增趋势，但当μ>3 后，μ对残余位移的影响有所下降。