钢筋混凝土柱的破坏形态及变形能力研究1

刘 科 黄 娇 马煜东 张 宁 苏佶智

（长安大学建筑工程学院，西安 710061）

引言

基于性能的结构抗震设计克服了目前抗震设计的局限性，是未来抗震设计的发展方向。保证结构在地震作用下的变形需求不超过其变形性能限值是实现基于性能的抗震设计的重要一环。因此，能否准确计算变形性能限值对结构的抗震性能评估结果具有重要的影响。地震作用下，钢筋混凝土（RC）柱是框架结构中的重要受力构件，且容易遭到破坏，从而引起建筑物的倒塌破坏，给生命和财产造成巨大损失。

RC 柱构件在地震作用下由于受力特点和变形能力不同会发生不同类型的破坏，根据构件自身材料特性的不同，常常表现出弯曲破坏、弯剪破坏和剪切破坏三种形态。研究表明，RC 柱的破坏形态不同，其变形性能和延性性能存在较大差异。为了实施基于性能的抗震设计，工程师必须能够根据构件的设计参数或分析参数对构件的破坏形态进行合理的预测。因此，为分析和研究RC 柱的变形能力，首先应对构件的破坏形态进行判别。目前关于RC 柱破坏形态的判别方法主要包括以下几种：（1）基于剪跨比的判别方法，一般认为λ≤ 2构件发生剪切破坏，2 ＜λ＜ 4构件发生弯剪破坏，λ≥ 4构件发生弯曲破坏（万海涛等，2010）；（2）基于试验结果的经验判别方法：主要是根据试验结果中是否出现剪切变形来划分三种破坏形态（Berry，2004）；（3）基于抗剪强度的判别方法：采用45°桁架抗剪模型通过对比抗剪需求与构件的抗剪承载力对破坏形态进行划分（Sezen 等，2004）；而目前关于变形限值的研究有：Maekawa 等（2000）认为影响RC 柱屈服后变形性能的主要因素是剪跨比、轴压比和配箍特征值，并给出考虑这几种因素的位移延性表达式；Elwood 等（2006）提出RC 柱的理想位移角骨架模型用来描述弯曲屈服、剪切破坏及轴向破坏3 个关键破坏特征点，并采用该模型计算框架振动台试验RC 柱特征点的位移角；戚永乐（2012）利用有限元分析，提出基于统一的材料应变限值的RC 梁、柱及剪力墙构件的位移角限值等。

给出RC 柱破坏形态的判别条件是得出其变形性能指标的第一步，准确计算RC 柱的变形性能限值，对实现RC 结构的抗震性能设计具有重要意义。而目前对于破坏形态的判别条件，方法（1）虽然简单实用，但准确率过低；方法（2）缺乏预判性，不能直接用于性能设计；方法（3）将在文中进行验证。当RC 柱处于复杂受力状态时，目前已有的位移角计算公式可能产生较大误差，且存在参数较多，计算过于繁琐等缺点。本文将采用性能设计的方法对RC 柱的变形性能进行研究，首先利用收集的试验数据提出RC 柱不同破坏形态下的判别条件，选择位移角作为柱构件的变形性能指标，进行了轴压比、剪跨比、配箍特征值等参数对位移角的显著性影响分析，回归分析出屈服位移角和极限位移角的经验公式，对RC 柱的变形性能进行了量化1。

1 破坏形态分析

本文从美国太平洋地震研究中心（Pacific Earthquake Engineering，简称PEER）柱数据库中收集了81 根弯曲破坏柱、26 根弯剪破坏柱和16 根剪切破坏柱的抗震性能试验数据，如表1 所示。所有试验数据均含有完整的滞回曲线和骨架曲线，柱试件的剪跨比、轴压比、纵筋配筋率和体积配箍率的分布结果如图1 所示。

对收集的试验数据进行筛选和处理，按式（1）将国外试验数据中混凝土强度设计值fc、标准值fck（棱柱体轴心抗压强度）和标准立方体抗压强度fcu进行换算；按式（2）将混凝土圆柱体抗压强度fc′换算为混凝土轴心受压标准值fck。

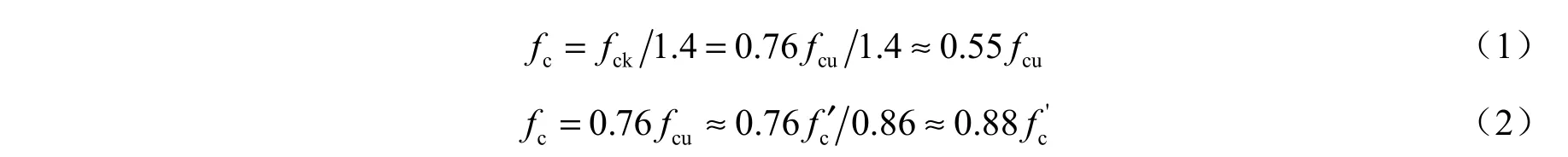
利用收集到的数据对基于抗剪强度的判别方法进行验证，在美国的《混凝土抗震规范》（ASCE/SEI 41—06，2007）中，研究者估算构件的抗剪承载力通常采用Sezen 和Moehle 提出的45°桁架抗剪模型，并通过比较抗剪需求Vp（抗弯强度对应的剪力）和折减后的抗剪承载力Vn进行破坏形态的划分，划分标准如表1 所示。

表1 ASCE/SEI 41-06 标准中的柱破坏模式划分 Table 1 Column failure mode division in ASCE/SEI 41-06

图1 柱试件参数分布直方图 Fig.1 Column test piece parameter distribution histogram

表中，Vp为抗剪需求；Vn为折减后的抗剪承载力，Vp和Vn分别按下式（3）和（4）进行计算：

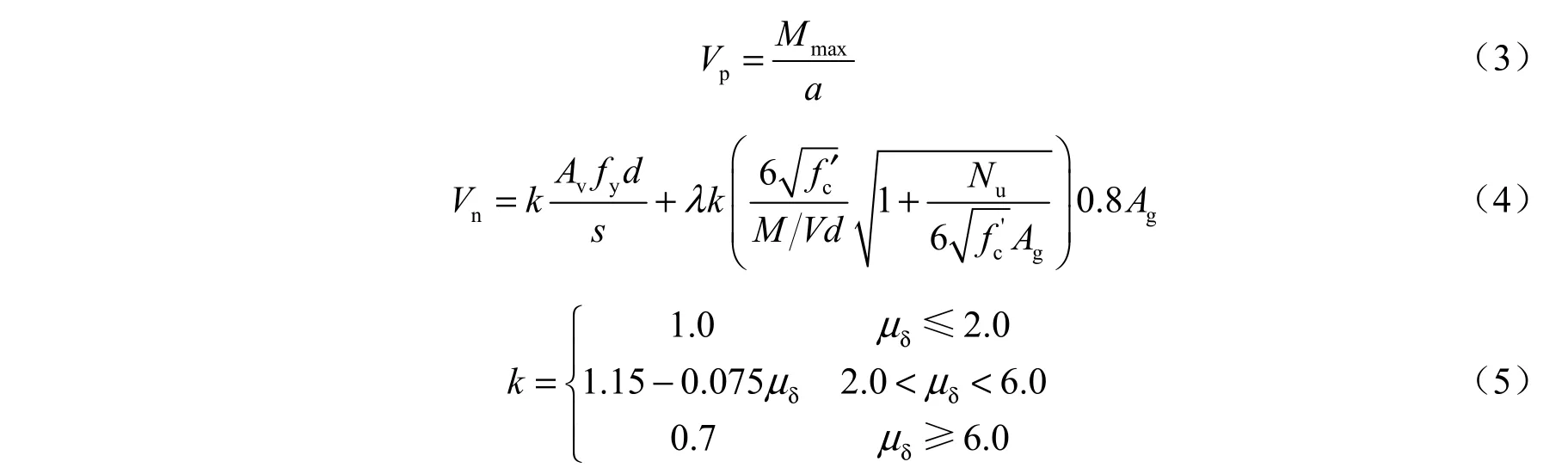
式中，Mmax为最大抗弯承载力；fc′为凝土圆柱体抗压强度；k为凝土抗剪强度折减因子；μδ为移延性；Nu为压力（当受压时=0）；Ag为毛截面面积；Av为筋总截面面积；fy为筋屈服强度；d为构件有效高度；S为剪钢筋的垂直间距；M/Vd＞4 时取4，小于2 时取2。

本文通过收集到的试验数据对上述判别方法的有效性和准确性进行验证，根据柱构件截面 的弯矩-曲率关系计算得到最大抗弯承载力Mmax，抗剪需求Vp和折减后的抗剪承载力Vn通过上述理论公式（3）和（4）计算得出，利用Vp和Vn进一步计算出折减后的弯剪比，根据Vp/(Vn/k)的计算结果和界限值，可以得出破坏形态与Vp/(Vn/k)的关系，如图2 所示。

由图2 可知，弯曲破坏和弯剪破坏的试验数据基于上述判别标准具有较大的离散性，判别标准的3 个区段之间均分布有 弯曲破坏和弯剪破坏的Vp/(Vn/k)，并且有较多重叠的部分，弯曲破坏发生的概率随着弯剪比Vp/(Vn/k)的增大变得越来越小，而弯剪破坏发生的概率则变得越来越大，因 而 以Vp/(Vn/k) = 1.0和Vp/(Vn/k) =0.6为界限也不能够对RC 柱的破坏形态进行准确区分。

2 破坏形态判别

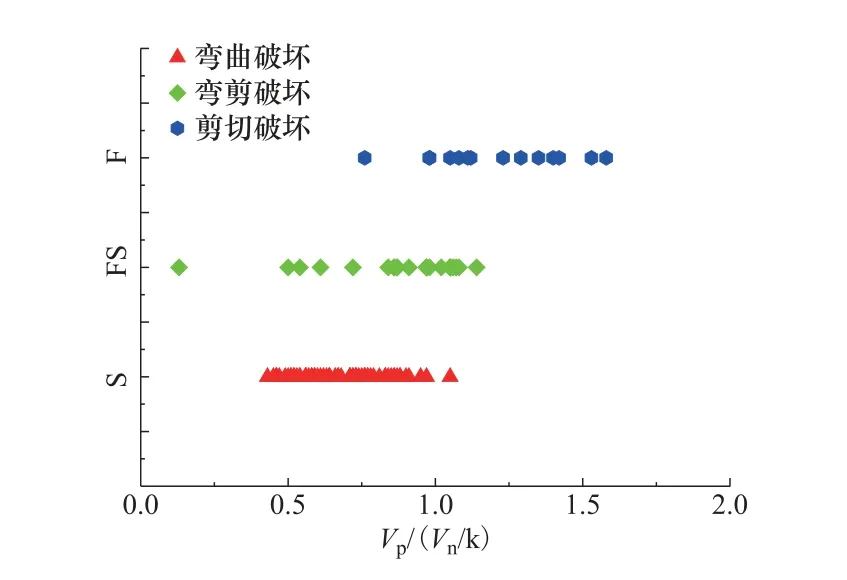
图2 破坏形态与 Vp (V n k )的关系 Fig.2 Relationship between failure form and Vp (V n k )

2.1 破坏形态影响因素

框架结构中的RC 柱受到压力、弯矩和剪力的共同作用，所以构件的正截面承载力和抗剪承载力影响其最终的破坏形态，由《混凝土结构设计规范》GB 50010—2010 可知，对称配筋的RC 柱，其抗压承载力、抗弯承载力和抗剪承载力的计算公式如下。

通过分析上述的计算式可知，纵筋配筋率、纵筋屈服强度、混凝土抗压强度和截面尺寸对RC 柱的正截面承载力有影响，而配箍率、箍筋屈服强度、混凝土抗拉强度以及截面尺寸对RC 柱的抗剪承载力有影响，因而设计参数共同影响着构件的最终破坏形态，同时剪跨比也会对剪切破坏有影响。这些设计参数之间相互影响、相互作用，当这些参数的组合方式不同时，构件可能会发生不同形态的破坏。

2.2 基于参数的破坏形态判别

为了对破坏形态进行更加准确的分类，本文需要根据破坏形态与各影响因素之间的关系提出一种基于参数的破坏形态划分标准。由于柱构件的破坏形态与剪跨比、弯剪比、体积配箍率和纵筋配筋率均有关系，因此本文结合收集到的试验数据可以得到破坏形态与任意两个参数之间的关系，如图3 和表2 所示。

图3 破坏形态与弯剪比和剪跨比的关系 Fig.3 Relationship between Failure Mode and Bending-shear Ratio and Shear-to-span Ratio

表2 破坏形态与剪跨比和配箍特征值、体积配箍率、配筋率之间的关系 Table 2 Relationship between failure mode and shear span ratio and hoop characteristic value, volume hoop ratio and reinforcement ratio

表3 钢筋混凝土柱破坏形态判别标准 Table 3 Discrimination criteria for failure mode of reinforced concrete columns

依据表3 的分类标准，结合收集的试验数据发现，弯曲破坏柱的试验数据符合上述分类标准占比76%，剪切破坏柱的试验数据符合上述分类标准占比95%，而弯剪破坏柱的试验数据符合上述分类标准占比78%。由图3 可知，剪跨比为3，弯剪比为1 附近的弯曲破坏和弯剪破坏的数据重合较多，因此，弯曲破坏柱和弯剪破坏柱的误判可能性稍大，分别为24%和22%。由于弯剪破坏兼具弯曲破坏和剪切破坏的某些特征，RC 柱的弯曲破坏与弯剪破坏、弯剪破坏与剪切破坏之间本身存在难以严格区分的特性，要找到一组百分之百准确区分RC 柱的弯曲、弯剪及剪切破坏形态的参数十分困难。综上，本文所提出基于参数的破坏形态判别标准具有一定的合理性和准确性。

3 变形限值计算分析

国内外对RC 柱进行了大量研究（刘良林等，2016；苏佶智等，2018；董正方等，2010；Ahani 等，2019），但研究者大多主要关注承载力等因素（杨君，2007；李强等，2015；蒋友宝等，2017），本文采用基于性能设计方法，对柱本身的变形性能进行深入研究。常见的衡量构件变形的指标有位移角、塑性区转角及弦转角等，本文选择位移角作为柱构件的变形性能 指标。假设三种破坏状态下的位移角θi与轴压比n、剪跨比λ、配箍特征值βv、体积配箍率ρv和纵筋配筋率ρ均存在线性关系，即位移角θi与各影响因素的线性关系如式（9）所示。

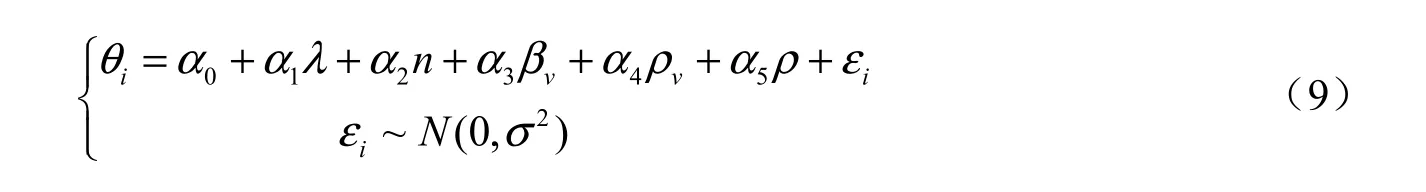
3.1 线性相关分析

线性相关分析是研究两个变量之间线性关系密切程度的一种常用统计方法（Lee 等，2014），描述这种线性关系和方向的统计量称为相关系数r。本文采用Spearman 相关系数r，r位于-1 和1 之间，当r＞0 ，表明两个变量为正相关，当r＜ 0，为负相关。一般情况下，|r| ＞0.8 表示两个变量高度相关，当|r| ＜0.3 时，表示两个变量不相关。

为计算简便，本文利用SPSS 软件对三种破坏形态下的各影响因素与屈服位移角和极限位移角进行Spearman 相关性分析，相关系数分析结果如表4 和表5 所示。

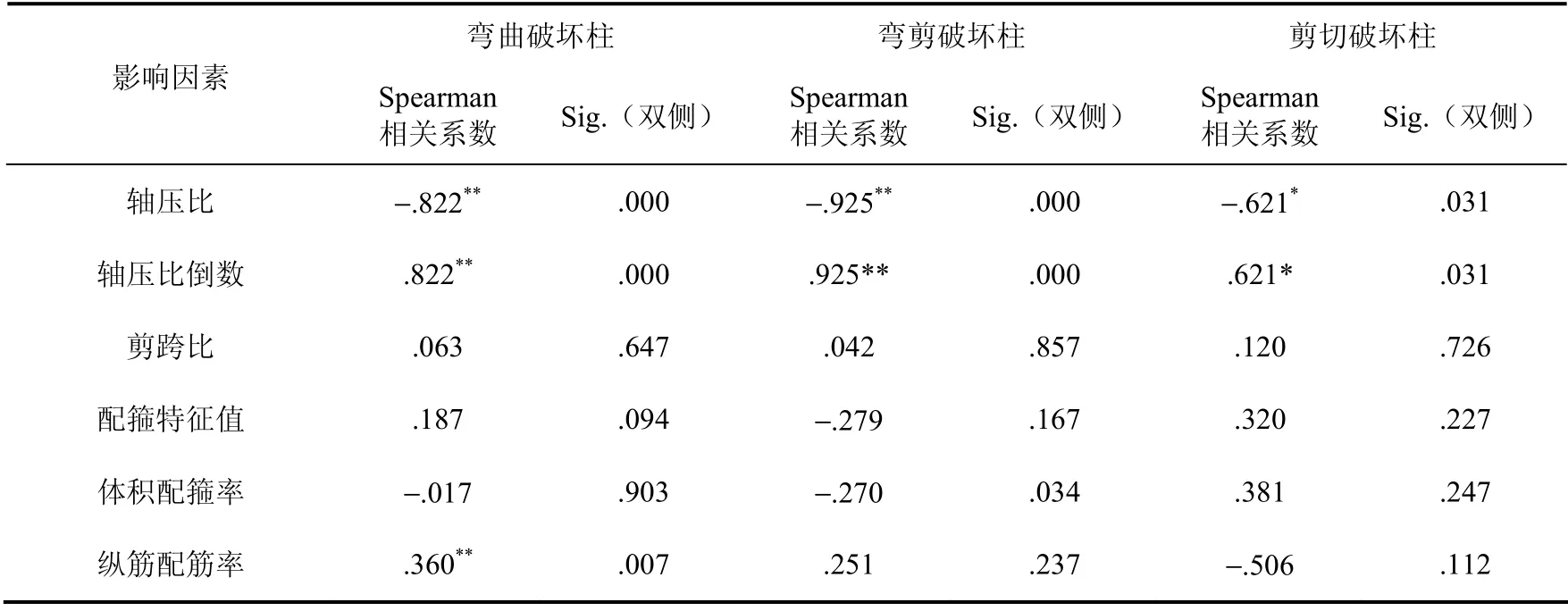
表4 各影响因素与屈服位移角的相关系数 Table 4 Correlation coefficients between various influencing factors and yield displacement angle

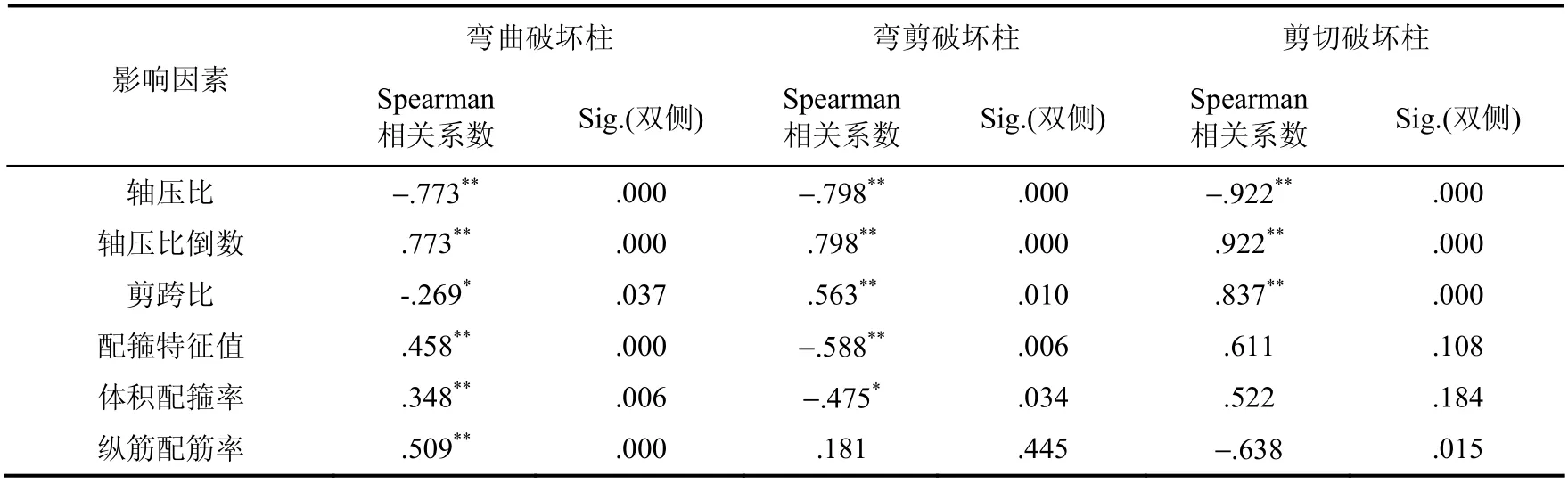
表5 各影响因素与极限位移角的相关系数 Table 5 Correlation coefficients between various influencing factors and ultimate displacement angle

由表4 和表5 可知，RC 柱的屈服位移角θy在弯曲、弯剪、剪切3 种破坏形态下，与轴压比n、配筋率ρ的相关系数较其他因素偏大，且与n为负相关，与ρ为正相关。RC 柱的极限位移角θu在弯曲破坏状态下，与轴压比n、配箍特征值βv、纵筋配筋率ρ相关系数分别为r=-.77**、Sig.=0.00，r=.46**、Sig.=0.00，r=.51**、Sig.=0.00，表明θu与这3 个变量间呈现出较强的线性关系，且与n为负相关，与βv、ρ均为正相关；在弯剪破坏状态下，θu与轴压比n、剪跨比λ、配箍特征值βv相关系数分别为r=−.80**、Sig.=0.00，r=.56**、Sig.=0.01，r=−.59**、Sig.=0.01，表明θu与这3 个变量间呈现出较强的线性关系，且与n、β v均为负相关，与λ为正相关；在剪切破坏状态下，θu与轴压比n、剪跨比λ、纵筋配筋率ρ相关系数分别为r=-.99**、Sig.=0.00，r=.84**、Sig.=0.00，r=-.64**、Sig.=0.02，表明θu与这三个变量间呈现出较强的线性关系，且与n，ρ均为负相关，与λ为呈正相关。

3.2 位移角回归分析

基于以上显著性分析，轴压比n、剪跨比λ、配箍特征值βv、体积配箍率ρv和纵筋配筋率ρ这5 个参数与θy、θu均具有很大相关性，本文分别建立以下破坏状态下RC 柱的回归公式：3种破坏状态下θy与n和ρ为控制参数的公式；弯曲破坏状态下的θu与n、βv和ρ为控制参数的公式；弯剪破坏状态下的θu与n，β v和λ为控制参数的公式；剪切破坏状态下的θu与n、λ和ρ为控制参数的公式。利用SPSS 软件进行线性回归分析最终得到RC 柱的回归方程，如表6 所示。

表6 不同破坏形态下位移角的回归方程 Table 6 Regression equations of displacement angles under different failure modes

屈服位移角和极限位移角在三种破坏状态下回归方程的R、R2和AdjustedR2，如表7 所示。其中，R是相关系数，R2是回归方程拟合优度的度量，取值范围是（0，1），R2越接近1表示回归模型拟合效果越好，AdjustedR2是消除了变量个数影响的R2修正值。

表7 不同破坏形态下位移角回归方程中的R，R2 和Adjusted R2 Table 7 Correlation Coefficients R, R2 and Adjusted R2 in the Displacement Angle Regression Equation under Different Failure Modes

通过表7 可以看出，屈服位移角和极限位移角在三种破坏状态下回归方程的R2和AdjustedR2的值均在0.75 以上，说明拟合效果较好，并采用回归系数T检验回归方程式的显著性概率，即检验回归系数的显著性。

4 结论

（1）本文利用收集到的123 根RC 柱抗震性能试验数据，对现有RC 柱的破坏形态判别标准进行分析，并根据破坏形态和各影响因素之间的关系提出基于剪跨比和弯剪比的破坏形态判别标准，经验证具有一定的合理性。

（2）轴压比和配筋率是影响各破坏状态下屈服位移角θy的主要因素。轴压比、配箍特征值和配筋率是影响弯曲破坏状态下极限位移角θu的主要因素；轴压比、配箍率和剪跨比是影响弯剪破坏状态下θu的主要因素；轴压比、剪跨比和配筋率是影响剪切破坏状态下θu的主要因素。

（3）利用SPSS 软件进行了轴压比、剪跨比、配箍特征值等参数对位移角的显著性影响分析，通过回归分析归纳出位移角的经验公式，并对回归系数进行显著性检验，显著性概率Sig.均小于0.05，表明回归方程具有一定的准确性，为RC 结构抗震性能设计和评估提供了理论依据。