离散Fréchet 距离在强震台站场地 分类中的应用1

梁基冠 程 印 赵 岑

（西南交通大学，土木工程学院，成都 610031）

引言

在地震工程中，强震台站的场地分类具有重要意义，合理地划分强震台站的场地类别为进一步应用强震数据奠定基础（王珊等，2014）。采用合适的指标和适当的方法划定强震台站场地类别是地震工程中的一项重要课题。获取台站钻孔资料时，利用钻孔资料计算相应参数，并将这些参数与各类指标进行比对便可划分场地类别（中华人民共和国住房和城乡建设部等，2010；Building Seismic Safety Council，2003；Ministry of Land，Infrastructure，Transport and Tourism，2007；蒋其峰等，2017）。

无法获取场地钻孔资料时，可用谱比法等经验方法对场地进行大致分类（Borcherdt，1970；Zhao 等，2006；Wen 等，2011；温瑞智等，2015）。经典谱比法需参考场地（Borcherdt，1970），由于参考场地选取不便，有研究者提出无需参考场地的方法，如Nakamura（1989）将横竖向地脉动的傅里叶谱相比以识别场地特性；Lermo 等（1993）、Yamazaki 等（1997）将该方法运用到强震台站场地分类中；Zhao 等（2006）使用5%阻尼比下的横竖向加速度反应谱比进行场地分类，利用阻尼比产生的“一致”平滑效果，避免傅里叶谱平滑操作带来的影响；Fukushima 等（2007）将Zhao 等（2006）的方法应用于建立地震动衰减关系，认为用该方法划分场地类别可降低衰减关系的标准差，表明使用谱比法划分场地类别具有独特的合理性和适用性。利用横竖向反应谱比法对场地进行分类，关键在于将待分类场地的平均反应谱比曲线与各类场地的标准反应谱比曲线相匹配，不同的匹配方法对最终分类结果有很大影响（Zhao 等，2006；Ghasemi 等，2009；Wen 等，2011；温瑞智等，2015；赵万松，2017）。因此，对现有匹配方法进行改进，以期达到更好的分类效果是当前使用谱比法进行场地分类研究的热点问题。利用待分类场地谱比曲线与标准谱比曲线之间的相似性可对场地进行分类。Fréchet 距离是一种判别2 条曲线相似性的工具（Alt 等，1995），两曲线间的Fréchet 距离越小则越相似。Alt 等（1995）提出计算两多边形链的连续Fréchet 距离算法；Eiter 等（1994）提出两多边形链的离散Fréchet 距离算法，并认为离散Fréchet 距离可作为连续Fréchet 距离的近似；Eiter 等（1994）提出的“耦联法”具有概念明确、计算效率高等特点，因而本文采用该方法计算离散Fréchet 距离，并以此为基础进行场地分类。

首先基于《建筑抗震设计规范（GB 50011—2010）》对从日本KiK-net 强震台网获取的664 个具有钻孔资料的强震台站进行场地分类，构建2 个数据集，并求得数据集中各条记录的横竖向反应谱比。在此基础上，计算数据集1 中各类场地的标准谱比曲线和数据集2 中的各台站平均谱比曲线。最后，基于离散Fréchet 距离重新划分数据集2 中各台站的场地类别，并统计此方法分类结果，通过与斯皮尔曼秩相关系数法进行对比，并将应用本文方法分类得到的平均谱比曲线与标准谱比曲线进行对比，以校验本文分类方法的合理性。

1 离散Fréchet 距离

离散Fréchet 距离是连续Fréchet 距离的一种近似，用多边形链近似代替曲线，通过计算两多边形链间的Fréchet 距离，并以此作为两曲线间Fréchet 距离的近似。根据Eiter 等（1994）提出的“耦联法”，在某种情况下将两多边形链P、Q的节点连接起来（即速度组合）：

2 KiK-net 台站标准谱比曲线

2.1 Kik-net 台站场地分类

《建筑抗震设计规范（GB 50011—2010）》使用“双指标”划分场地类别，即由场地覆盖层厚度和等效剪切波速共同决定场地类别。《建筑抗震设计规范（GB 50011—2010）》中，I类场地被划分为I0和I1两个亚类，为保证数据量足够多，本文将二者合为I 类。

日本KiK-net 强震台网由692 个台站组成，分布在日本各地，各台站均有深达基岩的钻孔数据（钻孔深100m 左右）。各台站均由2 组三分量加速度计组成，分布于地表及孔底（Okada等，2004）。自台网运行以来，收集到大量地震动数据，对研究场地效应、地震动衰减模型等具有重要意义。按照《建筑抗震设计规范（GB 50011—2010）》中场地分类方法，对664 个KiK-net 台站进行场地划分，分类结果如表1 所示，台站分布如图2 所示。由于IV 类场地数量较少且《建筑抗震设计规范（GB 50011—2010）》中IV 类场地基本为深软场地，我国强震台站处于该类场地的可能性较小（温瑞智等，2015），本文只制作I、II、III 类场地标准谱比曲线。

表1 KiK-net 台站场地分类结果 Table1 Classification result of KiK-net stations

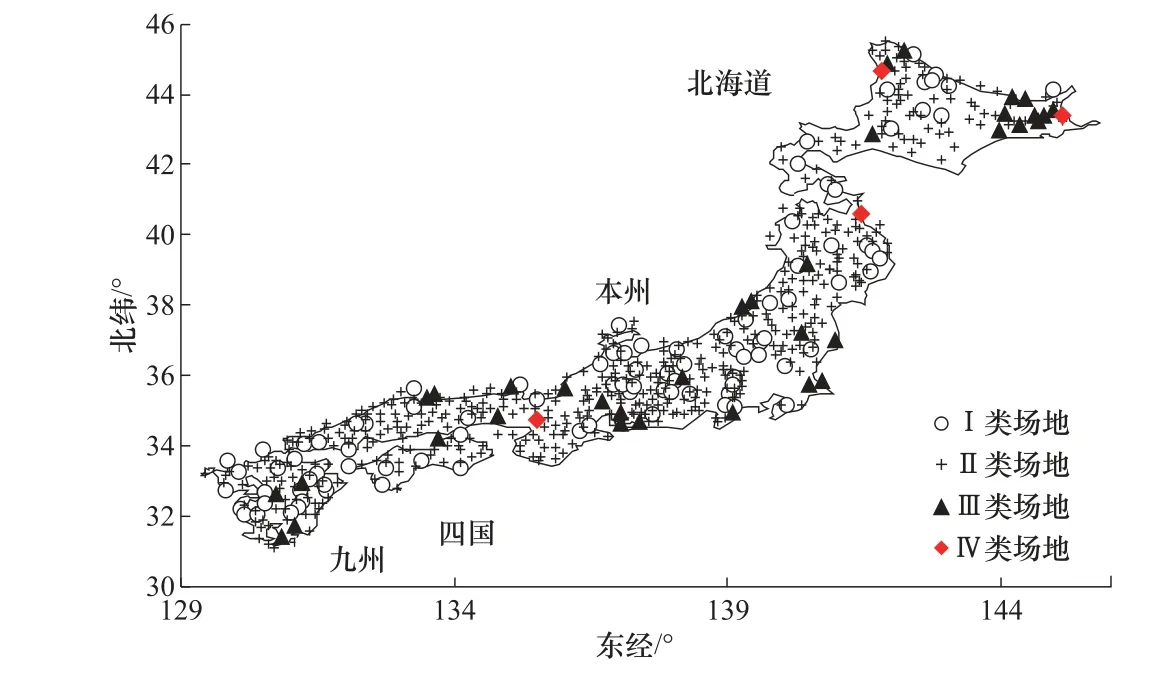
图2 Kik-net 台站场地类别及分布 Fig.2 Site class and distribution of Kik-net stations

在I、II、III 类场地台站中随机选定数据集1 的台站，剩下的台站归入数据集2。数据集1 选取大部分台站，用于获取对应场地类别的标准横竖向反应谱比曲线；数据集2 用于计算所选台站的平均横竖向反应谱比曲线，并利用本文分类方法重新划分台站场地类别，如表2所示。

表2 地震动记录选取信息 Table2 Details on ground motion record selection

2.2 标准谱比曲线

分别计算数据集1 中每条地震动记录3 个分量5%阻尼比下的加速度反应谱，对2 个水平分量的反应谱值进行几何平均，再将几何平均值与竖向反应谱值相比，即可获得单条记录的谱比曲线。对于某一类场地，将该类场地上所有的横竖向反应谱比曲线求几何平均，可得到该类场地标准谱比曲线。对数据集1 中的地震动记录进行计算，得到I、II、III 类场地标准谱比曲线及自然对数标准差曲线，如图3 所示。Zhao 等（2006）及其他研究者（Ghasemi 等，2009）的研究均表明，不同震级、距离下的谱比曲线区别不大，因此谱比曲线主要反映场地效应。由图3（a）可知，I 类场地标准谱比曲线在反应谱周期为0.1 s 时达到最大值，最大值为2.4 左右，峰值区为0.07—0.12 s，整体趋势为先升后降；II 类场地标准谱比曲线在反应谱周期为0.2s 时达到峰值，峰值为2.5 左右，峰值区为0.15—0.25s，整体趋势也为先升后降；III 类场地标准谱比曲线有2 个峰值区，第1 个峰值区为反应谱周期0.12s 附近，第2 个峰值区为0.4—1.05s，峰值为2.8 左右，III 类场地峰值区范围较I、II 类场地广，III 类场地标准谱比曲线最大值出现在反应谱周期为0.5s 时。总体上，本文得到的3 条标准谱比曲线具有良好的区分度。由图3（b）可知，本文得到的3 类场地标准谱比曲线自然对数标准差为0.36—0.60，且随着周期的增加，各类场地自然对 数标准差逐渐稳定，其范围与其他研究者的结果较为接近（Zhao 等，2006；Ghasemi 等，2009；温瑞智等，2015）。因此，本文所得的标准谱比曲线及其自然对数标准差具有合理性。

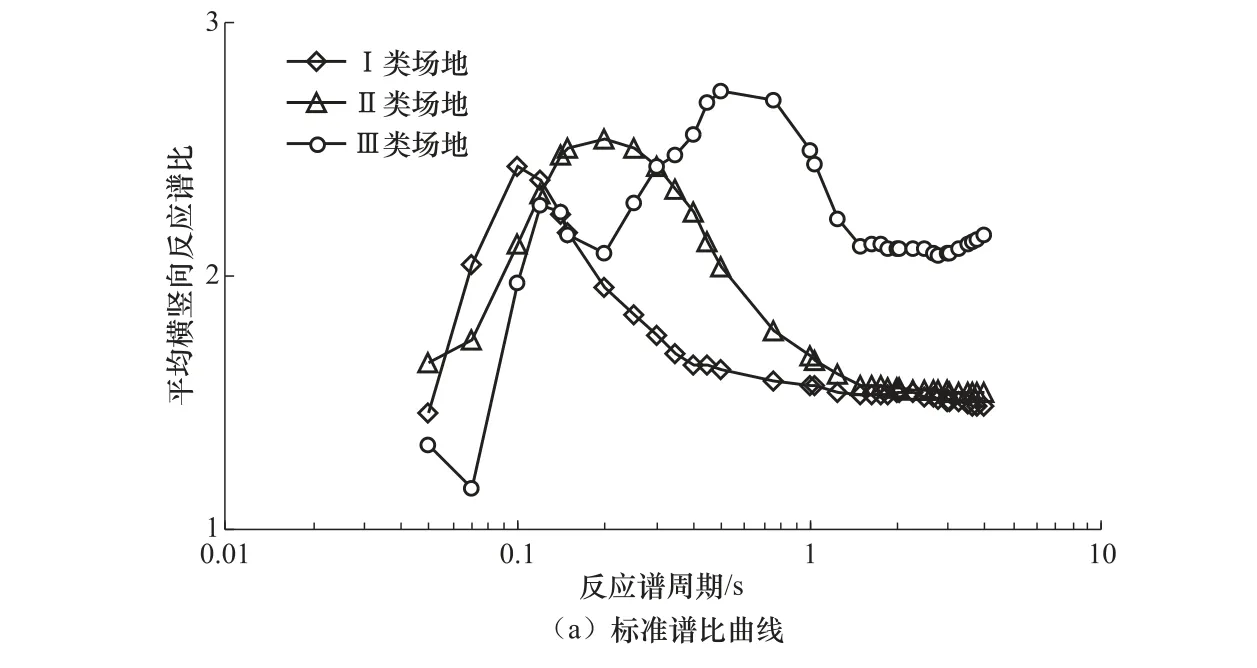
图3 3 类场地标准谱比曲线及其自然对数标准差曲线 Fig.3 Standard spectra ratio curves and natural logarithmic standard deviation for three site classses

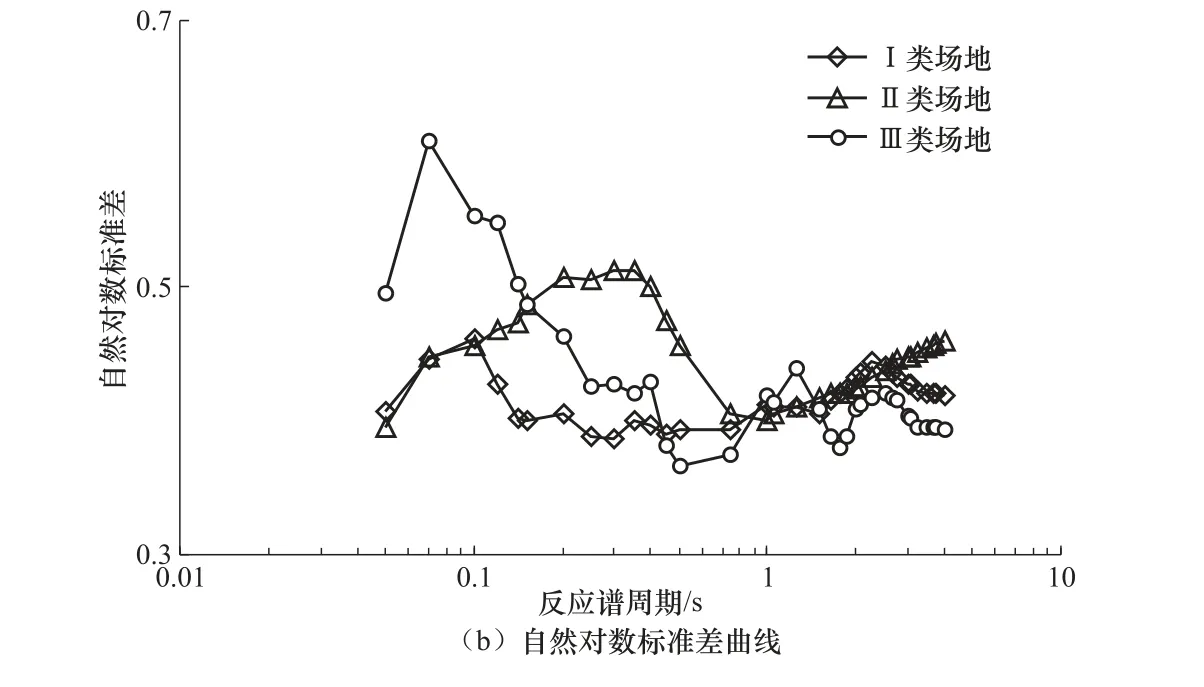
图3 3 类场地标准谱比曲线及其自然对数标准差曲线 Fig.3 Standard spectra ratio curves and natural logarithmic standard deviation for three site classses

3 场地分类结果与校验

3.1 场地划分算例

根据离散Fréchet 距离概念及算法，结合本文得到的3 条标准谱比曲线划分场地类别。本例选用KiK-net 台站KGWH03 钻孔信息，根据《建筑抗震设计规范（GB 50011—2010）》，由钻孔信息划分场地类别，结果如表3 所示。

表3 KGWH03 场地钻孔及场地分类 Table3 Boring Information and Site Classification of KGWH03

使用本文方法对KGWH03 进行场地划分，结果如图4 所示。由图4 可知，场地KGWH03平均横竖向反应谱比曲线总体上较为平坦，在0.07s 附近达到峰值，然后逐渐下降，0.1s 后的下降趋势基本与I 类场地平均谱比曲线一致。KGWH03 谱比曲线在0.1s 时出现凹陷，主要由该场地的数据分布造成。此外，单个场地与整类场地的数据量差异也是造成凹陷的原因之一。II 类场地标准谱比曲线峰值出现在0.2s，整个曲线的形状与KGWH03 平均谱比曲线差异较大。而III 类场地标准谱比曲线具有2 个峰值，下降段斜率更大，与KGWH03 平均谱比曲线差异明显。总的来说，KGWH03 平均谱比曲线与I 类场地标准谱比曲线最为相似。算得KGWH03 平均谱比曲线与I、II、III 类场地离散Fréchet 距离分别为0.777、0.923、1.321（见图4），因此可将KGWH03 划分为I 类场地。由本例可知，谱比曲线间的相似度越高，离散Fréchet 距离越小，利用Fréchet 距离可较合理地划分场地类别。需注意的是，本例中KGWH03平均谱比曲线与3 条标准谱比曲线的离散Fréchet 距离恰好为标准谱比曲线峰值与对应周期上平均谱比曲线的差值，但对于其他台站可能并非如此，须根据“耦联法”计算结果具体分析。

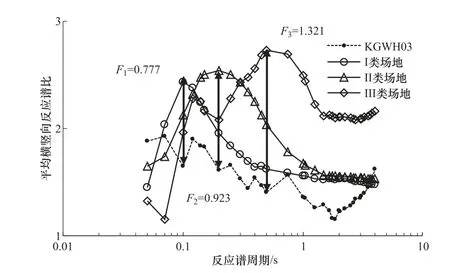
图4 离散Fréchet 距离场地分类算例 Fig.4 Site classifications using discrete Fréchet distance

3.2 场地划分结果对比

式中di为第i个反应谱周期处待分类场地平均谱比曲线与标准谱比曲线间的差；n为反应谱所用周期点数。ρ越接近1 表示两曲线越相似。

使用本文基于离散Fréchet 距离的场地分类方法及斯皮尔曼秩相关系数法分别对数据集2 中的场地进行分类，统计分类成功率及误判率，结果如图5 所示。当本文方法将数据集2 中的I、II、III 类场地重新划分为I、II、III 类时即为成功，否则为失败。图5 中，横坐标“II 类场地”表示重新对数据集2 中的场地进行分类，最终结果显示为II 类场地的部分。

由图5 可知，使用本文方法时，I 类场地成功率为56.00%，低于斯皮尔曼秩相关系数法所得68.00%的成功率。本文方法P12=24.00%，P13=20.00%；而斯皮尔曼秩相关系数法P12=24.00%，P13=8.00%。可知本文方法将I 类场地误判为II、III 类场地的概率接近，而斯皮尔曼秩相关系数法主要将I 类场地划分为I、II 类场地。造成此种差异的原因为本文数据集中I 类场地平均谱比曲线受数据量不足的影响，其形状与I 类场地标准谱比曲线差异较明显，某些场地的平均谱比曲线可能凹凸较多，其与I 类场地标准谱比曲线的离散Fréchet 距离大于II、III 类场地，造成误判。而斯皮尔曼秩相关系数法则是对2 条曲线间的差值求和，一般来说I类场地平均谱比曲线的值均小于I 类场地标准谱比曲线的值，而II、III 类场地标准谱比曲线的值则比I 类场地标准谱比曲线的值大，所以更易区分。对于II 类场地，斯皮尔曼秩相关系数法划分成功率为39.39%，小于本文方法，且斯皮尔曼秩相关系数法P23=42.42%，即成功率与误判率接近，说明斯皮尔曼秩相关系数法难以准确区分II、III 类场地；而本文方法则不然，不仅划分成功率较高，且误判率和成功率之间的差异也较大，即误判风险较小。对于III类场地，本文方法划分成功率为75.00%，大于斯皮尔曼秩相关系数法，说明本文方法在对III类场地的划分上较优。因此，本文方法总体表现较好，具有一定合理性。

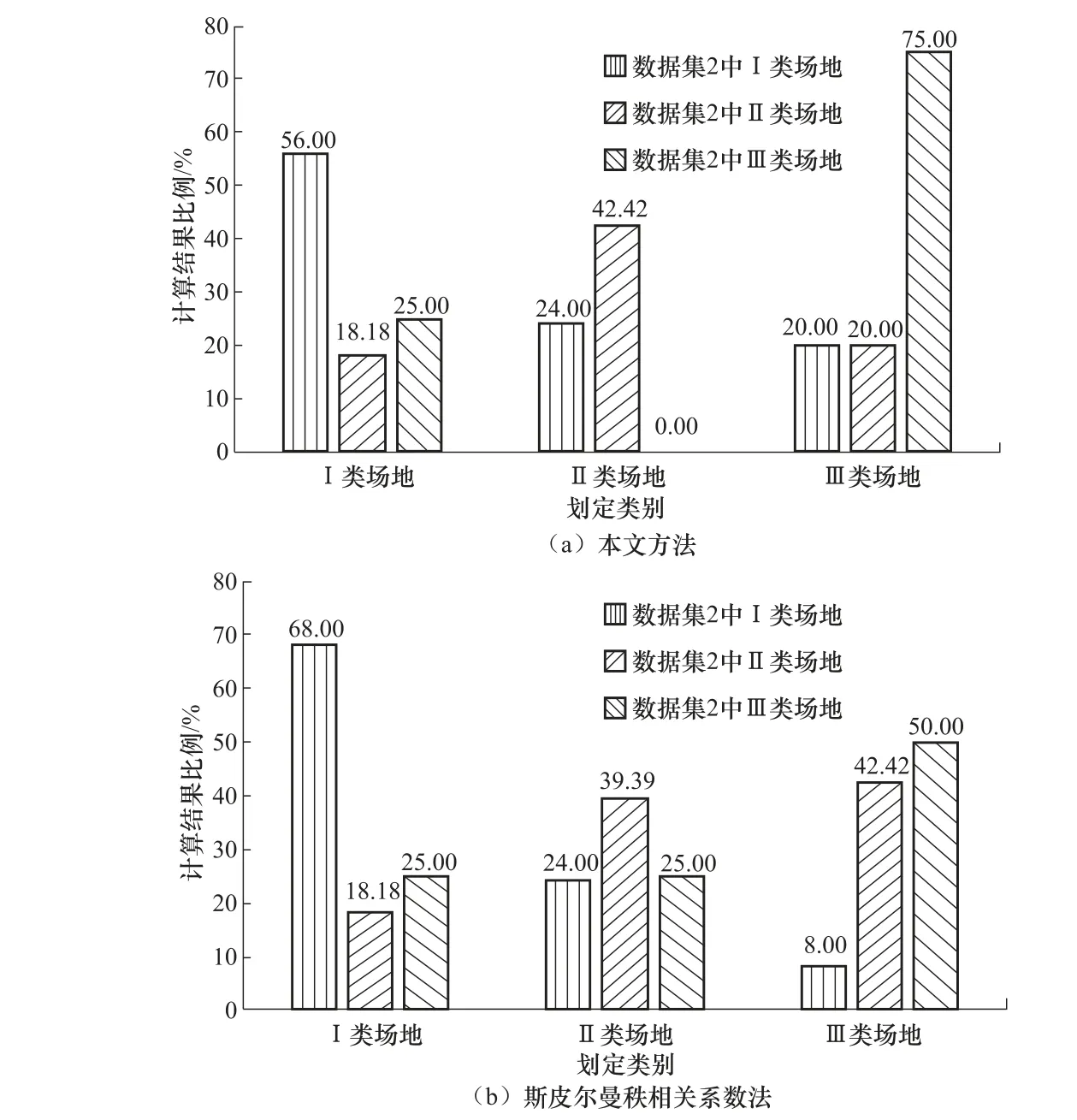
图5 2 种方法划分成功率及误判率 Fig.5 Success rates and failure rates of two classification methods

3.3 分类后谱比曲线

为从侧面验证本文方法的合理性，给出划分场地类别后的3 条平均曲线，并给出相应的自然对数标准差曲线，与由数据集1 得到的3 条标准谱比曲线对比，结果如图6 所示。

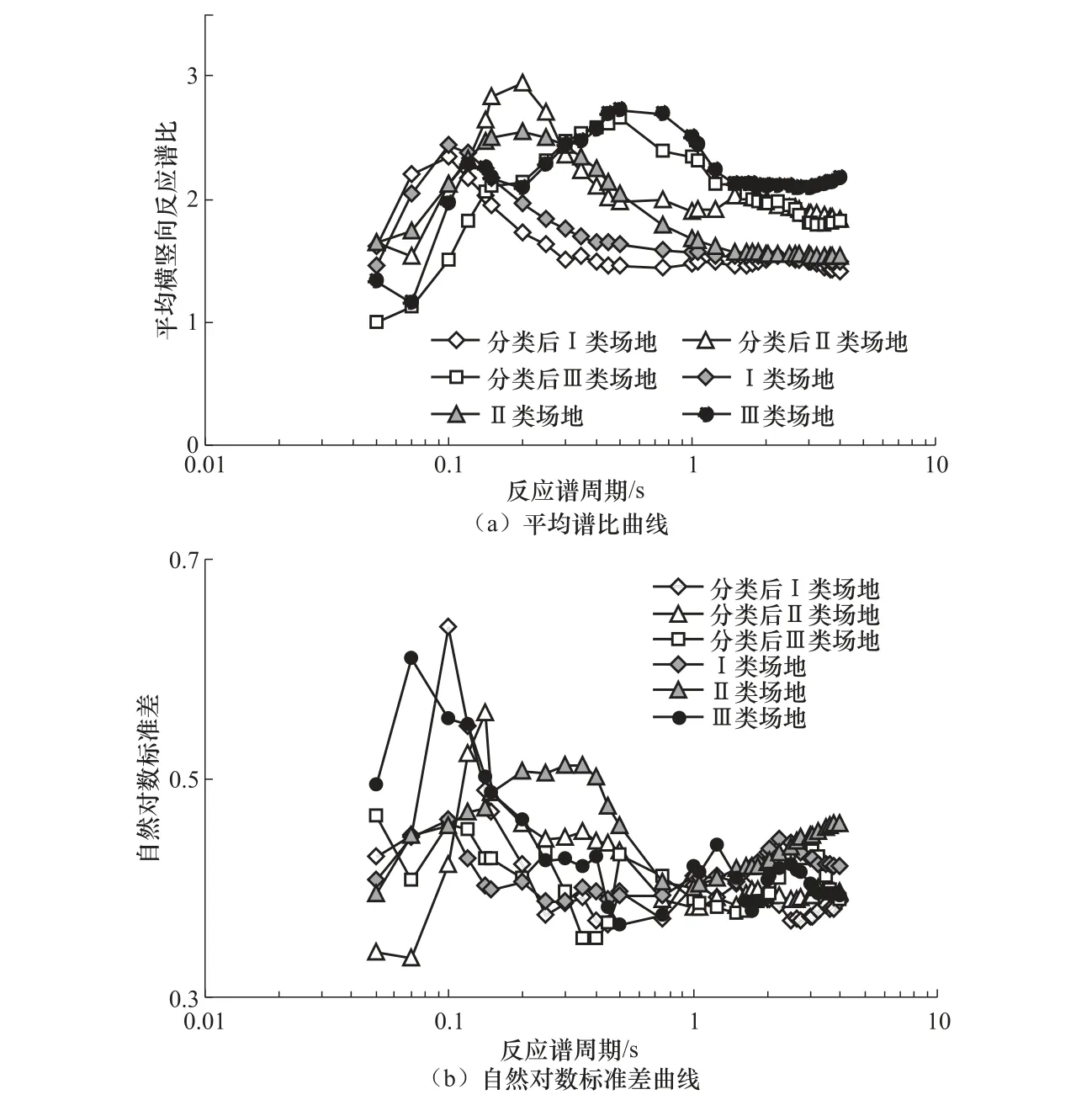
图6 分类前后3 类场地平均谱比曲线及其自然对数标准差曲线 Fig.6 Standard spectra ratio curves and natural logarithmic standard deviation before and after classification for three site classes

为从侧面验证本文方法的合理性，给出对数据集2 划分场地类别后的3 条平均谱比曲线及相应的自然对数标准差曲线，并与由数据集1 得到的3 条标准谱比曲线对比，结果如图6所示。

由图6（a）可知，经本文方法分类后的I 类场地平均谱比曲线峰值和峰值周期与标准谱比曲线基本接近，0.1s 后I 类场地标准谱比曲线的值略大，但二者下降趋势基本一致。由图6（b）可知，分类后的I 类场地自然对数标准差在0.1s 即峰值周期附近和3s 后较大，在其他周期段与标准谱比曲线较为接近。由图6（a）可知，分类后的II 类场地平均谱比曲线在峰值区（0.1s）前与II 类场地标准谱比曲线基本接近，在峰值区附近及其后的下降段则大于II 类场地标准谱比曲线，但总体形状相似。分类后的II 类场地自然对数标准差在峰值区附近大于II类场地标准谱比曲线，而其在他周期段上则比II 类场地标准谱比曲线小，如图6（b）所示。对于III 类场地，由图6（a）可知，分类后的场地平均谱比曲线仅在某些周期段上较大，而其他周期段则与场地标准谱比曲线基本一致；由图6（b）可知，0.3s 前，分类后的场地自然对数标准差较大，其他周期则二者接近。

由图6 可知，使用本文方法分类后，各类场地平均反应谱比曲线与按照钻孔信息进行场地分类得到的标准谱比曲线基本吻合。数据集2 重新分类后的平均谱比曲线及其自然对数标准差较数据集1 所得结果略有提高，但总体趋势一致，从侧面说明本文所提分类方法的合理性。

4 结论

本文利用收集到的664 个日本KiK-net 台站场地信息，按照《建筑抗震设计规范（GB 50011—2010）》进行场地分类，以此为基础构建2 个数据集，进而基于离散Fréchet 距离对数据集2 的场地进行分类，并对分类结果进行校验，得出以下结论：

（1）按照我国建筑抗震设计规范对KiK-net 台站进行场地分类，并以此为基础得到的3类场地标准反应谱比曲线在I、II、III 类场地间具有明显的区分度。

（2）使用本文所提基于离散Fréchet 距离的方法对强震台站场地进行分类，分类成功率与误判率表明该方法具有较高的准确性和可行性。

（3）将本文方法与斯皮尔曼秩相关系数法得到的强震台站场地分类结果进行比较，结合本文方法得到的平均谱比曲线，表明本文分类方法具有一定合理性。