基于地理路由和参与者协作模型的WSAN的通信机制

赵海军，贺春林，蒲斌，崔梦天

（1. 西华师范大学计算机学院，四川 南充 637009；2. 西南民族大学计算机科学与技术学院，四川 成都 610041）

1 引言

无线传感器和参与者网络（WSAN, wireless sensor and actor network）[1]是一种分布式异构设备无线通信系统，异构设备主要是传感器和参与者，其网络物理结构如图1所示。这里的参与者不同于传统的执行器的概念，它除了能够通过几个执行器在环境中工作外，还是一个执行与网络相关功能的单一网络实体，即接收、发送和转发数据。在大多数应用中，参与者是资源丰富的超大处理能力和高传输功率设备及长寿命的电池。

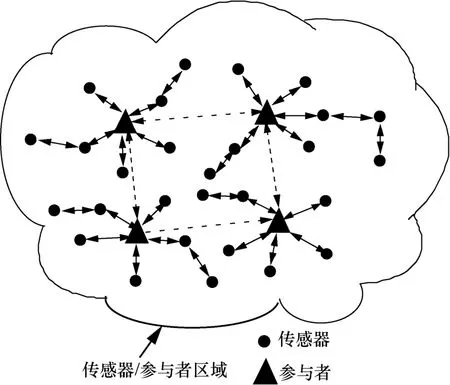
图1 无线传感器和参与者网络的网络物理结构

WSAN中的不少应用与加强和补充现有的传感器网络应用有关。在这些应用中，执行活动主要是通过启用或扩展其监控能力来增强传感器网络的操作。例如，移动参与者可以准确地部署传感器，实现对环境的自适应采样，从近距离的传感器拾取数据、缓冲数据，并将数据发送到有线接入点，或者执行能量收集[2-4]。

关于WSAN的研究，文献[5]针对静态WSAN的通信和协作问题提出了一种框架，并提出了传感器-参与者协作和参与者-参与者协作的概念，以及集中式最佳解决方案和分布启发式解决方案。文献[6]提出了一种适用于无线传感器网络的单纯事务管理模型，主要包括事务并发控制策略和事务原子提交协议。在事务并发控制方面，结合无线传感器网络的特点使用了轻量级的向前验证的乐观并发控制；在事务原子提交协议方面，提出了基于缓存和定时器的二阶段提交协议，为参与者提供了缓存机制，有效利用协调者的广播信息，降低能量消耗。在协调者和参与者中加入了定时器，定时器触发后会提供事务处理统一的结果（提交或撤销）；此外，还为协调者加入了心跳算法来提高协议的可靠性；但该模型最大的不足是未考虑协调者和参与者之间的通信机制问题。文献[7-8]研究了传感器网络中的实时通信问题，但并未就传感器和参与者之间的数据交换和协作进行研究。文献[9]针对传感器网络中数据发送的能量消耗和时延之间的权衡进行了研究。文献[10-11]采用地理位置信息对传感器网络的可扩展路由进行了研究，以减少传感器之间协作所需要的信号强度和能耗。

本文针对有移动参与者的 WSAN中的协作和通信问题进行研究，提出的主动位置管理方案以最小能量消耗来管理参与者的移动性。参与者广播其位置的更新，基于Voronoi图限制其范围，而传感器基于先前接收到的更新卡尔曼滤波来预测参与者的移动；然后得到一种基于地理路由的最佳能量感知转发规则作为传感器-参与者之间的通信，并采用功率控制来控制数据传输过程的时延，通过迫使多个参与者成为在事件区域中生成流量的接收者来解决网络拥塞；最后基于事件特征提出了参与者-参与者之间的协作模型来对参与者之间的移动进行协调，以最佳地完成任务。仿真结果表明，本文提出的关于WSAN的通信机制是有效的。

2 传感器和参与者的位置管理

假设网络由NS个传感器和NA个参与者构成，且NS＞＞NA。每个传感器配备一个低数据速率的无线接口，每个参与者配备2个无线发射器，一个低数据速率发射器用于与传感器进行通信，一个高速率无线接口用于参与者-参与者之间的通信。

根据传感器网络路由算法[5,12-13]，本文基于地理路由范式来实现传感器-参与者之间的协作管理，因为这样可以在不增加信令开销的情况下对网络规模进行扩展，且路由判决本质上是局部化的。但在具有移动节点和多个接收者的网络中，还依赖于有效的位置管理策略，才能够提供任何时刻与移动节点位置相关的节点。为此，本文提出了一种主动位置管理方法，该方法基于移动参与者发送给传感器的更新消息。在 WSAN中，每个参与者是一个等效的信息接收者，因而传感器-参与者之间的通信是局部的，即每个传感器发送信息给它的最近参与者。因此，在空域中，广播可以基于 Voronoi图[14]进行限制；同时，参与者的移动在某种程度上是可预测的，因为它是由参与者-参与者之间的协作过程驱动的。因而在时域中，位置更新可以被限制到参与者的位置，这个位置不能在传感器一侧被预测。当参与者的实际位置“远”于根据过去测量值在传感器上可预测的位置时，位置更新将在参与者上被触发。

2.1 限制广播空间

本文采用Voronoi图来限制由参与者发起的位置更新范围。一组离散站点的Voronoi图将平面分割成一组凸多边形，使多边形内的全部点都仅离一个站点最近。如果一个传感器s的位置位于一个参与者a的Voronoi图单元中，就说传感器s由参与者a控制。每个参与者负责其Voronoi图单元中传感器的位置更新，并调节其功率，以限制超出其Voronoi图单元的最远点的干扰，因此每个传感器希望从控制它的参与者处接收位置更新。如果参与者能够在一跳中到达其Voronoi图单元中的全部传感器（这在许多实际情况下是可能的），则大部分的能量消耗在参与者上。

2.2 限制广播时间

在二维坐标系中，第i个参与者的动态运动模型可以采用状态空间法[15]得到其等价的离散时间动态方程，即

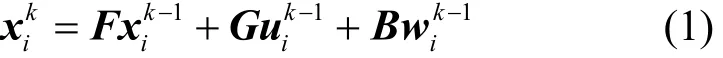
式(1)表示系统的状态转移方程，描述了第i个参与者在时间步k-1和k之间的运动，其中，有

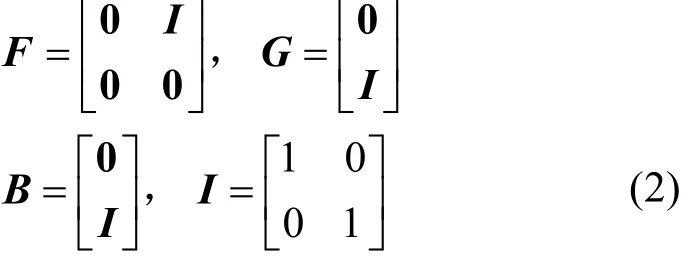
时间步k与第i个参与者观察到的位置和状态有关，可用测量方程表示为

卡尔曼滤波[16]提供了一组高效计算的递归方程来估计参与者的动态运动过程的状态，本文利用它来估计参与者的位置，并在传感器上预测参与者的位置，从而减少信息交换。参与者的位置可以基于在参与者上得到的测量值zik并在参与者的Voronoi图单元中的传感器上进行估计和预测，通过参与者广播。在时间步k，第i个参与者的Voronoi图单元中的每个传感器s根据式(4)更新状态（参与者的位置和速度）。

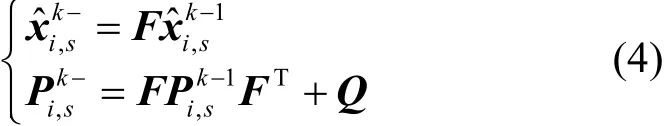
式(4)描述了在接收测量值之前（先验估计值）传感器s如何预测参与者的状态。注意，控制输入在传感器上是未知的，同时被用于参与者更新状态；然后，传感器s预先预测协方差矩阵，在接收到来自参与者的测量值后，更新卡尔曼增益（如式(5)所示），并根据测量值校正状态估计值（如式(6)所示）和协方差矩阵（如式(7)所示），即

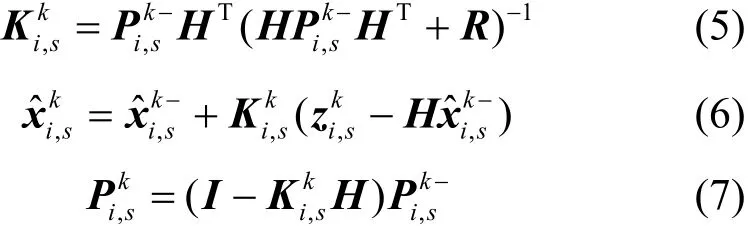
在每个时间步k，每个参与者都试图在它的Voronoi图单元中的传感器上执行预测过程，通过对新的测量值滤波，计算其实际新的位置，并广播新的测量值如果传感器s在时间步k没接收到位置更新，则假设即预测的位置与参与者实际的新的位置一致，在此基础上，按式(5)～式(7)更新参与者的状态估计值。

3 传感器-参与者之间的通信

本文提出了一种可靠性概念，即由一个参与者感知到的事件可靠性r是在一个判决间隔中的可靠数据分组与接收到的全部数据分组的比值，如果在给定的时延范围内数据分组被接收，则认为这个数据分组是可靠的；事件可靠性阈值rth是所要求的最小的事件可靠性。本文的目标是当数据必须在一个给定的时间限制内以一个给定的可靠性阈值rth交付时，换取的能量消耗时延。

3.1 基于功率控制的能量时延调节

大多关于地理路由的研究主要考虑贪婪转发，即将数据分组转发给最接近目的端的节点，然而，这通常需要选择将转发节点连接到位于传输范围边界附近的邻居。当考虑一个实际的物理层时，这种连接很可能是不稳定的，容易产生高分组差错率，故本文提出在节能链路上转发数据分组，使在每个单跳上的能量消耗达到最小化。本文不考虑大多数路由研究所采用的单位圆盘图假设，而是考虑一个更精确的连通模型，即首先得到在快速衰落信道下的节能转发距离，然后提出一种通过增加发射功率来减少端到端时延的机制。

考虑转发器vi和vj之间的通信，用dij表示2个转发器之间的距离，则vj接收由vi发送的数据分组的概率可以表示为

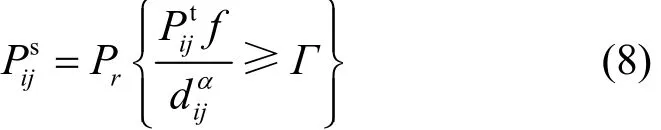
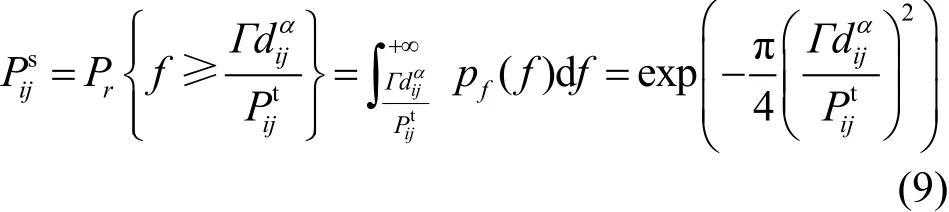
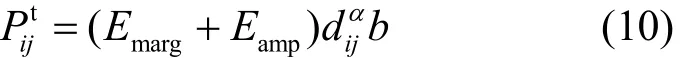
其中，Eamp是一个常数，单位为J/(bit⋅m)，Emarg是包含允许期望分组差错率项的调整项，单位为J/(bit⋅m)，表示在有α损耗下每米每比特所需要的能量。较高的Emarg值会导致较高的能量消耗，同时增加接收器成功接收的概率，减少预期的重发次数。

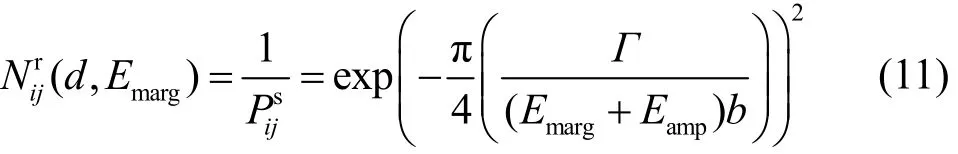
考虑节点vi向其距离为D的目标参与者ak转发一个数据分组，且链路指标E=2Eelec+Eampdα，其中Eelec是收发器电路发送或接收1 bit所需的能量，单位为J/bit，则端到端能量消耗可以表示为

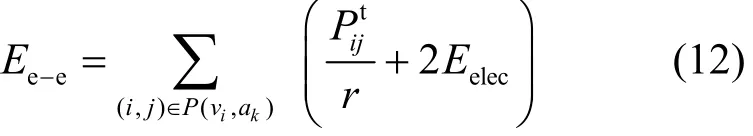
其中，P(vi,ak)表示vi和ak之间的路径。理想情况下，当数据在一组位于连接源和目的线路节点上（节点间距离等距dopt）转发时，端到端能量消耗就达到最小化。通过将式(10)代入式(12)，并考虑重发可得到

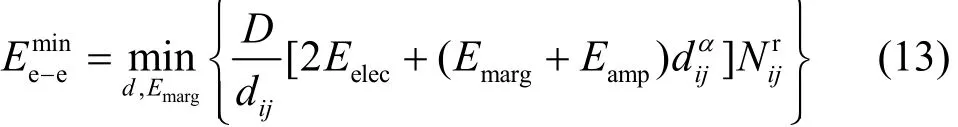
一个稳定点的充分条件是一个极小值，该极小值通过Hessian ∇2Ee-e在稳定点计算得到。最佳转发距离dopt与D无关，D为转发节点和目的端之间的距离。式(13)可以解释为距离无关和距离有关的能量消耗之间的最佳折中，并且适合于局部转发规则。在理想信道情形且Emarg=0时，当时，式(13)就达到最小化。

当Eelec=50 nJ/bit，Eamp=100 pJ/(bit.m)，α=2.5时，对于理想信道来说，最佳转发距离dopt=13.47 m。求解式(13)得到一个瑞利衰落信道上的dopt=8.00 m且Eoptmarg=86 pJ/(bit.m)，即Eoptmarg≈Eamp。因此，当在一个瑞利衰落信道上的期望最佳转发距离比理想信道情况低时，所需的发射功率就更高。

于是得到结论：能量最优路径是通过将数据分组转发给位于dopt（单位为 m）之外连接转发节点和目的节点的线路上来得到的，称这个二维平面上的点为最佳转发点。一个实用的转发规则应该选择与这一点有最小距离的下一跳。当下一跳比最佳转发点更接近目的节点时，期望的能量消耗会明显增加。因此，在这种情况下，把下一跳选择为离最佳转发点最近的节点，即那些不比最佳转发点更靠近目的节点的节点。

可靠性可通过参与者反馈信息来控制。当事件发生时，全部传感器都以最大转发范围开始传输。然后，根据观察到的参与者反馈的可靠性，传感器可以减小它们的转发范围，直至可靠性接近所要求的事件可靠性阈值rth，或达到最佳转发范围。当在最大转发范围内观察到的可靠性较低时，参与者就启动网络层拥塞控制程序。

3.2 基于参与者驱动的拥塞控制

每当参与者ai检测到由过度时延和数据分组丢失造成非常低的可靠性时，则选择另一个参与者重新发送来自其Voronoi图单元中的一半传感器的流量给这个参与者。每个参与者ak被ai分配一个权值wk，这个权值用于度量它成为一个在部分事件区域得到的流量接收者的合理性。权值

1) 拥塞因子ηk(0≤ηk≤1)。这个值反映了在参与者ak上观察到的可靠性，即如果r＜rth-ε，则ηk=1，当r-rth增大时，ηk单调减小；对于那些没接收流量的参与者来说，ηk=0。其中ε表示可靠性的适当裕量，以避免不稳定。

2) 指向性因子δk。这个值反映了参与者ak相对于参与者ai和事件区域中心的相对角位置。

图2说明了参与者ai正从事件区域的一部分接收数据的情况。图2中，Cev为事件区域的中心，表示传感器位置的加权和，位于ai的Voronoi图单元中的事件区域的部分中心为Cev,i。在图 2给出的事例中，事件区域被分成两部分，且另一个参与者从事件区域的第二部分接收数据。在一般情况下，事件区域在多个参与者间被划分，假设全局事件的中心Cev已由参与的参与者合作重建，这样，将给予位于关于Cev,i的ai的同方向的参与者更高的权值，因为这将导致在ai方向的流量增加，或在关于Cev,i的Cev方向的流量增加，从而增加事件区域的流量；相反，对于远离这2个方向（图2中的最佳方向）的那些参与者的指向性因子应该是最大的。角度α、β和θk分别描述了Cev,i与ai、Cev和ak的相对角位置。

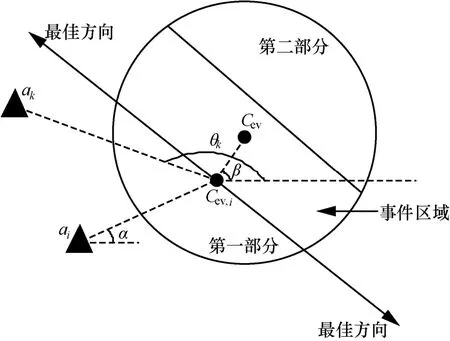
图2 指向性因子δi的计算

参与者ak的指向性因子的计算式为

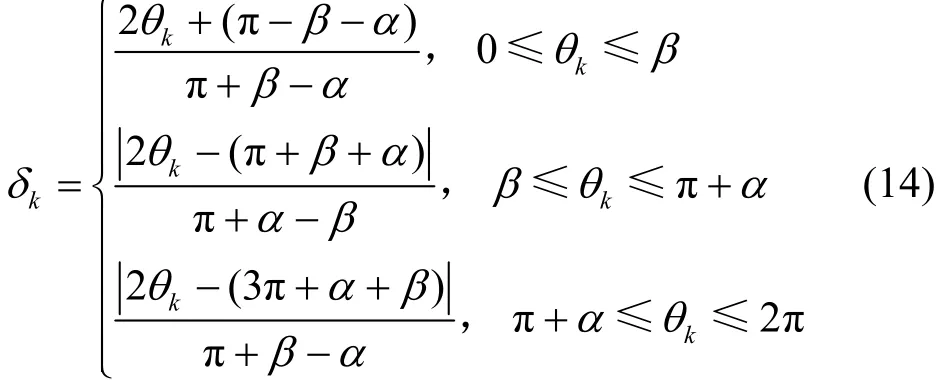
一个拥塞的参与者ai选择具有最小权值wk∗的最佳参与者ak∗。然后，参与者ai计算并告知ak∗的一个新的虚拟位置给其 Voronoi图单元中的传感器。虚拟位置必须位于连接参与者的实际位置xk∗和事件区域Cev,i的线路上，而且对应于Cev,i中的一半传感器更接近于ai的点，而另一半传感器更接近于ak∗。每个传感器将选择其接收参与者，对于参与者ak∗，采用虚拟位置而实际位置xk∗仍用于执

3) 距离因子Δk。它是参与者距离事件中心Cev,i的距离，归一化为监控区域的直径，即当距离最大时，Δk=1。行实际的转发功能。虚拟位置允许以这种方式最佳地划分传感器，只有那些更接近ak∗的传感器重新发送它们的流量给ak∗，并通知传感器。这个过程由在流量分割后仍然拥挤的参与者递归运用。

4 参与者-参与者之间的协作通信

本节构建多个参与者任务分配问题，其目标是协调它们的移动性。一般而言，选择最好的参与者构成参与者团队，并控制它们向作用区域移动。

通过上述分析可知，生成读数的传感器的位置定义了事件区域。作用区域表示参与者应当起作用的区域，并通过处理事件数据来识别。通常情况下，事件区域和作用区域可能是不同的。

根据从作用区域收集到的事件的特征，在事件空间Ω中发生的每个事件ω可以用数组Ψ(ω)={F(ω),Pr(ω),A(ω),S(ω),I(ω),D(ω)}来描述，其中，F(ω)描述事件的类型，即事件所属的类别；Pr(ω)描述的是优先级；A(ω)描述的是事件区域，单位为 m2；S(ω)描述的是作用区域，单位为m2；I(ω)描述的是强度，单位为 J/m2；D(ω)描述的是作用完成的时间限制，即从事件被感知到完成相关作用的最大允许时间，单位为 s。这些确定每个发生事件的特征参数由接收传感器信息的参与者分布式重构，并构成多个参与者任务分配问题的输入；多个参与者分配问题包括选择一个参与者团队和它们的速度，以最佳地划分作用工作量，使完成作用所需的能量最小化，同时满足作用完成的约束时间。尽管参与者是资源丰富的节点，但作用和移动所需能量的数量级要高于通信所需的数量级，因此，重要的是要节省作用和移动的能量，以延长参与者的寿命周期。本文把多个参与者的分配问题构建为一个混合整数非线性规划（MINLP, mixed integer non-linear program）。

首先假设：1)执行作用的能量（作用和移动能量）比通信所需要的能量要高；2)由于缺乏资源，只有当与更高优先级的事件相关的作用无法完成时，才执行任务再分配。

ηfa：参与者a在一个事件类型f∈F(ω)上执行的效率，即用于作用区域的作用能量所产生的效应与作用能量本身之比。参与者a在事件ω发生时得到的可用能量，单位为J。

TC：协作时延，即处理事件数据、重建事件本身，并通过求解问题来选择参与者团队所需要的时间，不依赖于事件，单位为s。当事件ω发生时参与者的子集，即没有分配给在与先前发生事件相关联的作用区域执行的参与者。发送数据分组给参与者a的资源总数，而是一个惩罚函数，单位为J，它对参与者a的选择进行加权，参与者a接收来自源的数据，是一个执行团队的一部分。惩罚函数随的增加而单调增加。

寻找

最小化

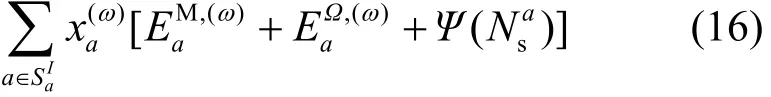
满足条件

约束式(17)确定了参与者a移动到由发生事件确定的作用区域所需要的能量，是移动所需的功率和以给定速度到达作用区域所需的时间的乘积；时间为参与者离作用区域的距离与所选择的速度的比值，即式(18)；约束式(19)限制了每个参与者的速度范围；当参与者a是一个参与者团队的一部分时，约束式(20)确定了a完成作用所需要的能量；约束式(21)确保所选择的团队能够完成分配的任务，给定组成团队的参与者的特点和事件的范围及强度；约束式(22)限制执行完成时间和需要移动参与者团队所需要的时间总和要小于作用完成时间与协作时延之差；约束式(23)确保每个参与者有非负的剩余能量；约束式(24)保证至少有一个参与者作用于告知的作用区域。

5 方案性能评价及分析

5.1 传感器-参与者之间的通信

仿真平台采用J-Sim[17]，J-Sim采用新的进程驱动机制，且兼容离散事件的驱动。J-Sim采用分裂对象模型：可用Java语言编写网络组件，采用TCL脚本来描述仿真场景、拓扑结构及链路中使用的算法和协议，并对这些对象进行配置和组合；通过 J-Sim可以很容易建立网络拓扑、节点结构和通信行为，从而实现网络仿真，达到评价网络算法和协议的目的。

对于传感器-参与者之间的通信，传感器执行3.1节中所描述的地理转发算法，MAC层基于CSMA/CA，物理层执行本文提出的功率控制过程并设定带宽和功耗参数，类似于IEEE 802.15.4兼容无线电。监控区域是一个200 m×200 m的正方形区域，随机部署200个传感器。传感器的最大传输范围设置为40 m，带宽设置为250 kbit/s。传感器发送56 B的数据分组，采用每秒一个数据分组的报告率，队列大小设置为20个数据分组，仿真执行持续400 s。

图3和图4分别为中、低流量情形下（即事件分别围绕中心40 m和20 m的范围）仿真运行得到的平均功率消耗和端到端时延与转发范围的关系。事件区域为圆形，且中心在（100 m, 100 m），在事件区域内的传感器报告测量值给参与者。在中流量情形下，需要对位于事件区域内的7个传感器求平均；在低流量情形下，大约有25个传感器。由图3和图4可知，低流量情形下的平均功率消耗和端到端时延都低于中流量情形，而且在中、低流量情形下，端到端时延一开始随着转发范围的增大而持续降低，这是以增加功率消耗来换取的，而后趋于稳定。

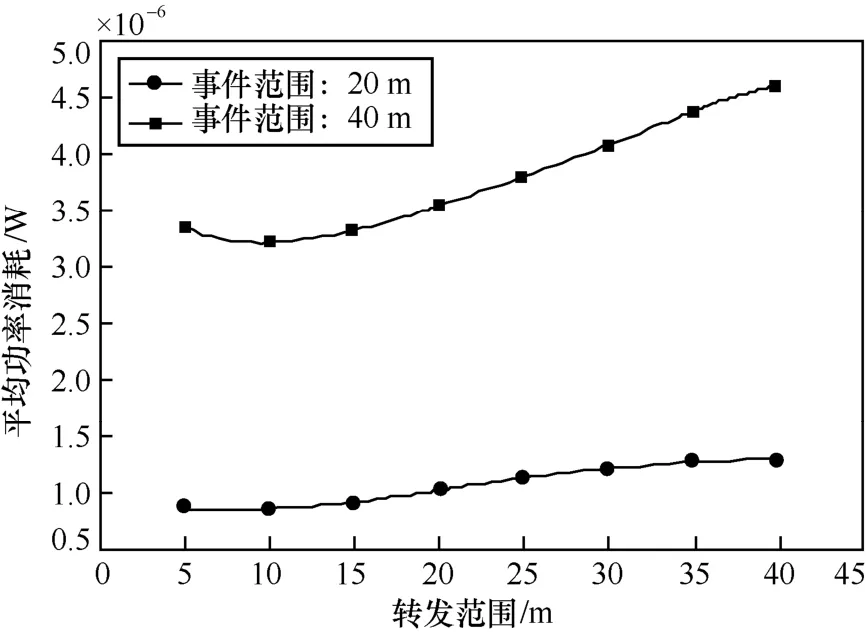
图3 中、低流量情形下平均功率消耗与转发范围的关系

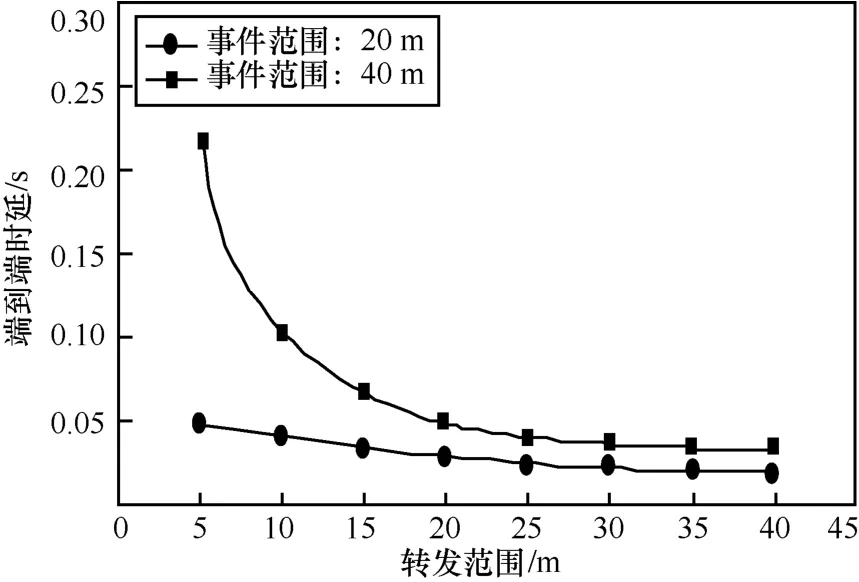
图4 中、低流量情形下端到端时延与转发范围的关系

图5～图7为高流量情形即事件范围设置为60 m（相当于平均57个传感器）且事件区域完全位于一个单一的参与者 Voronoi图单元里得到的仿真结果。仿真结果比较了一个参与者（对应于不采用3.2节所设计的拥塞控制程序）和2个参与者（对应于采用 3.2节所设计的拥塞控制程序）接收事件区域生成流量时的平均功率消耗、端到端时延和分组丢失率。

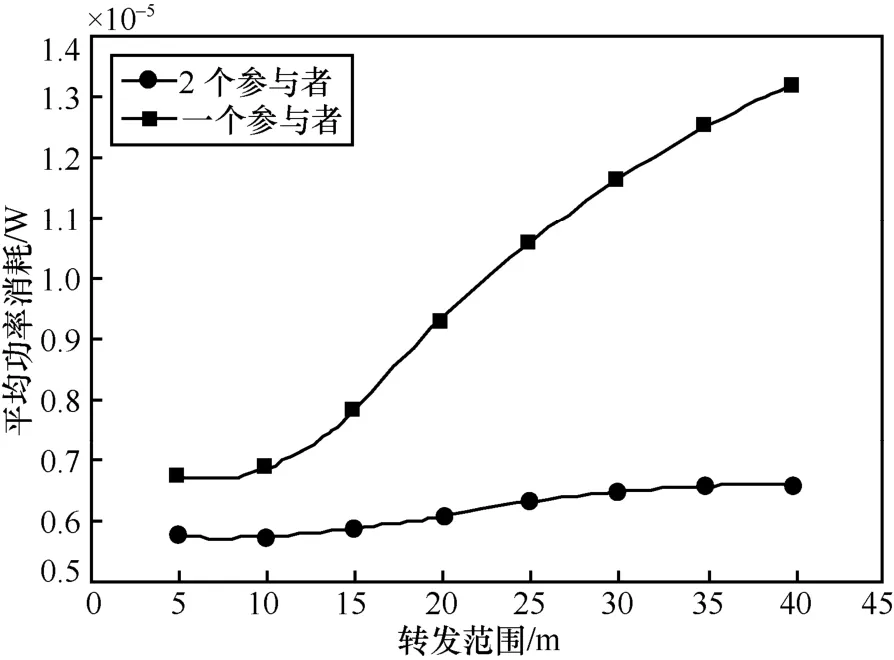
图5 高流量情形下平均功耗与转发范围的关系

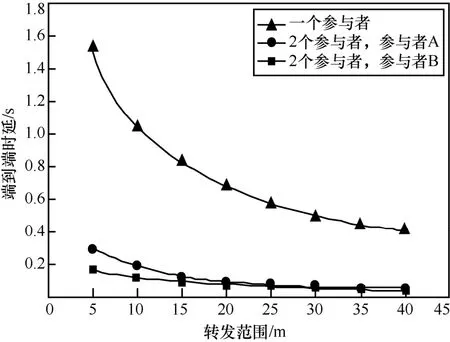
图6 高流量情形下端到端时延与转发范围的关系

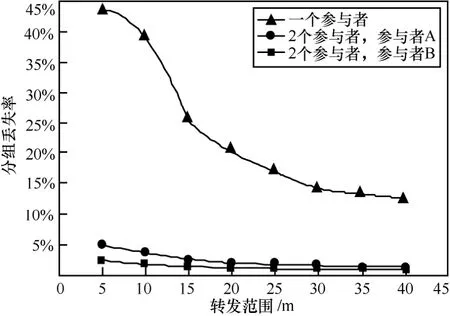
图7 高流量情形下分组丢失率与转发范围的关系

从图5～图7可以看到，在不采用本文提出的拥塞控制程序时，由于事件区域本身是拥挤的，因此数据分组被丢弃的比例较高，如图7所示，大约为14%～43%。同时端到端时延平均增加了约1 s，且不易通过改变转发范围来控制，如图6所示。相反，当采用本文提出的拥塞控制程序时，将事件数据在2个参与者之间进行划分，拥塞可以大大降低，这是由于大多数拥塞和分组丢失发生事件区域的多个节点尝试同时发送，当在事件区域的另一侧的第二个参与者接收数据时，拥塞就得到了显著的改善，因为流量从事件区域被转移了，所以分组丢失率接近于0，如图7所示，平均时延也降低了近2个数量级，且可以采用功率控制来调节，如图 6所示。重要的是，即使第二个参与者远离事件区域，数据分组过早地在它们的源参与者路径上被丢弃，功耗也会通过拥塞控制程序被降低，主要是由于在MAC层上减少了数据分组的重传，如图5所示。

5.2 参与者-参与者之间的协作通信

假设参与者随机部署在200 m×200 m的区域，事件强度I=0.5 J/m2，作用范围S=42π m2随机出现在整个区域，设置作用完成时间限制D(ω)和协作时延TC分别为14 s和1 s。考虑同类参与者的情形，其β=0.05 W/(m.s-1)，γ=1.5，效率η=1，作用功率l=1 W/m2，初始能量E0=1 000 J，速度为3～12 m/s。

图8和图9分别为能量消耗和时延与最大团队规模之间的关系，图10为能量消耗与构成一个团队的参与者的数目固定且等于团队大小的关系。可以看出，当参与一个执行团队的参与者数目最优以使总的能量消耗（即移动能量EM和执行能量EΩ的总和）最小时，则至少需要3个参与者来完成执行，如图8所示。且总的执行时间正好是作用完成时间限制D(ω)减去协作时延TC，即13 s，如图9所示。问题趋于使参与的参与者数目最小化，并将更高的速度分配给那些更接近作用邻区域的参与者。这可以通过考虑每次一个参与者需要移动所消耗的一个固定大小的功率来解释，无论其速度如何。相反，当全部参与者必须成为团队的一部分时，执行时间是以牺牲能量消耗为代价来减少的，如图10所示。

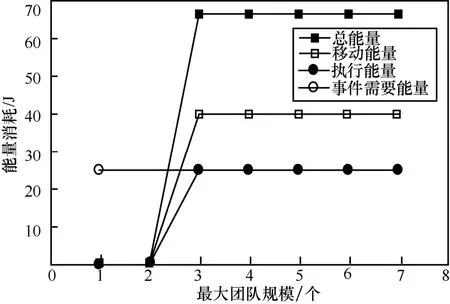
图8 能量消耗与最大团队规模的关系

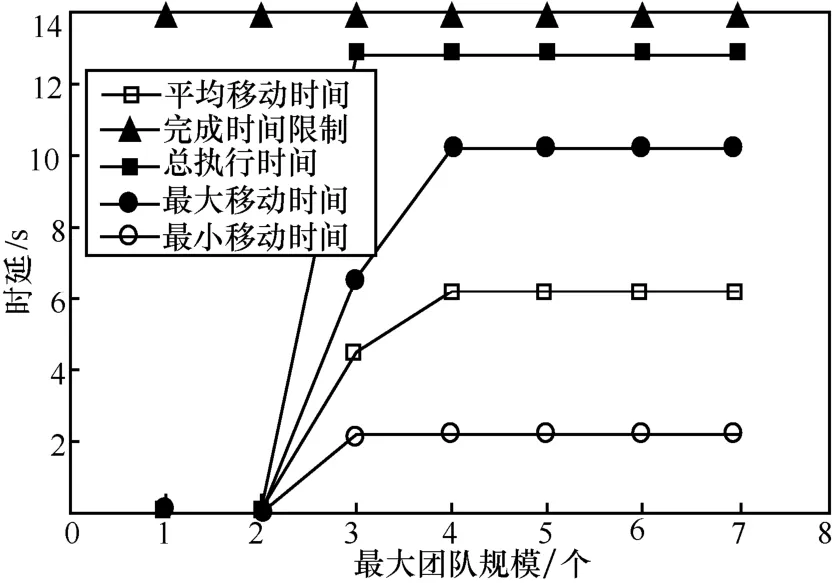
图9 时延与最大团队规模的关系

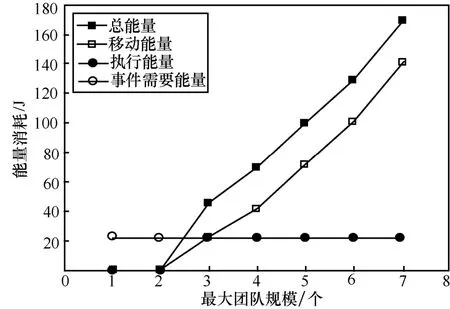
图10 能量消耗与团队规模的关系

5.3 与文献[6]提出的单纯事务管理模型的比较

本节给出采用本文提出的通信模型与文献[6]提出的单纯事务管理模型在中等流量情形下（大约25个传感器）的比较结果。图11为2种模型在平均时延、节点能量消耗和分组丢失率方面的仿真结果。

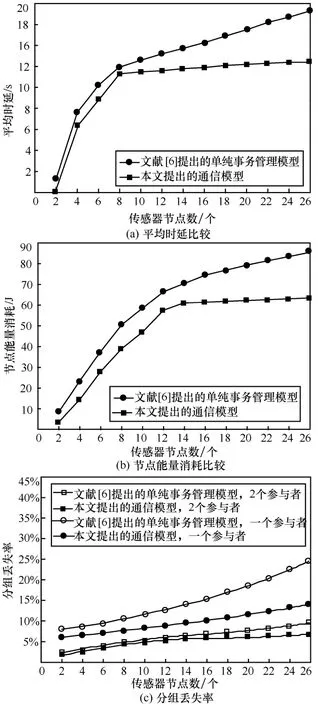
图11 本文提出的通信模型和文献[6]提出的单纯事务管理模型的比较

从图 11(a)和图 11(b)可以看出，由于本文提出的通信模型既考虑了节点间的数据路由和交换问题，同时也考虑了节点和参与者之间及参与者和参与者之间的通信机制，因此在平均时延和节点能量消耗方面均优于文献[6]的单纯事务管理模型，而且当达到一定节点数时，随着节点数的增加（对应流量增加），本文提出的通信模型在平均时延和节点能量消耗方面增加并不明显，说明本文提出的通信模型是顽健的和可扩展的。

图11(c)为2种模型在高流量和事件范围20 m及一个参与者和2个参与者情形下得到的分组丢失率仿真结果。由图11可知，尽管2种模型的分组丢失率随着传感器节点数的增多而增大，但本文提出的通信模型无论在一个参与者还是2个参与者时都要低于文献[6]提出的单纯事务管理模型。特别是在一个参与者时，由于文献[6]提出的单纯事务管理模型使用了节点缓存机制，随着传感器节点数的增加，需要维持各个节点的提交矩阵，导致动态内存消耗增加而出现缓冲溢出，从而增大分组丢失率；而在2个参与者时，当传感器节点数较少时，文献[6]提出的单纯事务管理模型尽管使用了节点缓存机制，但2个参与者有足够的缓存接纳各个节点的提交矩阵，所以其分组丢失率非常接近本文提出的通信模型的分组丢失率，但仍高于本文提出的通信模型的分组丢失率。

6 结束语

本文研究了具有移动参与者的无线传感器和参与者网络中的通信问题，并针对传感器-参与者之间和参与者-参与者之间的协作通信问题提出了有效的解决方案。首先，采用传感器最小能量消耗，提出了一个主动位置管理方案来处理参与者的移动性；然后，基于地理路由，提出了一种传感器-参与者之间通信的有效节能解决方案，并给出了如何基于功率控制来控制数据传输过程的时延，以及如何通过迫使多个参与者共享事件区域产生的流量来处理网络拥塞；最后，基于事件的特征，提出了一种参与者-参与者之间的协作通信模型来协调它们之间的运动。结果表明，本文提出的关于 WSAN的通信机制在减少端到端时延、能量消耗和分组丢失率方面是有效的。未来将针对选择最佳参与者来形成参与者团队，以执行特定要求的作用，并驱动参与者向相关的区域移动进行深入研究。