钢轨踏面的空气耦合超声检测方法∗
常俊杰 李媛媛 胡 宸 邬瑞峰 卢 超
(1 南昌航空大学 无损检测技术教育部重点实验室 南昌 330063)
(2 日本探头株式会社 横滨 2320033)
(3 中车唐山机车车辆有限公司 唐山 063035)
0 引言
发展迅速的高速铁路是我国国力强大的一大表现。但在列车的前行和制动过程中,运行列车车轮对钢轨轨头长时间产生挤压、摩擦、弯曲和冲击,车轮与钢轨的接触是点面积接触,由于车身的质量很高,加载在踏面的小面积上,在接触面产生接触应力。这种交变载荷产生疲劳应力,使局部产生塑性变形,同时致使局部的晶格产生错位,这些错位的晶格会在晶粒的边界堆积起来,最后产生具有隐藏性和危害性的微细裂纹[1−3]。浅表面的细微裂纹肉眼难以分辨,若不进行及时检测维修则会形成向四周扩散的裂纹,严重时轨道会发生断裂,极大威胁着列车的运行安全。常用检测钢轨踏面缺陷的方法有电磁检测法、涡流检测法、敲击法等[4],但这些传统方法均存在一些缺点;常规超声检测适用于在役检测,对人体无害,但耦合剂的使用会对检测效率及效果产生影响[5−6],尤其是对浅表面裂纹的检测,耦合剂极易填充到浅表面裂纹中,造成漏检。空气耦合超声检测方法弥补了上述缺点,笔者提出了使用空气耦合超声的方法对铁轨踏面进行检测。空气耦合超声检测技术具备非接触、非破坏、非浸入及安全无害的特点,十分适合在役检测[7−9]。文中首先利用半有限元法求解了CHN60型钢轨轨头踏面部分的振动模式,抽出了钢轨轨头踏面的振动模态结构和频散曲线;其次设计了空气耦合探头并搭建实验系统,根据Snell法则和圆形声源在空气中的声场分布确定了检测参数;最后从理论和实验两方面着手对钢轨踏面浅表面裂纹的有无进行了检测,证明了空气耦合超声检测方法的可行性和可靠性。
1 检测方法及原理
超声导波在板材和管道中的研究已经进行了成功的应用,但钢轨踏面中的导波不同于无限大平面的经典表面波,国内外许多学者已经对超声导波在钢轨中的传播做了大量的实验研究及数值分析。Wilcox等[10]、Cawley等[11]应用导波方法对钢轨的腐蚀进行了检测试验,但未对检测导波的模式和激发方法做介绍。Hayashi等[12]不仅通过半解析有限元的方法计算得到导波在钢轨踏面中的理论相速度及群速度曲线,还使用空气耦合超声实验方法基于二维傅里叶变换得到与计算值基本符合的轨头踏面频散曲线。
本文使用的半解析有限元方法,是一种求解三维任意横截面弹性声波导中导波传播有效数值的方法[13]。该方法的基本原理是对三维钢轨模型截面划分成多个网格单元,如图1所示。导波在钢轨z传播方向上采用正交函数exp(iξz)来表示,其中ξ是导波的波数,而第m个特征值ξm表示第m个共振模式的波数。包括钢轨在内的棒状结构的任意截面,二维截面的纵方向(z方向)上的波由正交函数exp(iξz)描述。同理,波数可以作为特征系统的特征值ξm,进而可以描绘出频散曲线。

图1 半解析有限元法中铁轨被分成小的棱柱元素Fig.1 Semi-analytical finite element method in the rail is divided into small prismatic elements
使用上述的半解析有限元法,对我国CHN60型高铁轨道进行分析,为了获得频散曲线,横截面如图2所示,横截面上的节点数为671。这些细分网格可能不足以获得精确的解,但可以粗略估计频散曲线。导轨与板材和管材略有不同,导轨的基本模式很多[13−14]。通过对所有点的特征向量ϕRm进行计算,发现许多模式在钢轨中都是没有实际的振动。因此,使用全部波的结构的数据提取了主要的模式。这里引入主导模式值(Dominant mode value,DMV)[15]来提取主导模式。

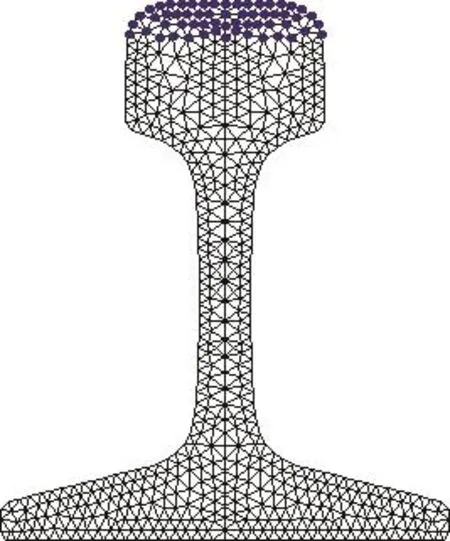
图2 用于主模式计算的细分和选定节点Fig.2 Segments and selected nodes for master mode calculation

图3 铁轨主要模态的群速度频散曲线Fig.3 Group velocity dispersion curves of the main modes of the rail
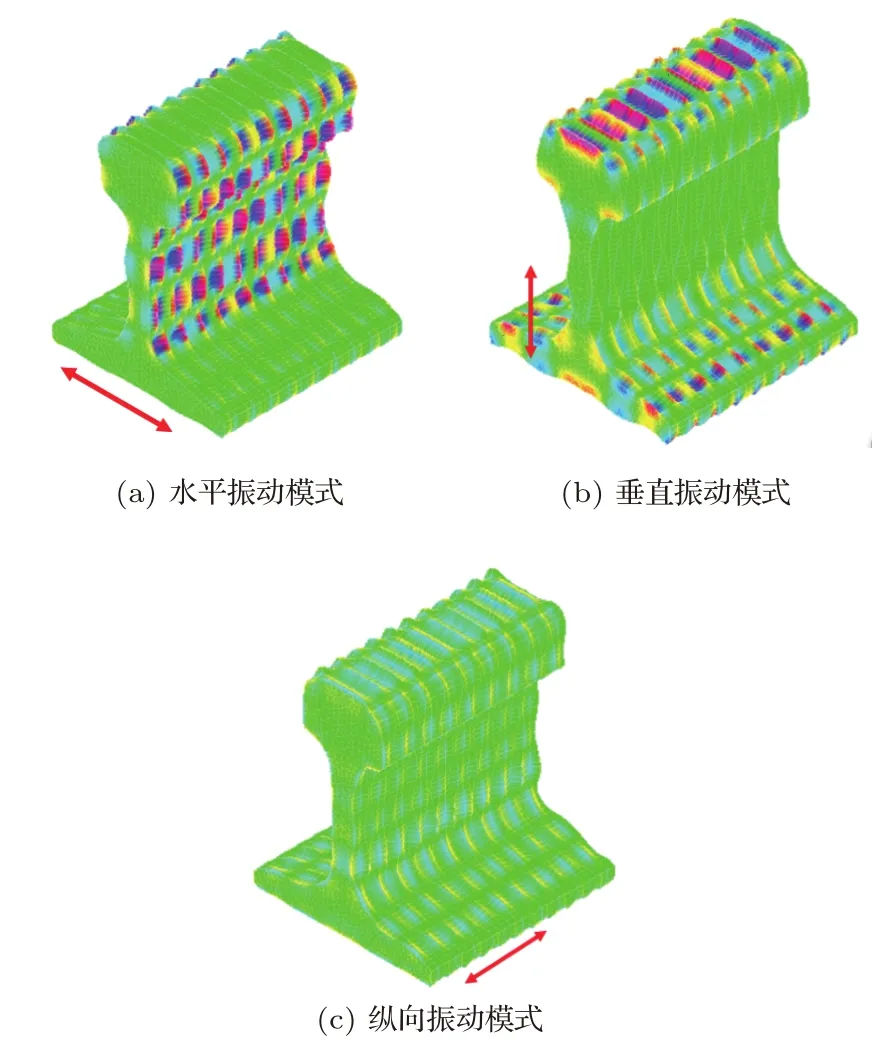
图4 与图3中的箭头所指位置相对应的振动模式Fig.4 Vibration modes corresponding to the position indicated by the arrow in Fig.3
如图2中所标注点所示,抽取钢轨踏面上部58个节点的波形结构和频散曲线,如图3、图4所示。图3(a)∼(c)分别是在选定节点处的x(水平方向)、y(垂直方向)和z(纵方向)方向振动的主模式的群速度频散曲线,颜色由灰色到黑色表示对应的DMV的值由0.2开始逐渐增大,DMV值越大,则在轨头踏面边缘有更大的振动。图3(a)∼(c)中对应的光标位置位于400 kHz时,其振动模式的波形结构如图4(a)∼(c)所示,可以看出,由于轨底截面形状不规则,轨底的三种振动模态都存在着很多种导波模式。
在此研究基础上,水平振动作为导波检测的主要模式。平坦频率区域在模式的速度频散曲线(图3(a))DMV值较小,这意味着水平振动模式在很大程度上在踏面部分的主导模式振动能量很小。
垂直振动模式(图3(b))和纵向振动模式(图3(c))平坦频率区域分布广泛。同时考虑图4中的振动模式波形结构中,水平方向(图4(a))的振动主要分布在轨道腰部,垂直方向(图4(b))的振动主要分布在踏面部分且振动较明显,纵向(图4(c))振动在整个钢轨模型中且程度不明显。可见更多的能量集中在高频率的垂直方向上,表明此模式对于钢轨踏面的导波检测十分适用。这些模态可以看作是在钢轨踏面上面传播的类瑞利波传播。瑞利波是沿半无限弹性介质自由表面传播的偏振波,但被检测的钢轨踏面并非半无限大弹性介质,因此在检测的过程中使用的是这种沿钢轨浅表面传播的类瑞利波。
当采用斜探头来激励和接收钢轨踏面垂直振动模态类瑞利波时,发射探头入射角度θ关乎类瑞利波能否出现,入射角度θ可以根据Snell定律计算得出:

其中,cair为超声波在空气中的传播速340 m/s;cp为超声类瑞利波在钢材中的相速度。由我国60型高铁铁轨轨头踏面的频谱分析,通过改变黄色光标的位置,可以得到所使用频率的超声波在钢材中的相速度cp的结果,由公式(1)得到所使用的入射角。本研究过程中,使用0.4 MHz频率探头,选取垂直振动模态下相应相速度为cp=3181 m/s,即由公式(1)可得入射角θ=6.14◦。
2 实验结果及分析
2.1 实验过程
首先利用二维超声波仿真软件WAVE2000 plus建立对向类瑞利波法检测的模型,釆用高精度的时域差分方法(Finite-difference time-domain,FDTD)求解完全的黏弹性波动方程,一次求出全程的超声波传播。如图5所示,利用如下模型来研究这种方法中信号在试件中的传播情况。
使用频率为0.4 MHz,缺陷角度固定为90◦,以缺陷深度为5 mm、宽度为0.5 mm为例,探头尺寸为 14 mm×20 mm,入射角为6.14◦,设置真空隔板以便对超声波传播过程进行研究。图6为超声波的传播过程,白色部分表示超声波能量较大。如图6(a)所示,10µs时超声波以纵波形式在空气中传播,能量较大;如图6(b)所示,在25µs时超声波开始传播到钢轨中,并以类瑞利波形式向前传播;在图6(c)中,40µs时超声波通过缺陷传播,同样以类瑞利波形式向两侧传播;在图6(d)中,60µs时由工件向外泄露的超声波信号被接收传感器接收。
实验装置由钢轨,JPR-600C信号源处理,计算机,前置放大器,晶片大小为14 mm×20 mm、频率为0.4 MHz的空气耦合探头组成了检测系统,探头摆放方式为将探头置于与缺陷等距离异侧,接收被缺陷阻挡后绕过缺陷的波作为有效信号(图7)。对实际轨道进行检测时,采用空气耦合的方式在激励轨道垂直振动的方向放置激励源的测量方法,如图8所示,利用空气耦合类瑞利波法对不同的缺陷进行了检测,实验中使用的探头为特制的高信噪比空气耦合超声波探头,并使用带订制角度卡槽的塑料板对空气耦合探头进行固定。
空气耦合探头的底端距钢轨表面3mm,发射探头和接收探头的中心距离为100 mm。发射探头和接收探头对向排列在缺陷的两侧,两探头与缺陷间的距离均为50 mm,发射探头的入射角为6.14◦,接收探头向相反方向倾斜6.14◦。检测试件为钢轨试件,在钢轨踏面上有宽度1 mm、深度不同的人工缺陷的试块(1 mm∼6 mm)和无缺陷钢轨踏面试块。

图5 仿真模型Fig.5 Simulation model

图6 导波在不同时刻在钢轨中的传播过程Fig.6 Propagation of guided waves in rail at different times

图7 检测钢轨踏面的摆放方式Fig.7 Detection of rail head placement

图8 实验环境Fig.8 Experimental environment
2.2 结果分析
使用非接触空气耦合超声波检测系统对钢轨轨头缺陷进行检测,实验结果如表1所示。图9为检测无缺陷钢轨轨头(图9(a))、3 mm缺陷钢轨轨头(图9(b))、6 mm缺陷钢轨轨头(图9(c))采集到的波形图。发射探头发射超声波,一部分超声波被缺陷反射,忽略其他衰减情况下另一部分超声波穿过缺陷并发生泄漏,在80µs左右时被接收探头接收,即承载有效缺陷信息的信号。接着,由于实际实验中发射探头与接收探头之间无真空板阻挡,超声波会由发射探头发射不经过钢轨从空气中直接到达接收探头,在100µs时被接收。从检测结果图9和图10可以得出:缺陷长度越大,被阻挡的超声波越多,绕过缺陷到达接收探头的超声波越少,进而波形图对应幅度降低。
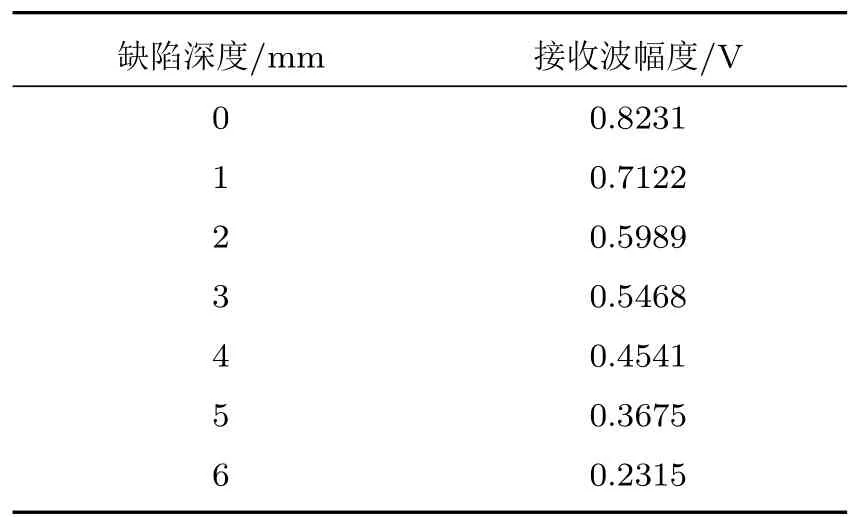
表1 不同深度缺陷的幅度结果Table 1 Amplitude with different depth defects results

图9 实验波形图Fig.9 Experimental waveform

图10 不同深度缺陷信号幅度曲线Fig.10 Amplitude curve of defect signal at different depths
3 结论
空气耦合检测技术由于不需要使用耦合剂,更容易用于在役检测,具有一定的研究价值。本文针对钢轨踏面现有的检测方式存在的不适合在役检测、操作不便、受环境因素较明显等问题,提出了以空气耦合超声波检测方法为基础的对钢轨踏面缺陷的检测方法。对钢轨模型的有限元和模态进行分析,并通过实验对无缺陷钢轨轨头、不同长度缺陷的钢轨轨头采集到的波形图所得结果进行分析,可知当钢轨轨头表面有缺陷时,接收到的信号幅度降低,并随着缺陷深度的增大而减小,能有效区分缺陷信号。以透射法为原理,主要从类瑞利波透过缺陷的幅度大小来判断缺陷特性,透射波幅度与缺陷有密切关系,但决定透射波幅度的因素很多,如换能器响应特性、钢轨材质和大小、换能器和钢轨的相对距离和方位等。因此,在实际检测时,需制定相关标准并使用标准试块对以上所述无关影响因素进行规定。

