铝板损伤的超声Lamb波与机磁阻抗集成检测
(大连交通大学 机械工程学院, 大连 116028)
超声Lamb波具有传播距离远、检测范围广、应用时间长、技术较为成熟等特点,可以很好地应用于板状材料的结构健康检测中[1-2]。Lamb波在板中传播时存在频散特性且模态复杂多样的特点,CAWLEY等[3]通过合理地选择窄带正弦激励信号来消除Lamb波频散效应的影响。结构健康检测的首要目的是对损伤进行定位。Lamb波遇到缺陷会发生散射等现象,散射信号包含了损伤位置、程度等信息,通过信号分析处理,可以实现损伤的定位和识别[4]。
机磁阻抗法是近几年才兴起的一种阻抗测量方法。ANDREI等[5]通过试验研究证明机磁阻抗可用于金属结构的多模态动态识别与诊断。TIMOTHY等使用机磁阻抗法监测铝合金的疲劳损伤,证明机磁阻抗法可用于早期疲劳损伤的检测。贾振元等[6]建立了超声磁致伸缩执行器的矢量阻抗分析模型,证明了模型计算的阻抗与试验测试的阻抗相近。笔者提出将超声导波和机磁阻抗技术结合在一起进行铝板结构的健康检测,并且提出一个融合机磁阻抗和超声导波数据的综合损伤指数,以指数的不同变化区间来对损伤类型和程度进行定性识别。
1 机磁阻抗集成超声导波的复合检测机理
机磁阻抗(MMI)检测是一种新兴的检测技术,其使用磁场取代传统电场的检测方法,且使用超高性能的超磁致伸缩材料,使得该检测方法比传统的机电阻抗法具有更高的灵敏度和能量转换效率。机磁阻抗检测机理本质上也是一种机械阻抗检测方法,与普通机械阻抗方法不同的是,机磁阻抗所采用的主动式传感器是通电线圈在磁场作用下基于涡流效应激励和接收弹性波的电磁超声换能器(EMAT),而EMAT也可用于超声Lamb波的激励和接收。EMAT在分别进行Lamb波与MMI激励接收时,其工作于不同的激励模式和接收模式,前者是用窄频带脉冲激励超声波,后者是用变频连续波信号激励受迫振动;前者是用EMAT接收Lamb波的回波信号进行缺陷分析,后者是对EMAT激励电路的阻抗受缺陷影响而导致的变化进行分析。
1.1 超声Lamb波检测原理
超声Lamb波检测时,铝板上传感器的分布方式如图1所示,坐标原点设在正方形铝板的左下角,d为损伤点,坐标为(x,y)。A,B,C,D为正方形的4个顶点,分别布置4个超声换能器,其到边界的距离为铝板边长的四分之一,坐标分别为(x1,y1),(x2,y2),(x3,y3),(x4,y4)。超声Lamb波检测时,由换能器EMAT1在点A激励一组超声Lamb波,由EMAT2,EMAT3,EMAT4采集相应的响应信号。

图1 超声Lamb波检测时铝板上传感器的分布方式
以Lamb波检测铝板时,可以通过4点圆弧定位法对板上缺陷进行定位。换能器接收到的经过缺陷散射后的信号减去无损状态下的基准信号,可得到只含缺陷信息的信号,即差信号。差信号时间延迟为
t=r1/cgH+r2/cgD
(1)
式中:r1为激励换能器到缺陷的距离;r2为接收换能器到缺陷的距离;cgH为未经过缺陷散射的波群速度;cgD为经过缺陷散射后的波群速度。
已知4个传感器的坐标分别为(x1,y1),(x2,y2),(x3,y3),(x4,y4)。损伤源坐标未知,设为(x,y),以EMAT1传感器为激励源,分别以EMAT2,EMAT3和EMAT4为接收传感器,接收到的差信号时间延迟t12,t13,t14分别为
上述3个方程只含有x,y和cgD3个未知量,因此联立式(2),(3)和(4)便可求出损伤位置坐标(x,y)以及cgD。
从3个接收换能器采集的响应信号中读取差信号的延迟时间,再通过式(1)进行计算,便可得到缺陷的位置坐标。
1.2 机磁阻抗检测原理
在机磁阻抗检测中,若要将铝板的机械阻抗表达成耦合体的电阻抗,需要先建立电磁超声换能器与铝板耦合后的矢量阻抗模型。通过耦合剂将磁致伸缩片和铝板耦合为一体,耦合体的截面结构示意如图2所示,其中线圈用于提供动态磁场,磁铁用于提供静态偏置磁场,磁致伸缩片为一圆形薄片,负责将振动传递给铝板。

图2 耦合体的截面结构示意
在自由应力状态下,根据式(5),磁致伸缩力可表示为
fM=-t(eTH)
(5)
式中:e=[eki]为逆压磁矩阵;H为磁场强度。
洛伦兹力是指非铁磁导体表面集肤深度内的受力,其大小由磁铁提供的静态偏置磁场和非铁磁导体表面的感应涡流共同决定,即
fL=B0×Je
(6)
式中:fL为洛伦兹力;B0为静态磁感应强度;Je为非铁磁导体表面的感应涡流。
则铁磁材料的总受力为
f=fM+fL
(7)
式中:fM为磁致伸缩力。
在洛伦兹力和磁致伸缩力的共同作用下,铁磁材料内质点位移的平衡方程为
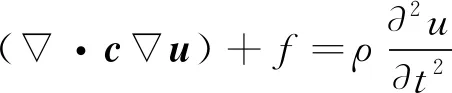
(8)
式中:c为刚度系数矩数;u为质点位移矩阵。
由材料的逆磁致伸缩效应,有
BM=eS
(9)
式中:BM为磁致伸缩材料质点位移引起的磁感应强度;S为应变张量矩阵。
则铁磁材料内的磁致伸缩电流密度为
JM=×BM
(10)
铁磁材料内运动的带电粒子在外加偏置磁场作用下产生洛伦兹电流,其电流密度为
JL=σν×B0
(11)
式中:σ为应力张量矩阵;ν为铁磁材料内带电粒子运动的速度矢量。
则铁磁材料内的总电流密度为
J=JM+JL
(12)
对接收线圈积分,则接收线圈和铁磁材料各区域所满足的控制方程为
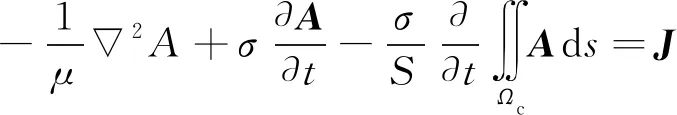
(13)
式中:μ为磁媒质的磁导率;A为磁致伸缩材料各区域的矢量磁位;Ωc为接收线圈横截面区域;s为横截面积;J为总电流密度矢量。
解上述方程可以求得各区域的矢量磁位,矢量磁位关于时间求偏导即可得到感应电场强度。则线圈导体内的感应电场强度可表示为
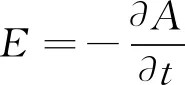
(14)
通过对电场强度线积分可得线圈中某点导体的电动势为

(15)
而线圈的电流又可以通过电流密度积分得到,即
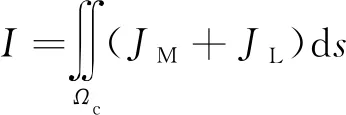
(16)
耦合体的动态机磁阻抗可表示为

(17)
铝板和磁致伸缩片的耦合体与换能器线圈之间的电磁相互作用可通过互感M进行等效转换。模型等效电路如图3所示,等效电路包括换能器线圈电感LM,换能器线圈电阻RM,磁致伸缩片电感LS,以及磁致伸缩片和铝板耦合后的动态机械阻抗ZS(ω)。在理想条件下,阻抗将是唯一表征结构动态特性的参量。分析该电路,可以得出机磁阻抗如式(18)所示。

(18)
式中:w为激励信号频率。
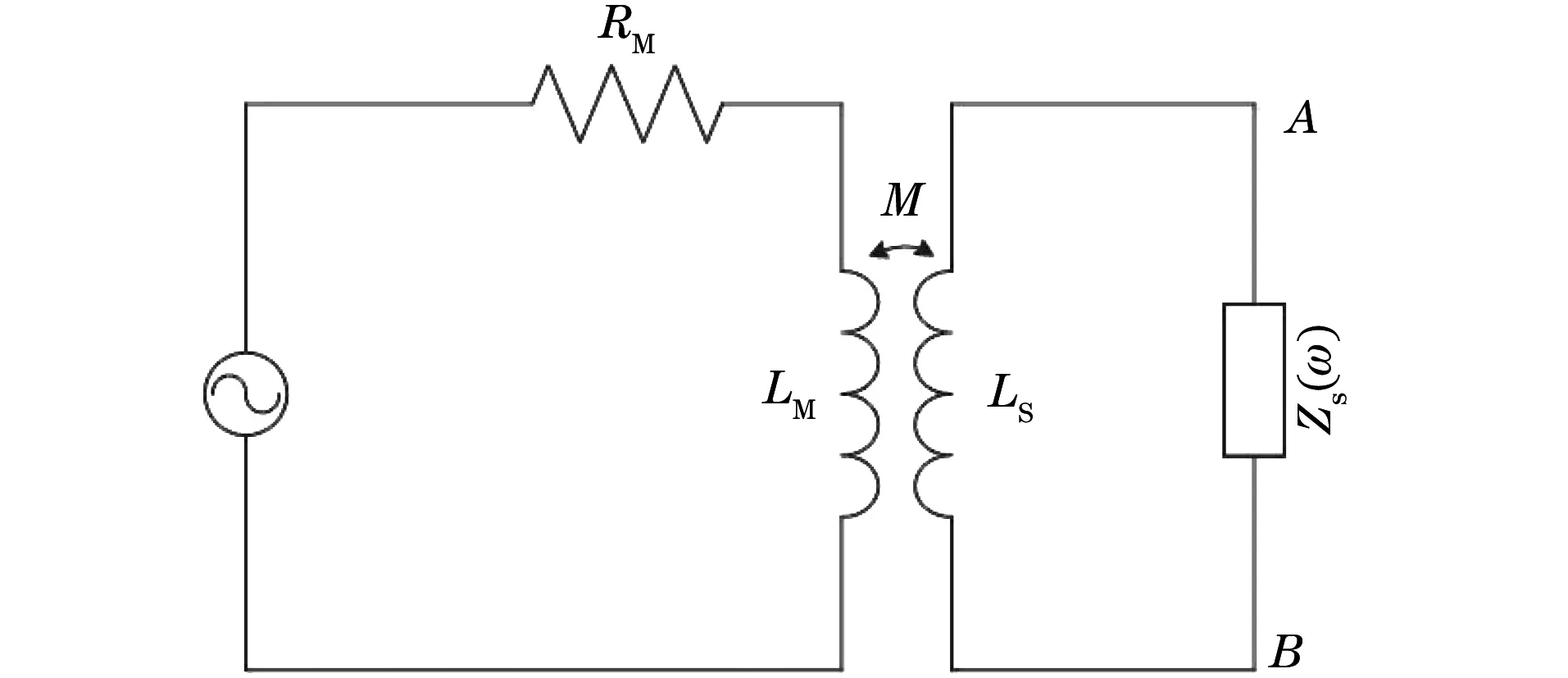
图3 模型等效电路
在式(18)中,负责磁电耦合的一个重要参数是M,该参数取决于材料、气隙和线圈参数设置等因素。为了方便建立模型,根据磁电耦合理论,提出一个从0到1变化的耦合系数kc来代替互感M。该耦合系数kc取决于线圈电感、磁致伸缩片电感以及互感。
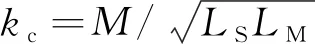
(19)
将式(19)代入式(18),即可得到机磁阻抗的最终表达式为
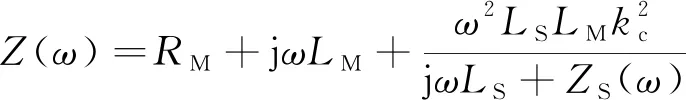
(20)
1.3 数据融合
将测得的导波信号和阻抗信号进行相关运算,并将得到的相关系数进行融合,得出一个新的损伤判别指标,以该损伤判别指标来定性识别缺陷。
此处,引入相关系数C对超声导波信号和机磁阻抗信号进行分析计算,相关系数是研究变量之间相关程度的量,用来表示超声导波信号或机磁阻抗信号受实际损伤影响而变化的程度,即结构变化的程度。其计算公式为
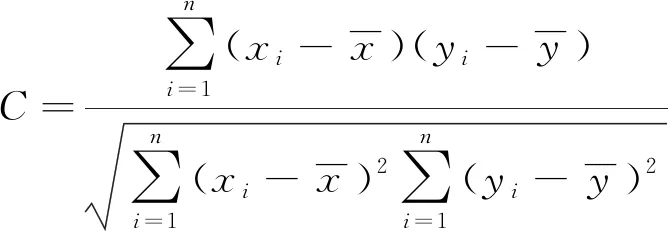
(21)
式中:xi,分别为不同损伤时数据及取n个点求得的平均值;yi,分别为无损时数据及取n个点求得的平均值。
这里的数据是指超声导波信号幅值以及机磁阻抗。为了更直观地表示相关系数与结构损伤之间的关系,损伤指数可用式(22)表示。
D=1-C
(22)
数据融合的步骤如下所述。
(1) 用x1(t)表示有损状态下测得的超声导波信号幅度,且测得带有缺陷信息的波包起止时间分别为t1和t2,在t1到t2时间内平均取n个点,并记录n个点处x1(t)的值,取平均求得;以y1(t)表示无损状态下测得的超声导波信号幅度,以同样的方式计算1。用x2(f)表示有损状态下测得的机磁阻抗,f1和f2分别表示起止频率,在f1到f2频段内平均取n个点,并记录n个点处x2(f)的值,取平均求得2;以y2(f)表示无损状态下测得的机磁阻抗,以同样的方式计算2。将得到的数据代入式(21)和(22),求出各自的损伤指数。
在某一特定路径上,将上述值含义直观解释为:x1(t)为有损状态下超声导波的信号幅值;1为有损状态下,在t1到t2时间内超声导波信号的幅值平均值;x2(f)为有损状态下的机磁阻抗幅值;2为有损状态下,在f1到f2频段内机磁阻抗幅值的平均值;y1(t)为无损状态下超声导波信号幅值;1为无损状态下,在t1到t2时间内超声导波信号幅值的平均值;y2(f)为无损状态下机磁阻抗的幅值;2为无损状态下,在f1到f2频段内机磁阻抗幅值的平均值;
(2) 引入一个比例因子,通过比例因子将这2种方法得到的损伤指数进行融合,比例因子要能反映2个损伤指数在综合损伤指数中所占的比重。比例因子k的表达式为

(23)
式中:DGUW(i)为超声导波路径i上的损伤指数;nGUW为超声导波传播路径的个数;DMMI为机磁阻抗节点A处的损伤指数。
(3)DGUW(1),DGUW(2)和DGUW(3)为超声导波传播的3条路径上的损伤指数,DMMI为机磁阻抗检测节点A处的损伤指数,D1-A,D2-A和D3-A为综合损伤指数。综合损伤指数的计算公式为
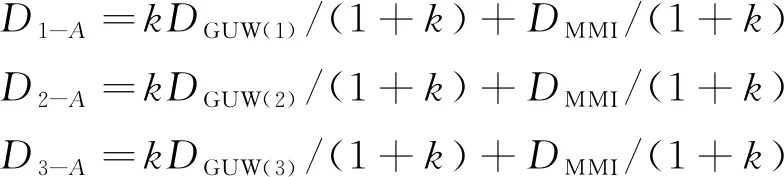
(24)
(4) 将得到的综合损伤指数结合损伤类型和程度绘制成图,通过比较综合损伤指数的大小,即可实现损伤类型和程度的识别。
2 Lamb波检测仿真
在试验研究中,对于测试获得的信号,需要调理电路对信号进行处理,将环境噪声过滤掉。因此,可以采用仿真来近似模拟无噪声影响的理想情况。为了真实反映实际测量情况,对换能器与铝板之间的耦合场进行建模。采用ANSYS软件瞬态动力学模块进行建模和分析。仿真过程中,铝板和换能器的参数设置分别如表1和表2所示。

表1 铝板参数

表2 换能器参数
建立仿真模型,A,B,C,D点坐标分别为(420,420),(420,780),(780,780),(780,420),设置缺陷位置坐标为(615,615)。为了减少Lamb波频散现象,方便对结果进行分析和处理,使用5个周期汉宁窗调制的正弦信号进行激励。选择激励信号中心频率为250 kHz,可以激励出单一的S0或A0模态波形,仿真时选择S0模态波形进行研究。建立无损和有损两类模型,其中一个模型作为标准模型,模拟无损标准铝板,剩下的模型均设置一个缺陷,通孔直径分别为5,7,9,12,15,17 mm。
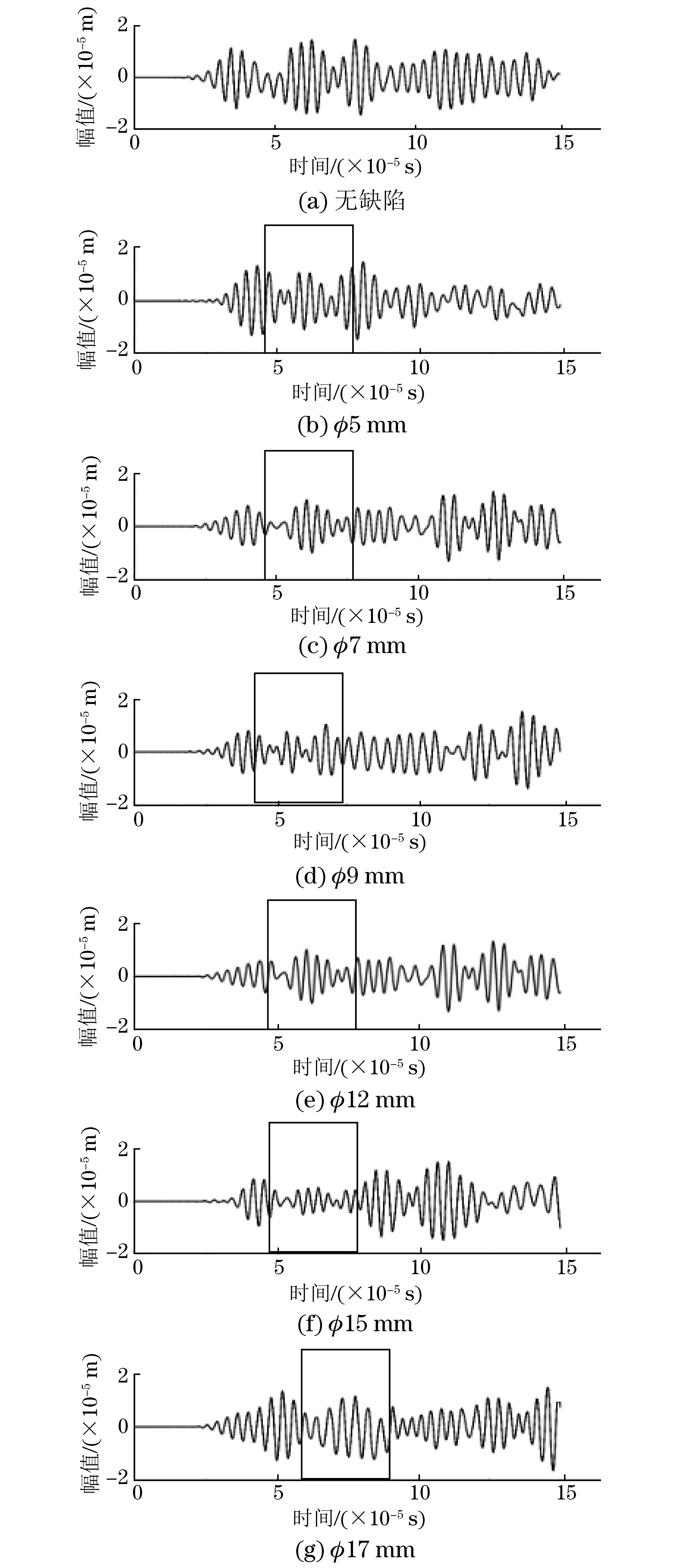
图4 带有不同直径通孔缺陷的铝板上的B点波形

图5 带有不同直径通孔缺陷的铝板上的C点波形
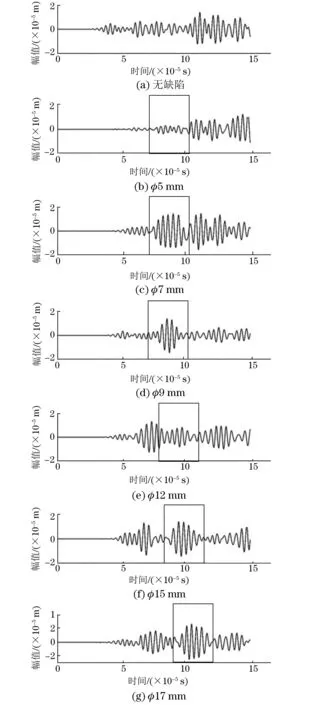
图6 带有不同直径通孔缺陷的铝板上的D点波形
分别记录无损和有损铝板在B,C和D三点的响应信号波形,并将不同直径通孔缺陷的波形并列显示于图中。在仿真过程中,铝板的厚度为2 mm,激励信号的频率为250 kHz,因此频厚积为0.5 MHz·mm。此时,板中传播的Lamb波只含有S0和A0模态。由于S0模态波包的传播速度大于A0模态波包的,所以图中可以观察到S0模态波包在前,A0模态波包在后。在图46中,第一个波包为S0模态直达波包,第二个波包为经过缺陷散射以后的S0模态波包,需要的是第二个波包的到达时间。关于到达时间的读取,采用MATLAB软件寻找响应信号波形中第二个波峰所对应的时间,即寻找第二个波包幅值最大点所对应的时间,可通过与基准信号相减,去除直达波、边界反射波等的影响,剩下的波包即为只含缺陷信号的波包,可直接读取波包幅值最大点所对应的时间。
带有通孔缺陷的铝板在B,C,D三点的响应信号波形如图46所示。
从图46中读取第2个S0模态波包的到达时间,并将时间代入式(1),通过文中所述4点定位法进行计算,得到通孔缺陷的坐标如表3所示。建模所设损伤点d的坐标为(615,615),对比可知,超声导波检测可以实现损伤的准确定位。
将图46中的超声导波数据平均取点,并求得无损和有损两种状态下的平均值,代入式(21)和(22),计算得到带有不同孔径通孔缺陷铝板的3条路径的损伤指数如图7所示。
由图7可知,在3条导波传播路径上,损伤指数与损伤程度成正比关系,即损伤指数随损伤程度的增加而增加。
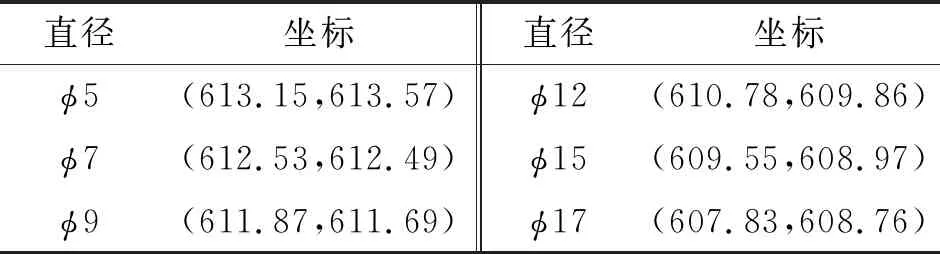
表3 不同直径通孔的坐标 mm
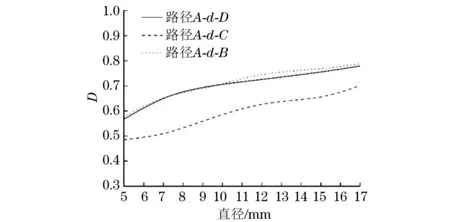
图7 不同直径通孔缺陷铝板的3条路径的损伤指数
3 机磁阻抗检测仿真
机磁阻抗检测采用ANSYS软件谐响应模块进行建模和分析,找到机磁阻抗随频率变化的关系。分析过程中只计算结构的稳态受迫振动,不考虑激振开始时的瞬态振动。谐响应分析的目的在于计算出结构在不同频率下的响应值对频率的曲线,从而预测出结构的持续动力特性。
谐响应分析几何模型与导波仿真所用几何模型相同,参数设置以及边界条件均一样。但是,谐响应分析所用激励信号是另外一组信号,信号为频率从240 kHz到241 kHz的正弦调频信号。激励方式也不同,谐响应分析时,需要用调频信号激励图1中的A点,并在A点收集铝板的响应信号。
随着缺陷程度的增加,共振点的频率和幅值均发生了变化。将不同程度损伤测得的机磁阻抗图中的数据平均取点,求得有损和无损两种状态下的平均值,代入式(6)和(7),计算出损伤指数D与通孔直径的关系曲线如图8所示。
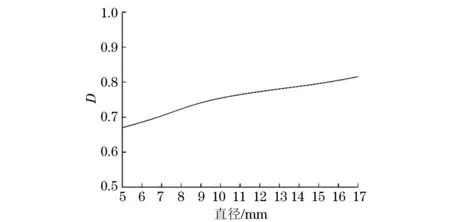
图8 通孔缺陷损伤指数与通孔直径的关系曲线
由图8可知,对于同类缺陷,损伤指数和损伤程度成正比的关系,即损伤指数随损伤程度的增加而增加。因此,损伤指数的数值差异可用于损伤程度的识别。
4 综合损伤指数计算及结果讨论

图9 3条路径的损伤指数、综合损伤指数与通孔直径的关系曲线
综合损伤指数是将两种检测方法得出的损伤指数进行融合生成的。首先,通过式(8)计算比例因子k,比例因子反映了通过两种测试方法得出的损伤指数所占的比重。然后,结合比例因子k,将超声导波法和机磁阻抗法得出的损伤指数通过式(9)进行结合,求得综合损伤指数。图9为通过超声导波信号幅值所求的3条路径的损伤指数、综合损伤指数与直径的关系曲线,各分图中下面的曲线为超声导波测试得到的损伤指数曲线,上面的曲线为综合损伤指数曲线。
图9显示了在不同路径下,综合损伤指数和通孔直径的关系。由图9可知,综合损伤指数与损伤程度成正比的关系,即损伤程度越大,综合损伤指数也越大。因此,该综合损伤指数可以用于损伤程度的识别,可明显看出综合损伤指数曲线的线性度高于单纯通过导波计算得出的损伤指数,损伤尺寸越小,线性度对比越明显。
5 结论
在仿真分析中,研究了厚度为2 mm铝板在5个周期汉宁窗调制的正弦信号以及频率为240 kHz~241 kHz的调频信号激励下的响应。研究表明,机磁阻抗结合超声导波的复合检测方法能得到比两种方法单独使用时更全面的检测结果,对于铝板上设置的不同大小的通孔缺陷,超声Lamb波检测可以对缺陷进行准确定位。为了进一步得到更多的损伤信息,对不同状态的铝板进行了机磁阻抗分析,结果表明机磁阻抗谱数值上的差异更易于识别损伤的程度。对超声导波图谱和机磁阻抗图谱分别进行换算,得出各自的损伤指数,将这些损伤指数进行数据融合得出一综合损伤指数,该综合损伤指数的不同变化区间可以用于铝板结构损伤程度的识别。将超声导波和机磁阻抗两种技术结合起来应用于铝板结构的健康检测,可以有效获得损伤的位置、程度等状态信息。

