APU二级涡轮叶片疲劳寿命计算与分析

王航超

(沈阳航空航天大学 民用航空学院，沈阳 110136)

APU(Auxiliary Power Unit，APU)辅助动力装置是一台小型的燃气涡轮轴发动机，一般安装于飞机最后段的尾椎之内，由动力段、负载压气机和附件齿轮箱等三大部分组成，主要作用是给飞机提供电力和压缩空气。陈龙等[1]采用了名义应力法并结合ANSYS软件分析计算了斗齿结构的疲劳寿命。杨志凌等[2]采用CAE模拟技术计算了风电机组齿轮的疲劳寿命，并与其理论计算年限作比较，验证了该方法的合理性。高振山等[3]采用弹塑性有限元模型，对弧齿锥齿轮热锻成型的模具应力分布进行了仿真并基于应力应变法分析了各工艺因素对模具寿命的影响规律。熊伟红等[4]采用局部应力应变法估算起重机钢丝绳的疲劳寿命，并结合有限元法验证了其合理性与可靠性。本文采用CATIA软件对APU二级涡轮组件进行三维建模，然后使用ANSYS Workbench软件建立叶片有限元模型，再通过CFX、多场耦合模拟仿真，获得叶片的应力、应变云图，确定叶片危险部位，最后基于有限元模拟仿真，通过Manson-Coffin公式计算出叶片疲劳寿命、预测叶片疲劳寿命。利用Fatigue Tool软件仿真，验证了这一局部应力应变预测方法所得结果的合理性与可行性。研究结果为设计人员设计、优化叶片叶型奠定了基础，为APU维修人员监测叶片寿命状态提供参考。

1 APU二级涡轮组件三维建模

APU二级涡轮组件由三十一块叶片与涡轮盘装配而成。基于CATIA的“零件设计”模块分别完成叶片、涡轮盘的三维建模，并在“装配设计”模块完成装配，APU二级涡轮组件三维模型图如图1所示。

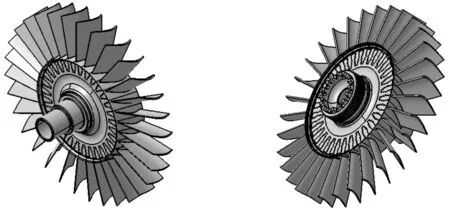
图1 APU二级涡轮组件三维模型图

2 叶片有限元应力应变分析

2.1 前处理

APU在正常(稳定)工况下，高温高压燃气冲击叶片，温度场、压力场遍布于叶片表面，主轴旋转产生离心力。通过ANSYS Workbench中CFX模块完成叶片流场分析与计算，在Static Structural模块中对叶片的流-热-固耦合作用进行仿真，有限单元法分析流程图如图2所示。

图2有限单元法分析流程图

图3叶片有限元模型图

叶片模型从CATIA中导入，叶片材料为GH4133B镍基变形高温合金，在Engineer Data中添加材料参数，叶片网格采用Solid187单元(10节点四面体单元)，单元尺寸为0.5 mm，单元数58837，节点数103655，叶片有限元模型图如图3所示。热载荷、气动载荷从CFX分析结果中导入，APU的循环工作状态“起动-最大(恒速)-起动”，涡轮叶片的恒定转速为49300 rpm，在Rotational Velocity中设置转速为绕X轴-821.66 rad/s。实体单元有且仅有三个移动自由度，根据叶片与涡轮盘的实际装配和工作情况，叶片榫头底面施加固定端约束(Fixed Support)以限制轴向运动，榫头榫槽面施加位移约束(Displacement)分别限制径向、周向运动[5-7]。

2.2 后处理

计算完成后，得出叶片等效应力云图和叶片等效应变云图分别如图4、图5所示。

图4叶片等效应力云图

图5叶片等效应变云图

分析图4，叶背应力水平总体高于叶盆，叶根部应力明显较大。APU从起动状态n=0 rpm到最大(稳定)状态n=49300 rpm两载荷步时，最大应力为σmax=832.93 MPa，位于叶片前缘根部，最小应力为σmin=0 MPa(APU静止状态n=0 rpm)，叶片应力幅值σa和平均应力σm为：

3 叶片疲劳寿命计算与分析

3.1 疲劳寿命计算方法

按照构件所承受循环应力大小，疲劳一般可分为应力(高周)疲劳和应变(低周)疲劳。如果最大循环应力σmax小于屈服应力σs，称为应力疲劳，如果最大循环应力σmax大于屈服应力σs，则材料屈服后应变变化比较大，应变作为疲劳控制参量，称为应变疲劳。目前，名义应力法、局部应力应变法和应力场强法为工程中比较常用的三种疲劳分析法。根据上一节有限元等效应力分析结果可知，APU从起动状态到最大(稳定)状态两载荷步时，叶片所承受的最大应力高于GH4133B材料700 ℃时的屈服应力为716 MPa，对应的变形为弹塑性变形，属于高应力低频疲劳状态。名义应力法不考虑局部塑性变形，导致疲劳寿命预测精度和可靠性会大大降低；局部应力应变法一般用于缺口件在低周疲劳下的裂纹萌生寿命，所以本文采用局部应变法进行疲劳寿命预测是合理可行的。局部应力应变法寿命预测流程图如图6所示。

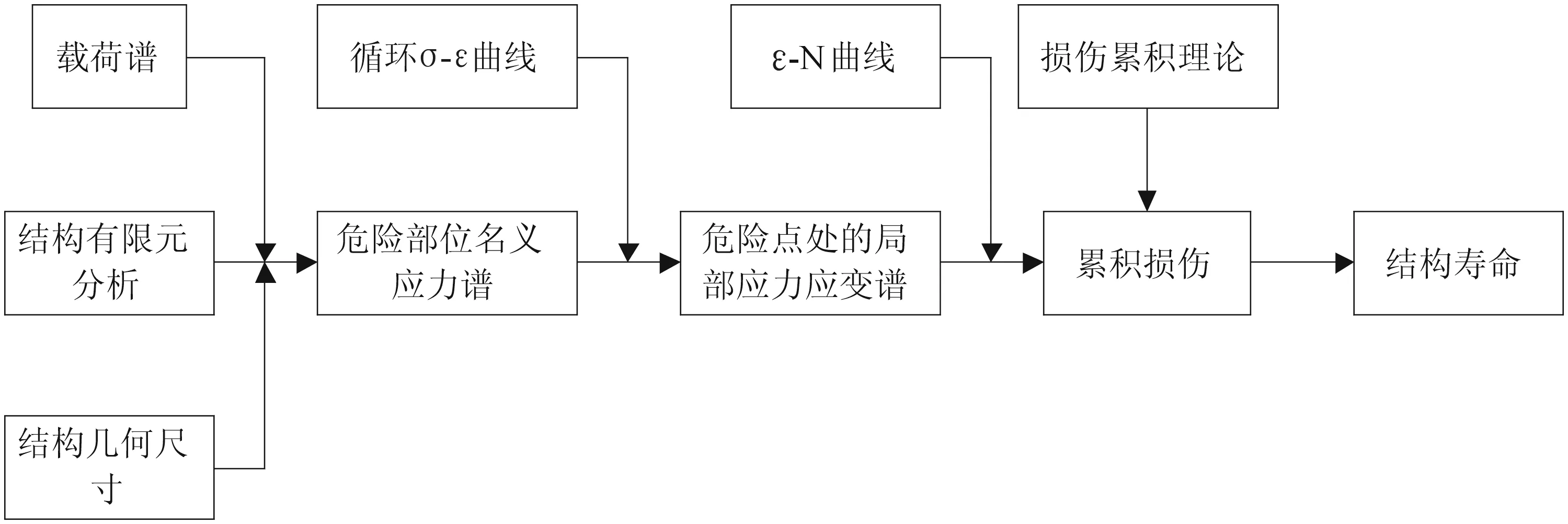
图6 局部应力应变法寿命预测流程图

3.2 Manson-Coffin模型

局部应力应变法中的应变-寿命(ε-N)曲线描述了结构件应变与疲劳寿命之间的关系。在众多的ε-N曲线中，Manson-Coffin模型被学者们认可，在工程中也被广泛应用。此模型综合考虑了高周应力疲劳和低周应变疲劳，其数学表达式为：

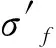
实际载荷作用时，基本不存在对称循环，但是实际载荷的幅值和均值均会对疲劳寿命预测产生偏差。基本的Manson-Coffin模型只针对对称循环下应变与寿命之间的关系。对于非对称循环，如果采用Manson-Coffin模型预测结构件疲劳寿命，需要做平均应力修正。Morrow总应变修正的Manson-Coffin数学表达式为：

其中，σm为平均应力，其他均为材料常数[8-9]。

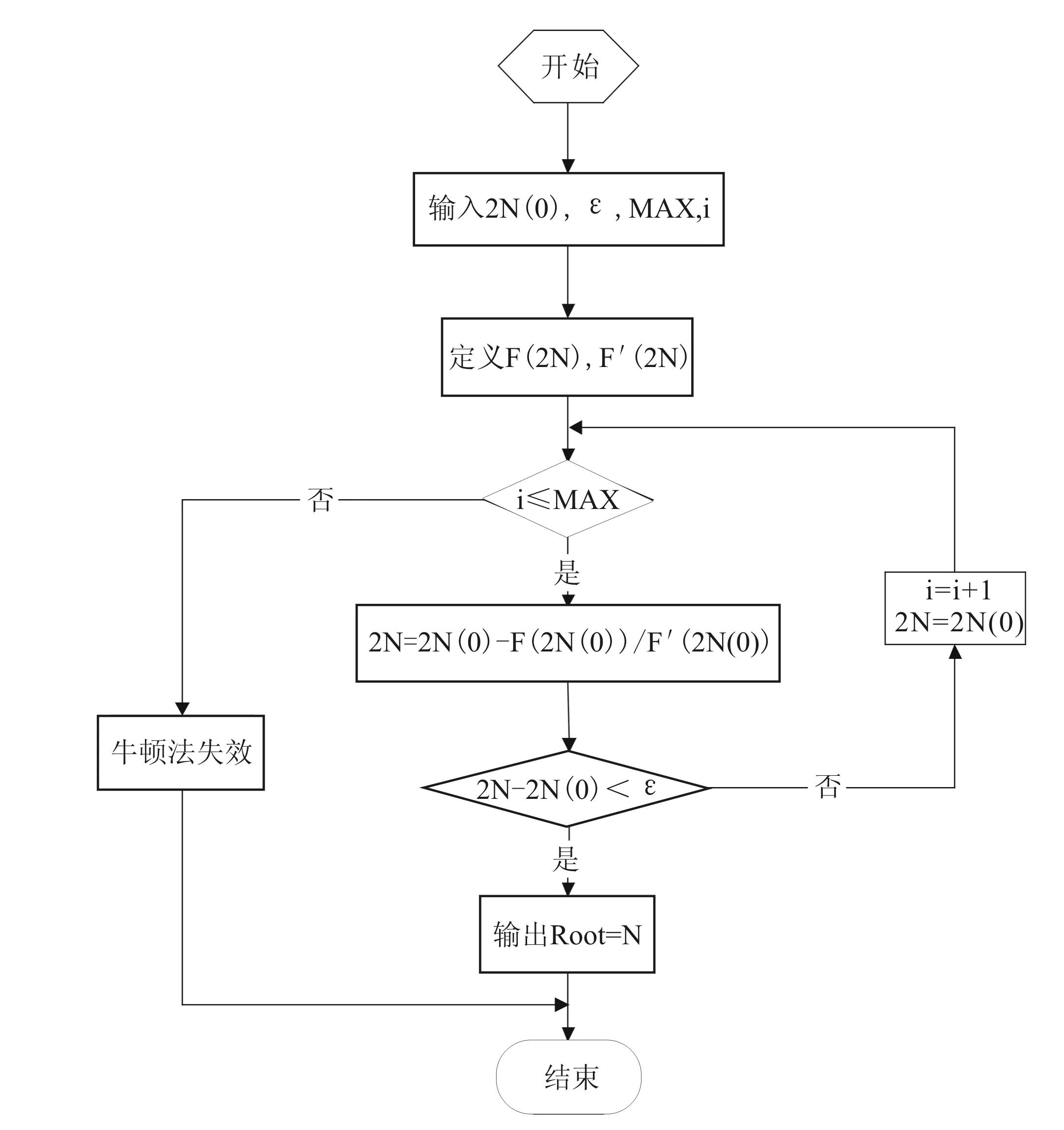
图7牛顿迭代法MATLAB计算流程图

3.3 Newton迭代法

Morrow总应变修正的Manson-Coffin模型为非线性方程，无精确解。因此，文中采用牛顿迭代法解析此方程。牛顿迭代法是一种近似求解的方法，牛顿迭代法思想：非线性方程f(x)=0近似转化为线性方程求解。牛顿迭代法MATLAB计算流程如图7所示。

Morrow总应变修正的Manson-Coffin模型对应的牛顿迭代法计算如下：

F(2N)导函数：

牛顿迭代法：

取2N(0)=1，收敛条件

|2N(i+1)-2N(i)|≤0.01

(6)

3.4 疲劳寿命计算

Manson-Coffin模型中的材料参数直接、准确的获取方式是疲劳试验，也可以通过查材料手册获取。文中GH4133B材料在手册中可以查到600 ℃疲劳性能参数，而APU二级涡轮入口温度接近700 ℃，所以采用GH4133B材料基本性能参数和“改进通用斜率法”来估算其对应温度下的疲劳性能参数，改进通用斜率法如表1所示。

表1 改进通用斜率法

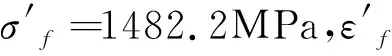
3.75×10-3=0.719×[9.30×10-3(2N)-0.09+0.2876(2N)-0.56]

(7)

表达式(7)为非线性方程，采用MATLAB牛顿迭代法编程计算疲劳寿命N=5103次。

基于ANSYS Workbench中的Fatigue Tool计算叶片应力循环次数为5244次，叶片疲劳寿命云图如图8所示，与局部应力应变法Manson-Coffin公式计算结果仅相差3%，说明局部应力应变法计算叶片疲劳寿命具有可行性[10-15]。

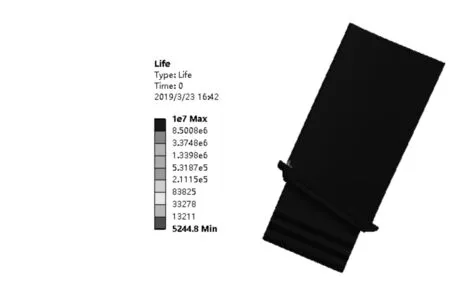
图8叶片疲劳寿命云图

4 结论

(1)通过采用ANSYS Workbench对 APU二级涡轮叶片正常工作状态的模拟仿真可知，叶背应力水平总体高于叶盆，叶根部应力明显较大，最大应力处于叶片前缘根部，大小为832.93 MPa，最小应力处于叶片后缘顶部，大小为0.016 MPa。

(2)通过对比APU二级涡轮叶片局部应力应变法Manson-Coffin模型预测结果和Fatigue Tool仿真结果，误差率为3%，证明了Morrow总应变修正的Manson-Coffin模型预测APU二级涡轮叶片疲劳寿命的合理性，确定了APU二级涡轮叶片Manson-Coffin疲劳寿命预测模型为：

εα=0.719×[9.30×10-3(2N)-0.09+0.2876(2N)-0.56]

(3)基于局部应力应变法的APU二级涡轮叶片从起动到恒定转速的两载荷步时的疲劳寿命为5103次。