基于倒向随机微分方程的光纤陀螺稳定性评估方法

秦伟亮，魏法杰

（北京航空航天大学 经济管理学院，北京 100191）

光纤陀螺是一种基于Sagnac原理的纯固态惯性仪表，具有环境适应性好、可靠性高、寿命长、综合性能优等特点[1]，较适合应用于空间领域。国外公开报道光纤陀螺产品寿命已超过15万小时，国内光纤陀螺在卫星中连续工作时间也已超过数万小时。目前光纤陀螺已在商业卫星、军用卫星等领域取得了较广泛应用。但由于空间环境的特殊性，光纤陀螺性能指标会随着通电时间的积累而逐步退化[2]，进而影响到卫星的使用寿命。光纤陀螺在空间环境条件下的参数稳定性和卫星服役的匹配性，已日益成为光纤陀螺竞争力的一个重要表现。如果陀螺寿命远超过卫星寿命，则陀螺成本相对会高，竞争力降低；如果陀螺寿命达不到卫星寿命要求，则直接影响卫星使用。因此，开展对光纤陀螺参数稳定性的评估，以及对宇航光纤陀螺出厂指标参数进行控制的课题研究，对光纤陀螺的质量控制和推广应用有较强的意义。

当前，对宇航光纤陀螺的评估主要集中在可靠性和寿命评估等方面，所采用的主要方法是地面等效寿命试验或加速寿命试验，并利用数理统计方法对产品剩余寿命进行预测，进而得出产品的指标首达设定阈值时的稳定性时间分布[3]。

目前研究的特点是：根据光纤陀螺在空间环境条件下的退化机理，建立产品的退化模型，并通过试验数据和仿真求解模型参数，利用参数和产品性能退化的首达时间获得产品寿命估计。这是一种随时间变化的正向评估方法，可用于光纤陀螺在出厂后预期寿命的后评估。但正向评估方法的周期较长、经济代价较大，不适合于对每只使用的光纤陀螺都进行评估。基于此，本文在评价方法上采取新的途径：依据光纤陀螺在空间环境条件下的退化机理，通过引入倒向微分方程的理论，建立了相应模型，并通过模型求解，实现对产品的性能变化特征进行评估，实现对出厂参数进行控制，使其参数稳定性同卫星寿命相匹配。

1 倒向随机微分方程基本理论

倒向随机微分方程概念最早是由法国随机控制和随机分析专家Bismut[4]在1978年研究随机最优控制过程中提出来的。Bismut提出的概念是与正向系统方程相对偶的线性倒向随机微分方程。1990年我国学者彭实戈院士（Peng）和法国学者Pardoux共同提出了非线性倒向随机微分方程，并证明了其解的存在唯一性[5]。此后，倒向随机微分方程的研究取得了长足的进步，在随机控制、金融数学、递归效用和风险敏感效用等领域获得了广泛应用。

为引出倒向随机微分方程，先对比分析在区间[0,T]上正向和倒向常微分方程形式：

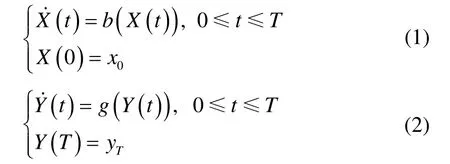
式中，b(·)、g(·)是给定的函数；x0、yT是给定的参数。

式(1)的定解条件在初始时刻T=0时刻给出，称它为正向常微分方程。式(2)的定解条件在终了时刻t=T时刻给出，称它为倒向常微分方程。

引入随机因素，即建立正、倒向随机微分方程。两者对比，其结构形式为：

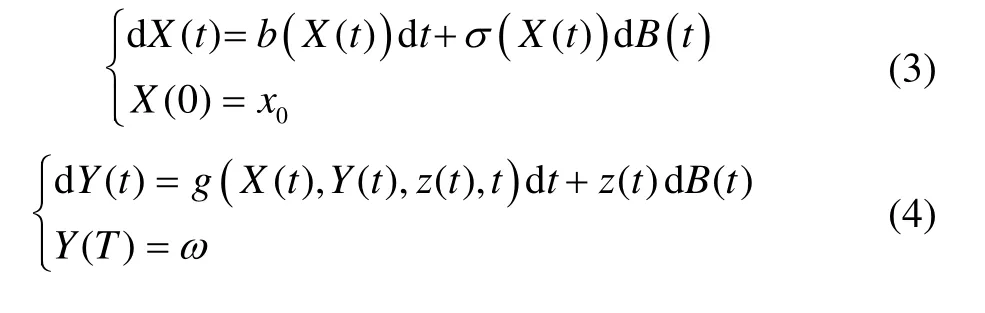
式(3)是正向随机微分方程，式(4)是倒向随机微分方程基本形式。两式联立，构成了一组正倒向随机微分方程组，其中，b(·)、g(·)、σ(·)、z(·)是给定的函数。

在数学上，分析求解随机微分方程一般需要测度论知识。(Ω,Ft,Pt)是一个含有信息流Ft的完备概率空间，Ft是由(Bs,s≤t)生成的σ代数，即Ft=σ(Bs,s≤t)，Bt是Ft上的标准的 Brown运动，Pt是概率空间上的概率测度。在式(4)中，ω是一个确定的可测得值，X(t)是状态变量，Y(t)和z(t)是倒向随机过程中同时间t相关的、需要同时解决的两个随机过程。g（X(t) ,Y(t) ,z(t) ,t）是倒向随机微分方程的生成元，是关于t、X(t)、Y(t)、z(t)的函数。

在工程实际上，一般过程都满足理论要求条件：给定时间区间[0,T]上，随机过程连续平方可积且有界，也即Y(t)、z(t)都是连续平方可积且有界的。在符合该条件时，正、倒向随机微分方程都满足解的存在唯一性[5]。

倒向随机微分方程解得存在唯一性和生成元表示定理奠定了倒向随机微分方程的理论基础。Pardoux-Peng[6]建立的非线性Feynman-Kac公式，将求解生成元中的Y(t)和z(t)随机过程与一个拟线性偏微分方程组的解建立了关系，从而获得倒向随机微分方程的唯一解表示。在工程应用上，Y(t)是可观测的随机过程，z(t)可用数学期望形式表示为：

式中，Δ表示为采样时间间隔，为条件数学期望，O(Δ)为Δ的高价小量。为便于表达，式中及下文将Y(t)简化表示为Yt，X(t)表示为Xt，z(t)表示为zt。

从式(5)中可以看出，z(t)的含义是Y(t)波动特性的表示。

与正向随机微分方程相比，倒向随机微分方程在结构上有较大不同，它们的主要区别和联系表现在：

1）正向随机微分方程有两个决定函数b(·)和σ(·)，其解是个随机过程X(t)，而倒向随机微分过程是由生成元g(X(t),Y(t),z(t),t)决定，它的解是一组随机过程Y(t) ,z(t)；

2）正向随机微分过程关注如何认识一个客观存在的随机变化过程，而倒向微分方程关注在随机干扰条件下如何使一个产品或系统达到预期的要求，也就是通过将来时刻给定的一个目标值来获得当前（产品出厂）时刻的值。正向随机微分方程的值代表今天确定的值变为明天一般不确定的状态以研究其统计规律，而倒向随机微分方程的值则表示将明天的目标变成今天的解以制定今天的决策[6]。

3）为了获得倒向随机微分方程的解，可建立一组正倒向随机微分方程组。根据随机最优控制理论和最大值原理，正向随机微分方程描述了系统的状态方程，引入一类倒向随机微分方程可作为状态方程的伴随方程，共同形成一组正倒向随机微分方程组[7]。通过对方程组的求解获得倒向随机微分方程的值。

2 光纤陀螺倒向微分方程模型

2.1 基本模型

目前，在卫星领域应用的光纤陀螺一般采用干涉式闭环信号处理方案，它在卫星环境条件下的性能退化特性在统计上可用随机维纳过程描述。光纤陀螺光源作为有源器件，其输出功率稳定性和噪声特性直接影响到陀螺的参数稳定性[2]，在陀螺的性能退化和寿命评估中具有重要作用。对光源输出功率和噪声的动力学特性分析表明，在稳态条件下的均匀介质中，光量子的运动轨迹是个马尔科夫过程，其输出功率和噪声特性符合Langevin模型。

Langevin模型是一个正向随机微分方程，其一般的方程表达式为：其中，X(t)是状态变量，μ和σ是状态变量的漂移系数和扩散系数，B(t)是标准的Brown运动。在描述光源的输出特性时，X(t)就表示光源的光功率，μX(t)表示光功率的随机漂移特性，σdB(t)表示光功率的噪声特性。

由式(6)可以看出，Langevin模型中变量X(t)的输出特性同X(t)随时间的变化率相关（在工程上也可理解为同变量的前一时刻X(t- 1 )的特性相关），这是同随机维纳过程模型的最大差别。

同光源的输出特性模型相比，干涉式闭环光纤陀螺的输出特性较复杂，影响因素较多，尚没有统一的动力学模型。但从光纤陀螺数理统计分析和可靠性研究角度，参照文献[3]所提到的研究方法，可以对陀螺的输出状态进行解析，选择陀螺静态条件下的输出特性进行研究，以反映陀螺自身特性变化引起的输出性能变化。本文选择在常温环境下陀螺的零位输出状态特性进行研究。

干涉式闭环光纤陀螺在工程实现上，是利用当前时刻和前一时刻的光源干涉强度差来实现闭环和信号处理输出的。借鉴光源输出的动力性模型，我们将陀螺的零位输出特性归纳为Langevin方程模型，是符合逻辑和工程特性的，但模型的具体符合度还需要利用数据进行检验和验证。因此本文以Langevin方程为基础，以光纤陀螺理论零位输出为状态变量，构建其状态方程。以状态方程为基础，下一步的重点是找到其伴随方程，完成正倒向随机微分方程组的建立。

构建倒向随机微分方程，尚没有工程模型可以直接借鉴引用。按照倒向随机微分方程理论，生成元函数g(X(t),Y(t),z(t),t)的构成形式决定了倒向微分方程的模型。但在理论上，非线性方程的生成元结构非常复杂，没有通用的模型可直接引用，因此若要建立光纤陀螺的倒向微分方程，只能从方程的机理和工程实际过程入手，构建相应模型并对模型进行检验验证。

由生成元g(X(t),Y(t),z(t),t)特性可知，Y(t)和z(t)是同倒向微分方程的解相关联的两个随机过程，z(t)是Y(t)波动特性的反应，X(t)是状态变量，而Y(t)是可观测的。另外我们建立光纤陀螺倒向微分方程的目的，就是在输出波动的情况下（波动是由于陀螺应力变化、环境影响及测试干扰等造成的），利用未来的陀螺零位值确定当前的零位值。因此将陀螺实际零位Y（t）作为方程的输出参量，将生成元g(X(t),Y(t),z(t),t)线性化，设为陀螺状态变量X(t)的线性函数，即Y(t) =atX(t) +bt，（其中at为权重系数，bt为同步偏差），就可完成方程的设立。

通过上述设定，其正倒向随机方程组的数学模型为：

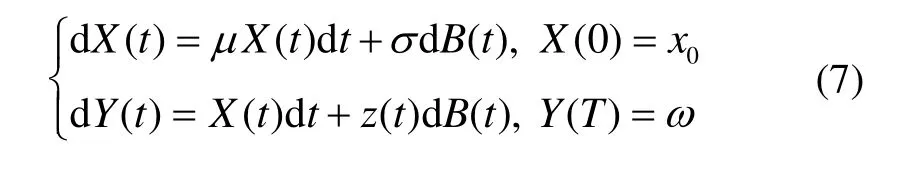
其中，X(t)为光纤陀螺的理论零位，是方程组的状态变量；Y(t)是光纤陀螺的实际零位，是输出变量；μ和σ是状态变量的漂移系数和扩散系数，μX(t)是陀螺零位漂移的趋势项，σdB(t)是陀螺零位的扩散项，二者都反映了陀螺零位变化的固有特征；z(t)是陀螺的波动特性反映，由陀螺的应力变化、环境影响及测试干扰等导致。

方程组在工程上的含义为在随机波动情况下陀螺实际零位同陀螺理论零位之间的函数关系特性。

2.2 模型求解

根据模型(7)，光纤陀螺的零位输出变量Y(t)和状态变量X(t)满足线性关系Y(t) =atX(t) +bt（其中at、bt为待求系数，设初始值a1= 1 ，b1= 0 ），且终端条件Y(t)=ω已知。为便于方程推导，不失一般性，对时间尺度归一化，设T= 1 。

当t∈[0 ,T]，利用Itô公式，可得出Y(t)关于X(t)的表达式[8]。

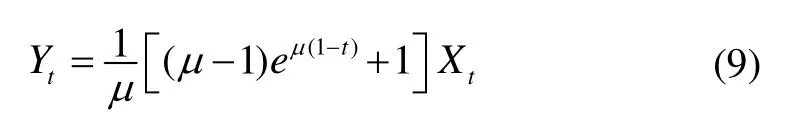
利用式(8)(9)，将对方程组的求解转化为对下列随机微分方程的参数μ和σ进行估计。

2.3 模型参数估计

对模型参数估计，需要获得产品在一定时间内的测试数据。对陀螺采样测试时间进行归一化，得到在时刻陀螺的测试采样数据，设0 ≤s≤t≤1，

利用Itô公式，可推导出给定tY和sY的条件分布为[8]：

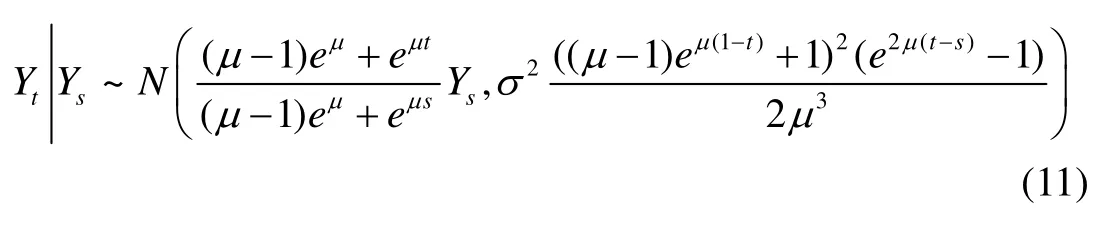
式中，N（·）是个标准的正态分布。

对所有1 ≤k≤n，将陀螺输出采样数据简化表示为用下列简化符号表示：

本文采用最大似然估计法对参数进行估计。根据式(15)，关于观测值的似然函数表达式为：

其中，转移密度函数为：

文献[8]证实了利用最大似然估计法所获得的正倒向随机微分方程估计参数具有强收敛性。在工程上，利用采样数据，就可根据最大似然估计法获得参数最优估计，并可利用估计参数计算模型的结果，同实际数据相比对，用来验证模型的正确性。

3 数值计算和应用

3.1 光纤陀螺采样数据获取

为了验证光纤陀螺在卫星上长期通电的参数稳定性，我们在长寿命试验室抽取同一批次的若干只陀螺进行了长期稳定性测试试验，并按照测试规范，逐月对陀螺的零位进行测试，表1是其中一只陀螺近9年的零位稳定性测试数据汇总。

为验证光纤陀螺正倒向随机微分方程模型的正确性。在数据处理上，先利用 2009～2014年的数据对模型参数进行估计，然后再用2015～2019年数据对模型参数进行交叉验证。

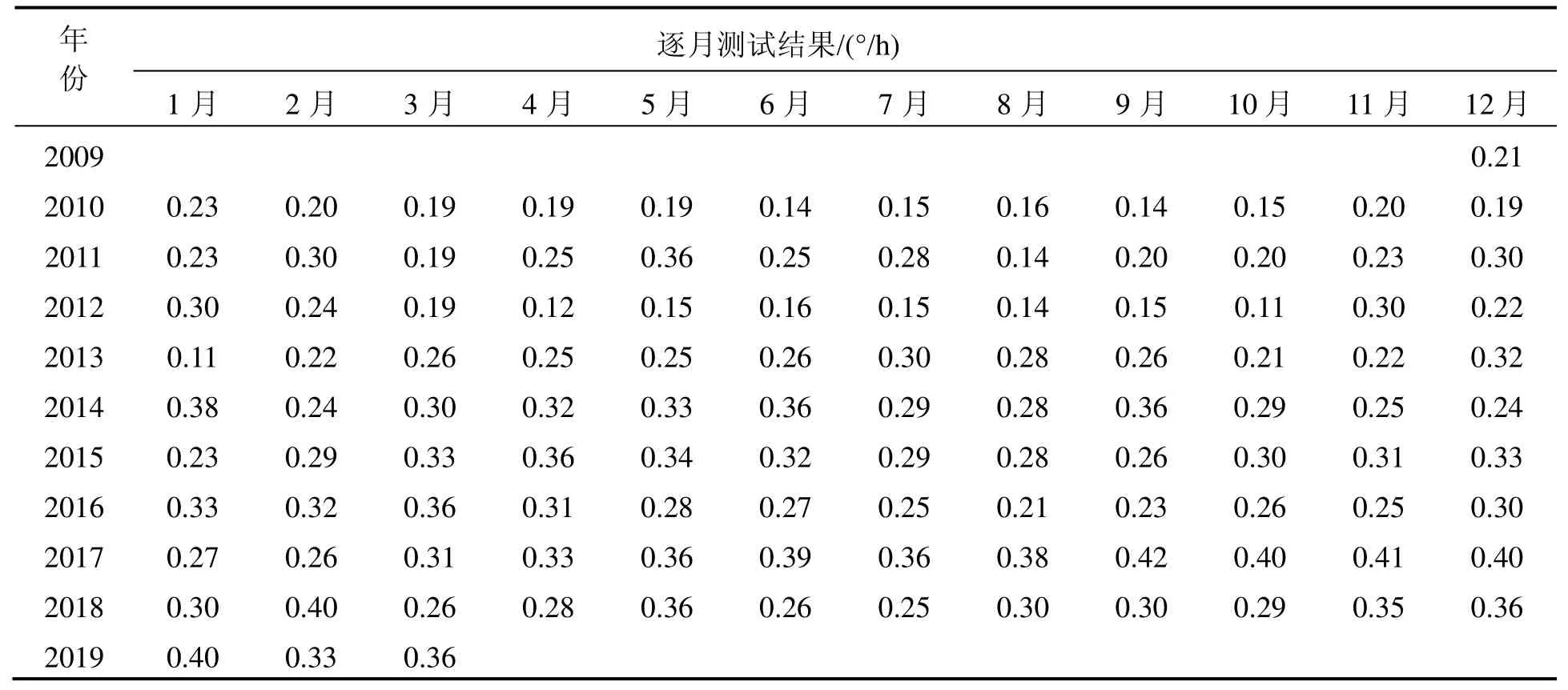
表1 陀螺零位测试数据表Tab.1 FOG bias data

3.2 参数计算

通过3.1节分析，将正倒向随机微分方程组的参数估计问题转换为一个随机微分方程的参数估计问题，进而根据最大似然估计方法，得出参数的一致性估计。参数估计问题转化为对如式(20)所示方程求根：

对式(20)展开可得：

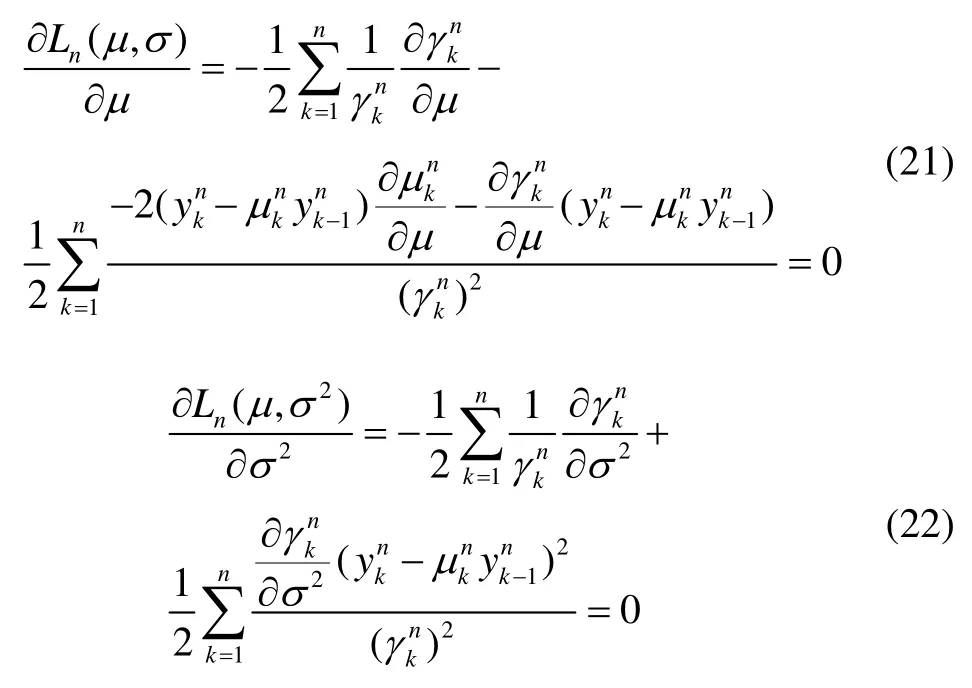
利用 Matlab的求根数值解算方法，将表1中的2009～2014年陀螺逐月零位测试数据代入方程中，获得最优的参数估计值为= 0.6532 ，=0.9755。

将参数值代入方程式(10)中，就得到了光纤陀螺零位输出变量tY的线性随机微分方程。为了验证模型的适宜性和参数的稳定性，利用已知方程可求得模型的计算值，即光纤陀螺零位的估计值。将估计值与实际测量值相对比，可对模型的适宜性进行分析判断。

模型和参数值验证估计效果如图1所示。图中蓝色点表示陀螺零位的实际测量值，红色点表示利用方程推导出的陀螺零位估计值。经计算拟合误差的均方根值为0.0481 (°)/h。从验证的效果看，其拟合优度可决系数R2=0.7033，拟合度较好，在一定程度上可以用式(10)的方程模型来刻画陀螺零位的变化。

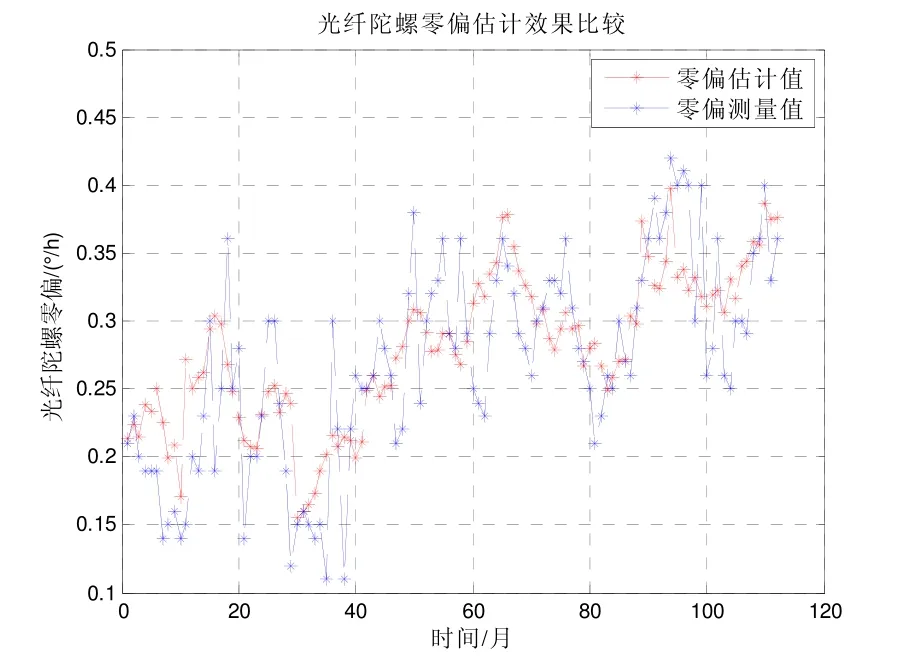
图1 模型估计值和同实测值对比图Fig.1 Comparison of model estimates and measured value

3.3 应用示例

利用式(10)得到的光纤陀螺正倒向随机微分方程模型，可用于求解在给定将来时刻目标值的情况下，如何得到当前（产品出厂）时刻的允许值。

以实际应用为例，用户要求光纤陀螺在卫星上连续工作 10 年后的零偏不大于 4.0 (°)/h（即ω=4.0 (°)/h），为了确保陀螺满足卫星寿命要求，需确定在出厂时刻（即T=0）允许的零位数值最大值。

求解光纤陀螺倒向随机微分方程，可获得所需结果。由于倒向随机微分方程含有随机过程，相关解法不如常规微分方程的解法成熟，为此相关学者对倒向微分方程的数值解法进行了大量研究[9]，主要从纯数学角度研究如何提高算法精度，其中涉及到大量的数学条件期望求解算法等。

本文重点关注模型的建立和工程应用，数值精度不是重点，因此利用最基本的欧拉数值解法，通过对布朗运动进行蒙特卡罗方法模拟，将参数（,）代入进行求解。

蒙特卡罗方法对随机过程的布朗运动抽样生成的一般方法为：

● 采样点 0 =t0＜t1＜t2＜…＜tn；

● 标准正态分布 (0,1)N抽样产生

k= 1 ,2,… ,n。

经过对微分方程的欧拉数值解法计算，在陀螺10年后的零位不大于4.0 (°)/h（即ω=4.0 (°)/h）情况下，陀螺出厂零位应不大于1.5 (°)/h。计算获得的陀螺连续工作10年（120个月）的零位变化如图2所示。

图2 估计的陀螺零位变化图Fig2 Variation curve of FOG estimate bias

为了清楚得到陀螺的零位变化趋势，在数据处理上进行了平滑处理。结果可以看出，在终端时刻的要求不同，初始时刻的取值不同。

4 结论和展望

本文从光纤陀螺零位随机漂移的规律和模型出发，建立光纤陀螺的倒向随机微分方程模型，并利用最大似然估计法求解了模型参数，并对模型和参数进行了分析和验证，最后以某光纤陀螺产品实际要求为例，获得了满足用户零位稳定性要求的出厂控制指标。

由于倒向随机微分方程在工程领域的实际应用尚处于探索阶段，本文也是首次将倒向随机微分方程应用于光纤陀螺的质量控制领域，研究子样还不够多，后续还需要对模型的适应性进一步进行验证，但该方法对拓展光纤陀螺乃至惯性产品质量管控的研究视野必将起到积极的作用。