不同尺寸钢球在42CrMo钢平板上许用接触应力研究

杨 哲

(1.洛阳LYC轴承有限公司，河南 洛阳 471039； 2.航空精密轴承国家重点实验室，河南 洛阳 471039)

滚动轴承的滚动面在大载荷的作用下，滚动面将会产生永久变形，该变形的变形量随着载荷的变大而增大。根据GB/T 4662标准，永久变形量等于0.0001时，用此变形量的当量静载荷作为轴承的额定静载荷[1]。特大型转盘轴承所受的载荷主要为静载荷，转速低，与平板钢球接触类似，因此通过平板压力试验，用线性回归法计算出永久变形量和最大接触应力之间的线性关系，然后计算出许用接触应力[2-6]。研究42CrMo钢的许用接触应力对轴承的设计，可靠性分析有重要的意义。国内很多专家在42CrMo钢对滚子的许用接触应力上面做了很多研究，并取得了一定的成果，但是42CrMo钢对钢球的许用接触应力却没有见到相关的报道。本项目通过研究表面硬度为58～61 HRC的不同尺寸钢球，在表面硬度为57～60 HRC和淬硬层深度为5 mm的平板上的平板压力试验，研究淬硬层深度对许用接触应力的影响。

1 试验设备和方法

1.1 试验设备

液压万能材料试验机，如图1所示。SH65淬硬层测深仪，CL-1A轮廓仪，如图2所示。

1.2 试验方法

试验方法如下：

图2 轮廓仪Fig.2 Contourgraph

(1)试验材料选取42CrMo钢锻造后，加工成平板试样，经过预处理，不同工艺的中频表面淬火，得到表面硬度为57～60 HRC、硬化层深度为5 mm的试样。其中淬硬层深度用SH65淬硬层测深仪检测。

(2)将上述材料切割成80 mm×50 mm×35 mm的平板试样，将其分为ⅰ、ⅱ、ⅲ三组，每九个试样为一组，其中每组试样备用两个。

(3)用φ38 mm的钢球，通过WE-600型液压万能材料试验机分别对ⅰ组9个试样施加25、30、35、40、50、60、70、80、90 kN的垂直于平板表面的载荷，载荷保持3 s，由于加载载荷时有冲高，计算过程按实际载荷计算，试样ⅱ、ⅲ的试验方法同试样ⅰ，试验力如表1所示。

(4)压痕深度用CL-1A轮廓仪检测。

2 结果与分析

2.1 压痕深度测量

压痕深度用轮廓仪测量，三组试样压痕深度如表1所示。

2.2 许用接触应力的计算

根据赫兹理论[1-6]，应力和载荷的关系如公式1所示。

表1 三组试样在不同载荷下的压痕深度

Table 1 The indentation depth of three sets of specimens under different loads

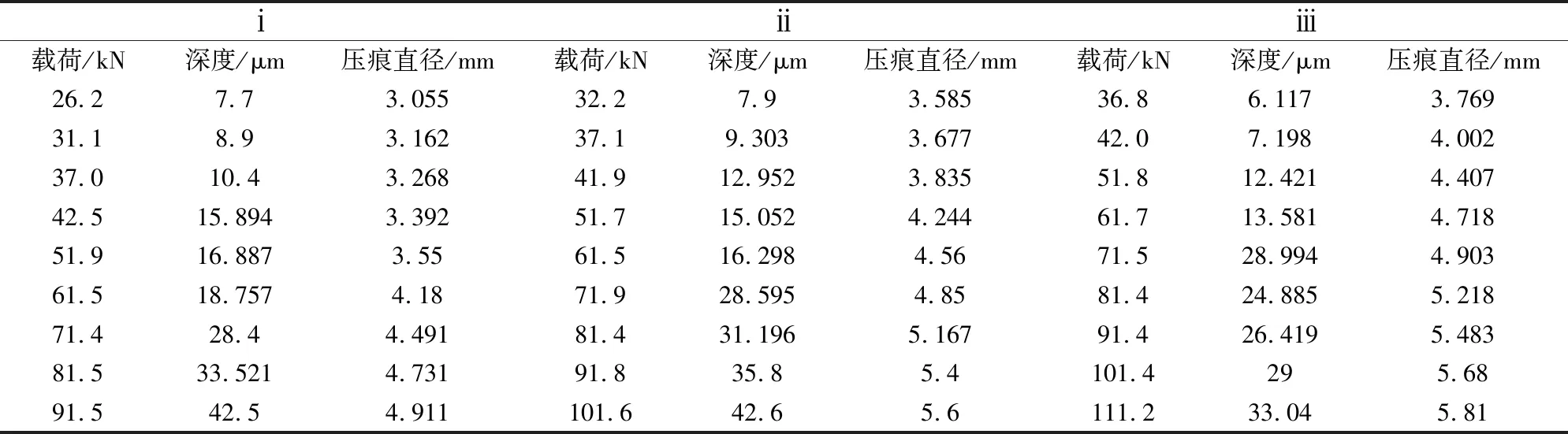
ⅰⅱⅲ载荷/kN深度/μm压痕直径/mm载荷/kN深度/μm压痕直径/mm载荷/kN深度/μm压痕直径/mm26.27.73.05532.27.93.58536.86.1173.76931.18.93.16237.19.3033.67742.07.1984.00237.010.43.26841.912.9523.83551.812.4214.40742.515.8943.39251.715.0524.24461.713.5814.71851.916.8873.5561.516.2984.5671.528.9944.90361.518.7574.1871.928.5954.8581.424.8855.21871.428.44.49181.431.1965.16791.426.4195.48381.533.5214.73191.835.85.4101.4295.6891.542.54.911101.642.65.6111.233.045.81

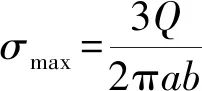
(1)

式中：σmax为最大接触应力，MPa；Q为载荷，N；a、b分别为压痕的长短经，mm。

根据公式1计算出应力的结果如表2所示。

然后根据应力和压坑深度求出永久变形δq/Dw和最大接触应力σmax之间的关系，即

δq/Dw=Kσmaxb

(2)

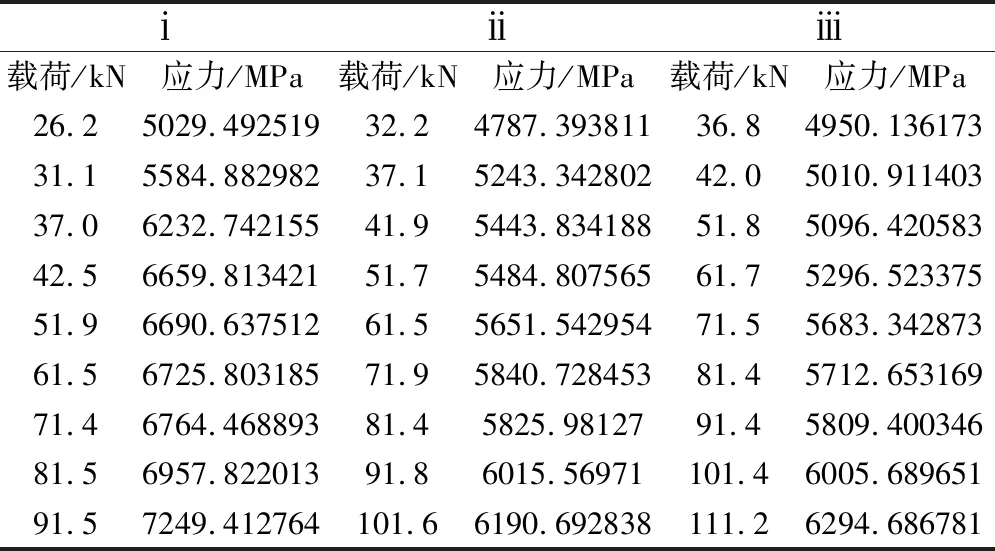
表2 三组试样在不同载荷下的应力

式中：δq/Dw表示永久变形量，即滚子压痕深度与钢球直径之比；σmax为最大接触应力，MPa；b为指数；K为常数。式(2)为经验公式。

对式(2)两边取对数，得

lg(δq/Dw)=b(lgσmax)+lgK

(3)

令y=lg(δq/Dw)，x=lgσmax，a=lg K，则式(3)能变换为y与x的线性关系，

y=a+bx

(4)

根据表1和表2计算出来ⅰ、ⅱ、ⅲ三组试样各个载荷下的lg(δq/Dw)和lgσmax如表3所示。

使用origin软件对表3中ⅰ组数据线性回归，可得以下结果。

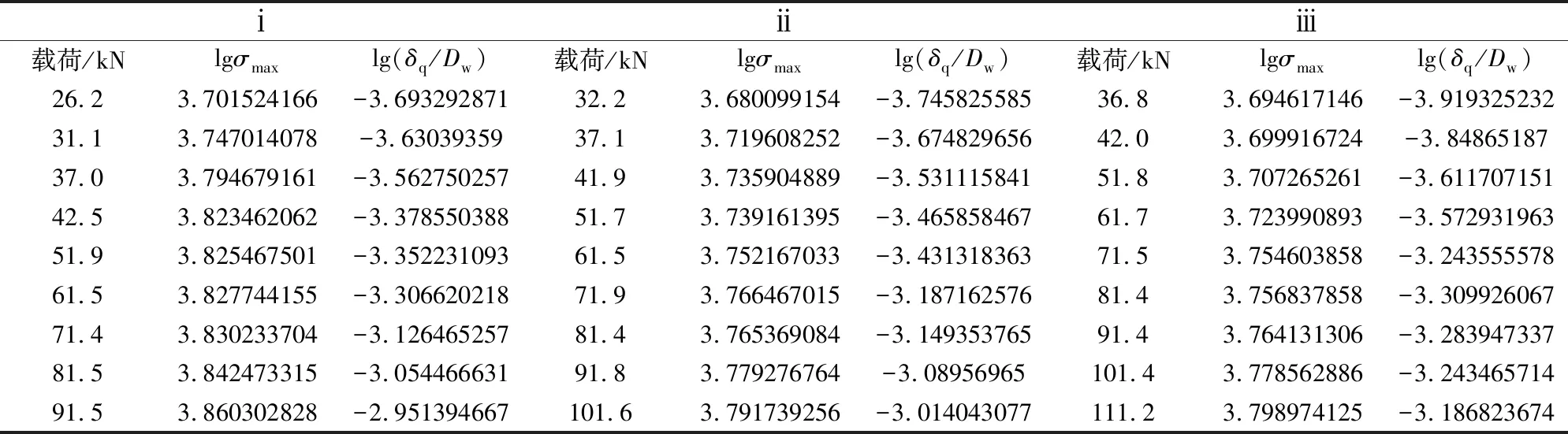
表3 应力和永久变形量的对数值

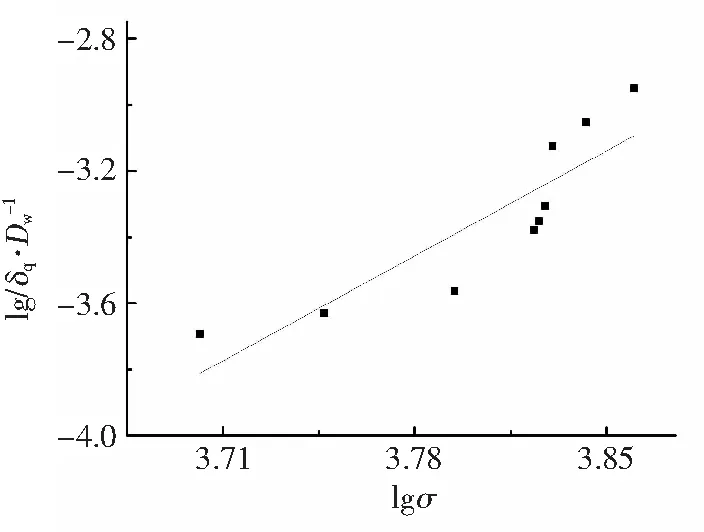
图3 ⅰ组试样的线性拟合曲线Fig.3 linear fitting curve of ⅰ group specimen

得出一次线性拟合曲线如下：

y=4.531x-20.585

(5)

相关系数r=0.910，r>0.9，∴lgσ和lg(δq/Dw)正相关，即x和y正相关。

由式(5)得：

lg(δq/Dw)=4.531lgσ-20.585

(6)

δq/Dw=σ4.531×10-20.585

(7)

σ=(δq/Dw×10-20.585)1/4.531

(8)

根据许用接触应力定义，永久变形量δq/Dw=10-4时，根据式(8)求出的σ值即为许用接触应力。当δq/Dw=10-4时，许用接触应力σ1=4574.460 MPa。

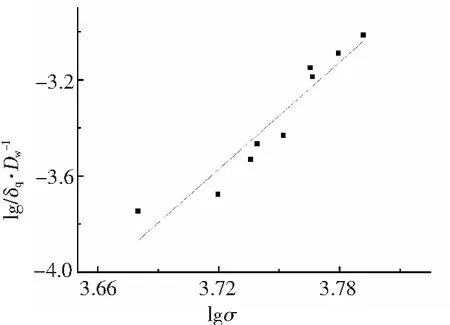
图4 ⅱ组试样的线性拟合曲线Fig.4 Linear fitting curve of ⅱ group specimen

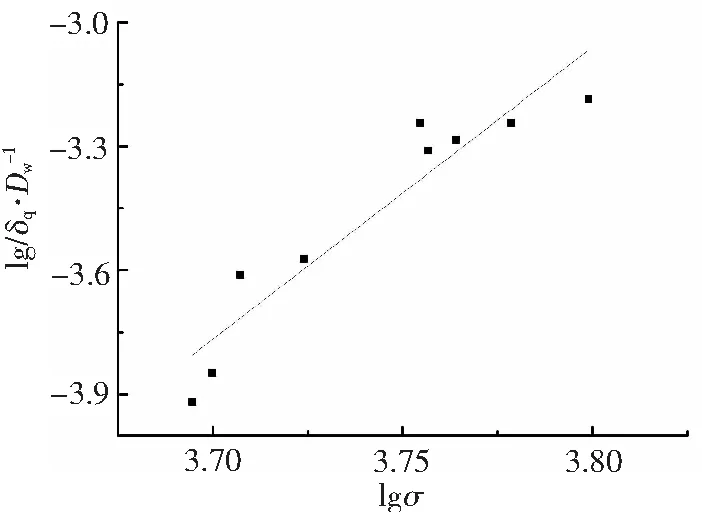
图5 ⅲ组试样的线性拟合曲线Fig.5 Linear fitting curve of ⅲ group specimen

对表3中ⅱ组数据进行线性回归，得出一次拟合曲线如下：

y=7.428x-31.204

(9)

相关系数r=0.901，r>0.9，∴lgσ和lg(δq/Dw)正相关，即x和y正相关。当δq/Dw=10-4时，ⅱ组试样计算出的许用接触应力σ2=4595.773 MPa。

对表3中ⅲ组数据进行线性回归，得出一次拟合曲线如下：

y=7.07x-29.926

(11)

相关系数r=0.912，r>0.9，∴lgσ和lg(δq/Dw)正相关，即x和y正相关。当δq/Dw=10-4时，ⅲ组试样计算出的许用接触应力σ3=4645.622 MPa。

2.3 计算结果分析

根据以上计算结果，不同尺寸的钢球在淬硬层深为5 mm，硬度为57～60 HRC的42CrMo平板上的许用接触应力随着钢球尺寸的增加而增大。这主要是因为钢球的尺寸越大，弧度越大，压载的变形过程中，接触面积就越大，抵抗变形的能力也就越强，也就表现为许用接触应力越大。

3 结论

1)根据线性回归的结果，lg(δq/Dw)和lgσmax存在线性回归关系。

2)根据计算得出表面硬度58～61 HRC的尺寸φ38、φ44、φ50.8 mm的钢球在硬度为57～60 HRC和淬硬层深度为5 mm的平板上许用接触应力分别为4574.460、4595.773、4645.662 MPa。

3)当平板的表面硬度为57～60 HRC，淬硬层深度为5 mm时，随着钢球尺寸的增加，许用接触应力增大。