基于二维位移传感器的砂轮表面形貌测量*

张 霞, 蔡顺燕, 李红梅, 林 梅

(成都师范学院 物理与工程技术学院, 成都 611130)

磨削是利用砂轮中的磨粒进行微量切削加工的过程，砂轮表面的三维形貌对磨削力、材料去除方式、磨削温度和工件表面质量等有重要影响[1-2]。准确有效地测量和分析砂轮表面的三维形貌，是提高磨削工件表面质量、优化砂轮修整工艺参数和磨削加工工艺参数的重要依据。特别是一些特殊工件材料的加工，方便、准确地测量加工时砂轮的表面三维形貌参数，将对整个磨削加工过程有重要指导作用[3-4]。

目前，很多国内外学者对此进行了大量研究。霍凤伟等[5-6]使用基于白光干涉原理的三维表面轮廓仪精确测量砂轮的表面形貌，取得了较好效果；XIE等[7-8]利用扫描电子显微镜对比了不同砂轮的表面形貌；CAI等[9-11]利用激光共聚焦三维测量仪对砂轮表面形貌进行测量，并计算了其表面形貌参数。

常用测量方法的测量过程往往复杂耗时，还需要将砂轮从机床上拆卸后测量，无法实现砂轮的在线测量。如何方便准确地在线测量机床砂轮的表面三维形貌参数并对其评价，是目前急需解决的磨削问题。

随着现代超精密测量仪器的发展，采用二维(2D)位移传感器可实现机床砂轮表面形貌的在线测量。测量中砂轮以一定速度旋转，设置二维位移传感器的采样频率来获得砂轮表面的三维(3D)形貌数据[12]。李厦等[12-13]采用激光位移传感器测量氧化铝砂轮的三维形貌，获取了砂轮局部表面形貌模型，评价了多粒度号氧化铝砂轮的磨粒密度、出刃高度、有效出刃高度等特性参数；但该方法计算过程复杂，需要拟合砂轮出刃高度曲线，其结果的准确性对实验环境的依赖性较高，难以在实际生产中应用。

为此，提出一种简单有效分析砂轮表面三维形貌的方法。通过对砂轮表面三维形貌的基准平面进行计算和数字滤波后，获得砂轮表面三维形貌的评价参数，可对砂轮形貌特征进行描述，最后通过实验验证该方法的有效性。

1 砂轮表面形貌评价方法

1.1 砂轮表面形貌的基准平面

砂轮三维形貌的显示和评定需要有一个基准面。实际被测砂轮表面不能作为基准面，而砂轮的设计表面是理想表面，在实际使用后其位置变化，也不能作为基准面。我们用最小二乘法来确定被测砂轮的基准平面。图1为砂轮表面形貌测量示意图。

如图1所示：设x正方向为沿砂轮轴线向左方向，y正方向为砂轮表面圆周切线旋转方向，在x和y方向上的采样数据点间隔Δx和Δy分别为：

(1)

将2D激光位移传感器测量的(xi,yj)坐标处的实际高度值定义为f(xi,yj)(xi=iΔx,yj=jΔy;i=1,2,...,M;j=1,2,...,N)

式中：Ls为x方向采样数据点总长度，υs表示砂轮转速，fk表示采样频率，M和N分别表示在x和y方向的总采样点数。

设最小二乘法的基准平面函数：

z(x,y)=ax+by+c

(2)

式中：a,b,c分别为实数系数。

设ξ(xi,yj)表示残差表面函数，是原始数据与基准平面之间的差异，如式(3)所示：

ξ(xi,yj)=f(xi,yj)-z(xi,yj)

=f(xi,yj)-(axi+byj+c)

(3)

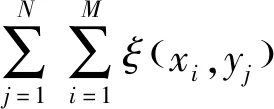
(4)

(5)

求解式(5)，可求出a，b，c的值；然后代入式(3)和式(4)，可得到最小二乘法的基准平面函数z(x,y)和残差表面数据ξ(xi,yj)。残差表面数据ξ(xi,yj)将用作滤波和计算三维形貌参数的数据源。

1.2 数字滤波

由于实验测量的砂轮三维形貌数据含有系统干扰和砂轮表面的高频成分，不能直接用于砂轮表面三维形貌的分析及评价，故采用频谱分析和数字滤波方法对测得的原始数据进行预处理[13]。在欧式坐标系中，残差ξ(xi,yj)的M×N数字阵列为ξ(xi,yj)，其中xi=iΔx,yj=jΔy;i=1,2,…,M;j=1,2,…,N。

对其进行三维离散傅里叶变换，得到：

(6)

式中：p=0,1,…,M-1；q=0,1,…,N-1。

沿x,y方向的空间频率up,vq如式(7)所示：

(7)

式中：p和q分别表示x和y方向的采样点数。

为了去除高频正弦分量，我们采用理想的低通滤波传递函数：

(8)

式中：ω1为低通滤波的截止频率。

滤波系统的频域输出，如式(9)所示：

G(up,vq)=H1p(up,vq)·F(up,vq)

(9)

然后用傅里叶逆变换来重建砂轮表面的三维形貌数据，如式(10)所示：

(10)

式中fh(xi,yj)(xi=iΔx,yj=jΔy;i=1,2,…,M;j=1,2,…,N)是滤波后的表面残差数据，将被用于砂轮表面三维形貌参数的计算。

1.3 砂轮表面形貌评价参数

砂轮表面的三维形貌参数是对砂轮表面的微观几何形状特性的某些方面做出的精确描述，可有效反映出机床砂轮表面的微观几何形状、不平度高度、宽度、砂轮磨损及摩擦润滑等特性[3-4]。

1.3.1 与微观不平度高度有关的参数

(1)表面形貌的算术平均高度ha：

(11)

(2)表面形貌的高度均方根偏差hq：

(12)

式(11)和(12)的ha和hq是对整个表面形貌高度信息的描述，是简单常用的高度参数。

(3)表面形貌的最大峰值hp：

hp=max(fh(xi,yj))

(13)

即hp是测量区域内最高峰相对于基准平面的高度。

(4)表面形貌的最大谷值hv：

hv=min(fh(xi,yj))

(14)

即hv是测量区域内最低谷相对于基准平面的高度。

(5)表面形貌的最大高度值hz：

hz=hp-hv

(15)

即hz是测量区域内最高峰值和最低谷值的高度差。

式(13)、式(14)和式(15)中：hp可有效反映砂轮表面磨粒的切削特性；hv反映砂轮表面容纳冷却液的体积；hz是砂轮形貌起伏的最大高度，当砂轮发生机制磨损时，hz可快速表达出高度的变化。

1.3.2 与微观不平度间距有关的参数

(1)表面形貌的均方根斜率dΔq：

(16)

(2)表面形貌的展开界面面积比Sdr：

界面元素为实际表面上点(xi,yj)处的最小采样四边形。界面元素的面积Aij为:

(17)

界面面积比Sdr如式(18)所示：

(18)

式(16)和式(18)中dΔq和Sdr值越大，说明表面形貌高度、宽度或两者都显著，与砂轮堵塞磨损有一定关系。

1.3.3 与微观不平度形状有关的参数

(1)表面高度分布的偏斜度Fsk：

(19)

(2)表面高度分布的峭度Fku

(20)

根据参考文献[5]可知：式(19)中Fsk为负值时表面呈饱满形，相应耐磨性好；为正值时表面呈空虚形。故Fsk能表达不同的表面磨损条件类型。式(20)中Fku是与正态分布形状为标准来比较的参数，当峭度分布符合正态分布时Fku=3，大于3时表示峭度分布较陡，小于3时表示较为平坦。

2 砂轮表面形貌的实验研究

2.1 砂轮表面形貌测量条件及过程

图2为砂轮表面形貌测量实验实物图。图2中：实验机床为德国Schleifring公司K-P48T平面磨床；磨削砂轮为单晶刚玉(SA)砂轮:型号WA60H10V，直径330 mm；选用KEYENCE公司的超高精度2D激光位移传感器，型号LJ-G015，波长650 nm，量程5.2 mm，分辨率0.2 μm。

测量时，首先将超高精度2D激光位移传感器的测头安置于被测机床砂轮表面的正下方，再调整其激光射线，使其垂直于被测砂轮表面。设定传感器信号采样频率fk=250 Hz，传感器每次采样的数据点数为800。实际测量过程中，先启动机床砂轮作低速转动，通常设置砂轮转速υs≤1 m/s，再触发2D激光位移传感器进行数据采集，同时将传感器采集的数据信号通过控制器传送到计算机进行分析处理。

2.2 测量实验结果

在砂轮转速分别为0.2 m/s和0.5 m/s 的条件下测量砂轮表面形貌，经1.1中的砂轮表面基准平面及1.2中的数字滤波计算后，用Matlab软件处理实验数据，获得砂轮表面的三维形貌如图3。

利用1.3中的砂轮表面形貌参数计算公式得出图3的三维形貌参数评价如表1所示。从表1可以看出：在不同砂轮转速下2组对应的各参数基本相同，不受砂轮转速变化的影响；且表1的评价参数较为全面地描述了砂轮的表面形貌特征，为保证砂轮修整效果及工件磨削质量提供了基本指标和依据。

2.3 实验验证

为验证上述二维位移传感器测量评价方法的有效性和实用性，利用美国Zeta自动三维测量系统对砂轮表面进行测量，并将该仪器的测量结果与二维激光位移传感器的测量计算结果对比，结果如表2。Zeta三维测量系统及实测砂轮表面形貌过程如图4。

表1 砂轮表面三维形貌评价参数表

表2 测量结果对比表

(a)Zeta自动三维测量系统Zetaautomaticthree-dimensionalmeasurementsystem(b)Zeta测量砂轮表面形貌过程Zetameasurementofsurfacemorphologyofgrindingwheel图4 Zeta三维测量系统及实测砂轮表面形貌过程Fig.4Zetathree-dimensionalmeasuringsystemandtheprocessofmeasuringgrindingwheelsurfacetopography

表2中2种方法的测量结果基本相同，验证了本文使用的2D激光位移传感器测量计算砂轮表面形貌方法的可行性和实用性，对砂轮表面三维形貌测量的后续研究及评价有指导意义。

3 结论

(1)提出了磨削加工过程中基于二维激光位移传感器的砂轮表面形貌测量及评价方法，实现其在线测量及评价。

(2)根据二维激光位移传感器的测量原理，建立三维形貌基准平面和数字信号滤波方法，通过测量数据来计算砂轮表面的三维形貌参数。

(3)用二维激光位移传感器实验测量砂轮表面，比较不同砂轮转速下砂轮表面的形貌参数，并与Zeta自动三维测量系统的测量结果进行对比，验证了该方法的有效性和实用性；该方法使用简单，测量时不用拆卸砂轮，具有良好的应用前景。