一种弹性支撑双稳态压电能量俘获系统的动力学仿真分析

王康　李欣业　张利娟　张华彪

摘要：為了揭示双稳态能量俘获系统的复杂动力学行为及现象，针对弹性支撑下具有双稳态的压电悬臂梁能量俘获系统的动力学行为进行研究。首先基于能引发双稳态现象的磁力模型，利用牛顿第二定律以及基尔霍夫第一定律建立了基础作简谐运动时系统的数学模型。其次根据无量纲化后的控制方程，利用罗斯-霍尔维茨判据分析了平衡点的静态分岔。最后，利用Matlab数值仿真得出压电悬臂梁位移以及输出电压随系统参数和激励参数的变化规律和分岔图。结果表明，系统的幅频特性呈现为硬特性，但压电悬臂梁的振幅随质量比及刚度比的变化却呈软特性，即在某些参数范围内，系统的简谐周期响应发生分岔并导致混沌运动，系统的运动既可以发生在零平衡点附近，也可以发生在非零平衡点附近，甚至是在不同的平衡点之间作大幅跃迁。因此，相同参数下，系统具有双稳态时比单稳态时具有更丰富的运动形式，可明显提高系统的电压输出和响应频带。研究结果可为工程实际中如何优化振动能量采集器提供理论依据。

关键词：非线性动力学;双稳态压电能量俘获系统;弹性支撑;分岔分析;数值仿真

中图分类号：O322;TH123+.1文献标志码：A

WANG Kang，LI Xinye，ZHANG Lijuan，et al.Dynamical simulations of a bi-stable piezoelectric energy harvesting system with elastic support[J].Journal of Hebei University of Science and Technology，2019，40（3）：242-251.Dynamical simulations of a bi-stable piezoelectric energy

harvesting system with elastic support

WANG Kang1， LI Xinye1， ZHANG Lijuan1， ZHANG Huabiao2

（1.School of Mechanical Engineering， Hebei University of Technology， Tianjin 300130， China; 2. Institute of Mechanical Engineering， Tianjin University of Commerce， Tianjin 300134， China）

Abstract：The dynamic behavior of a piezoelectric cantilever energy harvesting system with bi-stable state under elastic support is studied to reveal its complex phenomena. Based on the magnetic force model which can induce bi-stable phenomena， the mathematical model of the system with two degree of freedom under harmonic base motion is firstly established by using Newton's second law and Kirchhoff′s law. By the Routh-Hurwitz criterion， the static bifurcation of equilibrium points， is secondly analyzed for the dimensionless governing equations. At last， the amplitude variations of the displacement of piezoelectric cantilever beam and the variations of the output voltage with the system parameters and excitation parameters and their bifurcation diagrams are obtained by Matlab numerical simulations. The results show that the amplitude-frequency curves of the system are in hard characteristic， while the amplitude variations of the displacement of piezoelectric cantilever beam with mass ratio and stiffness ratio are in soft characteristic. That is， within some parameters intervals， the harmonic response of the system has bifurcation and leads to chaotic motion. The motion of the system can take place near the zero or non-zero equilibrium point， even jump with large amplitude between the two non-zero equilibrium points. For the same parameters， bi-stable systems have richer forms of motion compared to mono-stable ones， and significantly increase voltage output and response frequency band of the system. The research result may provide theoretical reference for how to optimize vibration energy collector in practice.

Keywords：nonlinear mechanics; piezoelectric energy harvesting systems with bi-stable state; elastic support; bifurcation analysis; numerical simulation

无线传感器、移动电子设备等的发展对能源的供应方式提出了更高的要求[1]，因为传统的电池供电方式存在诸多不足：一是电池的容量有限，必须进行定期更换，而且污染环境;二是在高温、强腐蚀等恶劣环境下电池难以长期使用;三是电池体积较大，严重限制了无线传感器节点的微型化和集成化。为了解决这些低功耗电子设备的持久可靠供电问题，能量俘获正成为学术界和工业界共同关注的一个前沿技术领域[2]。

振动能在自然界中是普遍存在的，且不像太阳能、电磁能那样受到使用时间、服役环境等因素的限制，因此针对振动能量俘获的研究目前最为广泛。为了提高振动能量俘获系统的能量转换效率，研究者们提出了一系列方法：在线性系统的基础上通过增加非线性来提高能量俘获效率[3-5];通过引入非线性磁力模型使系统具有双稳态来提高能量俘获系统的响应频带[6-11];在双稳态的基础上通过增加磁铁块的方法使系统具有三稳态，使得系统在低激励频率和低激励幅值下均能发生大幅运动[12-15];改变能量俘获系统的结构，比如将刚性支撑改为弹性支撑、采用具有高柔性的压电材料等来提高压电悬臂梁的变形程度，进而提高能量俘获效率[16-17];把单自由度系统扩展到多自由度系统，通过不同模态之间的相互作用来提高系统的响应特性[18-21];或通过改善能量俘获系统的外接电路来提高能量的收集效率[22]。

河北科技大学学报2019年第3期王康，等：一种弹性支撑双稳态压电能量俘获系统的动力学仿真分析本文基于能引发双稳态的磁力模型，针对一种具有弹性支撑的压电悬臂梁能量俘获系统的动力学行为展开研究，第1部分利用牛顿第二定律以及基尔霍夫第一定律建立了能量俘获系统的动力学方程，第2部分对系统平衡点做了静态分岔分析，得出了平衡点的个数及其稳定性的变化，第3部分采用数值求解的方法研究了压电悬臂梁的输出电压随系统参数和激励参数的变化规律，最后是本文的主要结论。

1数学模型

本文分析的双稳态振动能量俘获系统的基本结构及其等效集总参数模型如图1所示， 其是由压电悬臂梁、永磁铁及弹性支撑组成，其中压电悬臂梁AB是由金属板和压电陶瓷片（PZT）组成的。当基础振动时，压电悬臂梁AB会随之产生振动，进而使得PZT产生变形，根据压电效应就可以实现振动能到电能的转化。若将压电悬臂梁AB和弹性支撑等效为弹簧阻尼系统，则可以得到如图1 b）所示的等效集总参数模型。其中，Keq，Meq和Ceq分别表示压电悬臂梁的等效刚度、末端等效质量和等效阻尼;Kb，Mb和Cb分别表示弹性支撑的等效刚度、等效质量和等效阻尼;Cp和α表示压电陶瓷的夹持电容和机电转换系数，V为能量俘获系统的输出电压，x为压电悬臂梁的振动位移，y为弹性支撑的振动位移，z=A sin（ωt）=A sin（2πft）为基础运动，其中f为外激励频率。

根据牛顿第二定律可以得到该系统的运动微分方程Meq+Ceq（-）+Keq（x-y）+αV-Fv=0，Mb+Cb（-）+Kb（y-z）+Ceq（-）+Keq（y-x）+Fv=0，（1）其中Fv为磁铁间的磁力沿着竖直方向的分力，将其表达式Fv=Fxx2+d2在x=0处进行泰勒展开并保留前两项可得Fv=Fdx-F2d3x3，（2）其中，F为两磁铁间的磁力，d为两磁铁间的间距。将式（2）代入式（1）可得Meq+Ceq（-）+Keq（x-y）+αV-Fdx+F2d3x3=0，Mb+Cb（-）+Kb（y-z）+Ceq（-）+Keq（y-x）+Fdx-F2d3x3=0。（3）根据基尔霍夫第一定律可以得到系统的电路方程α（-）=Cp+VR。（4）式（3）与式（4）即为系统的控制方程，引入无量纲变换=x/l，=y/l，=t/T，ν=V/e，其中l为压电悬臂梁的长度，T=Meq/Keq，e=Meqg/α。为方便，变换后的，仍记为x，y，则无量纲化后控制方程的形式为

+2ξ+βx+γx3-2ξ-y+ψν=0，+2ξc+1a+b+1ay-2ξa-βax-γax3=h sin（Ωt+φ），+μν+θ-θ=0。（5）

其中a=MbMeq，b=KbKeq，c=CbCeq，ξ=Ceq2Meq，β=1-FdKeq，γ=Fl22Keqd3，ψ=MeqgKeql，

μ=1RCp，θ=αlCpe，Ω=ω，h1=bAαl，h2=cAΩCeqaKeql，h=h21+h22，tan φ=h2h1。

2平衡點静态分岔分析

通过系统的结构模型可以发现，当基础不受外激励作用时，通过受力分析可知，由于引入了磁力模型，系统除了悬臂梁处于水平位置时受力平衡外，在上、下也各有一个受力平衡位置。下面通过分析方程（5）对应的自治系统的平衡点及其稳定性，来说明此系统的静态分岔特性。令x1=x，x2=，x3=y，x4=，x5=ν，则方程（5）对应的自治系统可以写成=f（x）这种矩阵形式。

令f（x）=0，通过分析可知，当β≥0时，系统只有1个平衡点（0，0，0，0，0）;当β<0时，系统有3个平衡点，分别为（0，0，0，0，0），（±-β/γ，0，0，0，0）。下面将分别讨论它们的稳定性。

当β≥0时，对应唯一平衡点（0，0，0，0，0），其雅克比矩阵对应的特征方程为λ5+[2ξa（1+a+c）+μ]λ4+[2ξa（μ+aμ+cμ+2cξ）+b+1a+θψ+β]λ3+

[2ξa（b+cβ+cθψ+2cξμ）+b+1aμ+βμ]λ2+[2ξa（bμ+cβμ）+b+1aθψ+βa（b-θψ）]λ+bβμa=0。（6）当β>0时，由于a，b，c，ξ，ψ，μ，θ为正，根据罗斯-霍尔维茨判据可知，平衡点（0，0，0，0，0）是渐近稳定的。

当β=0时，特征方程变为λ5+[2ξa（1+a+c）+μ]λ4+[2ξa（μ+aμ+cμ+2cξ）+b+1a+θψ]λ3+

[2ξa（b+cαψ+2cξμ）+b+1aμ]λ2+[2ξbμa+b+1aθψ]λ=0。（7）此时该特征方程具有零根，对应的平衡点（0，0，0，0，0）为分岔点。

当β<0时，对于平衡点（0，0，0，0，0），根据罗斯-霍尔维茨判据，由式（6）可知，其特征多项式必有正实部根，故平衡点（0，0，0，0，0）是不稳定的。对于平衡点（±-β/γ，0，0，0，0），其雅克比矩阵对应的特征方程为λ5+[2ξa（1+a+c）+μ]λ4+[2ξa（μ+aμ+cμ+2cξ）+b+1a+θψ-2β]λ3+[2ξa（b-2cβ+cθψ+

2cξμ）+b+1aμ+2βμ]λ2+[2ξa（bμ-2cβμ）+b+1aθψ-2βa（b-θψ）]λ-2bβμa=0。（8）根据罗斯-霍尔维茨判据可得，平衡点（±-β/γ，0，0，0，0）是渐近稳定的。

通过上述分析可知，当β>0时系统有一个稳定的零平衡点，当β<0时系统有2个稳定的非零平衡点和一个不稳定的零平衡点，故β=0时为叉形分岔点。

3数值仿真

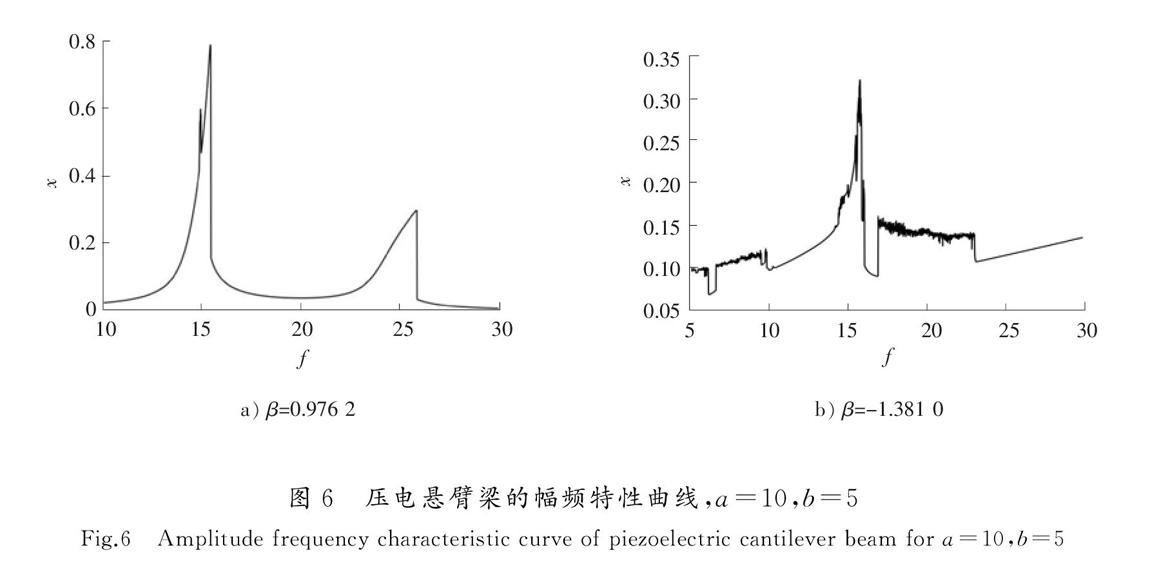
本部分利用龙格-库塔方法对无量纲化后的控制方程（5）进行数值求解时分别考虑了系统具有单稳态（β=0.976 2）和双稳态（β=-1.381 0）两种情况，分别分析系统参数和外激励参数等对系统悬臂梁位移以及电压响应特性的影响，结果如图2—图7所示，求解中涉及到系统参数如表1所示。其中，图2—图5为系统的质量比和刚度比对系统悬臂梁位移以及电压响应特性的影响，图6和图7为外激励频率对系统悬臂梁位移以及电压响应特性的影响。对比图2、图4以及图6 a）和图6 b）可以发现，相同参数下，当系统具有双稳态时，虽然压电悬臂梁位移的最大值没有单稳态时大，但是在更大的参数范围内，具有双稳态时系统压电悬臂梁的位移比具有单稳态时要大;对比图3、图5以及图7 a）和图7 b）可以发现，相同参数下，当系统具有双稳态时系统输出电压值比单稳态时高;图6和图7分别表示外激励频率对压电悬臂梁位移以及输出电压的影响，从图中可以看出，当系统具有单稳态时，系统只在2个共振频率附近才有较高的位移响应和电压输出，但是当系统具有双稳态时，系统除了在2个共振频率附近有较高的位移响应和电压输出外，在较大的频带范围内系统仍具有比较大的位移响应和电压输出，特别是系统受到频率较低的外激励时，仍然可以有效地采集能量，即双稳态的引入可以有效拓宽系统的响应频带。通过分析质量比、刚度比以及外激励频率对压电悬臂梁位移和输出电压的影响曲线发现，系统具有双稳态时曲线的形状要比单稳态时复杂得多，因而会表现出更丰富的运动形式。

选择系统参数中的质量比、刚度比以及外激励参数的频率为分岔参数，利用庞加莱映射分别得到压电悬臂梁的位移和输出电压关于上述参数的分岔图，结果如图8—图13所示，其与图2—图7吻合较好。当分岔参数发生变化时，系统处在单稳态时会从简单周期到混沌再到简单周期的变化，但是当系统处在双稳态时，系统除了有单稳态的分岔过程之外，其中还会发生倍周期分岔以及概周期分岔，并且混沌窗口会随着分岔参数的增大交替出现。即当系统具有双稳态时，系统响应发生分岔产生混沌的可能性更大。

以上分岔现象解释了系统具有双稳态时响应特性更好的原因，同时也得出了系统发生混沌运动的系统参数和激励参数区域，为结构设计中参数值的选择提供了一定理论指导，即尽可能选择分岔点处的值作为系统的参数值。

基于以上关于系统参数和激励参数的分岔分析，选择不同的参数组合，通过Matlab中的ode45求解器，得到的压电悬臂梁的位移时间历程，如图14—图16所示。从图中可以看出，系统的运动既可以发生在零平衡点附近，也可以发生在非零平衡点附近，甚至是在不同的平衡点之间作大幅跃迁，当系统的运动在不同的平衡点之间作大幅跃迁时，其形式不再是简单的周期运动，而是混沌运动。

4结语

本文引入了能引发双稳态现象的磁力模型，首先根据牛顿第二定律以及基尔霍夫第一定律建立了弹性支撑下的压电悬臂梁式振动能量俘获系统的动力学方程。在借助于罗斯-霍尔维茨判据进行了平衡点的静态分岔分析的基础上，利用数值方法对系统进行了动力学仿真分析。直接对无量纲控制微分方程进行数值求解的幅频特性曲线表明系统呈现明显的硬特性，但壓电悬臂梁的振幅随质量比和刚度比的变化却呈软特性。根据数值计算结果基于庞加莱映射给出的分岔图和相轨迹表明在某些参数范围内，系统的简谐周期响应会由于失稳而导致混沌运动。系统的运动既可以发生在零平衡点附近，也可以发生在非零平衡点附近，甚至是在2个不同的非零平衡点之间作大幅跃迁。对比相同参数下系统具有双稳态和单稳态时的电压输出，发现系统具有双稳态时电压输出较高，响应频带相对较宽。虽然上述研究结果可为工程实际中如何优化振动能量采集器提供一定的理论指导，但是取得的成果还停留在数值仿真上面，还需要进一步通过实验进行验证。

参考文献/References：

[1]陈文艺，孟爱华，刘成龙.微型振动能量收集器的研究现状及发展趋势[J].微纳电子技术，2013， 50（11）：715-720.

CHEN Wenyi， MENG Aihua， LIU Chenglong. Research status and developing trend of micro vibration-based energy harvesters[J]. Micronanoelectronic Technology， 2013， 50（11）： 715-720.

[2]刘祥建，陈仁文.压电振动能量收集装置研究现状及发展趋势[J].振动与冲击，2012， 31（16）：169-176.

LIU Xiangjian， CHEN Renwen. Current situation and developing trend of piezoelectric vibration energy harvesters[J]. Journal of Vibration and Shock， 2012， 31（16）： 169-176.

[3]陈仲生，骆彦廷，杨拥民.非线性压电振动能量俘获行为建模及其不同参数影响机理研究[J].国防科技大学学报，2013， 35（2）：154-158.

CHEN Zhongsheng， LUO Yanting， YANG Yongmin. Modeling of nonlinear piezoelectric vibration energy harvesting behaviors and the effects of its different parameters[J]. Journal of National University of Defense Technology， 2013， 35（2）： 154-158.

[4]LUCIANA L S， MARCELO A S， PAULO C M， et al. On the nonlinear behavior of the piezoelectric coupling on vibration-based energy harvesters[J]. Shock and Vibration， 2015： 139381.

[5]周生喜，曹军义，ERTURK A，等.压电磁耦合振动能量俘获系统的非线性模型研究[J].西安交通大学学报，2014， 48（1）：106-111.

ZHOU Shengxi， CAO Junyi， ERTURK A， et al. Nonlinear model for piezoelectric energy harvester with magnetic coupling[J].Journal of Xian Jiaotong University， 2014， 48（1）： 106-111.

[6]MINH S N， YOON Y， OJIN K， et al. Lowering the potential barrier of a bistable energy harvester with mechanically rectified motion of an auxiliary magnet oscillator[J]. Appl Phys Lett， 2017， 111： 253905.

[7]高毓畿，冷永刚，范胜波，等.弹性支撑双稳压电悬臂梁振动响应及能量采集研究[J].物理学报，2014， 63（9）：090501.

GAO Yuji， LENG Yonggang， FAN Shengbo， et al. Studies on vibration response and energy harvesting of elastic-supported bistable piezoelectric cantilever beams[J]. Acta Physica Sinica， 2014， 63（9）： 090501.

[8]孙舒，曹树谦.双稳态压电悬臂梁发电系统的动力学建模及分析[J].物理学报，2012， 61（21）：210505.

SUN Shu， CAO Shuqian. Dynamic modeling and analysis of a bistable piezoelectric cantilever power generation system[J]. Acta Phys Sin， 2012， 61（21）： 210505.

[9]趙健，张国策，陈立群.磁振子压电能量采集器的多尺度分析[J].应用数学和力学，2015， 36（8）：805-813.

ZHAO Jian， ZHANG Guoce， CHEN Liqun. Multi-scale analysis of piezoelectric energy harvesters with magnetic oscillators[J]. Applied Mathematics and Mechanics， 2015， 36（8）： 805-813.

[10]李海涛，秦卫阳.双稳态压电能量获取系统的分岔混沌阈值[J].应用数学和力学，2014， 35（6）：652-662.

LI Haitao， QIN Weiyang. Bifurcation and chaos thresholds of bistable piezoelectric vibration energy harvesting systems[J]. Applied Mathematics and Mechanics， 2014， 35（6）： 652-662.

[11]SAMUEL C S， CLARK C M， BRIAN P M. Nonlinear dynamics for broadband energy harvesting： Investigation of a bistable piezoelectric inertial generator [J]. Physica D： Nonlinear Phenomena， 2010， 239（10）： 640-653.

[12]MEGHASHYAM P， MOHAMMED F D. Characterizing the effective bandwidth of tri-stable energy harvesters[J]. Journal of Sound and Vibration， 2017， 386： 336-358.

[13]PILKEEI K， JONGWON S. A multi-stable energy harvester： Dynamic modeling and bifurcation analysis[J]. Journal of Sound and Vibration， 2014， 333（21）： 5525-5547.

[14]ZHOU S X， CAO J Y， DANIEL J I， et al. Harmonic balance analysis of nonlinear tristable energy harvesters for performance enhancement[J]. Journal of Sound and Vibration， 2016， 373： 223-235.

[15]ZHOU S X， ZUO L. Nonlinear dynamic analysis of asymmetric tristable energy harvesters for enhanced energy harvesting[J]. Communications in Nonlinear Science and Numerical Simulation， 2018， 61： 271-284.

[16]李潇均，王光庆，杨斌强.基于弹性支撑与放大的宽频压电振动能量采集器模型与实验研究[J].传感技术学报，2016， 29（5）：693-700.

LI Xiaojun， WANG Guangqing， YANG Binqiang. Model and experimental researches of a broadband piezoelectric energy harvester with an elastic support and magnifier[J]. Chinese Journal of Sensors and Actuators， 2016， 29（5）： 693-700.

[17]HIDEMI M， YOSHIKAZU T， RUPESH P， et al. Harvesting flow-induced vibration using a highly flexible piezoelectric energy device[J]. Applied Ocean Research， 2017， 68： 39-52.

[18]王祖尧，丁虎，陈立群.两自由度磁力悬浮非线性振动能量采集研究[J].振动与冲击，2016， 35（16）：55-58.

WANG Zuyao， DING Hu， CHEN Liqun. Nonlinear oscillations of a two-degree-of-freedom energy harvester of magnetic levitation[J]. Journal of Vibration and Shock， 2016， 35（16）： 55-58.

[19]HAN X， WANG X， SABU J. A multi-degree of freedom piezoelectric vibration energy harvester with piezoelectric elements inserted between two nearby oscillators[J]. Mechanical Systems and Signal Processing， 2016， 68/69： 138-154.

[20]HAN X， WANG X， SABU J. A dimensionless analysis of a 2DOF piezoelectric vibration energy harvester[J]. Mechanical Systems and Signal Processing， 2015， 58： 355-375.

[21]GATTI G， BRENNAN M J， TEHRANI M G， et al. Harvesting energy from the vibration of a passing train using a single-degree-of-freedom oscillator[J]. Mechanical Systems and Signal Processing， 2016， 66/67： 785-792.

[22]YAN B， ZHOU S X， GRZEGORZ L. Nonlinear analysis of the tristable energy harvester with a resonant circuit for performance enhancement[J]. International Journal of Bifurcation and Chaos， 2018， 28（7）： 1850092.第40卷第3期河北科技大學学报Vol.40，No.3

2019年6月Journal of Hebei University of Science and TechnologyJune 2019