一种用于NS-3仿真的电池模型及其数值解法

金仁成,周峰　李宇

摘要：为了解决网络模拟器NS-3不能对无线传感器网络节点的电池信息做出准确仿真的问题，吸收LiIon电池模型和KiBaM电池模型各自的优点，采用LiIon电池模型的方法计算KiBaM电池模型中有效电荷井的输出电压，得到能够体现电池的速率容量效应和自恢复效应、能够反映输出电压随剩余电量降低而降低的KiBaM-LiIon电池模型，并对模型中无法获得解析解的微分方程组求解，基于隐式Runge-Kutta方法，提出了易于编程实现的数值解法。仿真和实验的结果表明，模型及其数值解法能够在NS-3中对电池使用过程中任何时刻的电压、剩余电量等作出准确预测，且具备计算复杂度低的优点。所提出的电池模型及其数值解法不仅适用于NS-3，同样也适用于其他网络模拟器，可为无线传感器网络和移动Ad-hoc网络的研发提供参考。

关键词：计算机仿真;无线传感器网络;network simulator 3 （NS-3）;电池模型;隐式龙格库塔法

中图分类号：TP39317文献标志码：A

JIN Rencheng，ZHOU Feng，LI Yu.A battery model and its numerical method for the network simulator 3 （NS-3）[J].Journal of Hebei University of Science and Technology，2019，40（3）：233-241.A battery model and its numerical method for the

network simulator 3 （NS-3）

JIN Rencheng， ZHOU Feng， LI Yu

（Key Laboratory for Micro/Nano Technology and System of Liaoning Province， Dalian University of Technology， Dalian， Liaoning 116024， China）

Abstract：In order to solve the problem that the network simulator 3 （NS-3） cannot accurately simulate the battery information of the wireless sensor network （WSN） node， the LiIon battery model is used to calculate the output voltage of the available charge well （ACW） of the KiBaM battery model by combining the advantages of the LiIon battery model and the KiBaM battery model， then a KiBaM-LiIon battery model that can reflect the rate capacity effect and recovery effect of the battery， as well as the decrease of the output voltage with the decrease of remaining charge is proposed. For solving the ordinary differential equations without analytical solution in the model， an easy programming numerical solution based on the implicit Runge-Kutta method is proposed. Simulations and experiments show that the proposed model and its numerical solution can accurately predict the voltage and remaining charge at any time during battery use in NS-3， and have the advantage of low computational complexity. The proposed battery model and proposed numerical solution are not only applicable to NS-3， but also to other network simulators， which provides good technical support and guarantee for the research and development of WSN and mobile Ad-hoc networks （MANET）.

Keywords：computer simulation; wireless sensor network （WSN）; network simulator 3 （NS-3）; battery model; implicit Runge-Kutta

在現代网络通信技术研究中，尤其是大规模网络的研究，在进行网络协议和网络设备的设计、开发及验证时，受设备和场地的限制，通常使用网络模拟技术进行仿真。目前，网络仿真已成为互联网算法性能、协议拓扑最经济快捷的评价方法之一[1]，NS-3（network simulator 3）就是其中一款优秀的网络模拟器。NS-3是一款比较年轻的网络仿真工具，专门用于教育和研究，基于GNU GPLv2许可，可以免费获取、使用和修改[2]。数以万计的科研工作者将自己的科研成果整合进NS-3中，为其面世作出贡献。截止目前，其最新版本为2018-09-04的3.29版本。

对于一些能量受限的网络，例如无线传感器网络（WSNs），移动Ad-hoc网络（MANETs）等，在设计网络协议时需要充分考虑到网络节点的能耗情况[3]。因此，网络模拟器中必须能够提供精确的電池模型，对网络节点的能量消耗进行精确计算，否则仿真结果便是不可信的。

河北科技大学学报2019年第3期金仁成，等：一种用于NS-3仿真的电池模型及其数值解法以无线传感器网络为例，WSN节点通常由不可充电或难以充电的电池进行供电，而大量的研究和实验表明，电池并不是理想的、线性的电荷储存器，而是一个复杂的非线性过程[4]，主要表现在[5-7]：1）电池电压随着放电过程缓慢下降;2）电池能够释放的总电量随着负载电流的增大而减小，该现象被称为电池速率容量效应;3）当电池停止放电或以小电流工作一段时间后，电池的电压反而会上升，该现象被称为电池的恢复特性。为了体现电池的这3种特性，NS-3提供了3种电池模型：理想恒压源模型、LiIon电池模型[8]、RV电池模型[9-10]。理想恒压源模型仅能进行非常粗糙的计算，适用于不受能量因素影响的无线网络仿真中。LiIon电池模型描述了电池电压随放电过程缓慢下降的现象，但并没有体现电池的速率容量效应和自恢复特性。RV电池模型则描述了电池的非线性特性，但并没有考虑到电池电压受剩余电量的影响。

为提高有关能耗相关的仿真准确度，笔者建立了电池的KiBaM-LiIon模型，并给出了该模型适用于NS-3以及其他仿真软件的低计算复杂度的数值解法，最后通过仿真和实验验证了所提出方法的有效性。

1电池模型分析

1.1LiIon电池模型

LiIon电池模型描述了电池在放电过程中的电压下降现象。该模型仅以SoC（state-of-charge，荷电状态）作为输入量，可以精确地预测铅酸蓄电池、锂离子电池、镍镉电池、镍氢电池等符合以下特点的任何种类电池的放电曲线。

1）电池内阻恒定，在充放电过程中不发生太大的改变;

2）充电和放电曲线可逆，在一次充放电循环中不考虑电池的寿命衰减;

3）电池的放电量不与放电电流有关，不考虑电池的非线性特性;

4）电池处于恒温状态;

5）不考虑电池的自放电特性;

6）电池没有记忆效应。

LiIon模型的数学模型如下：V=E-Ri，E=E0-K·qrqr-∫idt+A·e-B·∫idt，A=ef-ee，B=3qe，K=[ef-en+A·（e-Bqn-1）]·qr-qnqn，E0=ef+K+Ri-A，（1）式中：V是输出电压（V）;E是输出电动势（V）;E0是电池恒定电压（V）;K是极化电压（V）;A是指数区域幅度（V）;B是指数区域时间常数倒数（A·h-1）;R是内阻（Ω）;ef是电池初始电压（V）;en是电池名义电压（V）;ee是指数区域结束位置电压（V）;qr是电池额定容量（A·h）;qn是名义区域结束剩余容量（A·h）;qe是指数区域结束剩余容量（A·h）。

放电曲线的指数区域如图1所示。

但是LiIon电池模型没有体现电池的速率容量效应和自恢复特性[11]，因此该模型仅能描述电池在恒流放电条件下的状态，并不适用于类似传感器网络节点这种电源时开时关、负载时大时小的场景。

1.2KiBaM电池模型

NS-3提供了另一种能够描述电池的非线性特性的电池模型：RV电池模型[9-10]。经大量仿真分析发现，RV电池模型实际上就是一种连续的KiBaM电池模型[12-13]。KiBaM电池模型（kinetic battery model）[14]是一种分析模型，具有较高的抽象性。

KiBaM利用2个井（well）来描述电池的特性，如图2所示，2个井分别被称为束缚电荷井（BCW）和可用电荷井（ACW）。ACW直接给负载提供能量，而BCW只能通过一个“狭小”的通道与ACW进行能量交换，能量在通道中的转移速度与两井之间的“高度差”有关，与一个假设的、与电池性质有关的系数有关。该模型通过微分方程组（2）表示。dy1dt=-I+k·（h2-h1），dy2dt=-k·（h2-h1），（2）式（2）中y1为图2中的i，y2为图2中的j，其余符号皆如图2所示。

电池放电时，按照方程组（2）描述，由ACW对外输出能量，ACW的高度h1下降，与BCW之间产生高度差，BCW开始缓慢地向ACW转移能量。如果负载很大，BCW受通道所限来不及向ACW补充能量，ACW能量就已经耗尽，导致电池释放的总能量降低，符合速率容量效应。若在放电一段时间后停止放电，此时BCW仍向ACW缓缓补充能量，刚开始时高度差最大，电池的电量恢复速度也最快，随着过程的进行，两井之间的高度差逐渐缩小直到平衡，外在表现就是电池的电量回升速度越来越慢直到不再恢复[15]，符合电池的自恢复效应。

KiBaM电池模型没有对电池内部的电化学机理建模，而是建立了一个非常有趣的抽象模型，解释了电池的速率容量效应和自恢复效应。但在计算过程中，为了简便却忽略了电池的输出电压与剩余电量之间的关系，将电池看作是恒电压输出，这是十分不准确的。为了得到这种关系，一些文献简单地对输出电压和剩余电量做拟合处理[16]，有效但却缺乏可推广性。

2KiBaM-LiIon电池模型与数值解法

2.1KiBaM-LiIon电池模型

KiBaM模型描述了电池的非线性特性却忽略了电压的变化，而电压的变化正是LiIon模型所着重考虑的，因此可以将2个模型进行结合而弥补各自的缺点。总体思路是：将KiBaM模型的ACW视作是一块单独的电池，使用LiIon模型来计算ACW的对外输出电压。

ACW从初始状态0时刻开始到t时刻之间的电量变化为q（t）=y1（0）-y2（t）。（3）在LiIon模型中有一项∫idt，指的是负载在0时刻到t时刻之间消耗的电量，也可以说是从初始状态0时刻开始到t时刻之间的电量变化，毕竟在不考虑非线性特性的LiIon模型中这两者是相等的。但如果想要用LiIon模型对KiBaM模型的ACW的输出电压进行求解，就必须采用后一种解释，因此要将LiIon模型与KiBaM模型联立，并将其中的∫idt全部替换为式（4）：

V=E-Ri，E=E0-K·qrqr-q（t）+A·e-Bq（t），A=ef-ee，B=3qe，K=[ef-en+A·（e-Bqn-1）]·qr-qnqn，E0=ef+K+Ri-A，dy1dt=-i-ky1c-y21-c，dy2dt=-ky21-c-y1c，q（t）=y1（0）-y2（t），（4）

式中各符號解释同式（1）与式（2）。

2.2用于NS-3的数值解法

KiBaM-LiIon电池模型中有一段微分方程组，微分方程组的解析解一般很难得到，甚至不存在，因此通常对微分方程模型进行数值求解，这是工程领域常见的做法[17]。微分方程的数值解最常用的方法是四阶经典Runge-Kutta解法，但该解法对迭代步长有要求，只有在迭代步长足够小的情况下才能够保证数值稳定性[18]，否则误差急剧增加，掩盖了真值，使计算不能继续迭代下去。举例说明，假如取迭代步长h=0.001的四阶经典Runge-Kutta解法对电池模型进行求解，对一个包含50个节点的网络进行100 s的仿真，单能量部分总计就要进行500万次迭代，这对仿真软件来说是一个巨大的负担，显然是无法令人接受的。

虽然计算精度仍然受迭代步长的影响，但隐式Runge-Kutta解法却有无条件的数值稳定性[19]。只要把隐式解法显化，就可以在NS-3或其他仿真软件中使用。

对于微分方程组：dy1dt=-i-ky1c-y21-c，dy2dt=-ky21-c-y1c。（5）写成矩阵形式dudt=Au+f，（6）其中：A=-kck1-c-k1-ckc，（7）

f=-i0，（8）

u=y1y2。（9）该微分方程组的二级四阶隐式Runge-Kutta解法[20]是：un+1=un+h2（k1+k2），k1=Aun+h4k1+3+2312hk2+f，k2=Aun+h4k2+3-2312hk1+f，（10）式中：向量k1和k2都是隐式的，只需要将这2个向量显化，放在等式的一边，就可以当作是普通表达式在各类仿真软件中进行迭代求解，向量k1和k2的显式表达式为k=（I-C）-1d，（11）其中：k=[k1k2]T，（12）

C=14hA3+2312hA3-2312hA14hA，（13）

d=[Aun+fAun+f]T。（14）根据式（11）到式（14）解出向量k1和k2的显式表达式，Matlab，Mathematica，R语言，Python的SymPy库等支持符号运算的语言都可以实现。本文利用Matlab的solve函数进行求解，最后得到的微分方程组的显式迭代表达式非常长。但得益于隐式解法良好的数值稳定性，可以选用较长的迭代步长，减少迭代次数，因此在迭代次数上减少的运算量远远比公式变长增加的运算量要多。

将解得的向量k1和k2代入式（10），得到微分方程组（5）的数值解迭代式的形式如同式（15）。函数f1和f2同样按照上述Matlab中符号运算功能得到，具体表达式较长不在本文中给出。y1，n+1=f1（y1，n，y2，n），y2，n+1=f2（y1，n，y2，n）。（15）2.3模型在NS-3中的实现方法

NS-3是C++编写的，添加新的模型需要修改源代码。笔者提出的仿真方案是以LiIon电池模型为基础改进而来，因此在编写NS-3的C++代码时以ns3：：LiIonEnergySource类为基础进行修改。ns3：：LiIonEnergySource类的文件地址是src/energy/model/li-ion-energy-source.h和src/energy/model/li-ion-energy-source.cc，在同一文件夹下创建这2个文件的副本，命名为src/energy/model/li-ion-kibam.h和src/energy/model/li-ion-kibam.cc，并且将文件中的类名改为ns3：：LiIonKiBaM，同时构造函数和析构函数的函数名也要做相应的改动。除了名称和表1提到的修改之外，其余均保持ns3：：LiIonEnergySource类的原样不变。

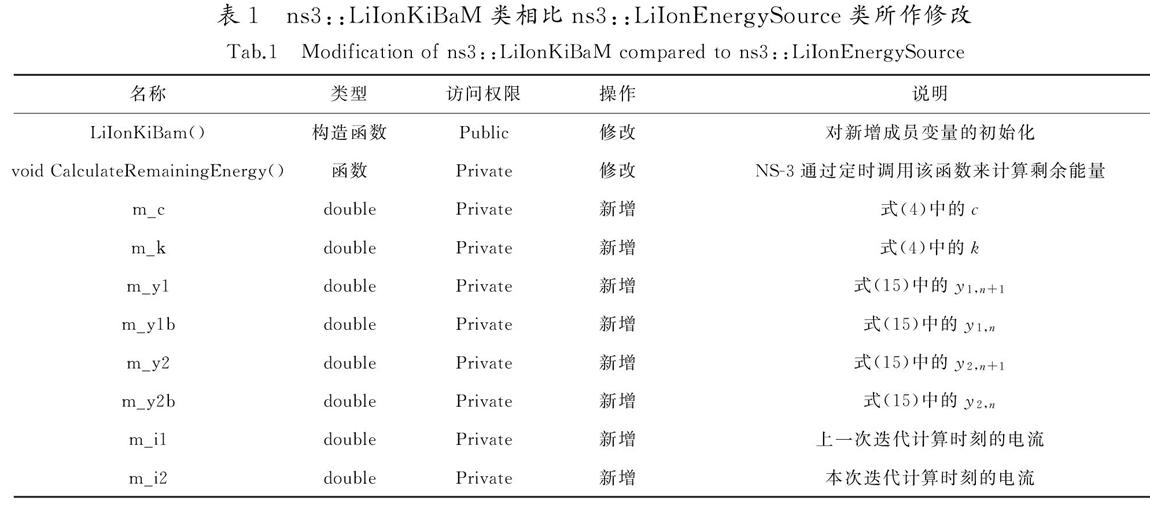
表1ns3：：LiIonKiBaM类相比ns3：：LiIonEnergySource类所作修改

Tab.1Modification of ns3：：LiIonKiBaM compared to ns3：：LiIonEnergySource

名称类型访问权限操作说明LiIonKiBam（）构造函数Public修改对新增成员变量的初始化void CalculateRemainingEnergy（）函数Private修改NS-3通过定时调用该函数来计算剩余能量m_cdoublePrivate新增式（4）中的cm_kdoublePrivate新增式（4）中的km_y1doublePrivate新增式（15）中的y1，n+1m_y1bdoublePrivate新增式（15）中的y1，nm_y2doublePrivate新增式（15）中的y2，n+1m_y2bdoublePrivate新增式（15）中的y2，nm_i1doublePrivate新增上一次迭代计算时刻的电流m_i2doublePrivate新增本次迭代计算时刻的电流

函数CalculateRemainingEnergy（）在函数UpdateEnergySource（）中被调用，UpdateEnergySource（）的函数体结尾通过调用Simulator：：Schedule（）函数来设定UpdateEnergySource（）函数的下一次被调用的时间，达到定时执行的效果。在ns3：：LiIonEnergySource：：CalculateRemainingEnergy（）中仅仅是将剩余能量减去功率与调用间隔的乘积，因为该函数被等时间间隔调用，可以将其改造成迭代计算。图3是修改后的函数ns3：： LiIonKiBaM：：CalculateRemainingEnergy（）主要部分的伪代码和注释。

简便起见，本文没有编写该能量模型的Helper类，因此在给设备指定能量模型时，需要先用ns3：：CreateObject（）模版函数分别创建ns3：：EnergySourceContainer类和ns3：：LiIonKiBaM类的实例，然后调用EnergySourceContainer：：Add（）函数，将指向ns3：：LiIonKiBaM实例的指针添加到ns3：：EnergySourceContainer的实例中。

3仿真与实验评价

3.1数值解法的仿真评价

用仿真的方式来评价本文2.2节提出的数值解法性能，仿真平台是Matlab R2018a 64位版。由于仅仿真数值解法的性能，为了排除模型因素的影响，采用提出的数值解法对原始的KiBaM模型进行求解。电池电压3.7 V，电池容量200 A·s，放电状态是10 s，往复周期2 A电流间歇放电。选取Matlab提供的迭代步长0.001 s的ode求解器作为对比基准，这是在无法得到解析解的条件下所能达到的最好精度的微分方程数值解[21]。作为对比，迭代步长0.1 s的四阶经典Runge-Kutta解法和迭代步长1 s的本文提出的解法进行比较，仿真结果如图4所示。

从仿真结果可以看出，即使求解精度提高了10倍，经典Runge-Kutta解法的误差仍然比二级四阶隐式Runge-Kutta解法要大。提出的解法以经典解法1/10的求解精度，得到了标准差仅为经典解法32.27%的准确结果、最大偏差仅为经典解法26.98%的准确结果。且经典方法存在严重的累积误差问题，随着仿真时间的推移，累积误差会越来越大，最终得到发散的结果。而本文2.2节提出的解法具有更小的计算开销和更高的求解精度，如表2所示。

方法标准差最大偏差终点偏差经典解法4.301 510.434 610.434 6本文提出的解法1.388 42.815 61.517 9

3.2电池模型的实验评价

为了体现模型的泛用性，被测电池为2块不同的电池，标称电压均为3.7 V，标称容量均为600 mA·h，但内阻等其他参数不同。测量仪器为EBC-A05+电池测试仪、安捷伦34401A数字万用表，如图5所示。

从电池电量充满的状态开始，分别以恒流1，05，0.25，0.1 A和間歇0.1 A的负载进行实验并记录每时刻的电压值，并在NS-3中分别进行上述同条件仿真。由于NS-3不具备图形界面，没有绘图功能，所以需要把NS-3的输出数据拷贝到windows计算机并在Matlab中读取，才能绘出电池在放电过程中的实测曲线和仿真曲线。为了评价仿真的准确度，在曲线中等间距取3 000个点，定义它们的均方根误差（RMSE）作为评价标准，实验结果如表3和图6所示。

实验条件均方根误差/V最大偏差/V电池一1 A恒流放电0.050 90.088 5电池一0.5 A恒流放电0.037 70.172 7电池一0.25 A恒流放电0.040 20.494 2电池一0.1 A恒流放电0.049 60.520 9电池一0.1 A间歇放电0.031 90.100 0电池二0.25 A恒流放电0.029 60.258 5电池二0.5 A恒流放电0.030 30.158 4电池二1 A恒流放电0.056 10.085 9

由实验结果可知，该电池模型能够精准地描述任意电池在使用过程中的状态，平均误差0.04～0.05 V。最大偏差出现在电池即将耗尽阶段，但在实际使用时，节点不会将电量耗尽，而是会在即将耗尽电量时退出网络，所以这种较大误差的情况实际上是没有影响的，进一步说明本文提出的电池模型的准确度较高。

4结语

笔者提出的电池模型及其数值解法解决了在NS-3中无线传感器网络和移动Ad-hoc网络仿真过程中对节点能耗估计不准确的问题，其有效性和准确性得到了实验的证明和支持。它不仅适用于NS-3，同样也适用于其他网络模拟器，为无线传感器网络和移动Ad-hoc网络的研究与发展提供了良好的技术支持和保障。但该电池模型没有考虑电池的寿命衰减，忽略了电池随长期使用而出现的老化现象，需针对此问题进一步深入研究。

参考文献/References：

[1]茹新宇，刘渊. 网络仿真器NS3的剖析与探究[J]. 计算机技术与发展，2018，28（3）：72-77.

RU Xinyu， LIU Yuan. Analysis and research on network simulator 3[J]. Computer Technology and Development， 2018， 28（3）： 72-77.

[2]顾洁，朱宗卫，徐友庆，等. NS-3仿真环境中802.11服务区分机制的研究与实现[J]. 计算机工程，2018：0051676.

GU Jie， ZHU Zongwei， XU Youqing， et al. Research on the service differentiation mechanisms in wireless local area networks by using NS-3[J]. Computer Engineering， 2018： 0051676.

[3]CHE Zhiping， JIN Rencheng， ZHU Ming， et al. Battery optimal scheduling based on energy balance in wireless sensor networks[J]. IET Wireless Sensor Systems， 2015， 5（6）：277-282.

[4]王震. 基于双能源的高效节能WSN节点设计[D]. 大连：大连理工大学， 2015.

WANG Zhen. The Design of Efficient Energy-Saving WSN Node Based on Dual-Energy[D]. Dalian：Dalian University of Technology， 2015.

[5]LAHIRI K， RAGHUNATHAN A， DEY S， et al. Battery-driven system design： A new frontier in low power design[C]// International Conference on Design Automation Conference. [S.l.]：IEEE， 2002：994932.

[6]许参，李杰，王超. 一种高效的多电池系统放电方法[J].电路与系统学报， 2005，10（5）： 144-148.

XU Shen， LI Jie， WANG Chao. A effective multiple battery system discharge schedule[J]. Journal of Circuits and Systems， 2005，10（5）： 144-148.

[7]鲍曜. 一种低功耗网络控制收发系统的设计与研究[D]. 杭州：浙江大学，2017.

BAO Yao. The Design and Research of A Low-power Network Control Mail System[D]. Hangzhou：Zhejiang University， 2017.

[8]TREMBLAY O， DESSAINT L A， DEKKICHE A I. A generic battery model for the dynamic simulation of hybrid electric vehicles[C]// Vehicle Power and Propulsion Conference.[S.l.]： IEEE， 2007：4544139.

[9]RAKHMATOV D N， VRUDHULA S B K. An analytical high-level battery model for use in energy management of portable electronic systems[C]// IEEE/ACM International Conference on Computer Aided Design. [S.l.]：IEEE， 2001：968687.

[10]RAKHMATOV D N， VRUDHULA S B K. Energy management for battery-powered embedded systems[J]. ACM Transactions on Embedded Computing Systems， 2003， 2（3）：277-324.

[11]張彦琴， 刘汉雨， 卢明哲. 锂离子电池统一充电模型研究[J]. 电源技术， 2015， 39（2）：283-284.

ZHANG Yanqin， LIU Hanyu， LU Mingzhe. Modeling of unified charging of lithium-ion batteries[J]. Chinese Journal of Power Sources， 2015， 39（2）： 283-284.

[12]JONGERDEN M， HAVERKORT B R. Which battery model to use？[J]. IET Software， 2010， 3（6）：445-457.

[13]MANWELL J F， MCGOWAN J G. Lead acid battery storage model for hybrid energy systems[J]. Solar Energy， 1993， 50（5）：399-405.

[14]RAO V， SINGHAL G， KUMAR A， et al. Stochastic battery model for embedded systems[C]// Proceedings of the IEEE International Conference on VLSI Design.[S.l.]： IEEE， 2005：61.

[15]王闯. 锂电池SOC估算方法及串联电池组一致性研究[D]. 沈阳：东北大学，2014.

WANG Chuang. Lithium-ion Battery SOC Estimation Method and the Equilibrium of Series Battery Pack Research[D]. Shenyang：Northeastern University， 2014.

[16]余文正. 动力电池模型分析及其快速充放电策略研究[D]. 成都：电子科技大学，2013.

YU Wenzheng. Power Battery Model Analysis and Its Fast Charge and Discharge Strategy Study[D]. Chengdu：University of Electronic Science and Technology of China， 2013.

[17]倪素环，杨雪. 冲击振动单边单质量破碎系统的非线性动力学分析[J]. 河北科技大学学报，2017， 38（5）：469-473.

NI Suhuan， YANG Xue. Nonlinear dynamic analysis of single-sided and single-mass crushing system under impact and vibration[J]. Journal of Hebei University of Science and Technology， 2017， 38（5）：469-473.

[18]张宏伟. 计算机科学计算[M]. 北京：高等教育出版社，2013.

[19]CHEN D J L. The efficiency of Singly-implicit Runge-Kutta methods for stiff differential equations[J]. Numerical Algorithms， 2014， 65（3）：533-554.

[20]BUTCHER J C. Implicit runge-kutta processes[J]. Mathematics of Computation， 1964， 18：50-64.

[21]马泽涛，文鹏，施琳达，等. 基于Matlab常微分方程数值解的分析与比较[J]. 大学教育， 2017（12）：50-52.第40卷第3期河北科技大学学报Vol.40，No.3

2019年6月Journal of Hebei University of Science and TechnologyJune 2019