微凹槽参数对轴承润滑性能影响的显著程度分析

巩加玉，金勇，刘正林，王焕杰，周建辉

(1. 武汉理工大学 能源与动力工程学院，武汉 430063；2. 武汉船舶职业技术学院，武汉 430050；3. 中国船舶研究设计中心，武汉 430064)

水润滑轴承因具有绿色环保、节约资源和结构简单等优点，广泛应用于船舶和水下航行器中。但由于水的黏度较低，导致水润滑轴承的承载能力较小，容易引起轴承异常磨损、振动和噪声。

为提高轴承的润滑性能，国内外学者提出采用表面织构技术(surface texture)对轴承内表面进行改性处理[1-4]，并利用试验、成熟的有限元软件或简化的轴承模型对微凹槽轴承进行分析研究。文献[5-6]研究了微凹槽界面形状对轴承润滑性能的影响，结果表明，矩形截面微凹槽润滑效果明显优于其他形状截面；文献[7]建立了二维CFD模型，研究发现，凹槽的数量越多和尺寸越小，其承载力就越大，但对摩擦因数影响较小；文献[8]发现,在较低接触压力下,垂直于滑动方向的微凹槽具有更好的减摩能力。

基于以上研究成果，现分析微凹槽的深度、宽度、长度、布置位置及截面形状5种因素对水润滑轴承润滑性能影响的显著程度。

1 润滑模型的建立

1.1 润滑模型

微凹槽轴承润滑模型如图1所示。图中：R和r分别为轴承内半径和主轴半径；O1和O2分别为轴承和主轴的圆心；e为偏心距；θ为偏位角；hmin和hmax分别为最小、最大膜厚；φ为从最大膜厚处开始的周向坐标；ψ和γ分别为微凹槽区域的周向起始角和周向布置范围；Wt，Lt和Dt分别为微凹槽的宽度、轴向长度和深度；F为作用在主轴上的径向载荷；n为转速；Pt为微凹槽的跨距。

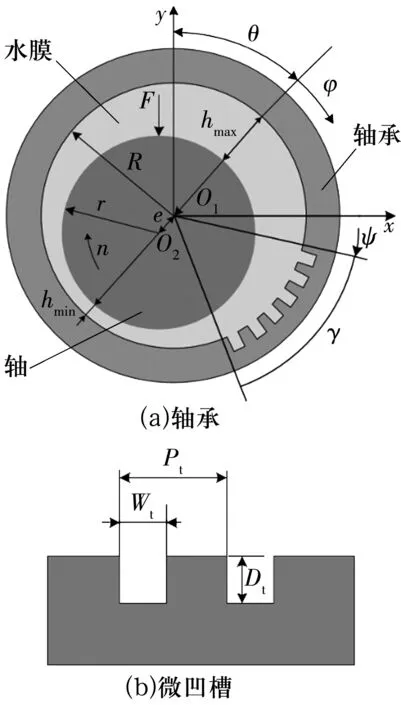
图1 微凹槽轴承示意图

基于文献[9-10]介绍的轴承润滑基本理论，建立水润滑微凹槽轴承流-固耦合模型，其中轴承弹性变形采用柔度矩阵法求得，水膜压力采用超松弛迭代法求解，计算过程中水膜压力收敛精度为1.0×10-3。

1.2 模型验证试验

为验证所建润滑模型的正确性，设计了水润滑微凹槽轴承板条试验。试验平台采用某公司研发的JXH-C液体动压滑动轴承试验台，其结构如图2所示。

1—摩擦力传感器；2—加载力传感器；3—压力传感器；4—转速传感器；5—温度传感器；6—控制台；7—直流电动机；8—三角带

在实际工作过程中，主轴与轴承的接触区主要集中在底部40°～60°范围内。因此，为了保证微凹槽轴承板条能形成动压润滑，且考虑到试验台和织构加工技术的限制，故采用周向60°的轴承板条取代整体轴承进行试验。板条基体采用6061铝合金，板条内衬采用赛龙材料。试验过程中板条布置在主轴上方，故加载力须计入板条和传感器等的质量，共1 206 g。为了测量水膜压力，在板条轴向对称面内均匀布置3个HM91A-H1-2-V2-F1-W1压力传感器，间距为20°，量程为0～2 MPa，精度为0.025%。试验板条设计2组，分别为无微凹槽板条和局部微凹槽板条。局部微凹槽板条是入口边至周向30°范围内均匀加工矩形截面轴向贯穿型微凹槽，微凹槽板条轴承的结构参数见表1。试验过程中施加的径向载荷为12 N，主轴转速为300～1 400 r/min，间隔100 r/min。

表1 轴承参数

径向载荷12 N下，2组板条的摩擦因数f随转速的变化曲线如图3所示。图中A，B分别为无微凹槽和局部微凹槽两曲线的拐点。

图3 摩擦因数随转速的变化曲线

由图3可知，当主轴转速大于1 200 r/min时，无微凹槽板条进入动压润滑状态；转速大于1 300 r/min时，局部微凹槽板条进入动压润滑状态。为了论证所建润滑模型的正确性，在径向载荷12 N，转速1 400 r/min下进行试验，测得2组板条轴向对称面内的水膜压力，并与仿真压力分布对比，结果如图4所示。

图4 仿真与试验水膜压力

由图4a可知，无微凹槽板条试验压力与仿真压力的最大误差为7.4%；由图4b可知，局部微凹槽板条试验压力与仿真压力的最大误差为8.3%。由于存在模型误差和测量误差，导致试验与仿真压力不完全一致，但最大误差均小于10%，满足计算精度要求，证明了所建润滑模型的正确性。

2 数值计算与分析

水润滑微凹槽轴承的仿真计算以工作环境最为恶劣的下半轴承为对象，轴承结构参数见表1，内衬材料为赛龙，微凹槽间距固定为2 mm，轴承偏心率为0.3，主轴转速为1 000 r/min。

经网格数量无关性检验，仿真计算网格数量采用周向400个，轴向50个的形式。

2.1 全微凹槽轴承正交仿真

为了分析微凹槽的深度、宽度、长度及截面形状4种因素对水润滑全微凹槽轴承润滑性能影响的显著程度，针对上述4种因素各选择了3个因素水平，设计了4因素3水平的L9(34)正交表，见表2。微凹槽截面如图5所示。根据正交表中的9种工况，分别仿真计算量纲一的承载力和摩擦因数，并对结果进行极差分析，绘制相应的效应曲线图。

图5 微凹槽截面

表2 全微凹槽轴承正交仿真因素及水平

2.1.1 承载力为正交仿真指标

水润滑全微凹槽轴承量纲一的承载力和极差分析结果见表3，对应的效应曲线如图6所示。

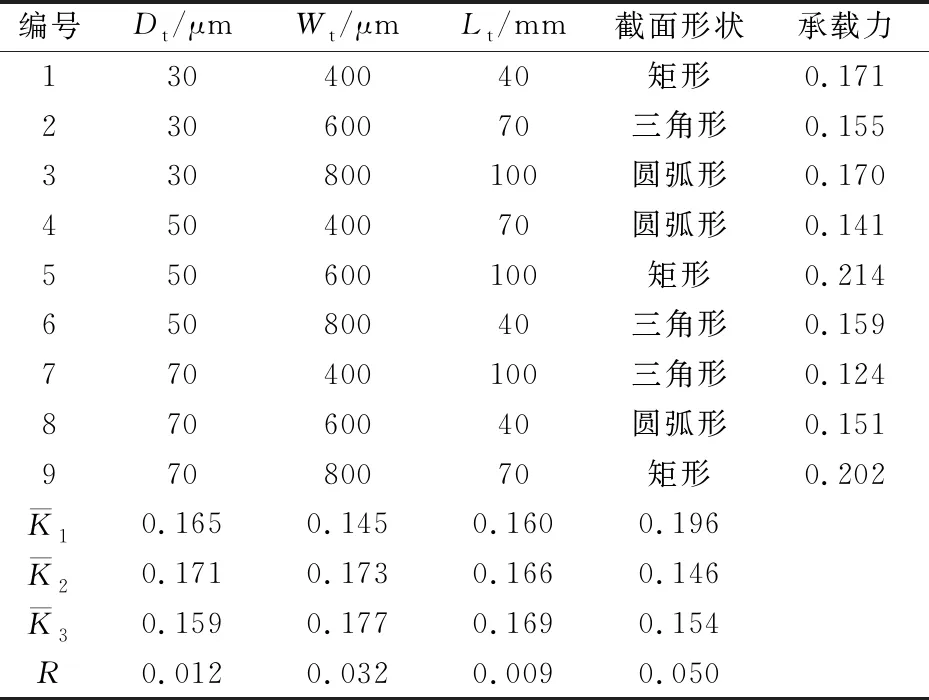
表3 全微凹槽轴承承载力和极差分析结果

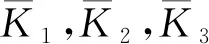
(1)

(2)

由表3和图6可知：

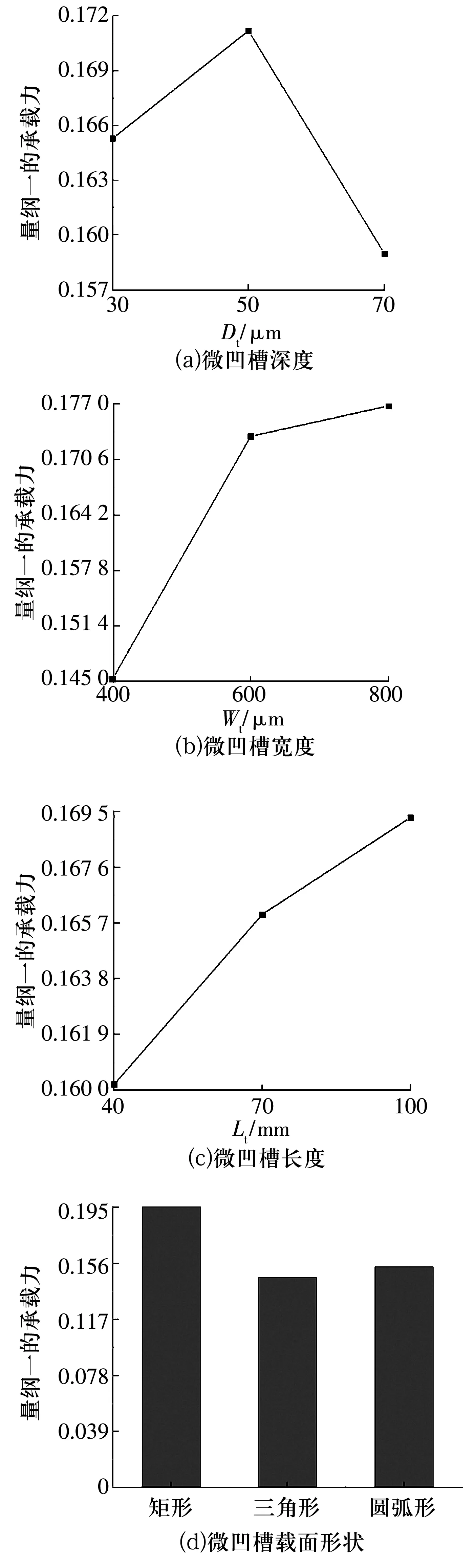
图6 全微凹槽轴承中以量纲一的承载力为指标的效应曲线图

1)全微凹槽的深度、宽度、长度及截面形状4因素对水润滑轴承承载力影响的显著程度顺序为：截面形状>宽度>深度>长度。

2)当水润滑下半轴承采用全微凹槽时，提高轴承承载力效果最好的微凹槽结构参数组合为深度50 μm，宽度800 μm，长度100 mm，矩形截面。仿真计算得到最佳组合时的量纲一的承载力为0.236，大于表3所示的所有承载力。

3)就提高轴承承载力而言，微凹槽深度效果最好的是50 μm，其次为30,70 μm；在间距2 mm不变的情况下，微凹槽宽度效果最好的是800 μm，最差的是400 μm；微凹槽长度效果最好的是100 mm，最差的是40 mm；微凹槽截面效果最好的是矩形界面，最差的是三角形截面，这与文献[5-6]的结论一致。

2.1.2 摩擦因数为正交仿真指标

以水润滑全微凹槽轴承摩擦因数为正交仿真指标的效应曲线如图7所示。

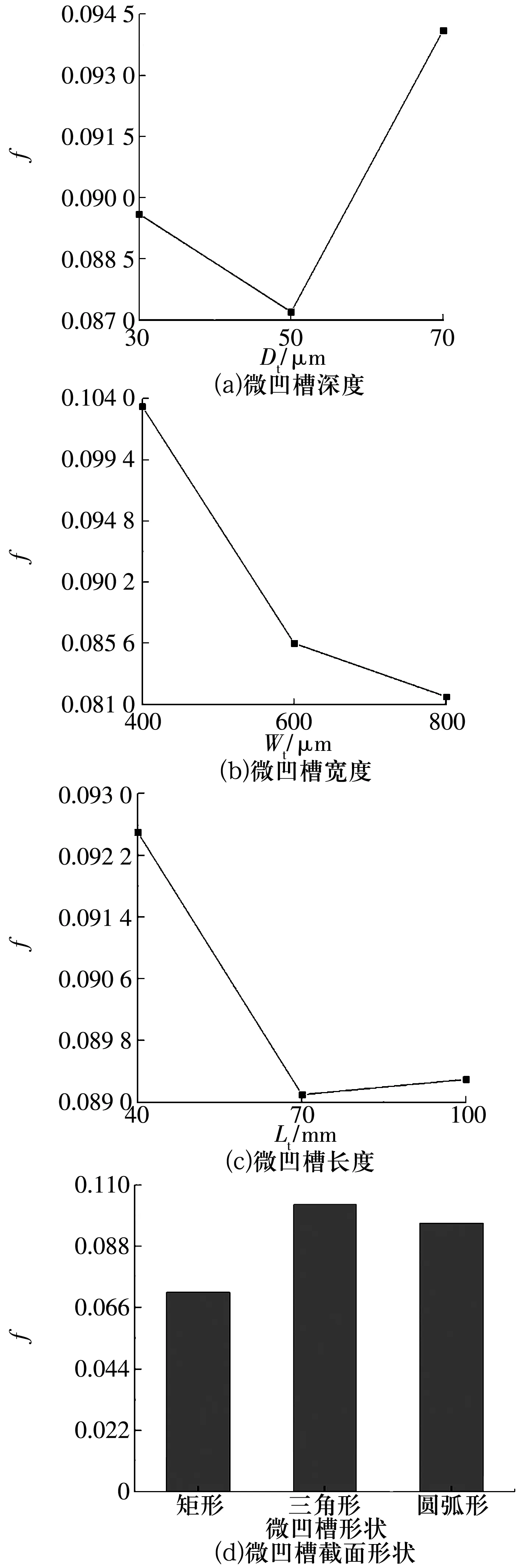
图7 全微凹槽轴承中以摩擦因数为指标的效应曲线图

由图7可知：

1)全微凹槽的深度、宽度、长度及截面形状对摩擦因数影响的显著程度顺序为截面形状>宽度>深度>长度。

2)减小水润滑下半轴承摩擦因数效果最好的微凹槽结构参数组合为深度50 μm，宽度800 μm，长度70 mm，矩形截面。微凹槽最佳组合时的摩擦因数仿真结果为0.055 1，小于图7中的所有摩擦因数。

3)微凹槽深度为50 μm时的摩擦因数最小，深度为70 μm时最大；在间距2 mm不变的情况下，微凹槽宽度为800 μm时的摩擦因素最小，宽度为400,600 μm时的较大；微凹槽长度为70 mm时摩擦因数最小；微凹槽截面为矩形截面时的摩擦因数比三角形截面和圆弧形界面的小，这与文献[5-6]的结论一致。

对比图6和图7可知，微凹槽的深度、宽度、长度及截面形状对轴承承载力和摩擦因数影响的显著程度一致，但微凹槽提高轴承承载力和降低轴承摩擦因数的最佳参数组合并不一致。

2.2 局部微凹槽轴承正交仿真

为了分析微凹槽的深度、宽度、长度、截面形状及布置位置5种因素对水润滑局部微凹槽轴承润滑性能影响的显著程度，设计了5因素3水平的L18(35)正交表，见表4。微凹槽布置位置如图8所示。对正交表中的18种工况下量纲一的承载力和摩擦因数进行仿真计算，并对结果进行极差分析，绘制相应的效应曲线图。

图8 微凹槽布置位置

2.2.1 承载力为正交仿真指标

水润滑局部微凹槽轴承承载力和极差分析结果见表5。对应的效应曲线如图9所示。

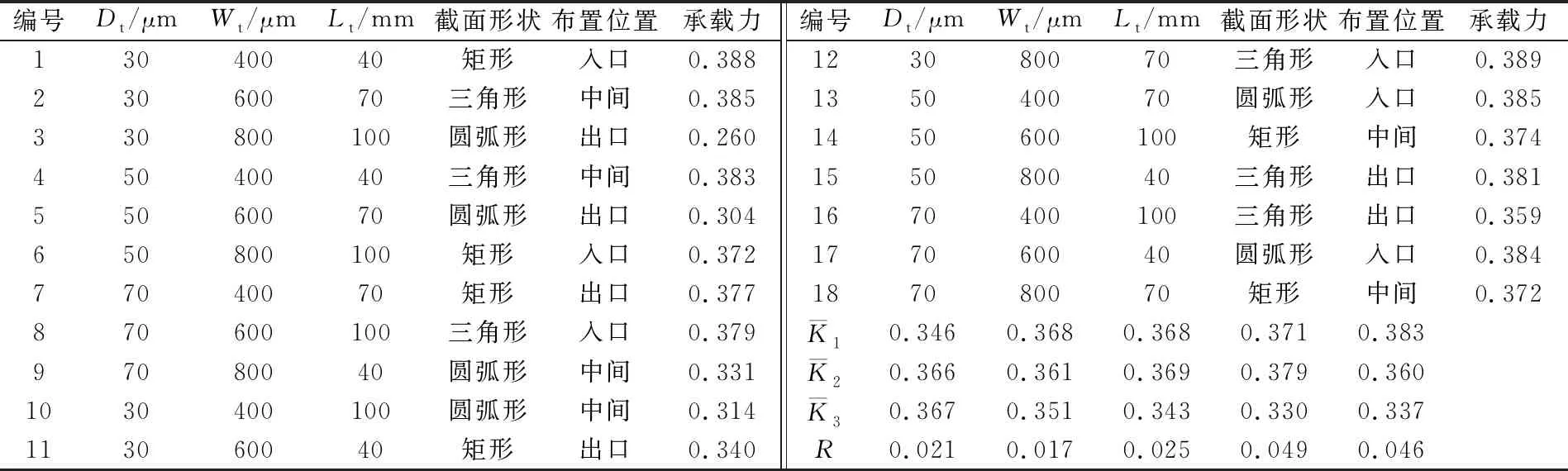
表5 局部微凹槽轴承承载力和极差分析结果

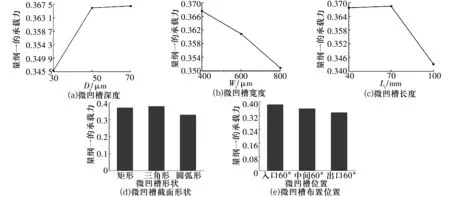
图9 局部微凹槽轴承以量纲一的承载力为指标的效应曲线图

由表5和图9可知：

1)局部微凹槽的深度、宽度、长度、截面形状及布置位置5因素对轴承承载力影响的显著程度顺序为截面形状>布置位置>长度>深度>宽度。

2)当水润滑下半轴承采用局部微凹槽时，提高轴承承载力效果最好的微凹槽结构参数组合为深度70 μm,宽度400 μm,长度70 mm,三角形截面,布置位置入口60°。仿真计算得到最佳组合时的量纲一的承载力为0.395，大于表5中所有量纲一的承载力。

3)微凹槽深度为70 μm时的承载力比深度为30，50 μm时的大；在微凹槽间距为2 mm的情况下，微凹槽宽度为400 μm时的承载力最大，深度为800 μm时的承载力最小；微凹槽长度为70 mm时的承载力最大；微凹槽截面形状中，矩形和三角形截面相较圆弧截面承载力要大；微凹槽布置在入口及中间时的承载力大于微凹槽布置在出口时的承载力。

2.2.2 摩擦因数为正交仿真指标

以摩擦因数为正交仿真指标时的效应曲线如图10所示。

图10 局部微凹槽轴承以摩擦因数为指标的效应曲线图

由图10可知：

1)局部微凹槽的深度、宽度、长度、截面形状及布置位置对摩擦因数影响的显著程度顺序为截面形状>布置位置>深度>长度>宽度。

2)减小水润滑下半轴承摩擦因数效果最好的微凹槽结构参数组合为深度70 μm,宽度400 μm,长度70 mm,三角形截面,布置位置入口60°。仿真计算得到最佳组合时的摩擦因数为0.036 2，小于图10所示的所有摩擦因数。

3)在微凹槽深度中，减摩效果最好的是70 μm；在微凹槽间距为2 mm的情况下，微凹槽宽度减摩效果最好的是400 μm，最差的是800 μm；微凹槽长度减摩效果最好的是70 mm，其次为40 mm；矩形截面和三角形截面微凹槽减摩效果最好；微凹槽布置在入口时局部微凹槽轴承摩擦因数最小，布置在出口时摩擦因数最大。

对比图9和图10可知，微凹槽的深度、宽度、长度、截面形状及布置位置对轴承承载力和摩擦因数影响的显著程度不完全一致，微凹槽提高轴承承载力和降低轴承摩擦因数的最佳参数组合也不一致。

3 结论

1)对于全微凹槽轴承，微凹槽参数对轴承承载力和摩擦因数影响的显著程度为：截面形状>宽度>深度>长度。

2)对于局部微凹槽轴承，微凹槽参数对轴承承载力影响的显著程度为：截面形状>布置位置>长度>深度>宽度，织构参数对轴承摩擦因数影响的显著程度为：截面形状>布置位置>深度>长度>宽度。

本研究对于完善水润滑微凹槽轴承的设计提供参考，但由于仅考虑了单个偏心率和微凹槽间距，并未考虑偏心率和微凹槽间距的综合作用，在未来的研究中有待进一步完善。