基于CEEMDAN和排列熵的滚动轴承故障诊断方法

白丽丽，韩振南，任家骏，秦晓峰

(太原理工大学 机械工程学院，太原 030024)

作为旋转机械中的关键部件，滚动轴承是设备正常且高效运行的保障。为确保轴承运行时的高可靠性，保持主机的低停机时间，快速、准确、方便地检测出轴承故障的类型及其严重程度具有重要意义[1]。

在过去的几十年中，基于振动的分析方法在时域、频域和时频域中得到了很好的发展。考虑到设备的运行通常伴随着摩擦、振动和冲击，振动信号会呈现出一些非线性和非平稳性等特征[2-3]，在机械故障诊断领域中出现了许多非线性的分析方法。这些方法具有一定的优势，但缺点也不容忽视。比如，近似熵[4]严重依赖数据的记录长度，不利于潜在故障的及时发掘；样本熵[5]基于Heaviside阶跃函数，而该函数在边界上是突变且不连续的；模糊熵[6]利用隶属函数的概念进行定义，其结果往往不够精确。因此，排列熵(Permutation Entropy，PE)作为测量时间序列的随机性和动态变化的非线性参数被引入故障诊断领域，其利用相邻值的比较分析时域数据的复杂性[7]，具有计算简单，速度快，对非线性单调变换的鲁棒性和稳定性好的优点，能有效地检测和放大振动信号的动态变化，表征机械在不同工况下的工作状态[8]。

完整自适应噪声集成经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise，CEEMDAN)克服了EMD和EEMD的缺点[9]，其在分解的每个阶段都加入了特定噪声而不是高斯白噪声。因此，当得到唯一剩余时，真正的IMF被定义为当前剩余数与其局部均值之间的差值。CEEMDAN的迭代次数是EEMD的一半，并能准确实现信号的分解。考虑到CEEMDAN处理得到的IMF代表了信号中嵌入的自然振荡模式[10]，提取IMF的PE值(IMP-PE)作为特征矩阵就可以用于揭示振动信号的局部多尺度特性，可以为故障诊断提供更准确、全面的信息。

粒子群寻优支持向量机(Support Vector Machine Optimized by Particle Swarm， PSOSVM)通过粒子群方法寻找适合SVM的最优参数[11]，较好地解决了人工神经网络的过拟合和局部最优解问题，可在特征提取后实现故障的自动诊断，提高故障检测精度。

综上，提出了CEEMDAN与PE有机结合的特征提取算法，并利用PSOSVM形成了有效的智能故障诊断方法。

1 CEEMDAN原理

CEEMDAN算法的流程如图1所示，主要分以下步骤。

1)在原始信号x中加入Ek(w(i))，即

x(i)=x+βk-1Ek(w(i))，

(1)

式中：Ek(w(i))为由EMD处理高斯白噪声的第k个IMF；Ek(·)为由EMD处理产生的第k个模态的运算符；w(i)为增加的第i个高斯白噪声；系数βk-1=ε0std(rk)，为每个阶段的信噪比。

2)利用EMD计算x(i)的局部均值，得到第1个残差r1

(2)

式中：N为总集合数；M(·)为产生信号局部均值的运算符，E1(x)=x-M(x)。

3)计算第1个IMF得

(3)

4)分解r1+β1E2(w(i))并定义第2个IMF，即

(4)

5)计算第k个残差rk

(5)

6)获得第k个IMF

(6)

7)重复第5和第6步，直到R满足终止条件

(7)

因此，信号x可以表示为

(8)

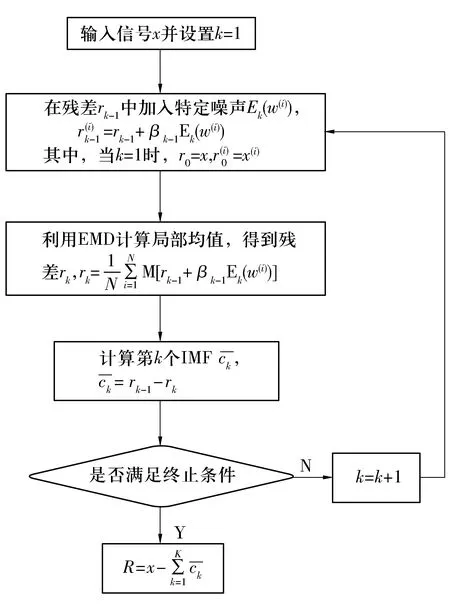
图1 CEEMDAN算法流程图

2 PE原理

熵用于描述时间序列的不规则性和复杂性，通过比较信号熵某些特征的变化情况，可以直接判断信号的组成变化。PE的计算过程如下。

将序列{x(i),i=1,2,…,N}在相空间中重构

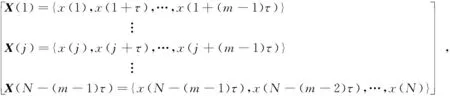
(9)

式中：m为嵌入维数；τ为嵌入延迟时间。

PE就是序数型概率分布估计的Shannon熵

(10)

(11)

显然，Hp∈(0,1)，其大小表示时间序列的随机程度。Hp越小，时间序列越规则；反之，时间序列将越随机。

3 故障诊断机理

当轴承发生故障时，振动信号的时域波形会产生脉冲，PE可以衡量时间序列的复杂性，但无法找出引起异常工作状态的原因，而CEEMDAN可以根据信号的局部特征自适应地将信号分解成一系列包含振动信号故障特征的IMF。因此，IMF-PE可以从多个尺度很好地揭示这些隐藏的故障特征，为故障诊断提供准确的信息。

设正常轴承与故障轴承的仿真信号分别为

x1(k)=sin(2πf1kT)+2sin(2πf2kT)，

(12)

x2(k)=e-at′[(sin(2πf1kT)+2sin(2πf2kT)]，

(13)

式中：t′=mod(kT,1/fm); 指数频率a=300；调制频率fm=500 Hz;载波频率f1=1 000 Hz，f2=3 000 Hz；采样间隔T=1/20 000 s。加入随机噪声后得到如图2所示的时域波形。

图2 仿真信号的时域波形

将仿真信号进行CEEMDAN处理得到一系列IMF，分别计算每个IMF的PE值，结果如图3所示。从图中可以看出：正常信号和故障信号的IMF-PE值均随着信号的进一步分解而降低，频率较高的IMF往往表现出较高的复杂程度，且故障信号的脉冲主要分布在前几个IMF中；故障信号的IMF-PE值基本高于正常信号的IMF-PE值，表明IMF-PE的分布可以反映一个时间序列的特征，从而可以用来区分不同类型的信号。

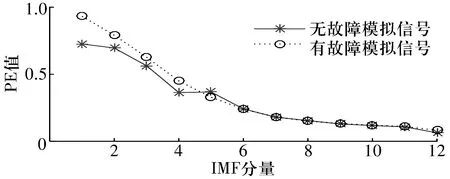
图3 仿真信号的IMF-PE值

根据以上分析，确定如图4所示的故障诊断流程：首先，利用CEEMDAN将振动信号分解为一系列IMF；然后，计算前5个IMF的PE值并形成一个特征矩阵；最后，将该特征矩阵输入PSOSVM进行训练，区分振动信号的故障类型及故障严重程度。

图4 故障诊断流程

4 试验验证

4.1 西储大学数据验证

试验轴承为6205-2RS型深沟球轴承，利用电火花加工不同直径的单点故障，电动机转速为1 797 r/min，采样频率为12 kHz，驱动端轴承的详细分类信息见表1。

每一类别各取150个样本，依次计算这1 500个样本的PE值，结果如图5所示，从图中可以看出：前150个样本属于正常状态，其PE值明显小于故障轴承的PE值，且均小于0.7；对于故障工况下的1 350个样本，无论故障类型和故障严重程度有何区别，其PE值均大于0.7。试验结果说明PE值是可以反映振动信号微小变化的敏感参数，PE值越大，振动信号含有故障的可能性就越大。虽然通过PE值可以判别轴承有无故障，但无法识别具体的故障类型及故障严重程度，这就需要提取更多的特征参数，并利用故障分类器识别轴承的运行状态。

图5 所有分类样本的PE值

将上述1 500个样本分别进行CEEMDAN处理生成一系列的IMF，计算每个样本的前5个IMF-PE值得到一个1 500×5的特征矩阵，将该特征矩阵输入PSOSVM中进行样本训练(每类75个样本)及模式识别(每类75个样本)，进行10次运算得到的平均识别率高达99.8%，说明该特征矩阵能够很好地反映轴承的故障类型及故障严重程度。

为展示IMF-PE方法的有效性和优越性，与其他特征提取方法的识别率进行对比，结果见表2，由表可知：文献[12-14]在正常、钢球故障、内圈故障和外圈故障这4种分类状态下可以得到较高的识别率，但其只能区分不同的故障类型，而没有对故障严重程度进行区分；文献[6,15-17]均对故障类型和故障严重程度进行了对比,可以看出IMF-PE方法在考虑众多故障类型时，在保证算法简单和分类种类多的优势下，仍然得到满意的识别率。

表2 不同特征提取方法的识别率

4.2 自建试验台数据验证

轴承故障模拟试验台由驱动装置、加载机构、固定装置和机座组成。试验轴承为2612圆柱滚子轴承，滚子直径为18 mm，滚子组节圆直径为95 mm，滚子数为12，接触角为0°。试验台转速为1 420 r/min，采样频率为2 000 Hz，详细的故障分类情况参见表3，其中轻载为加载100 N·m的扭矩，重载为加载1 000 N·m的扭矩。

表3 实测滚动轴承的故障分类信息

每组故障类型取150个样本，将得到的1 200个样本分别进行CEEMDAN处理，然后取每组样本的前5个IMF-PE构成1 200×5的特征矩阵，取每个样本的前3组特征构建的散点图如图7所示，从图可以非常直观地看出，通过CEEMDAN处理后，前3个IMF-PE就可以基本区分轴承的故障状态。

图7 前3个特征元素形成的散点图

将每类中的75个样本输PSOSVM进行训练，其余用于测试，识别结果见表4。由表可知：经CEEMDAN处理后形成的IMF-PE特征向量有着相当高的平均测试精度，当前5个IMF-PE形成的特征矩阵全部输入PSOSVM后，故障类型的识别率可以达到100%。

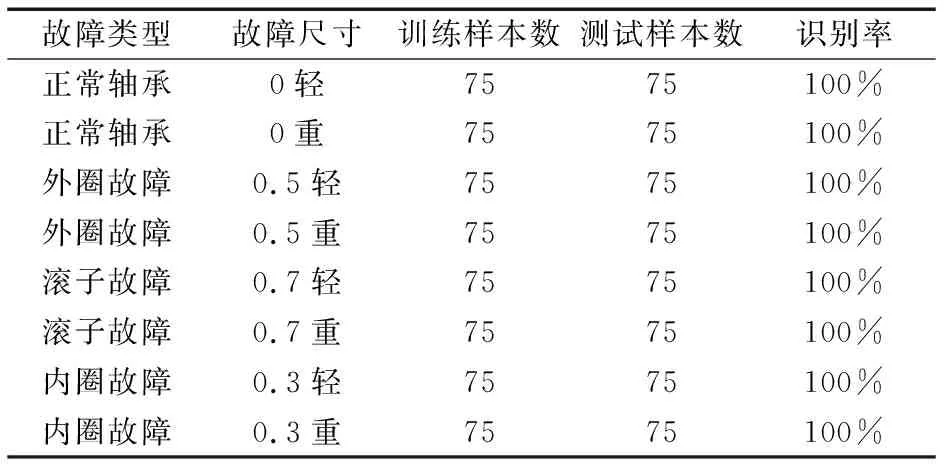
表4 IMF-PE在PSOSVM中的故障识别结果

为进一步验证IMF-PE+PSOSVM在轴承故障诊断方面的有效性，采用常见分类器对IMF-PE特征矩阵进行分类识别(表5)，并提取不同特征矩阵或参数输入PSOSVM进行分类识别(表6)。由识别率可知：1)虽然各分类器对IMF-PE的识别率都达到97%以上，但PSOSVM的识别效率最佳；2)传统的特征参数可以在一定程度上反映轴承的故障状态，但IMF-PE特征不仅可以减少故障状态的误判率，还可以提高模式识别的精度；3)CEEMDAN得到的IMF包含了原始信号的局部特征和不同特征的时间尺度信息，同时避免了模态混叠和虚假模态对特征提取的影响，PE则对时间序列高度敏感，可以突出表征不同工况下的故障状态，IMF-PE值可以揭示信号更多的隐藏特征。综上，说明IMF-PE与PSOSVM联合的特征提取方法非常有助于识别振动信号里隐藏的故障类型和故障严重程度，在滚动轴承故障诊断方面有着非常出色的表现。

表5 不同分类器的识别结果

表6 多种特征参数对故障类型的识别结果

5 结束语

提出了一种将CEEMDAN和PE相结合的故障诊断方法，利用CEEMDAN降低了振动信号分解过程中模态混叠和虚假模态对特征提取的影响，同时，用PE作为特征参数有利于区分滚动轴承故障类型与故障严重程度。该方法具有算法简单，易于实现的优点，可根据分类信息准确、有效地提取隐藏的故障特征信息，分类识别精度较高。在随后的研究中，将进一步简化算法，同时引入实时检测的相关机制和算法，配合更加精准的试验，实现实时故障诊断系统。