关于牵连物体的解题思路探析

(安徽省滁州中学，安徽 滁州 239000)

牵连物体间的位移、速度、加速度关系是高考、竞赛的高频考点，既涉及运动的合成与分解，又涉及系统的机械能守恒。物体间牵连关系在时间上的积累可表现为位移的联系，通过构建显性的位移关系推演隐性的速度、加速度关系，可以提升学习效率，巧妙地运用微元思想可达到化繁为简、化曲为直、化变为恒的目的。本文分别以轻绳(细线)、接触面、轻杆作为牵连物构建物体间的位移关系，解题中运用微元、放大的方法，可以在较短时间构建牵连物体间的制约关系，进一步求解速度和加速度。

1 物体间的牵连物为轻绳(细线)

例1：如图1所示，人在高为h的台阶上用轻绳经滑轮拉小车。若绳的速率恒为v，当绳与地面夹角为θ时，试求此时小车的速率u及加速度a。

图1

图2

解：利用放大的方法构建小车经过极短时间Δt从A点运动到B点的运动示意图(如图2)，在OA上选取OC=OB，根据微元思想ΔABC为直角三角形，小车的合位移AB按照运动效果分解为：(1)AC代表到O点距离减小的效果；(2)BC代表相对O点转动的效果。

评析：分解对象的选择、分解方法的确定是学生解题过程中的难点和易错点，通过放大的方法结合微元思想，学生能确定小车的位移为分解对象，并选择分解到沿绳方向和垂直绳方向。可以采用类似的方法构建小车的加速度和相对O点的向心加速度之间的关系，本文统一用求导的方法。

例2：如图3所示，两根间距为l的光滑细直杆AA1和BB1，固定在天花板上，将绳的一端拴在B点，另一端拴在套于AA1杆子上的珠子D上，另有一珠子C穿过绳及杆BB1、以速率v1匀速下落，而珠子D以一定速度沿杆上升。当图3中角度为α时，珠子D上升的速率v2及加速度a分别为多大？

图3

图4

评析：该题解题方法与例1一脉相承，基于绳不可伸长，构建经过极短时间Δt两珠子之间的位移关系，把复杂的速度、加速度关系转化为显性的位移关系，学生从心理上容易接受，操作起来容易上手，该题加速度的表达形式与例题1有异曲同工之妙。

2 物体间的牵连物为接触面

例3：如图5所示，有一个沿水平方向以加速度a作匀加速直线运动的半径为R的半圆柱体，半圆柱面上搁着一个只能沿竖直方向运动的竖直杆。当半圆柱体速度为v时，杆同半圆柱体接触点和柱心的连线与竖直方向的夹角为θ，求这时竖直杆的速度和加速度分别为多大。

图5

图6

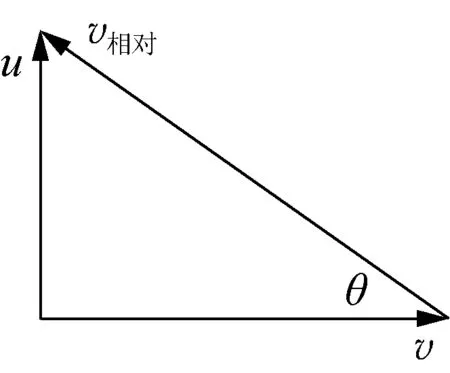
图7

评析：相互接触的坚硬物体在垂直于接触面的方向上的速度大小相等，可以采用运动的合成与分解方法，把物体的速度分解到沿接触面的法线方向和沿接触面的切线方向，利用法线方向的速度相等构建物体间的牵连关系，切线方向的速度为相对速度。本题采用化隐性的速度、加速度关系为显性的位移关系，学生更加容易找到解题思路和突破口，缺点是对数学的要求较高，求解加速度时需要明了半圆柱体也具有加速度。

3 物体间的牵连物为轻杆

例4：如图8所示，细杆OL绕O点以匀角速度ω转动，并推动小环C在固定的钢丝AB上滑动，其中O点到钢丝AB距离为h，试求当图8中夹角为θ时小环的速度和加速度。

图8

图9

评析：对于杆系交叉点的速度求解可以采用运动的合成与分解原理，把杆上C点的运动分解到沿OL方向和沿钢丝AB方向，学生常采用机械记忆的方法，很难把握这种分解的实质。选择位移作为突破口，思路清晰、线索明确，同时可从本质上理解位移、速度、加速度之间的内在联系。

4 结语

求解牵连物体间的位移、速度、加速度之间的关系时既可以利用运动的合成与分解，也可以利用绝对速度等于相对速度加牵连速度的关系，同时也可以通过构建显性的位移关系，再推演隐性的速度、加速度关系。方法没有优劣之分，只有适合与否。