一种大跨径“人字形”三角钢桁架桥的设计与计算

周昱

（广州市市政工程设计研究总院有限公司，广东 广州 510600）

1 工程概况

司马坡岛位于海南省省会海口市中心城区东部的南渡江上，是南渡江河口段的江心岛，岛的西侧是南渡江西岸生活片区的城市主干道滨江路。基于项目优越的地理位置、岛中岛的生态和景观格局，司马坡岛将建成一座包含国际级体育赛事场地、顶级度假设施、多元旅游活动的岛中岛。司马坡大桥为连接小岛与其西侧城市主干路的唯一通道。根据总体布置，桥梁位于一“右进右出”的T字形路口上；考虑到司马坡岛的功能定位，本桥具有很高的景观性要求，建成后应作为当地的地标性建筑，见图1。

2 设计简介

司马坡大桥为一单跨165m，空间上呈三脚架造型的半穿式钢桁架桥。上部结构主体为钢桁梁，主梁外轮廓包裹钛合金装饰板，见图2。桥梁上部结构由两片高18m，斜向布置三角形桁架构成，其平面呈“人字形”分肢，见图3。桥设置双向两车道及人行道，岛屿侧（未分肢侧）路面宽10.5m；城市侧（分肢侧）路面宽7.25m。

图3 典型横断面

钢桁主梁由两种四片内倾的桁架交于一点构成。主梁在空间上整体呈一个等腰三角架造型，桁高最高处即为主梁四片桁架交点。主桁梁两分肢段夹角为60°，分肢段与未分肢段下弦杆的交角为153°。

立面上桁架采用变高桁架，呈三角形造型。每片桁架节间长度相等为8.88m，均采用N形桁架。横断面上，主梁未分肢段两片桁架一内倾，构成三角形断面；桥面支撑于横梁上，横梁与下弦杆连接。主梁分肢段横梁半悬臂连接到桁架二上，构成一个”L“形断面。此段横梁与主桁架二的竖杆共面，构成一系列大小不一的”L“形钢架，这些钢架则通过弦杆和边纵梁连接起来，共同构成主梁分岔段的两分肢。钢桁架主要构件见图4。

图4 桥梁主要构件示意

主桥的上、下弦杆采用平弦四边形截面，与桁架内倾角度一致。竖杆，斜腹杆，边纵梁构件采用箱型断面。平纵联，中纵梁，一般横梁采用H型断面（见图5）。其中弦杆采用Q460qD钢材，其余构件采用Q420qD钢材。桥梁采用整体式全焊节点，即每段上、下弦杆即为一预制节点。平纵联连接中纵梁与下弦杆节点，采用N行布置。桥面采用正交异性板桥面，采用U形加劲肋。

3 静力计算

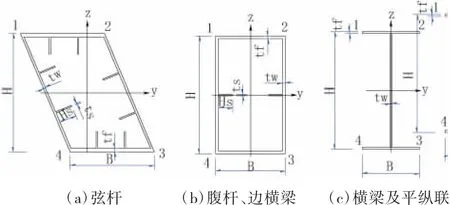
图5 主要构件断面示意

采用空间杆系模型建立全桥有限元模型，对全桥主要构件进行静力分析。计算考虑结构恒载（包括一期、二期）、活载（城A、人群荷载及温度效应）、百年静风荷载和E2地震荷载。其中风荷载结构风压由全桥风洞实验测得；地震荷载采用反应谱分析地震加速度值为0.30g，地震动反应谱特征周期为0.35 s。经计算有以下三个控制工况，工况Ⅰ：标准组合；工况Ⅱ：工况Ⅰ+静风荷载；工况Ⅵ：恒载+地震力。计算分析模型见图6。

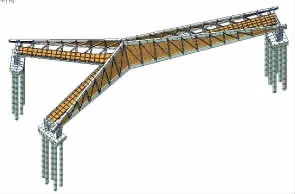
图6 计算分析模型

3.1 内力结果分析

表1 中给出了主梁各构件的最大内力值，其中弦杆对应图4中的3～6构件、腹杆对应7～8构件、中纵梁对应12构件、边纵梁对应9构件、横梁对应10构件。

由计算结果可以看出上、下弦杆为主要受力构件，轴力为控制内力；同时由于结构呈空间异型结构，弦杆亦承受较大的面内和面外弯矩。由图 7（a）～（c）可见，主桁构件所产生的拉压应力分布趋势是有一致性的。上弦杆和斜腹杆承受压应力，下弦杆和竖腹杆承受拉应力，这种受力体系是合理的。上弦杆越靠近支座，压力越大；下弦杆越靠近支座，拉力越大。这是由于立面为三角形桁架，桁高逐渐变小故弦杆轴力相应增大。弦杆的弯矩分布也呈现同样趋势，这由于桁架端部为一大节点，刚度较大导致次弯矩集中所致。

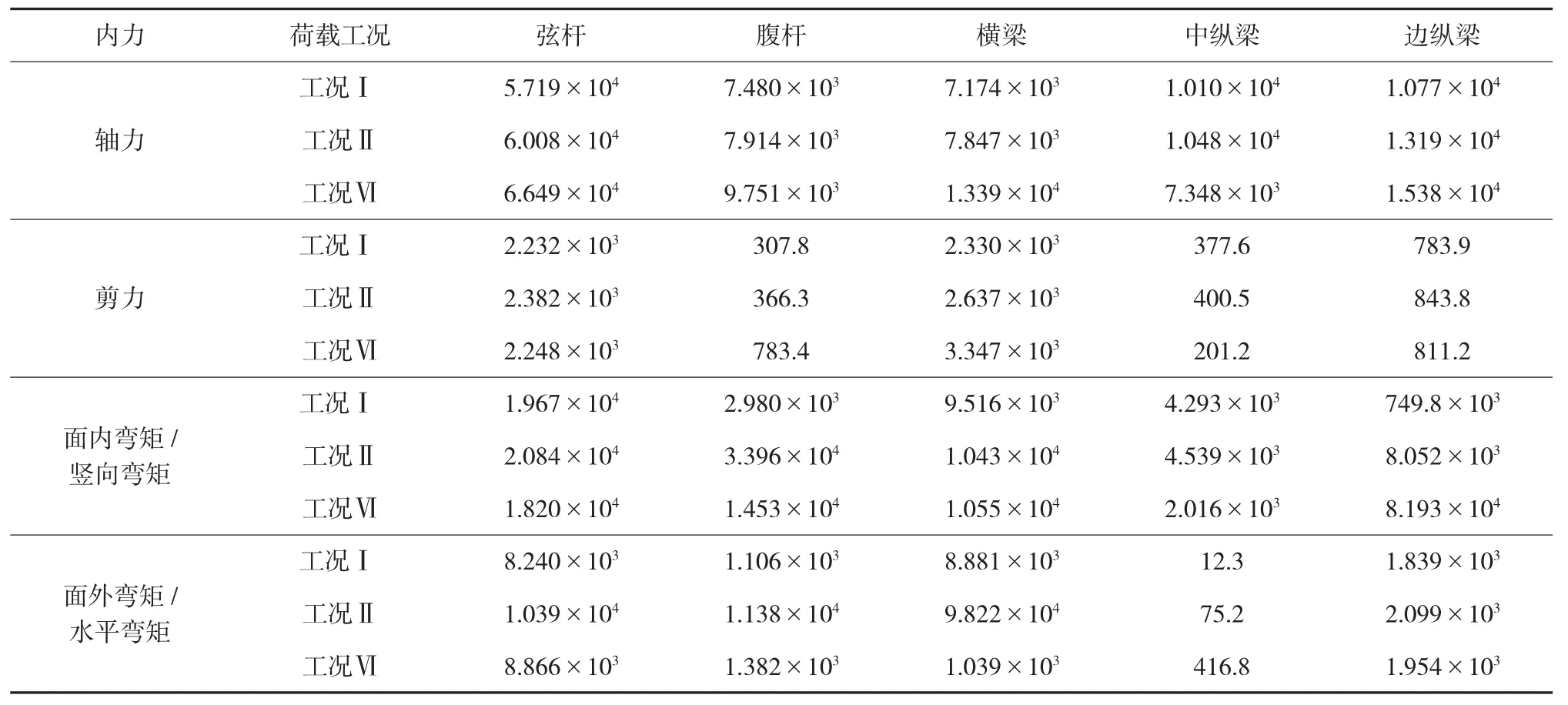
表1 主要构件最大轴力值kN·m

图7 主要构件内力分布图（工况Ⅰ）

由表1中结果可以看出，同弦杆一样，腹杆亦主要承受轴向荷载；同样值得注意的是腹杆端部承受较大的面内和面外弯矩，且面内弯矩约为面外弯矩的3倍。这是由于桁架采用整体全焊式节点，节点刚度大导致面内次弯矩较大；同时由于桁架为空间结构，其横向效应致使腹杆承受一定的面外弯矩。基于此受力特点，腹杆均设计成箱型截面以增加构件抗弯承载力及面内面外稳定性。

图 7（d）～（f）给出了横梁内力分布，位于桁架分肢及支点处的横梁平衡内倾桁架的水平推力，承受较大的轴向力；其余横梁均为竖向受弯构件。由图7（e）可见未分肢侧横梁受力近似于简支梁，分肢侧横梁受力近似于悬臂梁，这与其主桁架结构特点也是相匹配的。支点处的水平力主要由支点横梁承担，故此处承受较大的面外弯矩荷载，故此处横梁进行加强，采用箱型断面以提高其水平抗弯能力。

中纵梁及边纵梁作为板桁桥面体系的一部分，起部分下弦杆的作用；图 7（g）、（h）中纵梁的轴力分布也印证了这一点，其内力大小分布规律与下弦杆类似。同时由于边纵梁位于L形分肢端部，亦分担分肢部分主梁弯矩，其竖向弯矩值明显大于中纵梁且其内力分布情况亦与其结构构造相匹配；即可看作支撑在边支座及主梁分肢位置的近似简支梁。另外由表1可见，由于结构的空间异形特性，边纵梁还承担较大的水平弯矩荷载。

3.2 构件应力计算结果

根据上述桥梁受力特点，对不同构件采用相应的截面。桥梁采用容许应力法设计，容许应力值根据板厚折减及受压构件稳定性进行折减。图8给出了构件在工况1下的正应力包络图，表2给出了主要构件各工况的组合应力值（考虑次应力相应）。可见上弦杆的控制工况为工况Ⅰ，最大压应力值210 MPa；下弦杆的控制工况为工况Ⅱ，最大拉应力值340 MPa；腹杆、横梁以及边、中纵梁的控制工况均为工况Ⅰ，最大组合应力值分别为204MPa、178MPa、209MPa。经验算构件应力值均小于容许应力，强度满足规范要求。

图8 主要构件应力图（工况Ⅰ）

表2 主要构件最大应力值MPa

3.3 位移计算结果

恒载作用下最大挠度发生在上弦杆中部，即由分叉口到小岛组成跨的“跨中”位置处。挠度的最大值为495mm。活载作用下最大挠度发生在边纵梁中部区域，即由分叉口到城市侧组成跨的“跨中”位置处。最大活载位移值为75 mm＜L/800=193mm满足规范要求，见图9。

图9 主要构件应力图（工况Ⅰ）

4 全桥屈曲分析

对全桥进行弹性稳定性分析，分析理论是假设结构在失稳时，处于弹性变形阶段，结构内力与外荷载成比例关系，求解过程是把结构的稳定分析转化为数学上特征值问题。在有限元程序计算中，特征值方程的矩阵形式如下：

式中：[K0]为线弹性刚度矩阵；[Kσ]为参考荷载作用下的几何刚度矩阵；λ为荷载安全系数。

在有限元计算程序中，求解极限荷载需要进行荷载—位移全过程分析，问题在数学上可归结为求解非线性平衡方程：

对司马坡大桥在关键工况下的极限承载力进行分析计算，分析方法采用弹性稳定分析。计算中考虑的荷载为：恒载、车辆及人行活载、风荷载。进行屈曲模态分析后，提取前2阶屈曲模态见图10。计算结果可见，第1阶失稳模态临界荷载系数为49.8，失稳模态为上弦杆侧向失稳；第2阶失稳模态临界荷载系数为59.6，失稳模态为上弦杆侧向失稳+分肢侧边纵梁竖向失稳。可见由于本桥整体呈一类似于三脚架的构造形式，结构稳定系数较高，桥梁稳定性较好。同时前两阶失稳模态都是主桁侧弯导致杆件的失稳，即相对竖向刚度，结构的横向刚度较小。

图10 前两阶屈曲模态

5 动力特性分析

采用L a nc z o s法对桥梁进行动力特性分析，提取前四阶振型见图11。第一阶振型为一阶正对称侧弯，频率0.80 H z；第二阶振型振型为一阶正对称竖弯，频率0.81 H z；第三阶振型为一阶反对称竖弯，频率1.48 H z；第四阶振型振型为二阶正对称侧弯，频率 1.71 H z。

图11 前4阶振型

该桥一阶振型和二阶振型的自振周期较长，体现了大跨度钢桁架桥整体较柔，结构轻巧这一特性，这对于结构抗震是有利的。另外值得注意的是，第一、二阶振型频率较为接近，即桥梁存在一定的侧弯、竖弯耦合的动力特征。

6 结语

随着我国城市桥梁建设的快速发展，人们对桥梁的景观造型要求越来越高。钢桥因为架设速度快，造型美观多样，常常会成为城市当中一道亮丽的风景线，在城市桥型中很有竞争力。本文结合司马坡大桥工程，介绍了一种新式的“人字形”三角钢桁架桥；并对该桥进行了动、静力分析计算，得到以下结论：

（1）该桥为空间异性结构，其空间受力效应明显，桁架杆件承受较大面外力。故多采用箱型截面构件以提高面外/水平抗弯能力。

（2）由于采用了全焊式整体节点，节点刚度大，桁架杆件面内次弯矩大。弦杆弯曲应力（次弯矩及横向弯矩）约占总设计应力的30%左右，腹杆则达到40%以上。

（3）三角形桁架的主要受力构件为弦杆，上弦杆承受压力，下弦杆承受拉力。由于桥梁立面为三角形结构，越靠近支座桁高越小，弦杆受力也越大。

（4）该种结构整体稳定性良好，结构较为轻巧抗震性较好；且桥梁造型较为独特，具备一定的景观效果，可作为城市景观桥梁的一种桥型方案。