大跨径高墩连续刚构桥地震反应分析

蔡建业

(中铁第四勘察设计院集团有限公司，湖北武汉 430063)

1 工程概况

该高墩大跨连续刚构桥主桥全长1 140 m，跨径布置为(130+4×220+130) m，主梁横截面为单箱单室变截面，采用C55混凝土悬臂浇注，端支座与主梁跨中处梁高4.5 m，根部箱梁高度12 m，梁高按二次抛物线变化。

主墩采用双肢薄壁与单肢薄壁组合形式：主墩上部为空心竖直双肢薄壁墩，空心薄壁厚度横桥向厚1 m，顺桥向厚0.6 m，高度均为60 m；下部为箱形截面单肢薄壁墩，采用C50混凝土爬模施工，墩柱顺桥向采用1∶60坡率放大，横桥向按1∶40坡率放大，高度分别为81.49 m、165.74 m、248.22 m、239.38 m、18.27 m。桩基础由25根桩径为3 m群桩组成，长度为40 m，桩底嵌入岩石。主桥立面布置如图1所示。

图1 主桥立面布置(单位：cm)

2 自振特性分析

2.1 有限元模型建立

结构力学模型是进行结构静、动力分析时所采用能够反映结构力学性能和构造特点的计算图式。本文在建立结构模型时主要有以下几点考虑[1-2]：

(1)模型中各个部分采用的单元类型以及结构节点单元的划分，一定要尽量符合实际结构的构造特点和受力特点。

(2)结构内部各个独立部分之间的连接，一定要符合实际情况。

(3)整个结构体系的边界条件，一定要尽可能地准确，接近真实情况。

(4)模型的建立还要充分考虑所要研究的内容，抓住主要矛盾，舍弃次要和无关的部分。

遵循这一宗旨，使用有限元软件建立考虑桩—土—结构相互作用的全桥模型。建模时，主梁、桥墩、承台、桩均采用空间梁单元模拟；桩与土之间相互作用采用等代土弹簧单元模拟；桥梁支座作用通过耦合作用实现。模型的约束条件如下：主梁与边墩的连接，对于支座不可移动的自由度，取为主从，可移动的自由度放松；桥墩在承台顶嵌固；桩顶嵌固于承台底；桩底固结。

在模型当中，对于二期恒载、桩—土相互作用[3]分别按照以下方式考虑：

①结构二期恒载转化为等效密度添加到主梁的密度上。

②桩土的相互作用，根据地震安评报告共分为5个土层，各土层的水平地基比例系数m值按相关规范取值，再按质弹阻模型[4-5]计算桩—土相互作用中土弹簧模量和二力杆的面积，见表1。

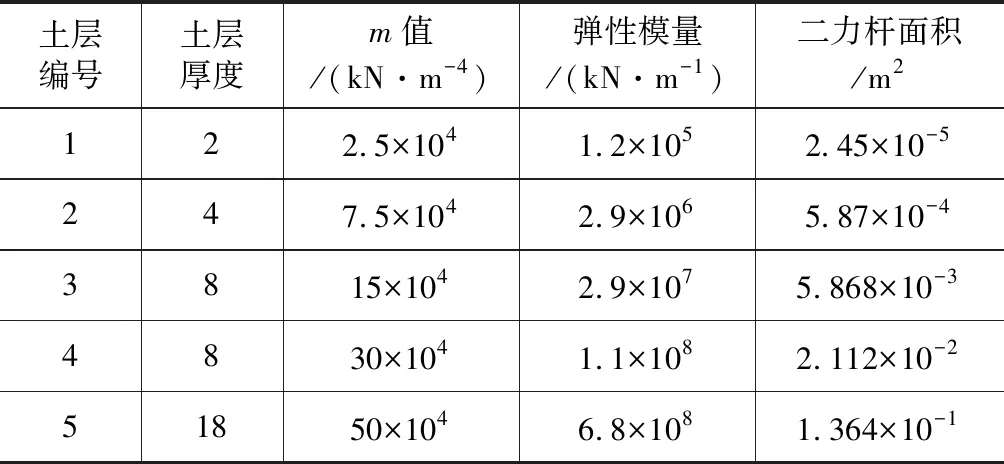
表1 土弹簧的刚度和二力杆的面积汇总

2.2 桥梁结构动力特性分析结果

根据上述有限元模型，采用空间迭代法对该桥进行动力特性分析，分析结果表明：前十阶振型主墩的纵向和横向振型相差较大，以主墩横向振型优先；由于桩—土—结构相互作用，桥梁结构变柔，整体刚度下降，自振周期延长。表2列出了模型前十阶频率和相关的振型特点。

3 地震反应谱分析

表2 桥梁结构动力特性

3.1 反应谱概念[6]

反应谱法用于抗震计算包括三个基本步骤：第一步是获得地震动反应谱；第二步是将结构振动方程进行振型分解，将物理位移用振型广义坐标表示，而广义坐标的最大值由第一步中所得反应谱求得；第三步是反应量的最大值可通过适当的方法将各振型反应最大值进行线性叠加，得出这项反应的最大值。因此，反应谱理论是建立在以下基本假定的基础上：

(1)结构的地震反应是线弹性的，可以采用叠加原理进行振型组合。

(2)结构物所有支撑处的地震动完全相同。

(3)结构物最不利地震反应为其最大地震反应。

(4)地震动的过程是平稳随机过程。

以上假设，第1、2项实际上是振型叠加法的基本要求，第3项是需要采用反应谱分析的前提，第4项是振型分解理论的自身要求。

3.2 反应谱基本原理

利用单质点体系，由于地面运动位移δg(t)引起的单质点振子的地震振动方程为：

则单质点振子的地震相对位移反应的杜哈美(Dumhamal)积分式为：

由于地震加速度是不规则的时间函数，一般可以采用数值积分法求出反应的时间变化规律，即反应时程曲线。对不同单质点体系(不同的圆频率或不同周期，不同的阻尼比)在选定的地震加速度输入下，可获得一系列的相对位移、相对速度和绝对加速度的反应时程曲线，并可以从中找到它的最大值。以不同单质点体系的周期为横坐标，以不同阻尼比为参数，就能绘出相对位移、相对速度和绝对加速度的最大值的谱曲线，简称反应谱。

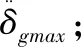
3.3 反应谱理论的地震力计算

(1)单质点体系的最大地震力计算。

对于单质点体系，其最大地震力为：

在桥梁抗震设计规范中，还引入综合影响系数Cz，以考虑结构的延性耗能作用，则P=CzKhβW。

(2)多质点体系的最大地震力计算。

采用有限元法，可以得到多质点体系的地震振动方程

对于这一联方程组，可利用振型分解法分解成一系列相互独立的振动方程，于是将多质点体系的复杂振动分解为各个振型的独立振动，从而可以采用单质点体系的反应谱理论来计算各振型的最大反应。最后，将各个振型的最大反应按合适的方法相组合，即可得到多质点体系的各项反应值。

钩藤猝倒病可用3亿CFU/克哈茨木霉菌20～50倍，或10亿个/克枯草芽孢杆菌800～1 000倍，或8%井冈霉素A水剂100～125倍，或10%苯醚甲环唑1 000～2 000倍，或43%戊唑醇悬浮剂WG 2 500～4 000倍，或1%申嗪霉素悬浮剂800～1 000倍喷雾防治，在苗床或育苗盘出现初始发病中心时及时普防。

3.4 计算原则及基本参数

利用前述结构动力特性计算结果，采用反应谱方法对成桥状态结构进行地震反应分析[7]。桥梁抗震分析中其无量纲振型参与系数的总合应大于0.95，故本桥参与计算的振型阶数高达300阶时方可满足，因此抗震计算中采用了前300阶振型，结构阻尼比取0.02。

图2 地震输入反应谱

根据该桥《地震安全评估报告》，取100年为设计基准期，采用50年超越概率10 %(简称P1)，对应反应谱加速度最大值为0.116g和100年超越概率3 %(简称P2)，对应反应谱加速度最大值为0.26g(g为重力加速度)两种概率水准下的地震作用作为结构的地震输入反应谱如图2所示。地震输入方式采用两种工况：(1)顺桥向+竖向；(2)横桥向+竖向，竖向地震系数取水平地震系数的2/3。

3.5 计算结果

根据前文所述，P1地震概率作用下的内力反应用于验算结构强度，P2地震概率作用下的位移反应用于验算结构的变形。P1地震概率作用下墩底截面的内力响应值详见表3。P2地震概率作用下全桥位移云图值详见图3、图4。

综合两种工况分析结果可知：

(1)大跨径连续刚构桥在地震作用下主梁的最大内力反应值一般在中、边跨跨中或主梁根部截面处，墩身内力反应最大值一般发生在墩顶或墩底截面处，最大位移值一般发生在桥墩顶部或主梁上。

(2)墩越高其墩底内力值也越大，最大顺桥向弯矩4.72×105kN·m出现在8号墩底，最大横向弯矩5.76×105kN·m出现在7号墩底。

表3 墩底内力计算结果

图3 横桥向全桥位移图(单位：m)

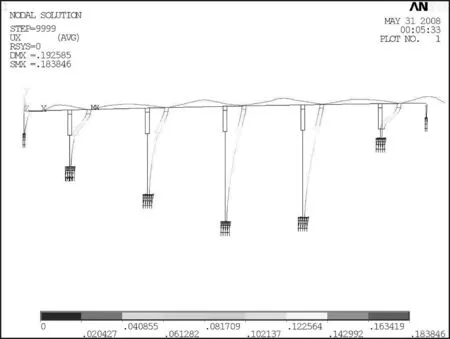
图4 顺桥向全桥位移(单位：m)

(3)墩顶顺桥向位移具有一定的协调性，各墩顶顺桥向最大值相差不大，最大值192.6 mm出现在5号墩顶。墩顶横向位移值与墩高成正比，最大值出现在7号墩墩顶，值为308.9 mm。

(4)梁的竖向位移最大值出现在7号、8号两最高墩之间，梁的横向位移最大值出现在7号墩位置处。

4 结论

通过建立有限元模型，对某高墩大跨连续刚构桥进行了结构动力特性分析，并考虑桩—土相互作用对桥梁进行反应谱地震计算，得出以下几点结论：

(1)考虑桩—土—结构相互作用，桥梁结构变柔，整体刚度下降，自振周期延长，说明土层中的桩—土相互作用对上部结构的动力特性影响较大。

(2)计算结果显示：墩的内力值随着墩高的增加而增加，墩顶位移值也有相应的规律，墩顶的位移最大值出现在最高墩顶，梁的横向位移和竖向位移最大值出现在两高墩之间。

(3)连续刚构桥的位移以水平位移为主，竖向位移相对较小，水平位移中沿横桥向的位移最大，顺桥向的次之。

(4)连续刚构桥，地震的作用效果主要体现在桥墩的底部和顶部，墩身内力反应最大值发生在墩底界面处，此截面是墩体最危险截面。