框架锚索边坡支护结构的离心机模型试验研究

林 顺， 向 波, 蒋瑜阳, 王晓文

(四川省公路规划勘察设计研究院有限公司, 四川成都 610041)

[通信作者]向波(1973～)，男，博士，高级工程师，主要从事岩土工程方面的勘察设计与研究工作。

我国正处于基础设施建设蓬勃发展的关键时期,大量的公路工程新建在地形条件严峻、地质构造复杂、边坡灾害类型多样的山区，因此沿线边坡工程的安全性对保障工程建设的顺利进行以及今后线路的正常运营具有重要意义[1-2]。

框架锚索是通过对固定于稳定岩层中的锚索施加张拉力，利用框架梁将力均匀分布在坡面上，从而形成一种主动受力的边坡支护结构。随着锚索技术和防护工艺的日趋完善，已广泛应用于公路、铁路、矿山、水电等岩土工程中[3-5]。虽然关于框架锚索支护结构的加固设计和内力计算已有较多的研究成果[6-8]，但是这些传统的计算方法假设条件较多，存在一定的局限性，且缺少模型试验为基础进行验证。现场监测试验虽然能得到真实应力状态下框架锚索的工作性能和状态，真实性和准确性较高，但是所需试验费用较高，时间较长，随机性较大，不便开展重复试验。土工离心机试验通过离心加速度作用可以将按尺寸缩放的试验模型还原到真实的应力状态，可在模型内部灵活布置各种传感器，开展多种工况下的可重复模型试验，有助于我们更加直观、系统地研究边坡支护或支挡结构的工作机理，各部件的受力状态。赵偲聪[9]、张泽林等[10]、周健等[11]、李祥龙等[12]基于离心机模型试验研究了不同类型边坡的宏观变形模式和支护结构的力学性状。离心机模型试验作为一种较新的试验手段，鲜有关于框架锚索加固边坡的离心机试验研究。

目前，对于框架锚索支护结构的设计施工还主要依赖经验，缺乏较为系统的理论基础，对框架梁的受力状态以及框架梁下边坡土体反压力的分布特征尚不明确。基于此，本文设计了3种不同岩性结构组合的边坡，通过离心机试验研究框架锚索支护体系加固不同岩性结构边坡时的受力特征及框架锚索-边坡的相互作用。

1 土工离心机模型试验

1.1 试验设备

试验在西南交通大学岩土工程研究所土工离心机试验室进行，该实验室采用TLJ-2型离心机，最大离心加速度200g，最小离心加速度10g·t，最大容量100g，有效半径2.7 m，最大半径3 m。包含两个模型箱，其中大型模型箱内部净空0.8 m×0.6 m×0.6 m(长×宽×高)，大型模型箱内部净空0.6 m×0.4 m×0.4 m(长×宽×高)，离心机设备如图1所示。

图1 土工离心机设备

1.2 相似关系设计

根据相似三定律，以几何尺寸、离心加速度和密度为主控量，推导出其余物理量的相似常数(表1)。首先确定几何相似常数(n=Hp/Hm，Hp为原型边坡高度，Hm为模型边坡高度)，然后根据几何相似常数计算离心模型试验加载加速度以及加载的荷载容量，与约束条件(包括模型边坡高度、最大离心加速度、最大载荷重量)进行比较，如果不满足需调整几何相似常数n，直到满足条件为止。

1.3 模型制作及加载工况

为研究框架锚索结构加固不同岩性结构边坡时的力学性状和变形机理，设计了3种不同的边坡结构，分别为框架锚

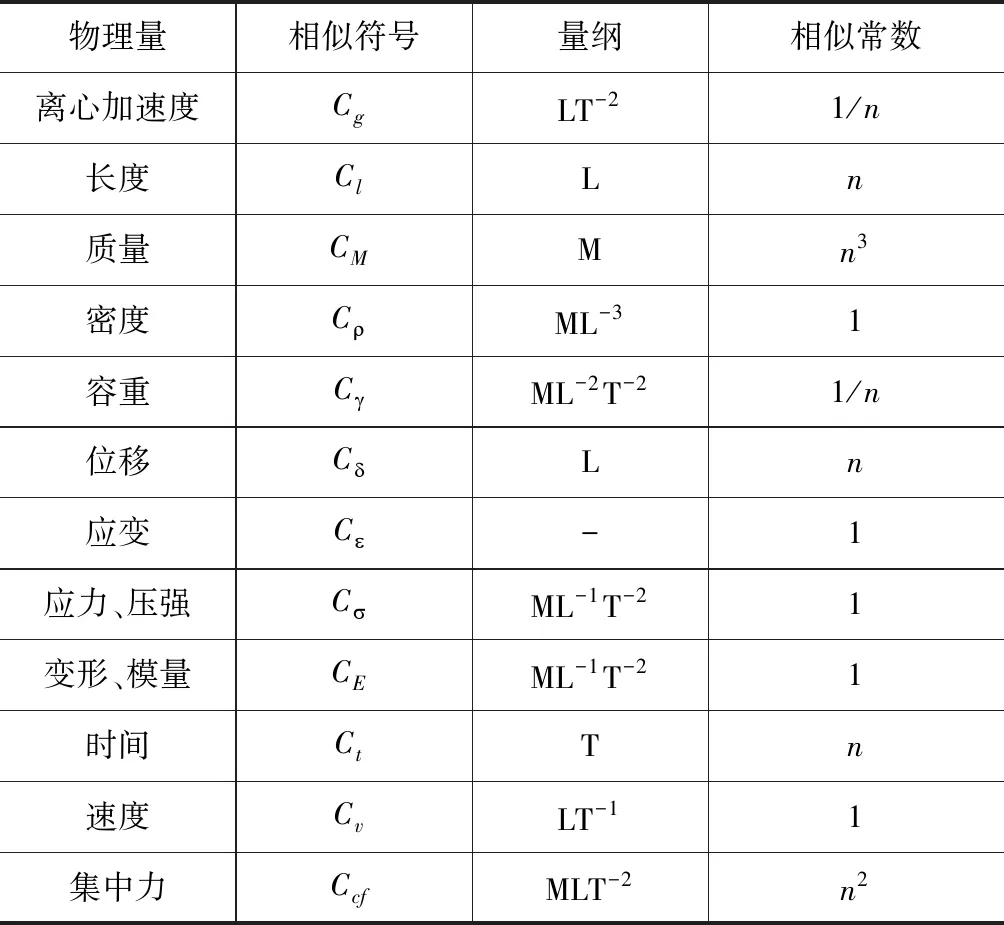
表1 离心机试验物理量相似关系

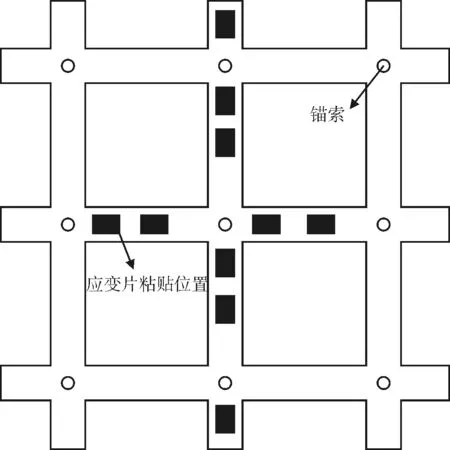
索加固直线滑动型岩质边坡(上风化岩-下基岩)、框架锚索加固基覆层边坡(上覆土-下基岩)以及框架锚索加固均质土坡。3个边坡模型几何相似常数及外部尺寸均相同，即n=50，左侧高度15 cm，坡高20 cm，底部长80 cm，横向宽60 cm，上部滑动层长20 cm，坡率1∶0.75。在模型箱底部浇筑混凝土模拟基岩，直线滑动型岩质边坡的上风化层材料采用河沙、石膏粉、黏土和水按7.5∶2∶2∶0.9质量比配置而成，基覆边坡的上覆土采用河沙、黏土和水混合搅拌均匀制成，在滑动面上铺设塑料薄膜并涂抹凡士林以模型上下岩土体之间的相对滑动。均质土坡的材料采用河沙、黏土和水按1.5∶1∶0.35质量比配置而成。采用直径为5 mm的细圆形钢筋模拟锚索，锚固段位于基岩内部，长270 mm，自由端位于上部坡体中，长120 mm，锚索张拉段位移坡面处，长30 mm。在锚索的锚固段、自由段均布置应变片，布置方式如图2所示。3个边坡模型的锚索各部分长度及应变片布置方式均相同。框架梁采用厚度为1 mm，外边长为15 mm的不锈钢方管来模拟，并在框架梁的受压侧和受拉侧布置应变片以计算不同截面位置处的弯矩值，如图3所示，在框架梁底部布置

(b)锚索表面粘贴应变片图2 锚索应变片布置

(a)应变片布置示意

土压力计以获取坡体反力的大小。3个边坡的框架梁应变片布置方式均相同，而直线滑动型岩质边坡和基覆边坡的土压力计布置方式相同，均质土坡土压力计不同方式与前两者不同。3个边坡的具体几何尺寸、制作完成的边坡模型以及土压力计布置方式如图4～图6所示。

(a)应变片布置示意

(b)框架梁表面粘贴应变片图3 框架梁应变片布置

离心机试验加载运转加速度范围为20～70g，采用以10g为一个量级的分级加载方式，加载到20g、30g、40g时分别保持稳定状态10 min，加载到50g时保持稳定状态30 min，加载到60g和70g时分别保持稳定运转10 min，直到试验结束，加载过程曲线如图7所示。3种边坡结构的离心机试验分3次试验进行，试验一为框架锚索加固直线滑动型岩质边坡离心机试验，试验二为框架锚索加固基覆层边坡离心机试验，试验三为框架锚索加固均质土坡离心机试验。

2 离心机试验结果分析

2.1 框架梁弯矩

以离心加速度为50g，锚索预应力为400 kN的工况为例分析框架梁的纵梁和横梁弯矩变化，采用材料力学相关公式根据框架梁的抗弯刚度EI将应变转变为弯矩，图8给出了框架梁的纵梁弯矩变化，横坐标表示框架梁纵梁，图中虚线表示与纵梁相交的横梁。图9给出框架梁横梁的弯矩变化，虚线表示与横梁相交的纵梁，规定受拉为正，受压为负。

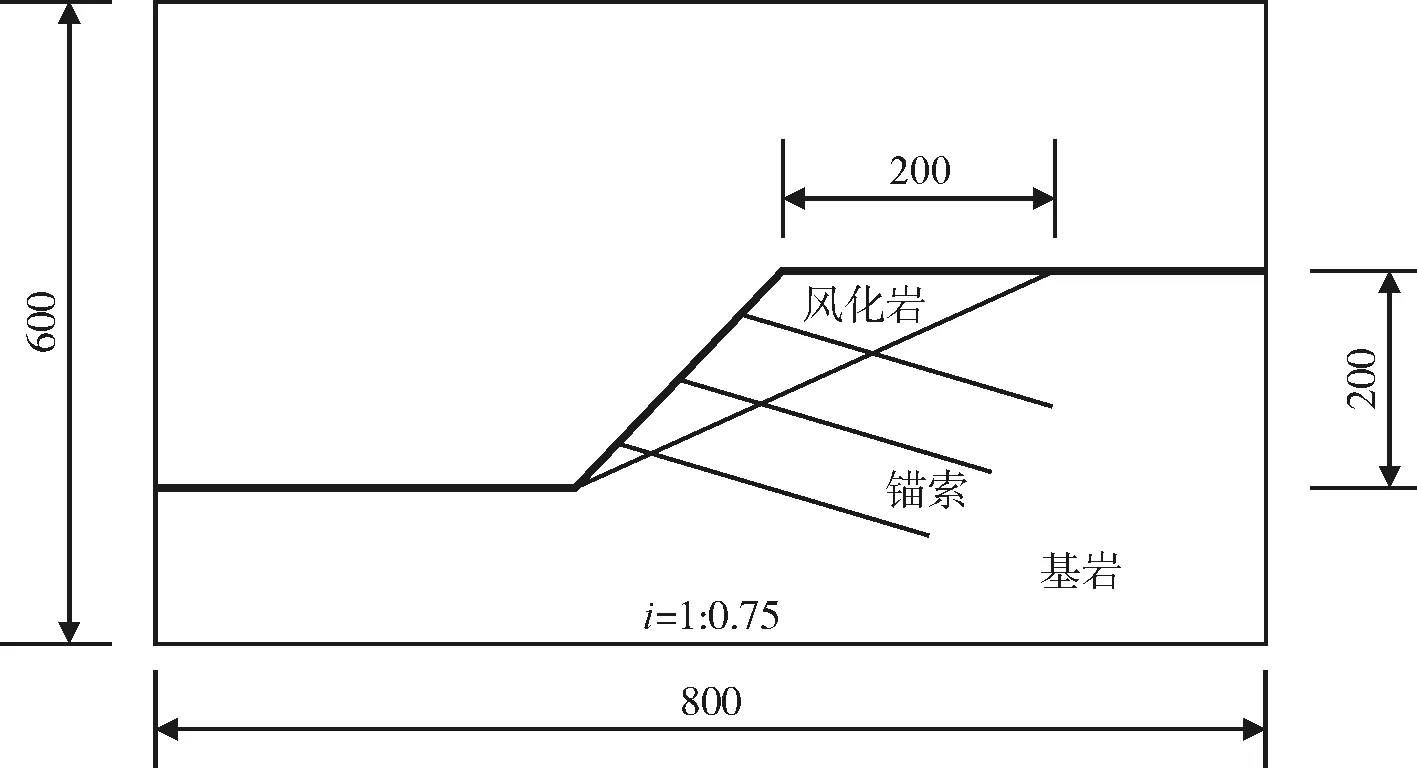
(a)边坡平面尺寸(单位:mm)

(b)制作完成的边坡模型

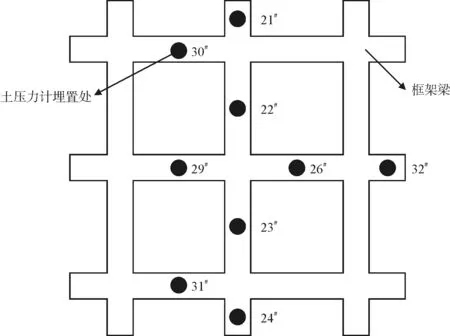
(c)土压力计方式图4 框架锚索加固直线滑动型岩质边坡

从图8纵梁不同位置处的弯矩变化可以看出，三个试验的纵梁在预应力作用点附近均承受正弯矩作用，其中纵梁中部预应力作用点附近所受的正弯矩值较大，上下两个预应力作用点附近所受正弯矩值较小。在纵梁的两个端点位置处弯矩值为零，在两个锚索中间部位处框架梁所受弯矩值为负。整个纵梁呈现出受拉和受压状态交替出现的特征。从图9横梁不同位置处弯矩变化可以看出，在中间预应力作用点附近框架梁承受较大的正弯矩，其余各点均承受负弯矩，横梁也呈现出与纵梁相似的受拉和受压交替出现的特征。在锚索的约束下将框架梁假设为Winkler地基梁作用于坡面上，由于框架梁下边坡岩土体材料物理力学性质不同，所以地基反力系数也不同，因此不同试验的纵、横梁弯矩值有一定的差异性，呈现出离散型变化，框架梁受力状态与其下卧岩土体(地基)的物理力学性质、软硬程度有关。

2.2 框架梁弯矩与锚固力的关系

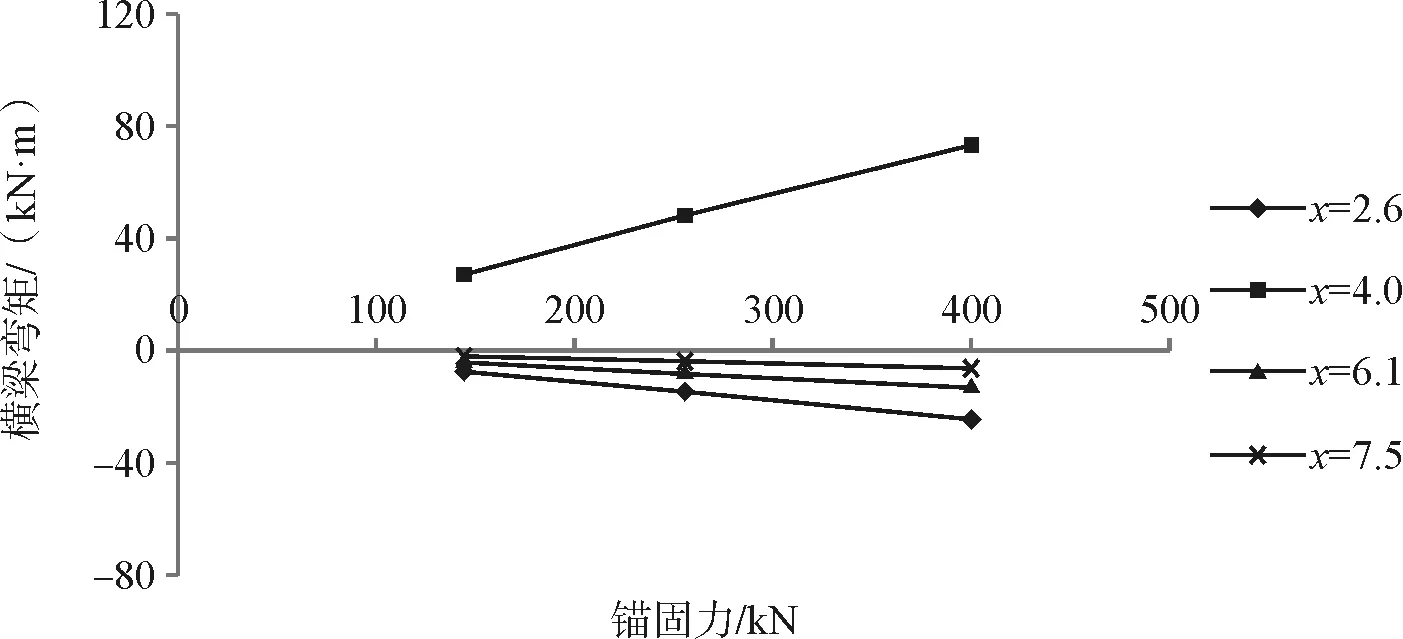
通过改变试验三中锚索张拉段的预应力大小，研究不同预应力下框架梁纵、横的弯矩变化规律。开展144 kN、256 kN及400 kN锚索预应力下的离心机试验，得到框架梁的中间纵梁距顶部不同位置处的弯矩值，及中间横梁距左侧不同位置处的弯矩值，图10为不同锚索预应力作用下，框架梁纵、横梁弯矩的变化曲线。

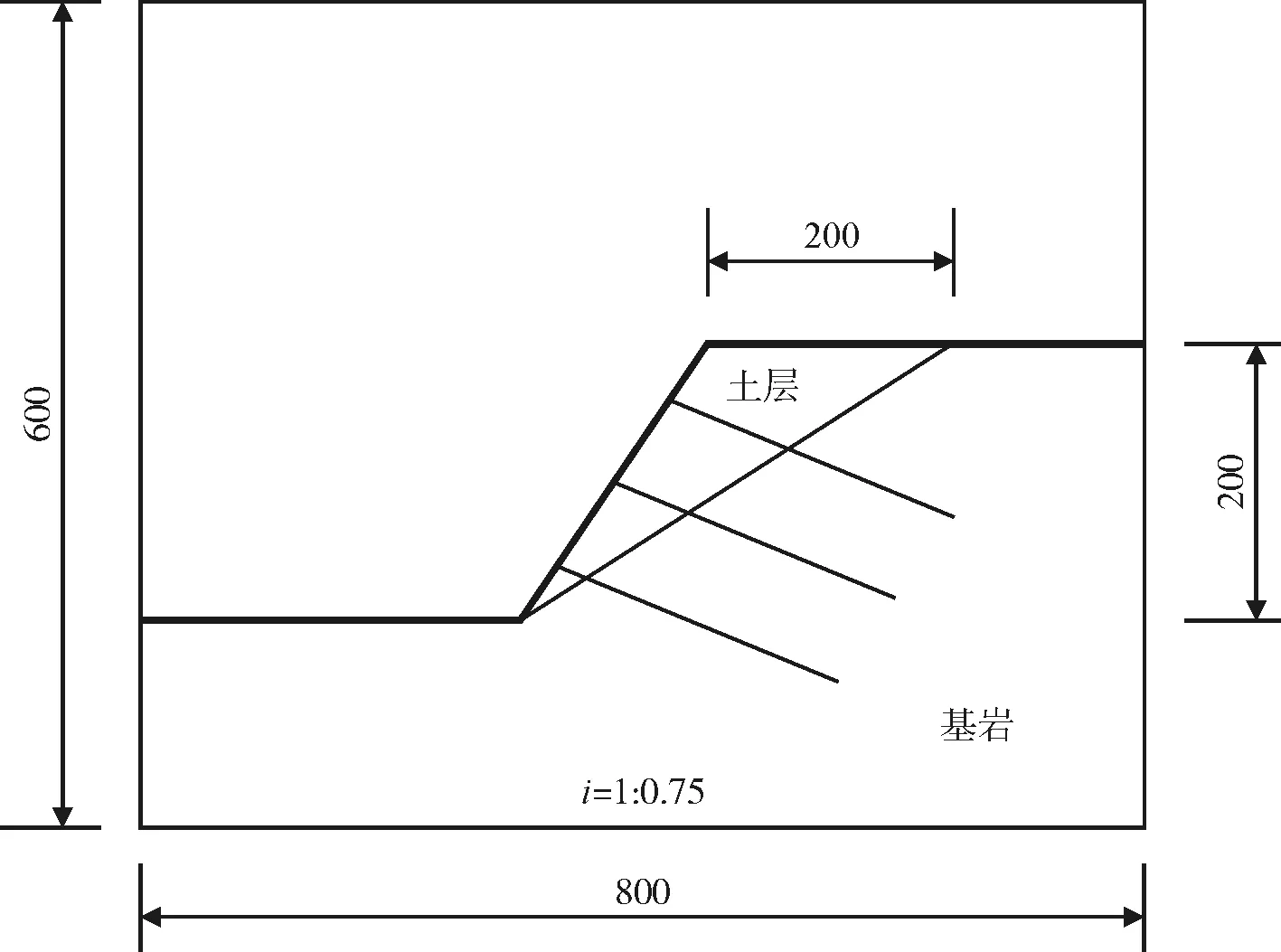
(a)边坡平面尺寸(单位:mm)

(b)制作完成的边坡模型图5 框架锚索加固基覆层边坡

从图中可以看出随着锚索预应力值的增大，纵梁不同位置处的正、负弯矩值均呈现出线性增大的趋势，增大幅度较小。横梁不同位置处的正、负弯矩值随着锚索预应力的增大也呈现出线性增大的趋势，但是增大幅度较为明显，说明横梁对锚固力的变化较为敏感，在确定框架锚索的锚固力时，应综合考虑纵梁和横梁的间距、尺寸以及荷载分担比等因素。

2.3 框架梁下坡体压力分析

图11为离心加速度50g，锚索预应力400 kN工况下，中间纵梁下坡体压力大小分布图，其中横坐标表示与坡面紧贴的中间纵梁，虚线为预应力作用点位置。

从图中可以看出三个试验的最大梁底坡体压力均出现在框架梁中部，在纵梁上下端点附近坡体压力较小。在计算梁底地基反力时应考虑梁底坡体压力的非线性分布，以便于框架梁的结构设计能更接近实际受力状态。由于试验二的梁底坡体材料相比于其他两组试验最软，因此所测得的坡体压力最大。试验一的梁底坡体材料与试验三的相比较硬，地震反力系数较大，所得到的坡体压力也大于试验三的坡体压力。在梁长6～8 m之间，试验一的坡体反力大于试验三的坡体反力，可能是由于坡面平整度或测量误差引起。坡体材料的地基反力系数越大，梁底的坡体压力越小。框架梁底部的坡体压力也与梁底坡体材料的物理力学性质、软硬程度及松散破碎程度有关，在进行框架锚索结构设计时应考虑以上因素。

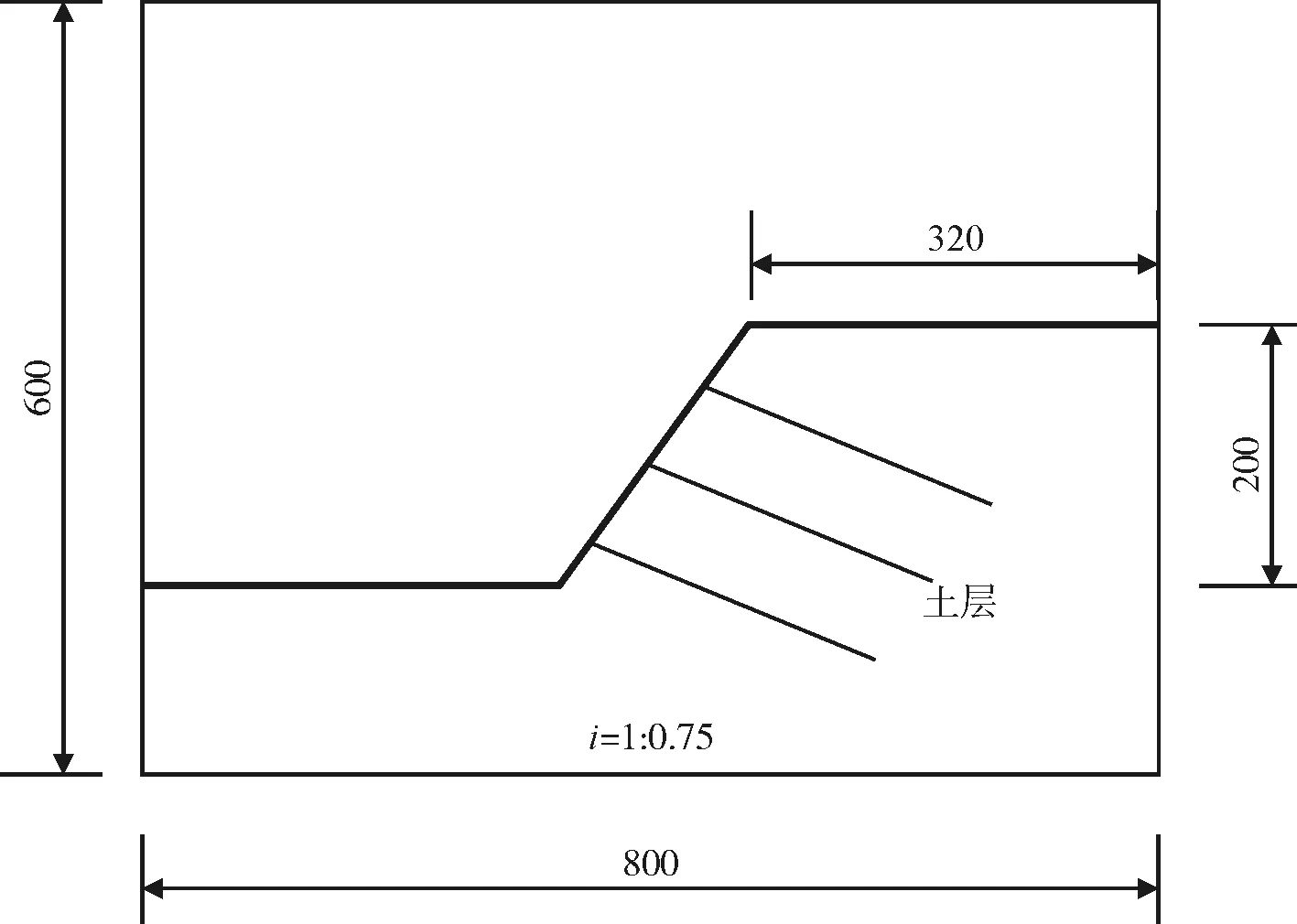
(a)边坡平面尺寸(单位:mm)

(b)制作完成的边坡模型

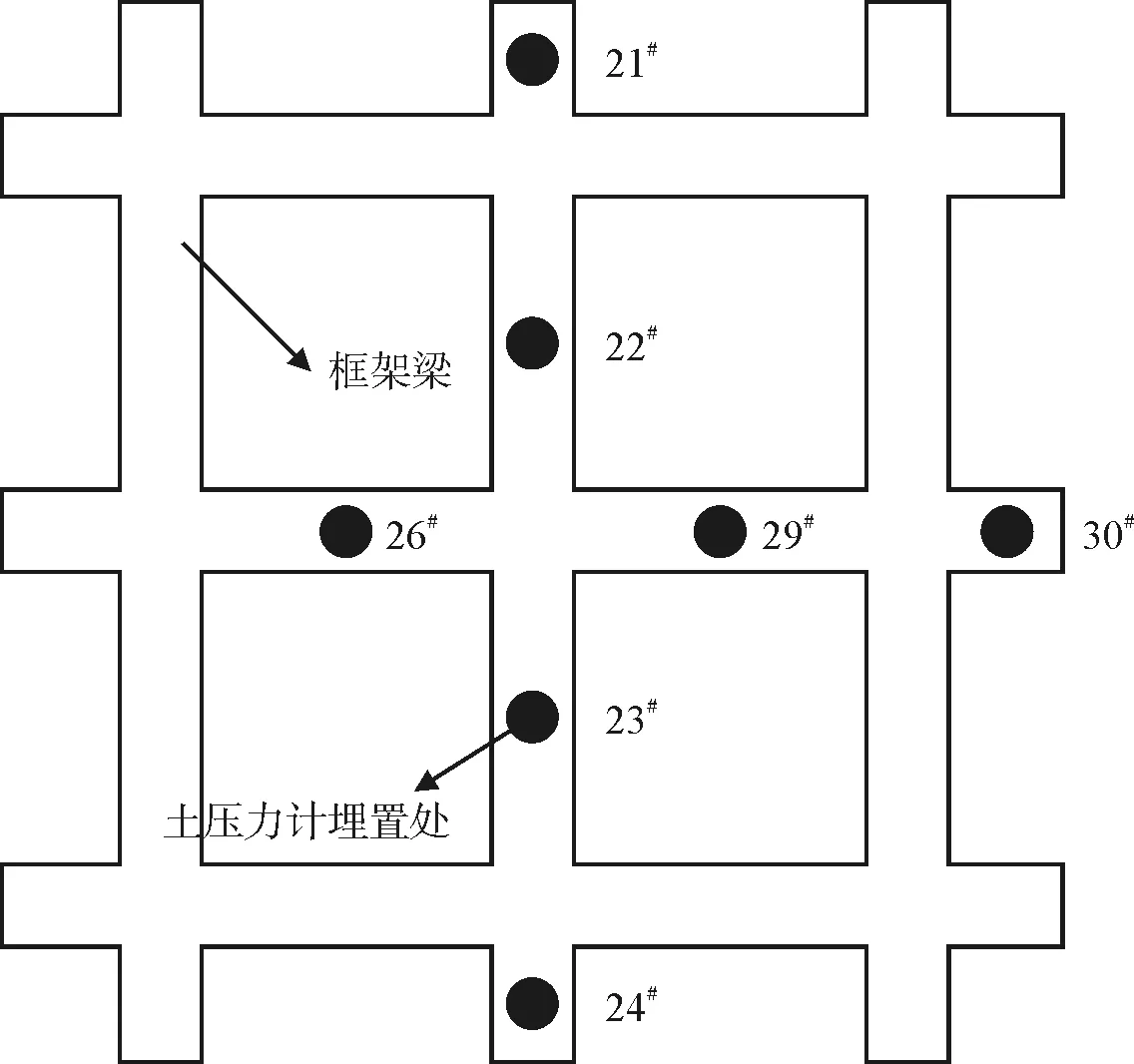
(c)土压力计方式图6 框架锚索加固均质土坡

图7 离心机加载过程曲线

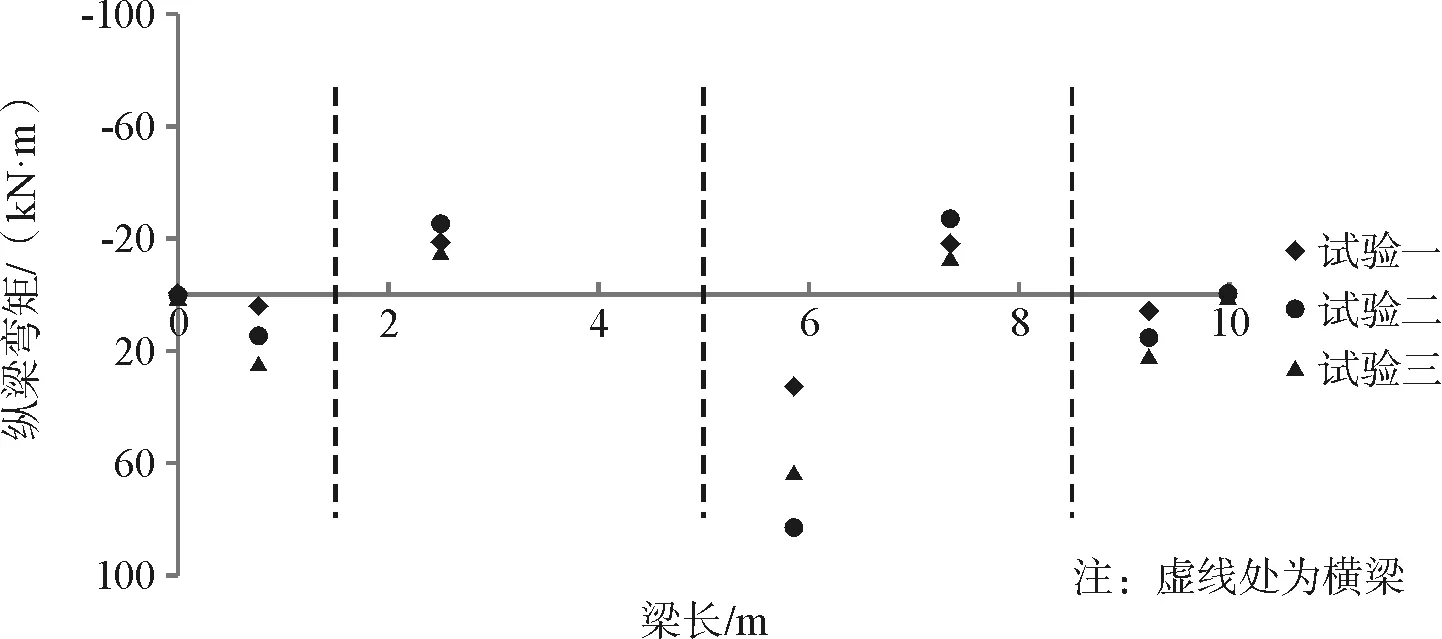
图8 框架梁纵梁弯矩变化

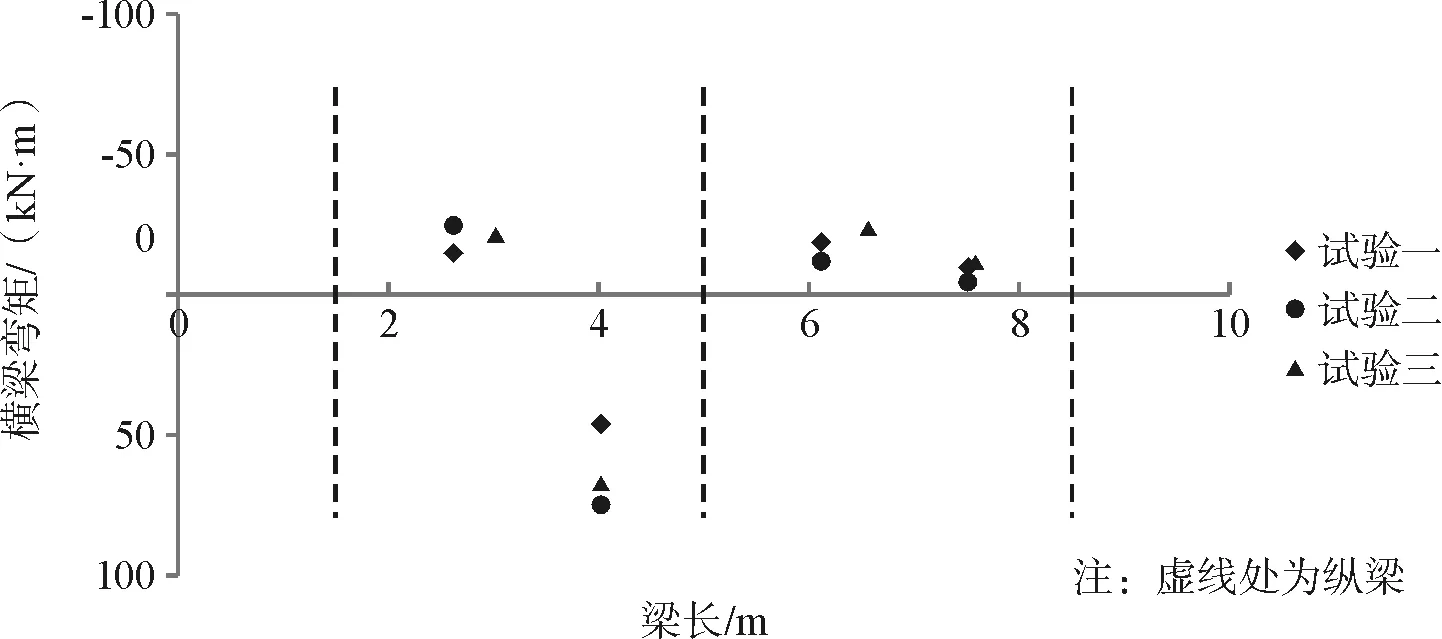
图9 框架梁横梁弯矩变化

(a)纵梁弯矩值

(b)横梁弯矩值图10 框架梁纵、横梁随锚索预应力的变化曲线

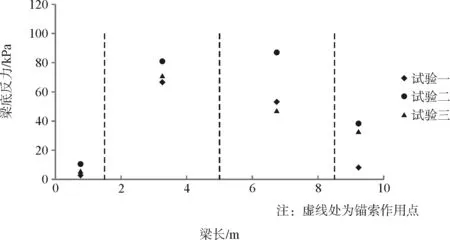
图11 框架梁下坡体压力分布

3 结论

本文详细地介绍了框架锚索加固边坡的模型制作过程和离心机试验方案，通过框架锚索加固平面滑动型边坡、基覆边坡和均质土坡的多组离心机模型试验，研究了不同边坡岩性组合及不同锚索预应力下框架锚索支护体系的受力特征和框架梁下的坡体压力分布规律。研究发现框架梁的纵、横梁均沿长度方向呈现出受拉和受压交替变换的特征，在预应力作用位置表现为较大的正弯矩，框架梁相邻预应力作用点之间受负弯矩作用，弯矩的大小与梁底边坡材料的岩土体(地基)反力系数及锚索预应力大小有关。梁底坡体压力在梁中部较大，两端较小，呈现出“两头小，中间大”变化规律，坡体材料的软硬程度、坡面平整度、施工质量均对坡体压力存在较大的影响，岩土体(地基)反力系数越大，坡体压力越小。