联合GPS与二元水声定位系统的目标定位方法

崔剑锋，刘 洋，祝令国，徐 翔，张惠文

(1.山西汾西重工，山西 太原 030000；2.大连测控技术研究所，大连 116013)

0 引 言

声波是水下信息传播的有效载体，也是目前实现水下目标定位最有效的手段.GPS利用电磁波进行定位，精度高，但对于水下目标无能为力.将GPS和水声定位系统结合起来，即可以确定水下目标的绝对位置.

1 二元式水声定位系统

二元式水声定位系统模型简单有效，是科研活动及工程实际中较为常用的一种定位合作式定位方法.

设两阵元的阵元位置为(L/2,0)与(-L/2,0),L为基阵长度，坐标系正向指向船艏方向，则可以推知合作式目标的平面坐标为

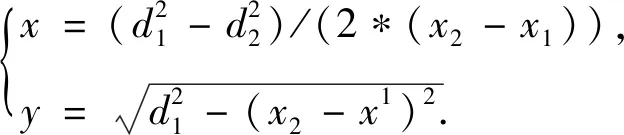
(1)

进而可以求得目标距离阵中心的距离和目标相对于船艏方向的方位角(即目标方向向量与船艏方向向量的夹角)

(2)

式中：d1,d2为目标到阵元的距离，由发射时间及检波时延可以求出.平面波情况下的算式可以得到进一步简化[1].

二元式水声定位系统应特别注意两点：① 方位模糊.直观的以式(1)为例，方位模糊指二元式定位系统解出的y实际是绝对值，真实的y坐标可以为负，因此此处的方位模糊也称为左右舷模糊.工程实际中，目标位于船的左舷或右舷通常是先验信息，由此唯一地确定y坐标.② 求解方位角.求解方位角可以利用反三角函数进行求解，因此可以有多种选择，但应注意这类函数具有不同的值域，如函数选择不当会造成求解结果错误，上述二元式水声定位系统的输出方位角范围为[0,π],据此选用反余弦函数进行计算.

2 水下目标的联合定位

要确定水下目标的绝对位置，需要以下输入参数：船的绝对位置(即水声定位系统的绝对位置)，船艏向(设定水声定位系统坐标系x正向与船艏向一致)，水声定位系统给出的目标相对方位、目标相对距离；另外需要已知试验海区位置的地球半径.

船的绝对位置可由船载GPS给出，船艏向可由罗经给出，目标相对方位、相对距离由水声定位系统给出，地球半径可代入平均值计算.

计算目标的绝对位置首先应理顺坐标方向与方位.船艏向是以正北为零度，顺时针旋转增加到360°.同样定义船坐标系下，艏向为相对零度，顺时针(即右舷)为正增加到180°，逆时针为负(即左舷)减小到-180°；据此，当目标位于右舷时，相对方位角为正值，位于左舷时，相对方位角为负值.

由图1 所示，α为目标与船艏夹角(右舷为正，左舷为负)；β为船艏向；d为目标与船的相对距离.此试验海区位于北半球、东半球，虚线为纬度线与经度线，则定义：θ=α+β，则将船坐标系旋转为平行于经纬度线的坐标系，计算得到新坐标系下的目标相对位置

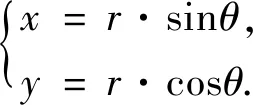
(3)

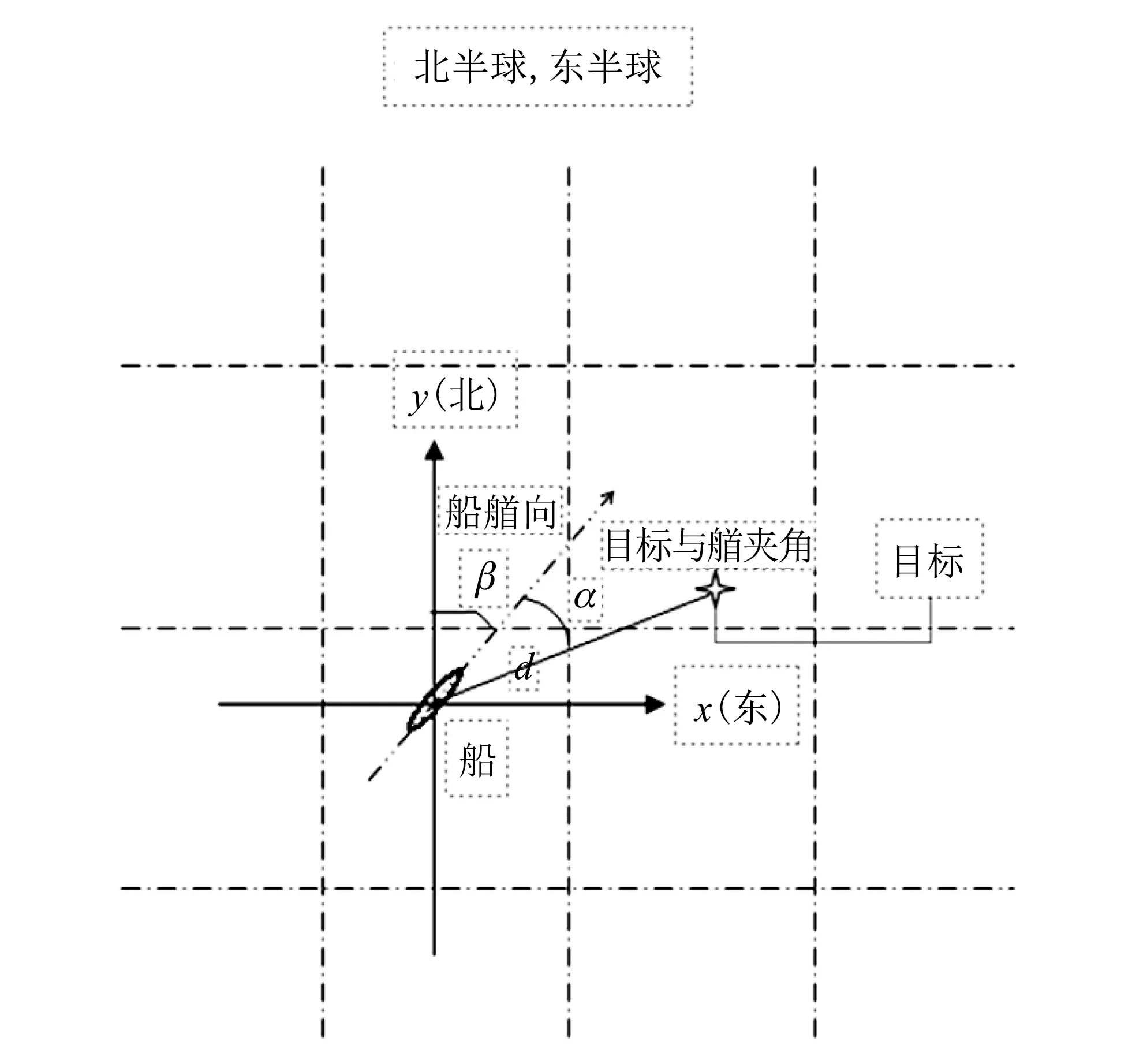
图1 目标与船艏夹角Fig.1 The angle of target and bow

当θ顺时针为正(即顺时阵旋转增加)时，对4个象限(顺时针依次定义4个象限，不同于通常的逆时针依次定义4个象限)验证，图2 中为θ以y轴为轴顺时针旋转所得角度，θ′是相应的θ所在方向与y轴所夹的锐角：

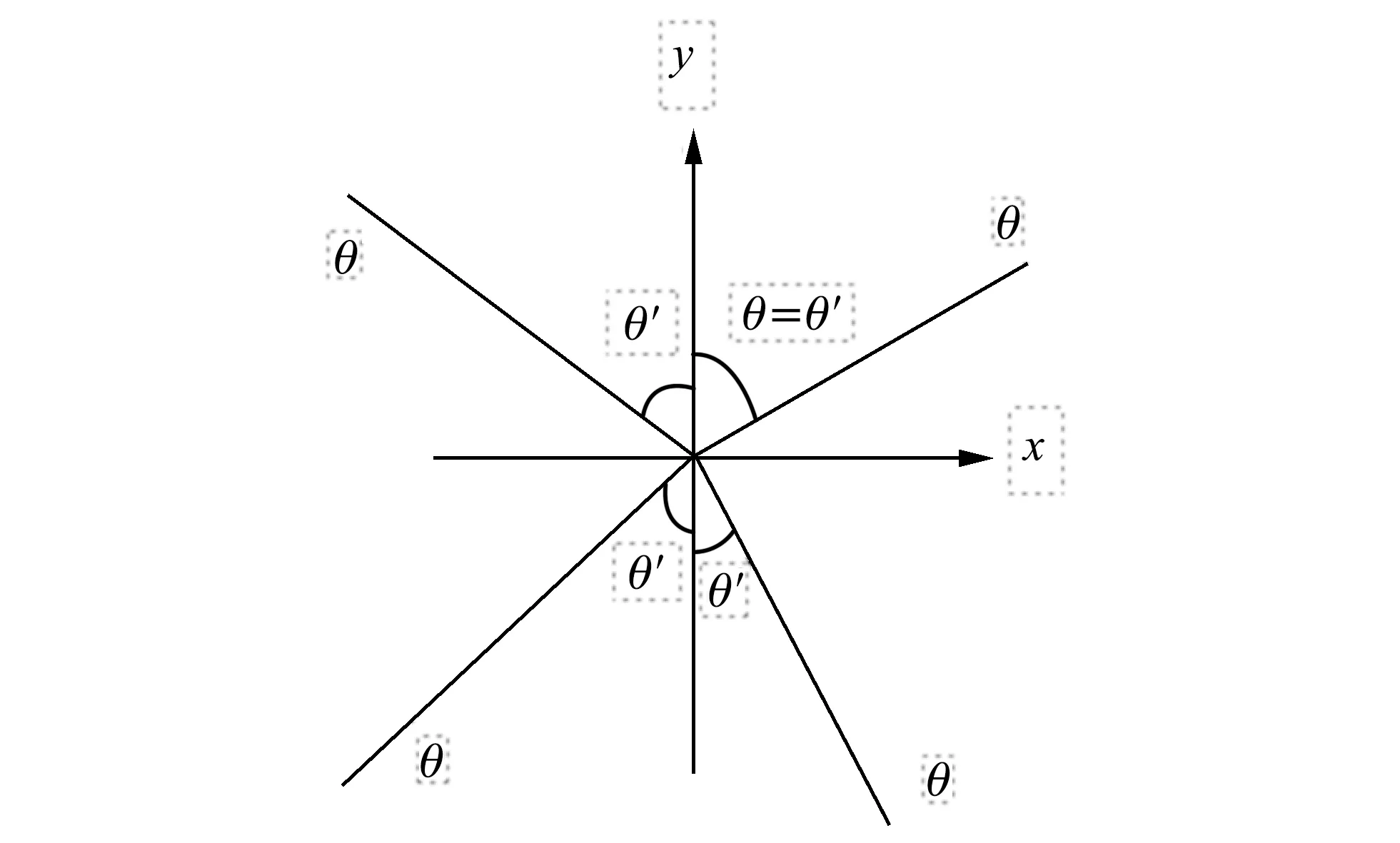
图2 角度示意图Fig.2 Sketch map of angle

一象限

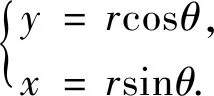
(4)

二象限

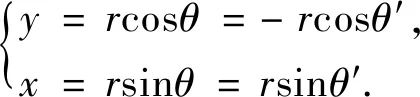
(5)

三象限

(6)

四象限

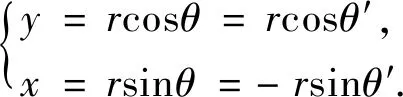
(7)

由上可知相对坐标系与东、北半球经纬度正方向一致，因此得到目标的绝对位置为

(8)

(9)

式中：N1与E1为船的经纬度；N2与E2为目标经纬度.

对定位系统基线与船艏向存在夹角的情况进行补充说明：一般而言，二元式水声定位系统的基线正向与船艏向平行，但也可能存在特殊安装或安装误差导致基线正向与船艏向也存在一个夹角，此时图2 中标记“目标与艏向夹角”即分解成两个部分：基线与船艏向的夹角加上目标与基线的夹角.需要说明的是：此时，基线与船艏向的夹角需人为判定，基线位于船的右舷为正、左舷为负；目标方向与基线的夹角也需要人为判定，目标方向位于基线右侧为正、左侧为负.依此规律将目标与艏向的夹角分解加和即可.

3 误差分析

在上述联合定位方法中，影响目标绝对位置定位精度的因素包括GPS定位误差和水声定位系统误差两个基本误差输入源[2-3].

3.1 二元水声定位系统的误差空间分布特性

对于二元水声定位系统，存在一种观点，即在基阵的小角度方位角上，由于基阵投影孔径变小，目标的定位精度可能会比较低.可以基于数值统计的方法求出定位系统的误差空间分布特性，从而对这一问题进行说明.

输入误差项包括两项：一是基阵位置标定误差，一是时延测量误差.基阵位置误差又包括阵元间距误差和阵轴、船轴夹角误差.时延测量误差又包括同步时钟误差和检波误差.

阵元间距误差、时延测量误差通过解算方程间接影响目标的距离、方位角，阵轴、船轴夹角误差则直接影响目标方位角.

设定时延测量误差和基阵测量误差，误差空间分布特性如图3～图6 所示.时延测量误差为(-1,1)m，基阵长测量误差为(-0.05,0.05)m.x轴方向为基阵轴所在方向，二元阵解算结果包括目标的直角坐标值、目标方位角、目标绝对距离4个值，各自的误差空间分布特性都不相同.在综合测量误差的影响下，x坐标的误差值呈同心圆扩大；y坐标值具有明显的指向性，在方位角小角度方向上测量误差较大；方位角测量值与y坐标有相同的趋势，在小角度方位角上测量误差大，不同于y坐标误差的是在同一个方位角上测量误差是一致的，空间分布特性呈现放射状；距离误差是几项计算值中最稳定、最小的，在相同的综合误差下，距离误差在全空间具有误差一致性.

图3 x坐标误差Fig.3 Error of x

图4 y坐标误差Fig.4 Error of y

图5 角度测量误差Fig.5 Error of angle

图6 距离测量误差Fig.6 Error of distance

因此，对方位角的测量值，前述观点是正确的，在小角度方位角上，方位角测量精度低于正横方向.其他的测量值则各有规律，不能一概而论.

3.2 联合定位解算的误差影响因素

联合定位解算程序中将地球简化为正球体，需要分析由此造成的误差影响有多大.以北纬30°附近为例进行分析.地球半径分别取6 400 km与6 371.393 km，计算两点的距离误差.

表1 地球半径造成的两点间距离解算误差Tab.1 Distance error influenced by earth radius

分析表1 即可确定，在公里级以内的联合定位中，相较于一般的待测目标，地球半径造成的解算误差是比较微小、可以忽略的.

联合解算程序中根据原点经纬度、相对偏角、相对距离3类参量解算目标经纬度.由以上分析知道相对距离的误差较小，而原点经纬度由高精度差分GPS直接测得，因此主要误差集中在相对偏角产生的误差中.

相对偏角由测量船航向角和水声测量系统测得的目标方位角相加得到，根据弧长公式d=r·θ·π/180，以距离200 m的目标为例分析误差，如图7所示.

图7 距离误差与偏角的关系Fig.7 Distance error changes with angle departure

4 结 论

对于水下定位系统：① 船载二元式水声定位系统存在左右舷模糊的问题；② 解算适宜采用反余弦函数.

在水下目标的联合定位解算中，须知：① 测量船的绝对位置(由GPS直接测量得知)；测量船的船艏向(由船载罗盘等仪器测量得知)；② 水下目标相对于测量船的方位、距离(由二元式水下定位系统得知).在解算中需要理清船左右舷、声学基阵左右侧与解算程序输入角度参数的关系.

二元式水下定位系统的误差空间分布特性分析表明：基阵轴向坐标测量误差成同心圆规律；基阵法向坐标测量误差在小角度下测量比较大；目标距离测量误差在全空间呈现一致性；目标方位角测量误差在基线小角度下的误差值较大、在空间上呈放射状.

在联合定位解算过程中，地球半径的代入误差对结果的影响较小，短距离内可以忽略，偏角误差对定位结果的影响呈线性，可认为是主要的输入误差项.