寻常一样窗前月 才有梅花便不同—赏析2016年高考数学新课标全国I 卷文科第14 题

广东省佛山市南海区西樵高级中学(528211)陈国毫

三角函数作为高中数学的主体内容之一,呈现出与其他基本初等函数不一样的特征,其中最能体现三角函数的显著特性——周期性.在高中数学课程中,三角函数、三角恒等变形与解三角形是相对独立的三个部分:三角函数首先是几何的,其次是函数的,还是运算的(三角恒等变换)[1].原因是锐角三角函数是为研究各种几何量之间关系而发展起来的,是解决三角形问题的工具;而任意角三角函数不仅仅局限于此,它是最本质、最给力的周期函数,是为了研究周期现象而发展起来的,是研究现实世界中周期变化现象最典型的函数模型;而三角恒等变换是三角函数的延伸,更准确地说是同角三角函数关系式深化而来,事实上,三角问题中遇到的更多是不同角、不同名之间的关系,如何将不同角、不同名变换为同角、同名是三角函数需要继续研究的课题,因此三角恒等变换顺势而生,其既是实际情况所需,也是完善知识系统的必然[2].课标全国卷也非常注重对三角函数内容(三角函数概念的三种表征、图象与性质、三角恒等变换、解三角形)的研究,并且在研究的过程中体现对数学抽象、数学运算、逻辑推理等核心素养的考查.限于篇幅,本文只研究三角恒等变换.以下结合一道高考题,谈谈个人的思考.

1 原题展示

例1(2016年高考数学新课标全国I 卷文科第14 题)已知θ是第四象限角,且则

2 题目分析

本题以三角函数为载体,考查学生对三角函数的基本关系、诱导公式、恒等变形及一般角的概念的掌握情况和运用的熟练程度.以下从5 个小方面加强对问题的进一步认识:

(1)试卷位置:该题处于填空题第二题的位置,难度不大;

(2)问题形式:题干给出一个角与定角的和的正弦值,并结合该角是第四象限,理论上这个角就确定,即为已知角,根据三角函数与恒等变换的基本公式,理论上可以求出这个角与任意给定角的三角函数值;

(3)核心思想:注重了对三角函数背景下转化与化归思想的考查;

(4)思路呈现:从已知角的函数值出发,求出未知角的函数值,或者建立已知角与未知角之间的关系,也可以建立目标函数值与已知函数值的关系,实现“弦化切”或者“切化弦”;

(5)解题方法:基于对三角函数首先是几何的,其次是函数的,还是运算的(三角恒等变换)这种认识,立足上述解题思路的呈现,将选择从不同的角度切入,运用不同的方法进行求解.

3 解法剖析

(1)方程的思想

从已知角的函数值出发,求出未知角的函数值,通过解方程,实现“弦化切”.

(2)齐次式构造tanθ

通过对三角函数式结构特征进行分析,构造tanθ,实现“弦化切”.

由(sinθ+cosθ)2=得则即上下同时除以cos2θ,可得解得或tanθ=-7,因为θ是第四象限角,则sinθ ＜0,cosθ ＞0,又sinθ+cosθ ＞0,故cosθ ＞|sinθ|,故0,故则

(3)辅助角公式

关注目标函数值与已知函数值之间的关系,建立未知与已知的关系,实现“切化弦”.

(4)构造对偶式[3]

通过构造三角函数式的对偶式,运用方程的思想进行求解,达到简化运算的目的,实现“弦化切”.

设sinθ -cosθ=m,由θ是第四象限角,则m ＜0,联立两式平方并相加可得则故解得故则

(5)三角函数的定义

设θ角终边上任意一点P(x,y),|OP|=r(r ＞0),则由可得得即7x2+ 50xy+ 7y2= 0,得x=-7y,或x=即或tanθ==-7.因为θ是第四象限角,则sinθ ＜0,cosθ ＞0,又sinθ+cosθ ＞0,故cosθ ＞|sinθ|,故-1=tanθ ＜0,故tanθ=则

(6)等差中项的性质

因为cosθ ＞0,可设公差d ＞0,则sinθ=由sin2θ+cos2θ= 1,得= 1,解得d=由d ＞0,可得则sinθ=-cosθ=,故tanθ=则

(7)数形结合

从解析几何的观点看题目的已知与未知条件,通过转化代数式,使其赋予几何意义,利用解析几何的知识工具进行求解.

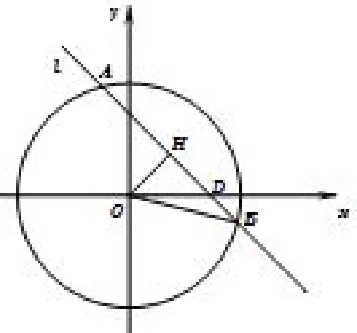
图1

由sinθ+ cosθ=设sinθ=y,cosθ=x,则x+y=则问直线l:与圆O:x2+y2=1的交于A,B两点.由于θ在第四象限,故θ= ∠DOB.点O到直线l的距离为:而OB= 1,则在R t△OHE中,HE=故tan ∠HOB=又因为kl=-1,则∠HOD= 45°,则tanθ= tan(∠HOB -∠HOD)=tan因为θ在第四象限,故则tan

(8)配凑角

法一由sinθ在第四象限,则在第一象限,则则,故则

法 二由θ在第四象限,则在第一象限,则由则故

这里,我们对配凑角的方法作如下思考:

①如何想到用配凑角的方法

题干给出一个角θ与定角的和的正弦值,并结合θ是第四象限,理论上θ这个角就确定,即为已知角,当然也确定.这时就可以建立这四个角的关系.

②如何进行配凑角

(i)局部配凑角

局部配凑角,是针对已知角与未知角进行的一种配凑,不将目标函数的角进行整体处理,而是局部运算.方法一是基于已知角的函数值,求出未知角θ的函数值,采用局部配凑,建立这三个角的关系,即通过得出θ=进而得到

(ii)整体配凑角

整体配凑角,是针对已知角与目标函数的整体未知角进行的一种配凑,直接建立两者的关系,一步到位.方法二的出发点是直接沟通采用整体配凑,建立已知角与未知角之间的关系,.两角尽管没有体现互余或者互补的关系,但两者相差也非常有利于借助诱导公式进行运算,即进而得到

③配凑角后想达到什么效果

事实上,通过局部的配凑角,或者通过整体的配凑角,都是为了进一步显化未知与已知的关系,当未知与已知的关系式变得更加清晰,那么对整个问题的处理将更加明朗,都有利于降低整体的运算量,使得运算的过程更加简单简洁.

④配凑角的实际操作

从上述的解法与分析,配凑角的方法带来了以“整体→局部→整体”或者“整体→整体”的眼光看待未知与已知的关系,对学生分析问题的能力以及如何处理好整体与局部、整体与整体的关系的能力有了进一步的提升,对学生的思维水平有一定的提高.另一方面,尽管未知与已知的关系显化,但是在实际教学中,学生对该配凑角的方法掌握得不扎实,一是缺乏对已知角与未知角的关系的敏锐判断,二是尽管运算的过程相对简洁,但是两个整体角的关系表现形式的相对复杂性使得学生在心理上产生了一定的畏惧,运算过程不尽人意.笔者也反复思考,在立足配凑角的方法的基础上,如何更好地对配凑角有更好的认识?

⑤配凑角的本质

经验表明,通过配凑角整体处理角,涉及的两角往往互余、互补,或者相差某个特殊角或者是一个倍数关系;从函数的角度,研究的两个角实际上具有简单的线性关系,也就是说即使两个角的表现形式可能稍微有些复杂(可能带有倍数或者辅助角),但都可以通过线性关系表示两者,即为一次函数的关系式.因此,笔者认为,配凑角的本质,实际上就是换元法,通过换元,不仅依旧可以保持两个角的内在联系,而且在形式的呈现上显得更加简洁明了.

以下采用换元法处理该问题:

(9)换元法

4 背景探源

在对上述问题的解决的过程中,我们经历了从方程、函数、数列、几何等多个方面对问题进行了思考,并强调、重视了通性通法,回应了三角函数既是几何的,也是函数的,还是运算的观点,充分体现了化归与转化的思想.对于该题,尽管解法丰富多彩,通俗易懂,但笔者意犹未尽,下面继续探寻其三角函数式结构,挖掘问题的本质.

(1)两角和差三角函数的结构对比与分析

为了描述方便,采用其中一种结构:两角和的三角函数结构,即sin(α+β),cos(α+β),tan(α+β),并定义α为主元,β为辅助角.在教学中,在众多的高考题或者地方模拟题中,辅助角β常常以的形式出现,比较少采用其他特殊角,如或者等等.即三角函数式为这三种函数模型居多,其用意为何? 笔者认为有以下2 点原因:

①数学的美

由sin可得从三角函数式的表现形式上看,式子结构显得更加和谐、简洁、体现出数学的美;

②方程的美

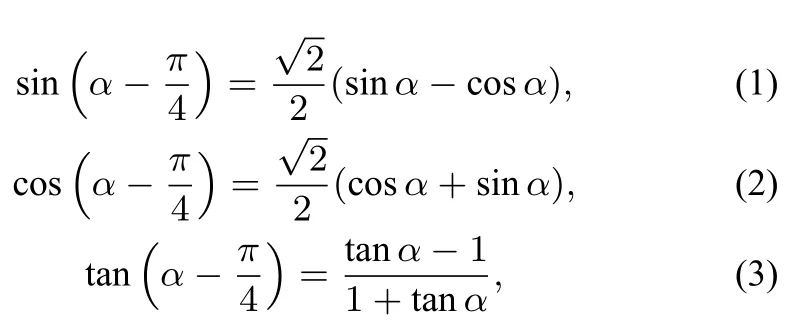
从方程的角度,(i)与(ii)的未知数有2 个,而(iii)式的未知数只有1 个.

若实现由单角到单角的方程运算,显然(iii)式在运算的操作性上更有优势,即通过(iii)式可得tanα →sinα=k·cosα,结合sin2α+cos2α=1,联立方程组即可求解其他单角三角函数值;而(i)与(ii)的未知数有2 个,所以更多情况下得到tanα →sinα=k·cosα+m(k=±1,m ∈R),其与sin2α+cos2α=1 构成的方程组在运算求解上会稍微有点困难;因此(iii)式在进行单角到单角的方程运算中有较大的优势,具有较好的操作性和可行性;

若实现由单角到倍角的方程运算,则(i)与(ii)式更显优势,由(sinα±cosα)2= 1±sin 2α,即通过两边平方实现单角转化为倍角,而且可喜的是转化后的方程就只有一个未知数sin 2α,这对解方程无疑是最好的表达方式,从而可求解其他倍角三角函数值,即经历(sinα±cosα)2→sin 2α/cos 2α/tan 2α;若是通过(iii)式进行单角到倍角运算,则需要经历tanα →sinα →cosα →sin 2α/cos 2α/tan 2α的思维过程与运算过程.

限于篇幅,以下各出几个题目供大家思考:

2、(2013 全国理2卷15题)设θ为第二象限角,若则sinθ+cosθ=____.

3、(2013全国文2卷6题)已 知sin 2α=则

4、(2012全国理2卷7题)已 知α为第二象限角,sinα+cosα=则cos 2α=( )

A.B.C.D.

5、(2017全国文3卷4题)已知sinα-cosα=则sin 2α=( )

A.B.C.D.

(2)运用上述“方程的美”重新审视例1

(3)揭示本质

三角函数首先是几何的,其次是函数的,还是运算的(三角恒等变换).依旧立足于对三角函数多层次观点,回归到最原始的位置,从几何的角度欣赏该题,如图所示,可以发现表示直线OA的斜率,即表示直线OB的斜率,即由于OA⊥OB,根据解析几何的知识,有kOA·kOB=-1,即故

图2

(4)命题思路

通过对结构的分析以及本质的认识,对于例1,即2016年高考数学全国I 卷文科第14 题,该题的命制背景是解析几何的直线位置关系的问题,本质上是斜率存在两条直线互相垂直,斜率之积为-1,通过三角函数的解析表征作为载体,命制了该问题,具体的思路应是要求只需给出的值即可,而为了进一步考查考生的数学运算、逻辑推理等核心素养以及突出函数与方程的思想、化归与转化的思想,命题者给出的是时,能够有不同的切入口,不同的方法来解决该问题.

(5)几何式子三角函数化

斜率存在的两条直线互相垂直,斜率之积为-1,其三角函数的展现形式为的值,这样便让考生面对或者如在正切值存在的情况下,有:基于此结论可以构造、命制很多三角恒等变换问题.

5 横向联系

以下给出类似的三角恒等变换问题,进一步探索挖掘其中的关系.

例2(2013年高考数学浙江卷理科第6 题)已知α ∈R,sinα+2 cosα=则tan 2α=( )

对于该题目的解法,可用上述介绍的方法进行求解,这里不一一展开.为了研究接下来的问题,这里直接简单地给出的求解过程:由sinα+ 2 cosα=结合sin2α+ cos2α= 1,可 解 得tanα=或tanα= 3,则当时,代入运算可得当tanα= 3 时,代入运算可得于是

(1)疑惑产生

在求解本题目时,当得出tanα的取值有两个的时候,结合选项的答案唯一,不自觉产生一个想法:两个tanα的值应该要舍去一个,检验了题目的条件,才发现α ∈R,不能对tanα进行舍弃,即两个都符合题意,而通过代入求解运算tan 2α,最终的答案居然一致.笔者对此很好奇,为什么不一样的答案代入后,会有相同的结果? 根据经验,很多时候不同的答案代入,最终的结果是不同的.于是产生这样的问题,当tanα的两个值满足什么的条件,tan 2α的值唯一?

(2)回归教材

本着高考立足教材的理念,笔者回归教材,试图在教材寻找关于tanα与tan 2α的单独的求值运算.翻阅必修四第三章《三角恒等变换》的全部内容,没有找到直接以“已知tanα,求解tan 2α”的形式呈现的例题或者课后练习题.倒是在教材第3.1.3 节《二倍角的正弦、余弦、正切》的课后练习第135页发现了第4 题:

例3(教材必修4 第135页练习第4 题)已知求tanα的值[4].

尽管不是要寻找的“已知tanα,求解tan 2α”的形式,但是跟问题很接近了.再细想,这就是笔者要寻找的答案“tan 2α的值唯一,tanα满足什么条件”.由二倍角公式得解 得或tanα=-3-也就是说,tanα=-3 +或tanα=-3-也能使得tan 2α的值唯一.

(3)问题与猜想

为了研究方便,将上述两个问题提取,归纳出问题:

①若tanα=或tanα= 3,则tan 2α=是唯一值;

② 若tanα=-3 +或tanα=-3-则也是唯一值.

问题:若tanα1与tanα2满足什么条件,则tan 2α唯一? 通过对两个tanα重新进行四则运算的尝试,有以下规律:两个tanα值相乘都满足:于是猜测:若tanα1·tanα2=-1,则tan 2α的值唯一.

(4)挖掘本质

图3

在经历了例1 的背景与本质:斜率存在的两条直线互相垂直,斜率之积为-1.笔者决定从解析几何的角度,对问题进行探究.设直线OA的斜率为klOA= tanα1,直线OB的斜率为klOB=tanα2,由于tanα1·tanα2=-1,故直线OA⊥OB,即对于tan 2α,如图,2α= 2α1= ∠A′Ox,或者2α=2α2=∠B′Ox,则tan 2α=kOA′或tan 2α=kOB′,由于故2α1+2α2= 2(α1+α2)=π,说明∠A′OB′=π,即A′,O,B′三点共线.故2α的终边OA′、OB′落在同一直线A′B′上,由于直线A′B′的斜率唯一,故tan 2α的唯一.由此可见,例2,例3 的本质也是斜率存在的两条直线互相垂直,斜率之积为-1.

以上便是笔者关于三角恒等变换的一些思考,题目立足教材、来源高考,从考查的要求,命题者希望强调通性通法,突出转化与化归的思想;从教育工作者的角度,应该站在不一样的观点来重新认识、审视这些司空见惯的问题.“寻常一样窗前月,才有梅花便不同”,三角函数是几何的,其次是函数的,还是运算的(三角恒等变换),有了这样的观点指导,平平常常的东西也能品出不一样的芬芳;有了新的角度,问题的联系,知识系统的形成才会更加完善.