Budyko-Fu模型下气候季节性指标中水热变化时相差的选取研究

常斐杨，刘文兆,，周海香，宁婷婷

(1.西北农林科技大学水土保持研究所，陕西 杨凌 712100； 2.中国科学院水利部水土保持研究所，黄土高原土壤侵蚀与旱地农业国家重点实验室，陕西 杨凌 712100；3.中国科学院西北生态环境资源研究院，内陆河流域生态水文重点实验室，甘肃 兰州 730000)

流域水量平衡、气候波动和植被变化是相互作用的，深入了解这种相互作用对于流域水量平衡过程分析非常重要[1-2]。在这方面研究中，Budyko理论[3]得到了广泛应用，特别是其量化降水分配为蒸散和径流的比例关系的做法[2,4]。Budyko理论在发展过程中出现了不同形式的参变量，譬如Budyko-Fu公式[5-6]中的参数ω和Budyko-MCY公式[7-8]中的控制参数n，已发现这两个参数具有线性相关性[8]。Yang等[9]选取了中国108个流域的多年平均实际蒸散发量、降水量及潜在蒸散发量数据，求出Budyko框架下各公式中的参数值，比较认为Budyko-Fu公式能较好地表达各流域水热耦合平衡关系特征。

Budyko-Fu公式中影响参数ω的因素有地形[10-12]、土壤特性[1，13-14]、植被[2，15-17]、土壤-植被平均蓄水能力[1，17-18]、降水强度[1]和气候的季节性[1，4，13，19]等。对同一流域而言，在年际过程中，土壤特性和地形的变化很小，可以忽略，而植被的变化比较显见，其对控制参数的影响较为显著[20]。杨汉波等[19]在Budyko框架下，结合气候季节性指标与相对土壤入渗能力指标，提出了一个参数ω的表达式。Ning等[4]建立了参数ω与植被盖度及气候季节性指标间的一个表达式。Liu等[21]基于Berghuijs和Woods[22]的工作，在气候季节性指标中考虑水热变化的相位差的影响，取得了较好的结果。

本研究在Budyko-Fu框架下，对3种气候季节性指标进行对比，探讨气候季节性指标中水热变化时相差的选取方法，进而改进参数ω的半经验公式，说明在流域径流模拟计算中不同气候季节性指标的应用效果。

1 研究区域与方法

1.1 区域概况

泾河为渭河的第一大支流，居黄河中、上游地区，全长455.1 km，流域面积45 421 km2(106°14′～108°42′E，34°46′～37°19′N)(图1)，横跨宁夏、甘肃、陕西三省的部分地区。流域内地势东南低、西北高，可分为西南部山地林区、东南部山地河川区、中部黄土塬区和残塬区以及北部黄土丘陵区。泾河流域为典型的温带大陆性气候，地处半湿润气候向半干旱气候的过渡区，多年平均气温为8℃，多年平均降水量为508 mm，干燥指数为2.09。流域内地表植被稀疏，长期以来水土流失严重，生态环境脆弱。

1.2 数据来源

本研究选择泾河流域及其周边18个气象站点1981-2011年的气象资料来进行计算分析，主要包含：降水及计算潜在蒸散的空气温度、风速、相对湿度等。气象数据来源于中国气象数据网(http://data.cma.cn/)。采用泰森多边形法来计算流域平均降水和潜在蒸散。1981-2011年月径流量数据来源于张家山水文站(泾河流域出口控制站)，其控制面积43 216 km2。泾河流域径流年际变化过程如图2示。用1981-2011年GIMMSNDVI3g数据集(https://ecocast.arc.nasa.gov/data/pub/gimms)中的NDVI来反映植被覆盖状况，空间分辨率为8 km，时间分辨率为15 d。

图1 泾河流域水系及气象、水文站分布图Fig.1 Water system， meteorological and hydrological stationsin Jinghe River catchment

图2 1981-2011泾河流域径流年际变化过程Fig.2 Inter-annual variation of stream flow in Jinghe Rivercatchment during 1981-2011

1.3 Budyko-Fu公式中的控制参数

傅抱璞[5]在Budyko假设的基础上，通过一系列的数学推导，给出了流域实际蒸散量的解析表达式：

(1)

式中，ET、ET0和P分别为流域年实际蒸散量、年潜在蒸散量和年降水量。ω为体现除P、ET0之外的其他因素影响的参变量。式中的变量均采用自然年计算。

式(1)中年实际蒸散量(ET)采用流域水量平衡公式计算：

ET=P-R-ΔW

(2)

式中，R和ΔW分别为流域年径流量和流域蓄水变化量(计算时段末与时段初之差)。长时间尺度上ΔW可以忽略，本文在年际尺度上近似取ΔW=0。

式(1)中年潜在蒸散量(ET0)采用Penman式计算[23-24]：

(3)

(4)

f(U2)=0.26(1+0.54U2)

(5)

式中，ET0为流域潜在蒸散量(mm·d-1)；Δ为饱和水汽压和气温曲线的斜率(kPa·℃-1)；γ为干湿表常数(kPa·℃-1)；Rn为净辐射(MJ·m-2·d-1)；G为土壤热通量，在日尺度上假设为0(MJ·m-2·d-1)；U2和Uz分别为高度2 m和高度Zm处的风速(m·s-1)；Z为实测风速高度(m)，本文中为10 m,这时U2=0.795U10；es和ea分别为空气饱和水汽压与实际水汽压(kPa)。结合公式(1)、(2)、(3)反推出参数ω。

1.4 气候季节性指标

Walsh和Lawler[25]为了反映降水的季节性变化，提出了气候季节性指标SI1：

(6)

地球自转平面(赤道面)和公转平面(黄道面)夹角(黄赤交角)的存在使得太阳直射点在南北回归线间移动是气候季节性发生的根本驱动力。这种驱动力使得在赤道以外区域的多数气候因子都随太阳辐射呈现出正弦变化的规律。因此，Milly[1]假定的年内水分和能量的供应服从如下正弦分布：

(7-1)

(7-2)

式中，τ为变化周期，赤道以外取值1，赤道取值0.5；t为时间，以月为单位，取4月为初始值0,赤道以外单位月份弧度值为π/6；P和分别为月平均降水量和月平均潜在蒸散量；δP和δET0分别指相对于年内降水量和潜在蒸散量月均值的相对振幅，代表了二者在年内的变化幅度。将和分别与sin[πt/(6τ)]拟合即可得到δP和δET0。

随后，Woods[27]将P和ET0的差值进行无量纲化：

(8)

并定义了气候季节性指标SI2：

SI2=|δP-δET0φ|

(9)

Liu等[21]参考了Berghuijs和Woods[22]提出的年内降水相位(SP)和潜在蒸散量相位(SET0)变化的概念(式(10-1)，(10-2))，在Milly[1]和Woods[27]提出的气候季节性指标SI2的基础上，定义了气候季节性指标SAI：

(10-1)

(10-2)

(11)

式中，SP与SET0分别为年内月降水量与月潜在蒸散量的时相位移，与式(7)对比可知，二者分别相当于月降水量与月潜在蒸散量取月平均值时的月份时间。本文在参考Liu等[21]的方法的基础上，相位进一步计算到小数位，拟合时SP与SET0依次取1.0，1.2，1.4，…，5.6，5.8，6.0进行试算，取对应决定系数最高的SP与SET0作为时相位移值代入式(11)计算。

2 结果与讨论

2.1 现有3种气候季节性指标与参数ω的关系比较

以SAI1表示按各年的降水与ET0分别确定的相位差计算的SAI值。利用30年间泾河流域的潜在蒸散量和降水量数据计算得到气候季节性指标SI1、SI2以及SAI1，3种指标与Budyko-Fu公式参数ω的关系如图3所示。在逐年SI1计算中，式(6)中的P、Xi分别取计算年份的年降水量与月降水量。SI1、SI2与参数ω均呈极显著相关(P<0.01)。其中，指标SI1与参数ω呈极显著正相关，决定系数为0.343；指标SI2与参数ω呈极显著负相关，决定系数为0.508。指标SAI1与参数ω呈显著相关关系(P<0.05)，决定系数为0.206。

Walsh和Lawler[25]认为降水的季节性主要表现在：(1)绝对季节性(干季与湿季)；(2)相对季节性(无明显湿季)；(3)年内最大降水量和最小降水量；(4)年内最大降水量和最小降水量持续时间；(5)年内降水量分布的变异性和稳定性。他们提出气候季节性指标SI1来描述降水的季节性变化特征，但指标SI1仅考虑到了年内降水量的季节性变化，忽略了潜在蒸散量的季节性变化。而后Milly[1]和Woods[27]提出的气候季节性指标SI2同时考虑了年内降水量与潜在蒸散量的季节性变化，故指标SI2对流域年内水热变化的描述比指标SI1更准确。指标SAI1在指标SI2的基础上考虑到了年内降水量与潜在蒸散量变化的不同步性，即雨热不同期，因此理论上相较于指标SI2更准确，指标SAI1与参数ω的关系应当更好。但在本研究中，逐年计算相位差得到的指标SAI1与参数ω的相关性没有达到预期的效果。

2.2 年际变化过程中水热季节相位差的特点与正弦模拟

在年际尺度上计算指标SAI1时，每年选取的降水量与潜在蒸散量相位，即Sp和SET0都不同，但气象因子随时间是连续变化的。图4表示的是1990-01～1992-12连续36个月的月降水量变化情况。由多年平均情况确定时相进行正弦模拟时，任取连续12个月，其峰谷时相间距有正弦等距特点，相邻波峰与波谷间距均为6个月，相邻波峰与波峰间距均为12个月;但当时相不固定时，则不具有这一特点。例如从1990年波峰开始至1992年波峰，按自然年分别选取相位，相邻波峰与波谷的间距分别为4.8个月、6个月、7.2个月和6个月，相邻波峰与波峰的间距分别为10.8个月和13.2个月。确定时相位移数值过程中，如果每年的起始月份发生变化，则同样时间段会有不同的相位计算结果。例如非固定相位时，自然年下计算1990、1991和1992年月降水量的时相位移分别为4.4、3.2和4.4，而若以上一年9月至当年8月为1个年份进行计算，则1990-09～1991-08和1991-09～1992-08的时相位移分别为4和4.2(图4)。因此，本文认为在相同流域用正弦函数模拟降水量与潜在蒸散量的变化趋势时，应由二者多年平均值确定其相位，逐年计算SAI时取固定相位差时整体效果较好。如果逐年分别计算相位，虽然各年的实测值与模拟值吻合较好，但年际过程上模拟的相位与实际的波动起伏会有较大差别，整体上不如采取多年平均状况固定相位的结果。

图3 气候季节性指标与Budyko-Fu公式参数ω的关系Fig.3 Relationships between climate seasonality indexes and parameter ω in Budyko-Fu equation

2.3 固定相位差时SAI的计算及其与控制参数ω的关系

根据对同一流域年际变化过程中水热季节变化相位差特点的分析，这里用降水量与潜在蒸散量的多年值确定其二者的时相位移，即Sp和SET0值。随后以固定的Sp和SET0值计算每年的δP和δET0值，最终计算逐年的SAI值，以SAI2表示。SAI2与参数ω之间呈极显著相关，决定系数达到0.626(图5)，相较于非固定相位的SAI1的决定系数0.206及不考虑相位差别的SI2的决定系数0.508有了较大的提高。说明利用正弦函数模拟相同流域降水量与潜在蒸散量的变化趋势时，采取固定相位较好，这样保证了任意连续时段上模拟曲线的正弦相位特点。

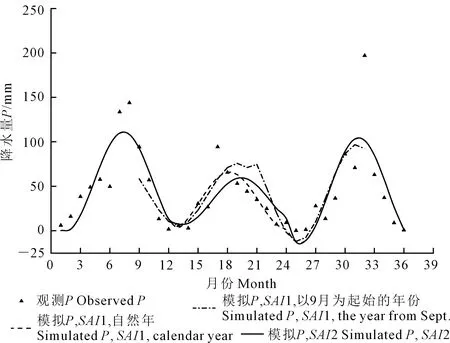
图4 1990-1992年泾河流域月降水量实测值与固定相位及非固定相位时正弦模拟值Fig.4 Observation and sinusoidal simulation with fixed andunfixed phases of monthly precipitation in Jinghe Rivercatchment during 1990-1992

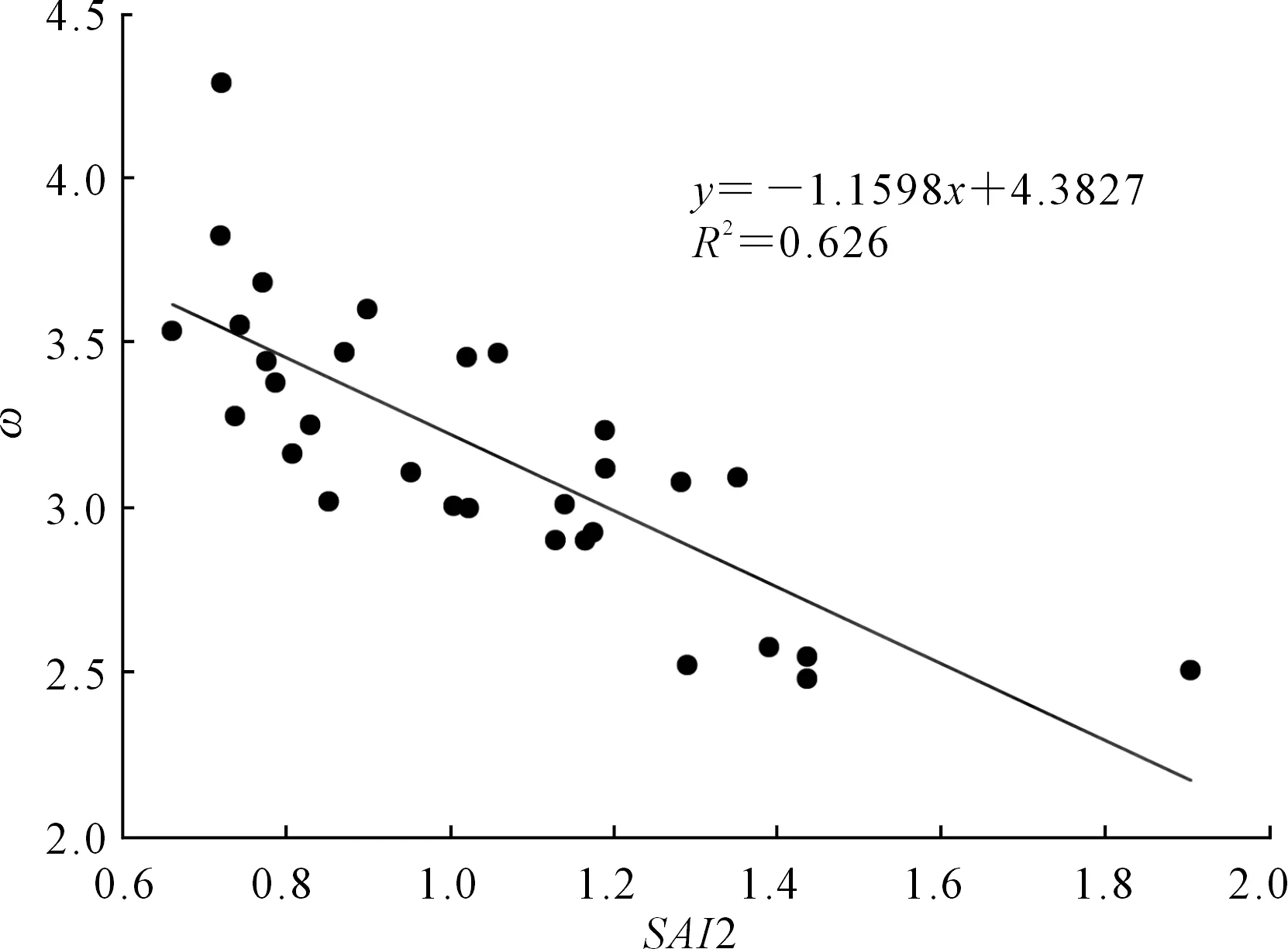
图5 固定相位下气候季节性指标(SAI2)与Budyko-Fu公式参数ω的关系Fig.5 Relationship between climate seasonality index (SAI2)with fixed phase and parameter ω in Budyko-Fu equation

2.4 Budyko-Fu公式参数的半经验公式改进及其在流域径流年际变化模拟中的应用

参考Ning等[4]给出的参数ω与植被盖度和气候季节性指标的半经验公式的一般形式，以NDVI直接表示植被覆盖度，以幂函数表示参数ω随NDVI指标的变化规律；考虑SI2取值特点，由指数函数表示参数ω随SI2指标的变化规律。通过回归分析求得NDVI及SI2与参数ω的半经验式(12)，其决定系数达0.658。

ω=1+8.559NDVI1.055×exp(-0.407SI2)

(12)

用非固定相位计算的指标SAI1代替指标SI2，则得到式(13)所示结果，其决定系数为0.322；用固定相位差计算的指标SAI2代替指标SI2，则得到式(14)，其决定系数达到0.746。式(14)相较于(12)和(13)两个式子，决定系数有了较大的提高，说明固定相位下指标SAI2比非固定相位下指标SAI1和指标SI2更能准确表达该流域气候季节性变化的影响。

ω=1+12.013NDVI1.346×exp(-0.192SAI1)

(13)

ω=1+11.681NDVI0.994×exp(-0.542SAI2)

(14)

考虑图3(a)中ω与SI1的散点图特征，以幂函数形式表达SI1对ω的影响，进而给出相应的ω的表达式如下，其决定系数为0.485。

ω=1+11.953NDVI1.382×SI10.723

(15)

通过公式(12)、(13)、(14)和(15)分别计算出参数ω，再结合P与ET0通过Budyko-Fu公式计算出4个径流的年际序列，将其分别称为RSI2、RSAI1、RSAI2和RSI1，比较其与实测径流系列(Ro)的差别，由表1给出比较结果的统计特征，包括平均值、极差、标准差和平均绝对误差，由于1981年DNVI数据缺失，表1、表2只给出了1982-2011年的相关计算结果。

表1 1982-2011年RSI2、RSAI1、RSAI2、RSI1与Ro的统计特征

表2 2000年前后RSI2、RSAI1、RSAI2、RSI1与Ro的平均绝对误差对比

整体来看，4个气候季节性指标对流域径流年际变化的模拟效果以SAI2表现较好，其径流模拟值的平均值、极差和标准差都最接近实测值，平均绝对误差最小。另外分析径流的年际变化趋势，发现2000年之前模拟径流与实测径流的吻合程度大体上都要高于2000年之后，只是在SI1的模拟结果中两个阶段的误差大体相当。

SI1只考虑降水季节变化特征，突出了降水时间变异的影响，其用于径流模拟时在2000年前后误差大体保持一致，2000年后较其它指标的误差结果小，似乎隐含着降水时间分布的主导作用。另外2000年后整体模拟的误差较大，可能还有其它因素的影响。大规模的人类活动对下垫面的影响日益增加，泾河流域建设大量的淤地坝会减少流域径流量，增加实际蒸散量[28]。平凉市政府于2000年开展了泾河河道生态综合治理工程[29]。黄河水土保持生态工程砚瓦川(泾河二级支流)项目区，21世纪以来截至2010年，建设淤地坝10座，涝池120座，水窖3 444眼，沟头防护117处，谷坊1 957道[30]。这些人类活动对下垫面状况造成了一定的影响，进而影响到流域的水量平衡过程。

3 结 论

本研究在Budyko-Fu模型下，以泾河流域为例，对3种气候季节性指标(SI1、SI2、SAI)做出对比，并对SAI指标中水热变化时相差的选取进行探讨，区别为SAI1与SAI2两个指标。结果表明，已有的3种气候季节性指标中，若流域降水量与潜在蒸散季节相位由多年平均状况确定，选取平均相位差，由此计算气候季节性指标SAI2，其表现较好。由SAI2和NDVI给出的参数ω的半经验公式的决定系数较高，将之用于Budyko-Fu模型中，能够提高流域年径流量的模拟精度，说明同一流域逐年计算指标SAI时采用多年平均相位差能够更加确切地描述流域的气候季节性特征。期望本研究能为流域水热耦合过程与水量平衡研究及流域节水管理提供参考。