多维磁悬浮隔振系统动力学模型与控制策略

武倩倩＊，崔宁刘碧龙岳洪浩，刘荣强

1.青岛理工大学 机械与汽车工程学院，青岛 2665202.哈尔滨工业大学 机电工程学院，哈尔滨 150001

航天器在轨运行时，动量轮、制冷机等设备会产生一种量级较小、频带较宽的微振动。这类微振动对空间科学实验结果、高分辨率对地观测精度、重力梯度测量精度等均有较大影响［1－4］。当前应用比较广泛的被动隔振系统对高频振动具有较好的隔振控制效果，但对低频振动控制效果不佳［5－6］。磁悬浮隔振技术能利用磁场与电场产生的洛伦兹力实现空间微振动的隔离与抑制，对低至0.01Hz的微振动仍有良好的隔振效果，在空间微振动隔振领域具有广阔的应用前景［7－9］。

磁悬浮隔振系统具有非线性、强耦合、高响应、宽频带等特点，并且系统的控制目标与定子和浮子之间的相对位置存在制约关系，这均增加了系统低频隔振控制的难度。为了实现隔振控制，国内外学者采用经典控制方法和现代控制方法开展了大量的研究。Tryggvason［10－11］和 Fenn［12］等以扩大控制带宽为目的设计了PID控制器，但未考虑以多自由度系统动力学模型为研究对象的控制响应。Zhu等［13］在此基础上采用PID型双积分加速度控制方法，增加了系统隔振频带，提高了系统的隔振性能，但其仅对单自由度隔振系统进行了控制仿真。Hu等［14］采用串级PID控制算法对一种磁悬浮作动器进行隔振控制，但也未研究由多个作动器驱动的多自由度隔振系统的控制响应。Liu等［15］分别采用经典PID控制算法和H∞控制算法对整柜级磁悬浮隔振系统进行了控制仿真，仿真结果表明两种算法都有良好的隔振效果，但尚缺少实验验证。Li等［16］基于改进的FXLMS（Filtered-X Least-Mean-Square）算法对非线性磁悬浮作动器进行了自适应控制，该算法对作动器的非线性有良好的补偿特性，但未涉及多自由度隔振系统的非线性控制特性。Yang等［17］考虑到参数化和动态不确定性的特点，针对微重力隔振系统g-LIMIT（Glovebox Integrated Microgravity Isolation Technology）设计了一种自适应性控制器，在高频增益加速度环和低频相对位置环内加入两个神经网络，阻止了自适应控制过程中加速度环与位置环的相互作用，但文中也仅研究了单自由度隔振系统的仿真结果。Hampton等［18］将最优前馈与后馈控制方法应用到 MIM （Microgravity vibration Isolation Mount）微振动隔振系统中，也仅在单自由度隔振模型上实现了较好的控制效果。综上可知，当前研究大多是在简化的单自由度模型基础上进行的，缺少针对六自由度磁悬浮隔振系统的高精度非线性动力学建模以及基于模型的控制策略设计与控制系统仿真。

针对上述问题，本文首先以定子和浮子之间的相对位姿为变量，建立了面向控制的六自由度磁悬浮隔振系统非线性动力学模型；其次，针对系统的非线性、强耦合、宽频带特性，设计了双闭环控制策略，并利用PD定点控制算法，仿真了系统在不同频带内的隔振性能与跟踪性能；最后，搭建了磁悬浮隔振样机测试系统，对建立的系统动力学模型和提出的控制策略进行验证。

1 磁悬浮隔振平台的工作原理

磁悬浮隔振平台由定子、浮子、线缆和洛伦兹力作动器组成，如图1所示。作动器包含两组条形永磁体、矩形空心线圈以及磁轭。每个洛伦兹力作动器具有1个自由度，为了实现空间6自由度的微振动隔振，采用8个作动器均布于定子与浮子之间，通过改变作动器的位姿，使8个作动器可以解算六自由度的控制力和控制力矩。当定子受到外界扰动时，通过调节线圈电流的大小和方向使作动器产生能抵消外部扰动的洛伦兹力，从而为浮子上的有效载荷提供准静环境。为避免浮子与定子在隔振频带内发生碰撞，设计时要求控制行程大于隔振频带内的最大振幅。为避免由于瞬态扰动产生幅值过大的情况，在浮子和定子之间设计限位机构。基于上述工作原理，设计了控制行程为±3mm的6自由度磁悬浮隔振平台，其三维模型及尺寸参数如图2所示。

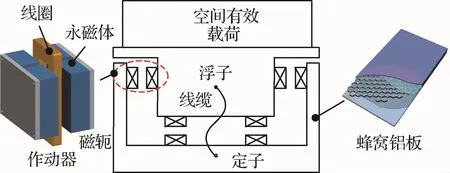
图1 磁悬浮隔振平台示意图Fig.1 Diagram of maglev vibration isolation platform

图2 磁悬浮隔振平台三维模型Fig.2 Three-dimentional model of maglev vibration isolation platform

2 多维磁悬浮隔振系统动力学建模

高精度的系统动力学模型是实现隔振控制的前提。为保证模型精度，以浮子和定子之间的相对位姿为变量，建立面向控制的6自由度系统动力学方程［19－22］。系统空间几何模型如图3所示，其中NIJK为与地面固联的惯性坐标系，S为与定子固联的坐标系，Fijk为与浮子固联的坐标系。定子坐标系的坐标原点位于定子质心，浮子坐标系的坐标原点距离其质心的位置矢量为rc。假设在初始状态下，定子坐标系与惯性坐标系重合，定子坐标系到浮子坐标系的位置矢量为RSF。根据牛顿-欧拉方程，浮子的力和力矩方程为

图3 系统空间几何模型Fig.3 Space geometry model for system

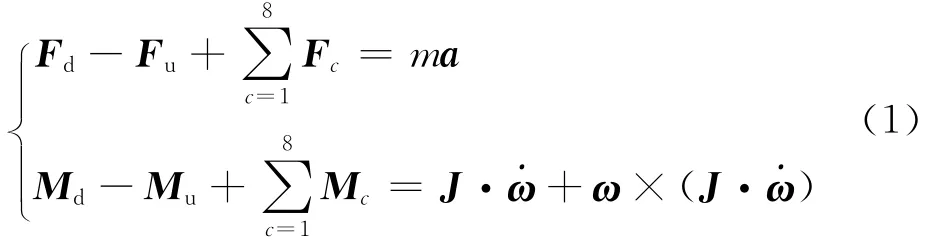
式中：m为浮子本体与有效载荷的总质量；J为浮子的惯量张量；Fd为直接作用于浮子上的外力；Fu为线缆产生的扰动力；Fc（c＝1，2，…，8）为主动控制力；Md为浮子上作用的外力矩；Mu为线缆产生的扰动力矩；Mc（c＝1，2，…，8）为主动控制力矩；a为浮子的绝对加速度；ω为浮子的角速度。

根据欧拉角和坐标系的转换方式，可得惯性坐标系到浮子坐标系之间的转换矩阵Γ为

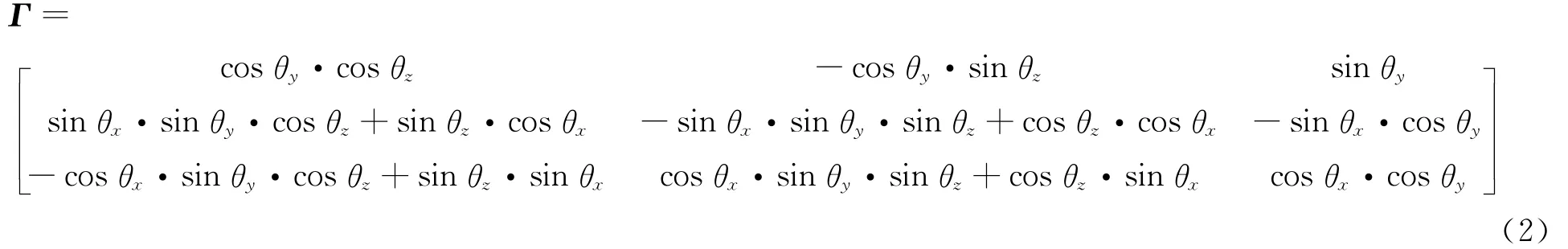
式中：θx、θy、θz为浮子相对定子的横滚、俯仰、偏航运动姿态。

定义空间列阵X＝ ［x y z θxθyθz］T，其中r＝［x y z］T表示浮子与定子之间的相对位移变化，为了描述浮子的绝对运动状态，需要由定子与浮子之间的相对运动状态加上定子的绝对运动状态得到。由于浮子相对于定子为小角度运动，浮子的角速度量级约10－4～10－3rad／s，而浮子的加速度量级约10－5～10－3m／s2，基于小角度假设，角速度的平方项或角速度的交叉乘积项可以忽略。另外，忽略定子受到的角位移扰动，假设定子受到3自由度的线位移扰动¨R0，根据系统空间几何模型（图3）以及坐标变换关系，代入状态空间列阵X，得到浮子6自由度运动微分方程为

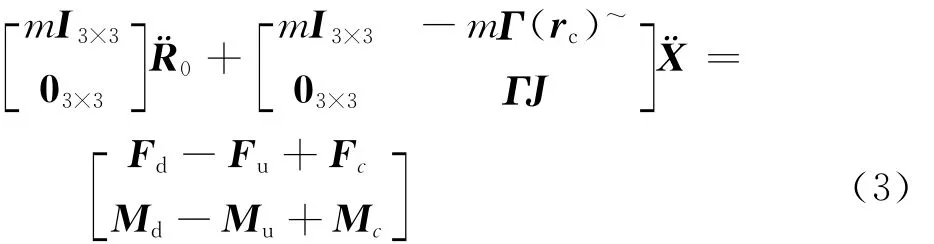
式中：（）～表示括号中向量的反对称矩阵。

定义8个作动器的力向量为

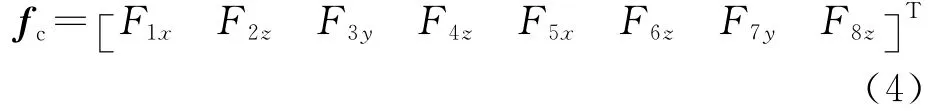
式中：下标中的数字表示作动器的标号，字母表示洛伦兹力的方向。

为了进行矢量叠加，定义洛伦兹力的方向矩阵为

利用坐标系之间的变换矩阵Γ，任意浮子坐标系中的向量q都可以转换为惯性坐标系中的向量，即建模时变量均统一转换到惯性坐标系中。

8个作动器作用于浮子的合力在惯性系中可以表示为

式中：I1＝I2＝…I8＝I3×3。

定义浮子坐标系下作动器的质心到浮子质心的位置矢量为rFcM（c＝1，2，…，8），则作动器的合力对浮子质心产生的力矩为

把浮子与定子之间的两组主要连接线缆等效为弹簧和阻尼系统，定义线缆的刚度系数为Kui（i＝1，2），阻尼系数为Cui（i＝1，2），浮子上线缆接口的位置向量为rui（i＝1，2），定子上线缆接口的位置向量为Rui（i＝1，2），线缆的原始长度为d0i（i＝1，2），变形量为dui（i＝1，2），则

线缆产生的扰动力为

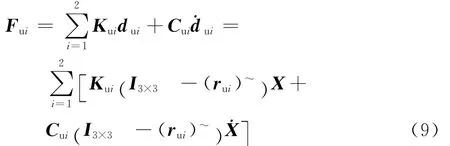
线缆产生的扰动力矩为

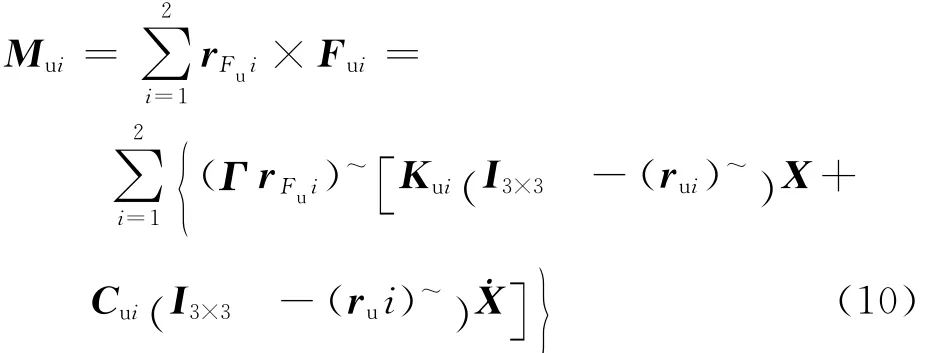
式中：rFui为浮子上线缆作用点到浮子质心的位置向量。

假设外部扰动力fd直接作用于浮子，并且距离质心rd，浮动平台上外力作用点到平台质心的位置向量为rFd，则扰动力和扰动力矩在惯性坐标系中可以写成

把式（6）、式（7）、式（9）～式（12）代入式（3），最终得到面向控制的6自由度磁悬浮隔振系统非线性动力学模型为

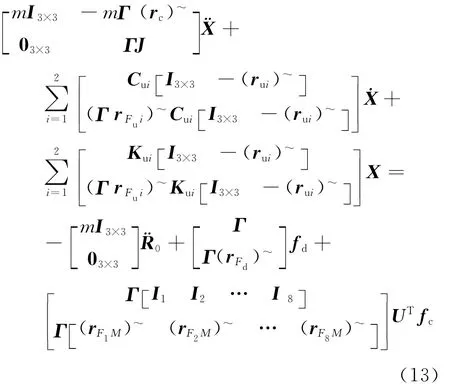
定义以下参数：

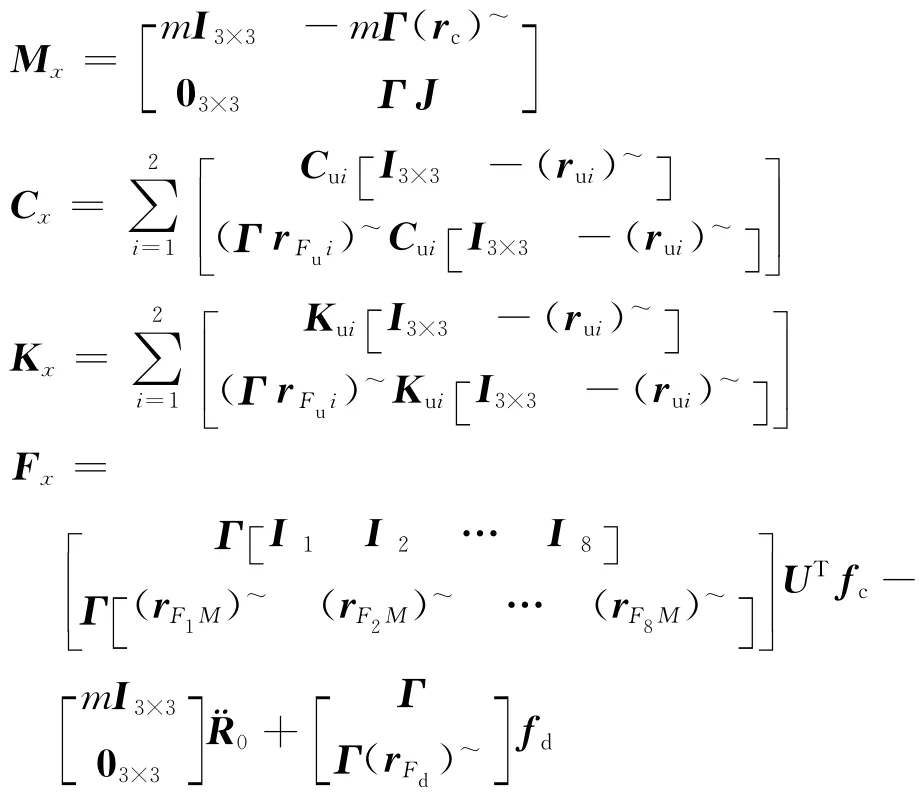
式（13）可写成通用运动微分方程的形式：

3 控制策略设计与控制仿真分析

磁悬浮隔振系统不仅要隔离来自定子的扰动，还要满足浮子与定子之间的位置约束。因此，对磁悬浮隔振系统实施控制时需考虑两个方面：① 使传递到浮子的振动最小；② 使浮子与定子之间的相对位姿保持不变。为实现上述控制要求，设计了包含相对运动状态环和绝对运动状态环的双闭环控制策略，其中相对运动状态控制器的设计原则是在低于隔振频带内实现浮子的运动跟踪，而绝对运动状态控制器的设计原则是在隔振频带内对扰动进行抑制。磁悬浮隔振系统双闭环控制策略框图如图4所示。

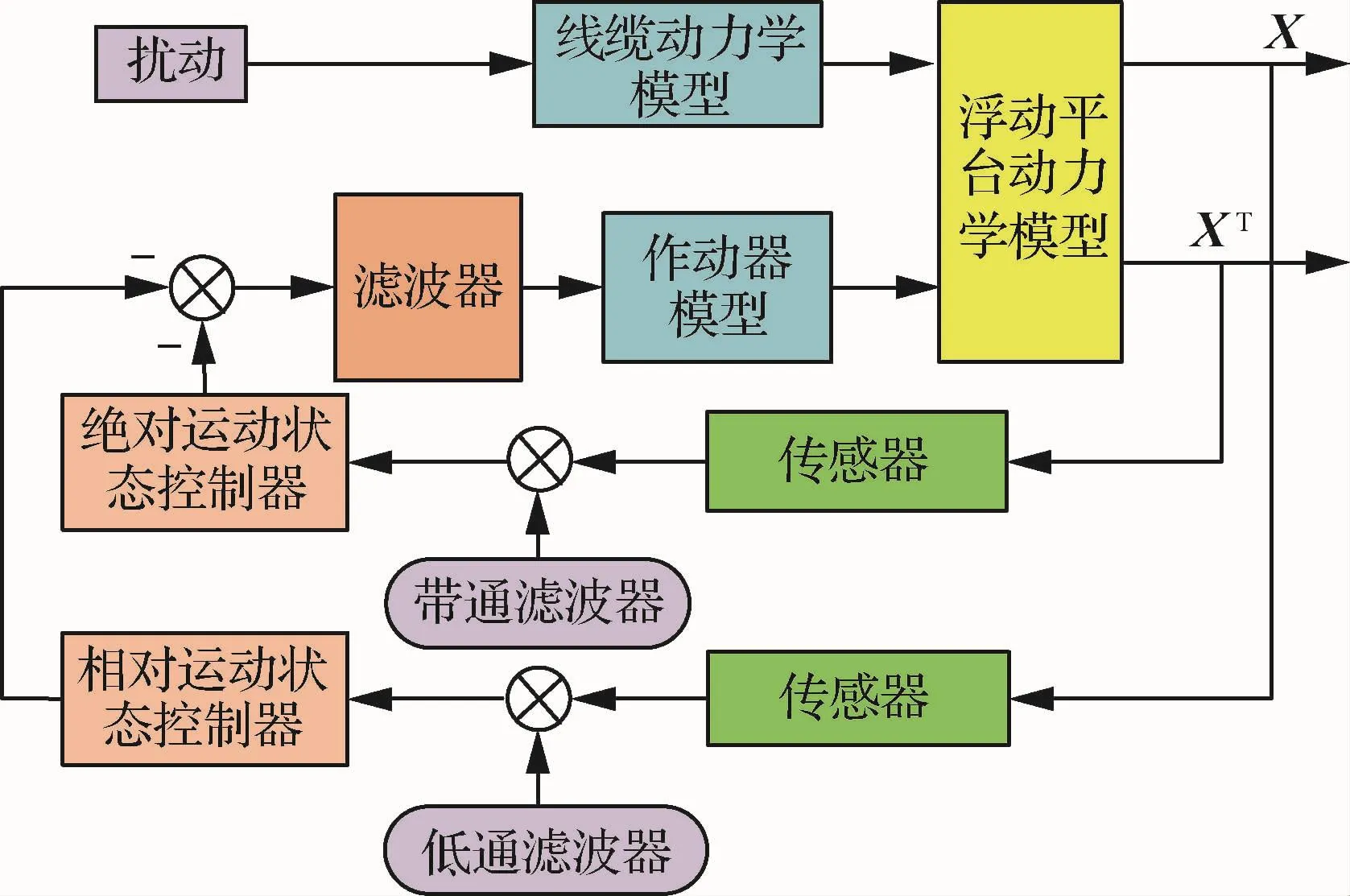
图4 双闭环控制策略框图Fig.4 Block diagram of double-closed-loop control strategy

以0.01～100Hz频带内的振动为研究对象，为了实现0.01～100Hz频带内的隔振控制，设置浮子的绝对速度、绝对加速度目标为0，设置绝对位移目标为与系统初始参数有关的常量。当振动频率低于0.01Hz时，设置定子与浮子的相对速度、相对加速度目标为0，设置相对位移目标为与系统初始参数有关的常量，实现跟踪控制。在建立的6自由度系统动力学模型的基础上，采用PD定点控制方法，在 MATLAB／Simulink环境下，开发6自由度磁悬浮隔振系统控制仿真程序，获得系统在不同频带内的隔振效果与跟踪效果。

3.1 PD定点控制器设计

取ea＝X0Λ－XΛ（上标Λ表示在绝对坐标系下的变量）为隔振前后的绝对位移误差，速度误差和加速度误差分别是为常量。

为了便于分析，把扰动写为6×1的矩阵形式，则位移扰动为R0＝ ［R003×1］T，速度扰动为 R0＝ ［R003×1］T，加 速 度 扰 动 为 ¨R0＝［¨R003×1］T。根据绝对变量与相对变量之间的关系得到

把式（15）代入式（14）可得

式中：KxXΛ0是一个常量，可以通过调节控制参数补偿该常量，因此式（17）可以写成

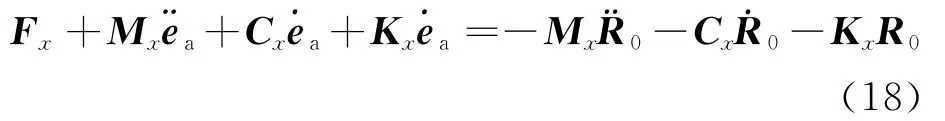
其中：Fx包括主动控制力Fa和外部扰动力Fd。

定义控制规律为

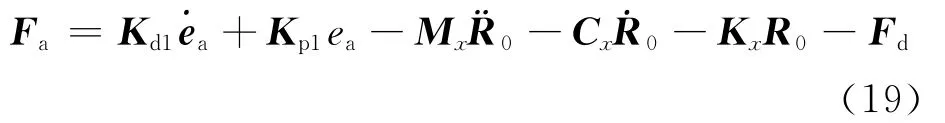
式中：Kp1和Kd1分别为比例控制系数和微分控制系数。

则式（16）可以简化为

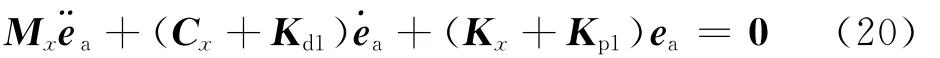
取Lyapunov函数为

由Mx和Kp1的正定性可知，V全局正定，则

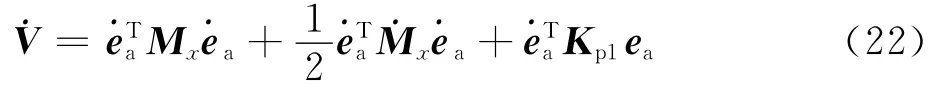
由式（20）和式（22）可得

隔振控制需要满足阻尼比大于1，则Cx＋Kd1正定，此时有V≤0，即系统可达到稳定。当V≡0时，有ea≡0，从而¨ea≡0，ea≡0，所以控制也是收敛的。

为了实现低频运动跟踪，取ep＝X0－X为隔振前后的相对位移误差，则速度误差和加速度误差 分别为ep＝ X0－X，¨ep＝ ¨X0－¨X，其 中 ¨X0＝［00 … 0］T，则运动微分方程可以转换为

定义控制规律为

式中：Kp2和Kd2分别为比例控制系数和微分控制系数。控制系统的稳定性和收敛性证明同上。

3.2 控制仿真分析

根据图2所示的磁悬浮隔振平台三维模型，获得仿真所需的系统参数如表1所示。此外，浮子的转动惯量张量为

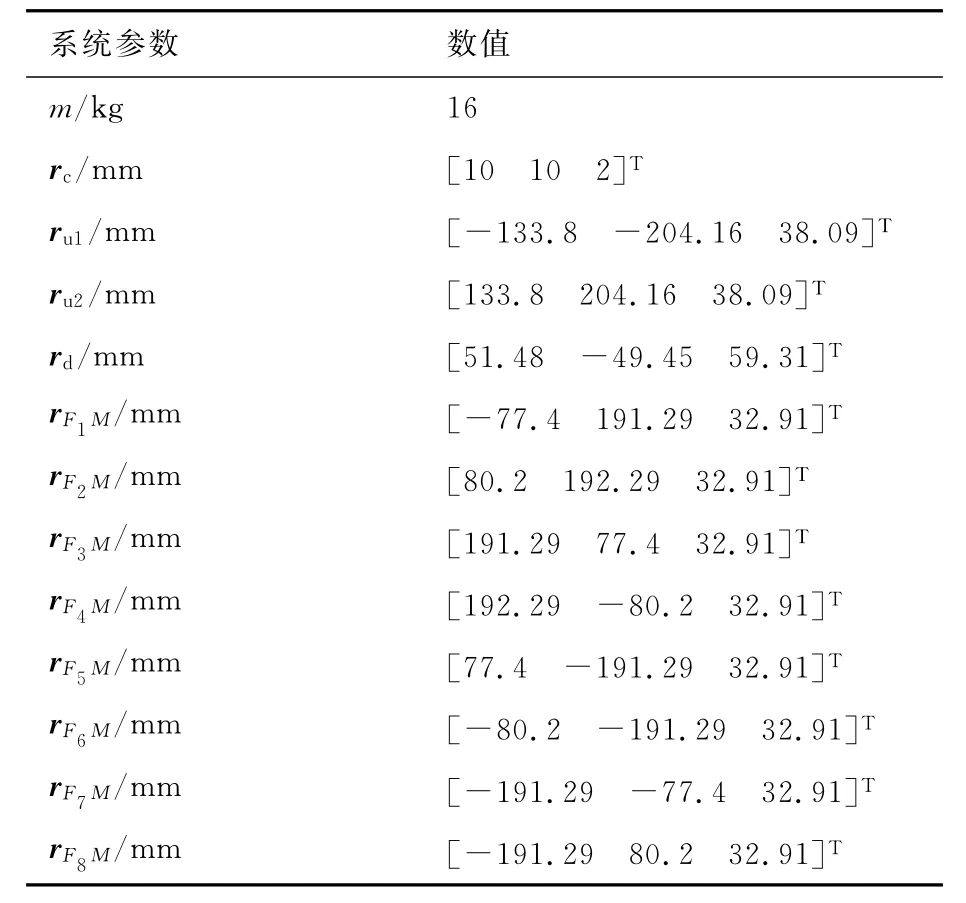
表1 磁悬浮隔振平台系统参数Table 1 System parameters of maglev vibration isolation platform

对磁悬浮隔振系统中的连接线缆进行参数辨识，线缆的刚度矩阵和阻尼矩阵可近似等效为［13］

为了简化运算过程，假设定子受到的扰动为正弦扰动，忽略直接作用在浮子上的外力。给定子施加沿水平轴x方向，幅值分别为2mm、2mm、2μm，频率分别为0.005、0.01、100Hz的正弦扰动，得到了系统的6自由度控制仿真结果。下面以系统沿着x方向和绕着x方向的隔振控制仿真结果（图5、图6）和跟踪控制仿真结果（图7）为例进行说明。

由图5和图6可知，当频率分别为0.01Hz和100Hz时，浮子的绝对位移、速度、加速度以及绝对角度、角速度、角加速度均在短时间迅速收敛至0，表明系统具有良好的隔振控制效果。由图7可以看出，当频率为0.005Hz时，浮子与定子之间的相对位移、速度、加速度以及相对角度、角速度、角加速度也迅速收敛至0，表明系统具有良好的跟踪控制效果。

图5 0.01Hz时有／无控制隔振性能对比Fig.5 Comparison of vibration isolation performance with and without control at 0.01Hz

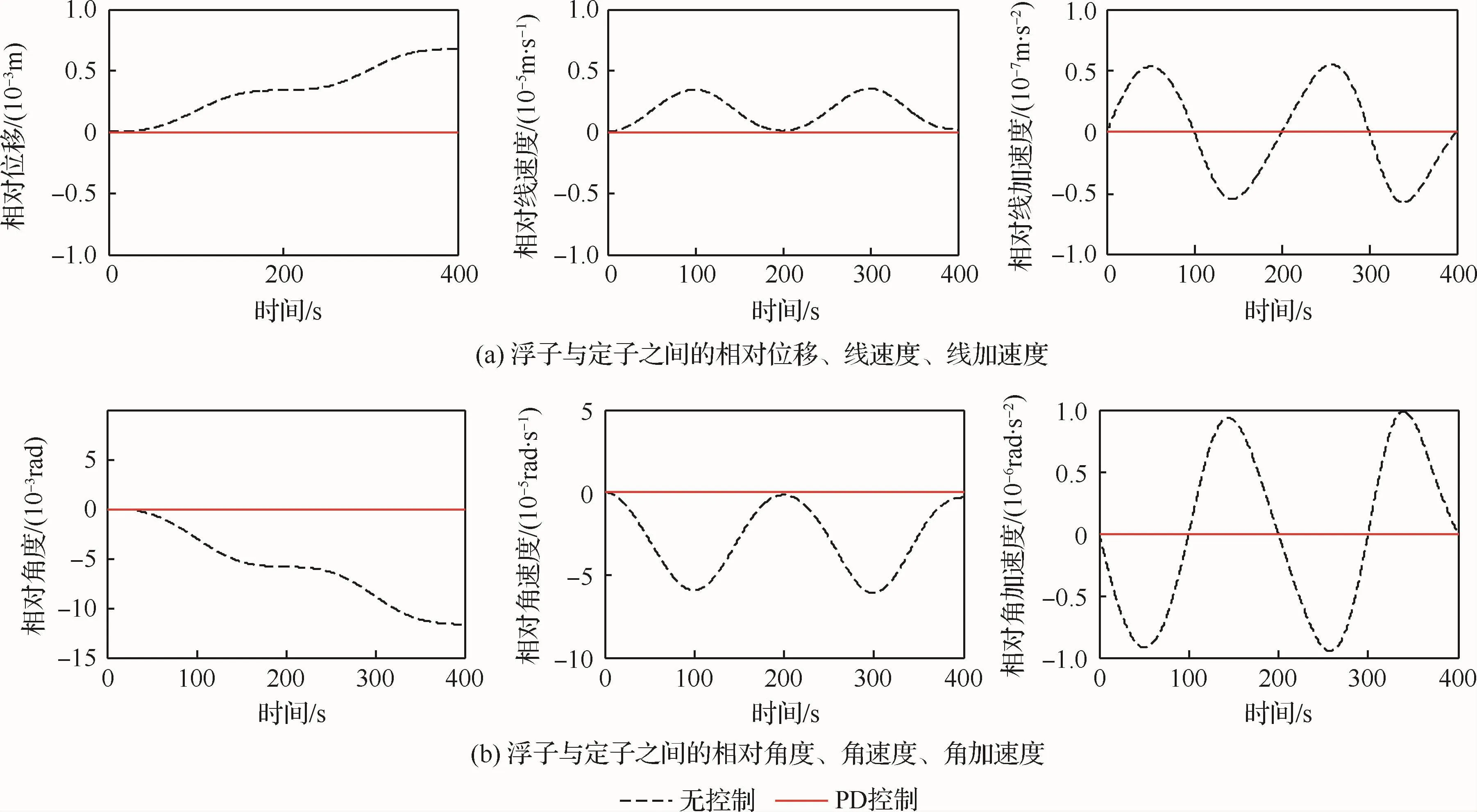
图7 0.005Hz时有／无控制跟踪性能对比Fig.7 Comparison of tracking performance with and without control at 0.005Hz

由上述仿真结果可知，设计的控制策略是有效的。通过仿真结果验证了系统在低频带到高频带内的隔振功能，以及系统在极低频带内的跟踪功能，满足磁悬浮隔振系统的设计要求。

4 磁悬浮隔振系统样机隔振功能试验

研制磁悬浮隔振系统原理样机，搭建如图8所示的试验系统。为获取样机定子受到的扰动参数以及浮子受到的外部作用力，在定子和浮子上分别安装3个三维加速度传感器，在定子和浮子之间安装4个二维相对位置传感器。其中，加速度传感器选用Silicon Design的Model2422，相对位置传感器选用DL400-7-PCBA。驱动器选用Trust Automation的TA115。数据采集、处理及控制软件在 WinCE系统下利用EVC4.0编写，通过数据采集卡提供C接口控制A／D卡（阿尔泰科技的 ART2153）和D／A卡（阿尔泰科技的ART2003），实现传感器数据的采集和控制信号的输出，并在处理器ARM8019中进行滤波处理。设置振动台产生沿水平方向的正弦振动，将磁悬浮隔振系统样机的定子固定在振动台上，分别提取定子和浮子的加速度信息和相对位移信息。振动的加速度频谱分析结果如图9所示（图中g为重力加速度）。由图9可知，该正弦振动频率主要包含5.4、16.22、26.93、37.74、48.55和59.36Hz等多个主频成分以及多个干扰频带。根据提出的双闭环控制策略，采用PD定点控制算法，分别从时域和频域对比控制前后浮子的加速度水平，验证系统的隔振功能。

控制后浮子上沿着振动方向的加速度与扰动加速度对比如图10所示。取相同时间段内扰动加速度峰-峰值（147.82×10－3g）与隔振控制后稳态响 应峰-峰值（9.53×10－3g）进行对比，结果表明系统在振动方向上的隔振百分比可达93.5%，验证了系统的隔振功能。

图8 样机隔振功能测试Fig.8 Vibration isolation performance test of prototype

隔振控制后浮子的加速度与扰动加速度频谱分析结果如图11所示，在0～70Hz频带范围内，不同频率的扰动都得到了有效抑制。

图9 振动的加速度频谱Fig.9 Acceleration spectrum of vibration

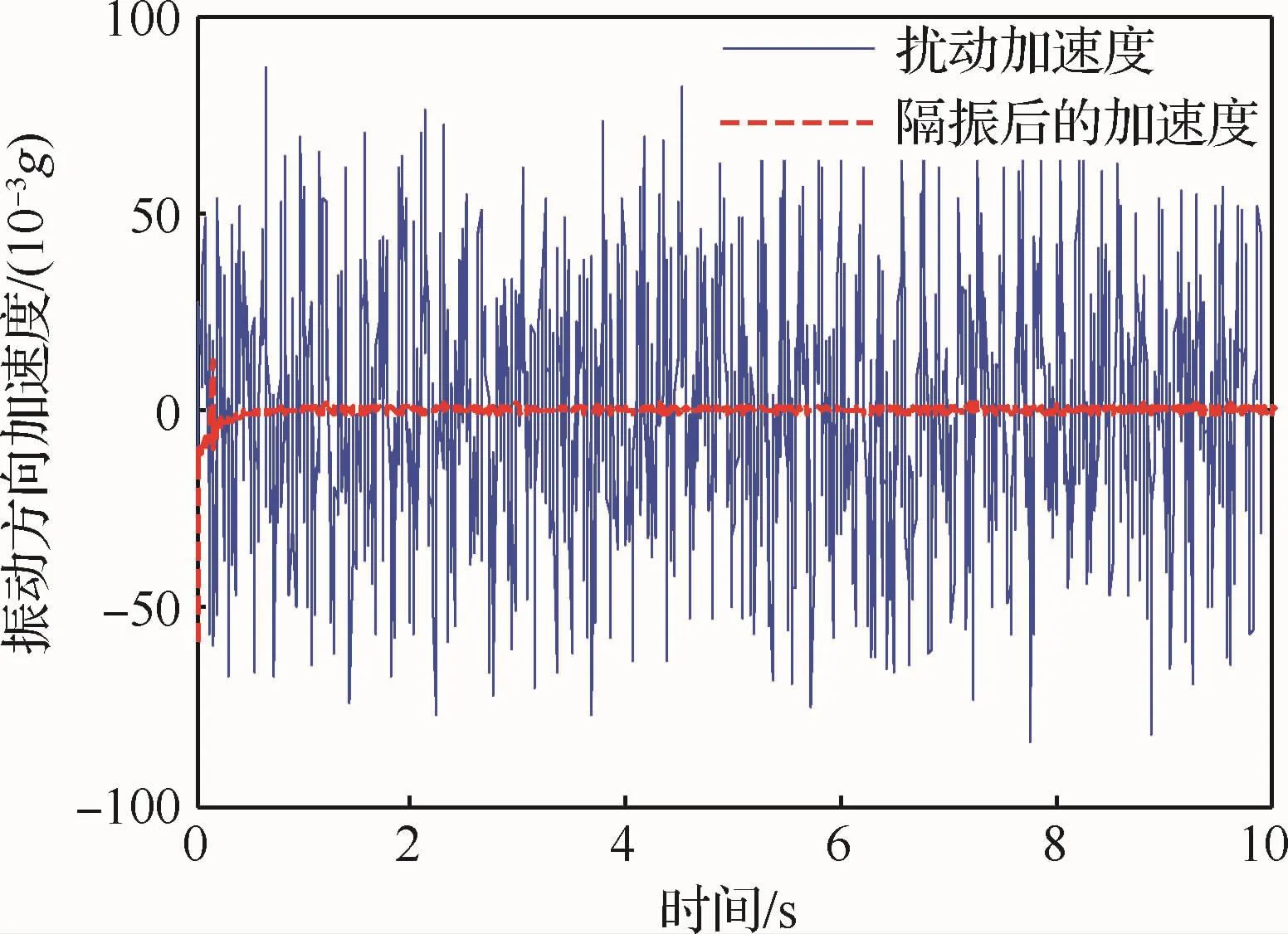
图10 沿着振动方向的加速度测试结果Fig.10 Test results of acceleration along vibration direction

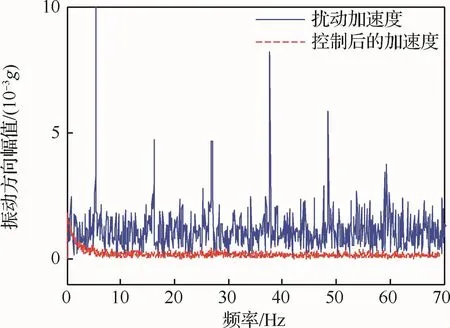
图11 控制前后频域结果对比Fig.11 Comparison of frequency domain results before and after control

把测试得到的扰动加速度作为输入添加到仿真程序中，在相同控制参数的作用下，获得基于系统动力学模型的控制仿真结果，并与实际测试结果对比，如图12所示。结果表明，基于仿真模型获得的加速度控制响应与实际模型的响应趋势一致，验证了系统动力学模型的正确性。

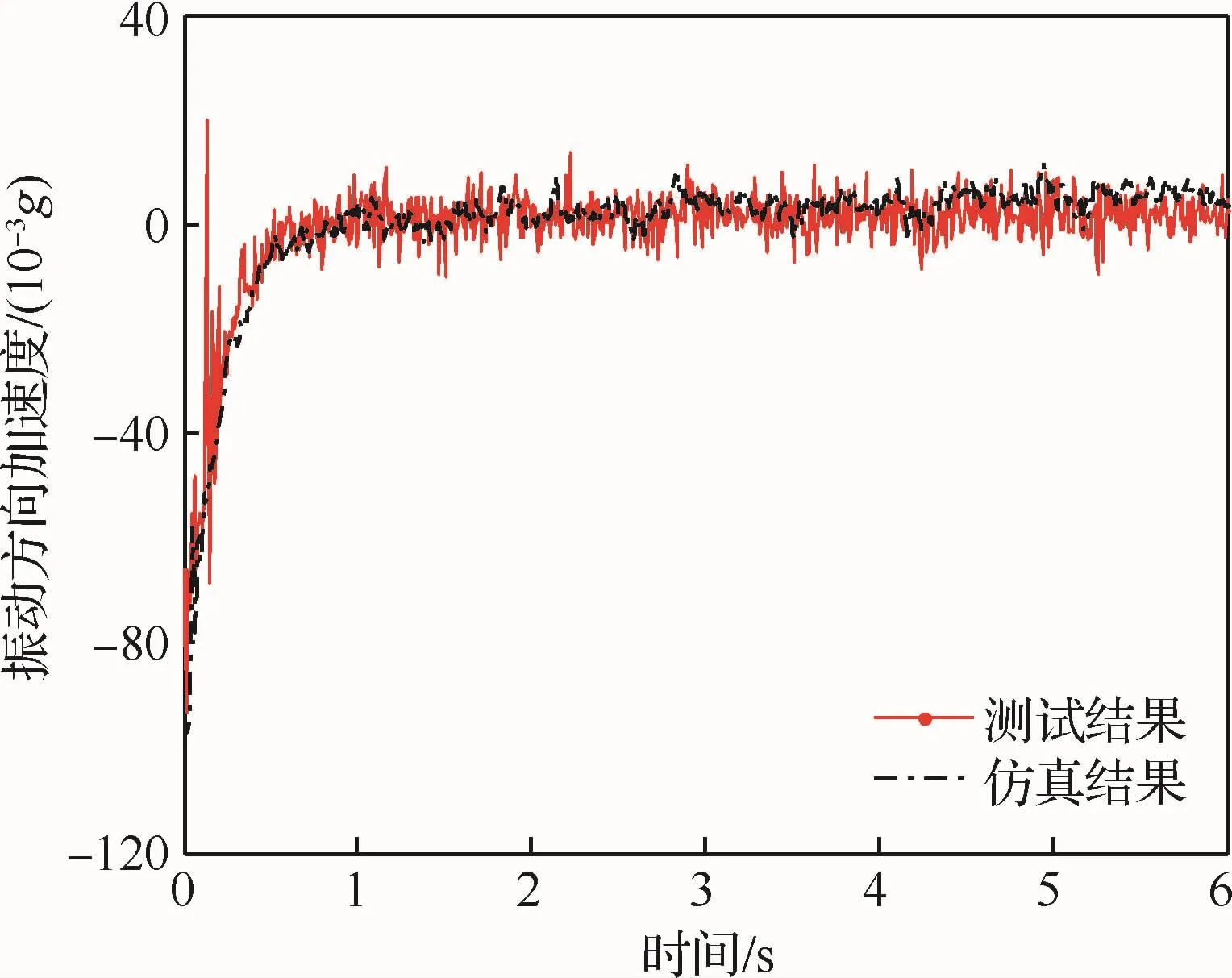
图12 模型仿真结果与测试结果对比Fig.12 Comparison of simulation results and test results of model

5 结 论

1）为提高控制精度，获得高保真的控制响应，基于牛顿-欧拉方程，建立了面向控制的6自由度磁悬浮隔振系统非线性动力学模型。

2）针对低中频带内的隔振控制目标和极低频带内的跟踪控制目标，设计了包含相对运动状态环和绝对运动状态环的双闭环控制策略。

3）在MATLAB／Simulink环境中开发了控制系统仿真程序，采用PD定点控制算法，通过隔振控制仿真和跟踪控制仿真，表明系统在隔振频带内具有良好的隔振效果，在极低频带内具有良好的跟踪效果，验证了控制策略的有效性。

4）研制了磁悬浮隔振系统样机，搭建了样机试验系统，通过试验测试，系统沿振动方向的隔振百分比可达93.5%；频域响应结果表明系统能有效抑制0～70Hz频带内的扰动。通过对比测试结果与仿真结果，验证了系统动力学模型的正确性。

在未来的研究中，拟建立多自由度振动激励系统，验证磁悬浮隔振系统在多自由度扰动耦合作用下的隔振性能。