基于LADRC的舰载V／STOL飞机短距起飞性能优化

吴文海，高阳，王子健，周思羽

海军航空大学青岛校区 控制工程与指挥系，青岛 266041

垂直／短距起降（Vertical and／or Short Take-Off and Landing，V／STOL）飞机是对垂直起降（Vertical Take-Off and Landing，VTOL）和短距起飞／垂直降落（Short Take-Off and Vertical Landing，STOVL）固定翼飞机的统称，它兼具旋翼和固定翼飞机的优势，既可以减少甚至摆脱对飞行跑道的依赖，又具备较大的飞行速度、航程、载荷和优异的机动性能。自20世纪40年代至今，诞生的各类 V／STOL 飞机型号达30余种［1－2］。特别是近年来，随着美国第五代战斗机F-35B的研发和服役，关于V／STOL飞机的研究越来越重视。然而，由于V／STOL飞机采用了诸多的推力矢量装置，如单发四转向喷管、矢量尾喷管、引射增升器、升力风扇等，使其相比常规起降飞机具有了更为复杂的动力学特性［3］和操控性［4］。其中，短距起飞是依靠推力矢量实现的典型非常规飞行模式，亦是舰载V／STOL飞机能否在有限的甲板上完成自主起飞的首要性能指标。对于舰载短距起飞性能，首先期望舰面滑跑距离最短，这样即可以在有限的甲板长度内实现最大的起飞质量；其次期望离舰爬升性能优良，使之能快速而稳定地转入平飞模式。因此，开展短距起飞性能优化研究有其必要性和实际意义。

对此，国内外学者从不同的角度开展了一定的研究工作。文献［5］比较了不同动力方案对起飞滑跑距离的影响，结果表明，采用“矢量尾喷管＋升力风扇”方案可大大缩短滑跑距离，分别仅为单矢量喷管方案和无推力矢量方案的41.6%和19.7%。文献［6］则利用文献［7］针对“鹞”式飞机的爬升高度所提出的遗传算法优化策略，以滑跑距离为目标函数，给出了倾转旋翼机的动力短舱角与起飞质量的最佳匹配关系。然而，上述文献只研究了单推力矢量对短距起飞性能的影响，并没有考虑多推力矢量的协调操纵优化问题，而且忽略了对离舰后爬升性能的优化控制，因而存在一定的局限性。对此，目前鲜有文献研究V／STOL飞机甚至是推力矢量飞机的起飞控制问题。根据文献［8-9］的描述，当 V／STOL飞机处于爬升状态时，由于具备了一定的空速，为节省燃料消耗、提高控制效能，通常不采用推力矢量而直接利用气动舵面（升降舵、鸭翼等）进行操控。其中，利用经典的PID控制飞机的俯仰角、爬升速度或高度是最常见的控制策略［9－11］。此外，文献［12-13］分别给出了基于动态逆控制和自适应控制的爬升高度跟踪策略。但总体而言，现有研究所设计的各类爬升控制器，大多没有充分考虑鲁棒性的问题，即对于不同性质、不同强度的干扰因素难以有效克服。

对此，韩京清研究员于20世纪90年代提出了一种自抗扰控制（Active Disturbance Rejection Control，ADRC）策 略［14］。大 量 理 论［15－17］和 应用［18－19］方面的研究表明，ADRC不依赖被控对象的精确数学模型，对具有未建模动态、参数摄动和外界干扰的系统均能实施有效控制，具有“天生”的鲁棒性和抗干扰性。但受限于原始ADRC中非线性、非光滑的反馈结构，其理论分析较为困难，在应用中需要调节的控制器参数也较多。为简化ADRC的分析和实现，作者在文献［20］中基于单参数高增益观测器思想，提出了一种高阶线性ADRC（Linear ADRC，LADRC）方法，并放宽文献［21］的假设条件给出了收敛性证明。

本文在上述研究成果的基础上，考虑舰载V／STOL飞机在整个短距起飞过程中的实际需求和操控特性，首先建立了反映各起飞阶段动力学特性的非线性模型。然后给出了舰面滑跑和离舰初期的预置推力偏转方案，以分别实现舰面滑跑距离最短和离舰后增速时间最短。在此基础上为提高离舰中期的爬升速度，提出了一种线性自抗扰反演（LADRC-Backstepping）控制方法，实现了对爬升角非仿射系统的有效控制；之后，直接利用高阶LADRC方法设计了俯仰角控制器，最终使V／STOL飞机以稳定的姿态爬升。最后，数值仿真验证了本文所提出的优化操控策略的有效性和优越性。

1 短距起飞动力学建模

本文研究的V／STOL飞机为美国NASA某型STOVL验证机［8］，采用单发动机、三角翼、鸭翼、双垂尾的布局形式，推进系统采用类似F-35B的设计方案，由一个轴驱动升力风扇和一个矢量发动机组成，如图1所示。其中，矢量尾喷管在飞机对称平面内可向下偏转90°（下偏为正），升力风扇竖直安装于驾驶舱后方，可向前偏转20°、向后偏转60°（后偏为正），通过两者之间推力的转换以及各自在对称平面内的偏转，可实现飞机纵法向的推力矢量控制。此外，尾喷管和升力风扇还可侧向偏转±12°，连同位于左、右翼根处的两个滚转控制喷管，可实现飞机横侧向的推力矢量控制。

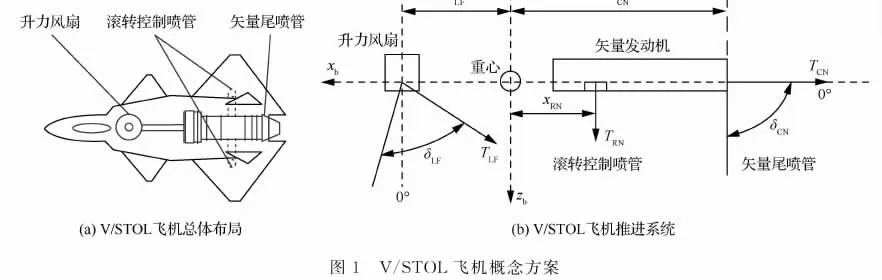
Fig.1 Conceptual scheme of V／STOL aircraft

参考F-35B短距起飞的影像资料，本文以“黄蜂”级两栖攻击舰为搭载平台，其直通飞行甲板长为250m，起飞跑道长为160～180m，即要求上述V／STOL飞机在此范围内能够离舰起飞。

对此，根据V／STOL飞机在短距起飞过程中受力和运动状态的不同，可将整个过程分为3个阶段：三轮滑跑、抬起前轮滑跑和离舰爬升。由于起飞过程主要涉及纵向动力学的变化，故下面利用三自由度系统的纵向动力学方程描述V／STOL飞机在短距起飞模式下的运动［22］。

1.1 三轮滑跑段

在三轮滑跑段，飞机的高度和俯仰姿态几乎不变，滑行速度与平直甲板平行，因此有如下近似条件：h ＝wg＝0，V ＝ug，θ＝q＝0，γ＝0，α＝θ＝θs，θs＝1.12°为停机角。结合此阶段飞机的受力情况（如图2所示），可得纵向运动方程为（其中规定推力T、支持力N和摩擦力f为正值，相应力臂为矢量）

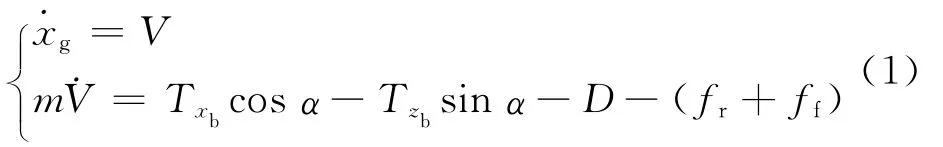
以及法向力和俯仰力矩平衡方程：

式中：推进系统产生的纵向力Txb、法向力Tzb和俯仰力矩mprop分别为

气动阻力D、升力L和俯仰力矩maero分别为

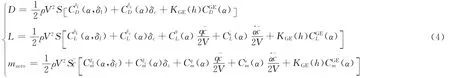
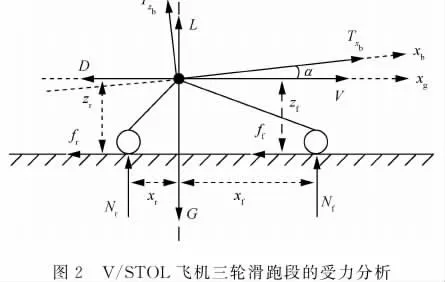
Fig.2 Force analysis of V／STOL aircraft in the three wheel taxiing stage

式中：TCN、TLF、TRN分别为尾喷管、升力风扇和滚转控制喷管的推力；δCN、δLF分别为尾喷管和升力风扇的纵向偏转角；Nf、Nr、ff、fr分别为甲板对前轮和主轮的支持力和摩擦力，且有ff＝μNf、fr＝μNr，μ＝0.01为摩擦系数；δf、δc分别为襟翼和鸭翼偏转角；α为迎角；θ为俯仰角；q为俯仰角速度；γ为爬升角（航迹倾斜角）；V为飞行速度；xg为飞行距离；h为飞行高度；m为飞机起飞质量；ρ为空气密度；S为机翼面积；珋c为平均气动弦长；KGE（h）为地面效应洗出因子；CGED（α）、CGEL（α）、CGEm（α）分别为地面效应诱导阻力、升力和俯仰力矩系数。

1.2 抬起前轮滑跑段

随着V不断增加，Nf逐渐减少，当Nf＝0时，飞机抬起前轮，进入后轮滑跑阶段。此时，V仍平行于跑道，γ＝0，但θ开始增大，q≠0，相应的纵向运动方程为

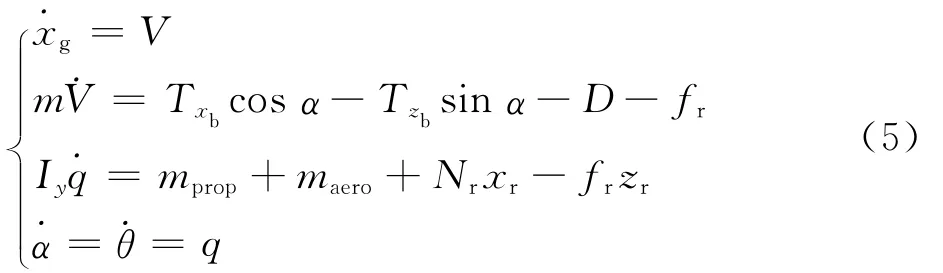
同时有法向力平衡方程

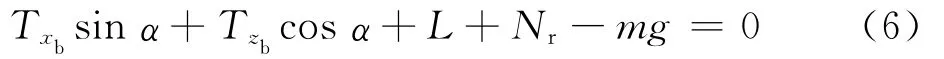
1.3 离舰爬升段

当Nr＝0时，飞机离舰爬升。此时地面效应消失，但由于飞机离地，会使喷射气流受到对面来流的影响而产生喷气诱导效应。该效应实质是由升力风扇和尾喷管向下的喷射流及其之间向上的“喷泉流”引起的，其大小主要与喷管的大小、偏转角度、射流速度及飞机的飞行速度和高度等因素有关，但总体上表现为升力损失并产生抬头力矩。另考虑到V／STOL飞机的推力矢量控制特性，即当V≥75m／s时，可关闭升力风扇并将尾喷管过渡到常规飞行状态，将此阶段的飞机运动模型分为2部分：

当V＜75m／s时（离舰初期），纵向运动方程为

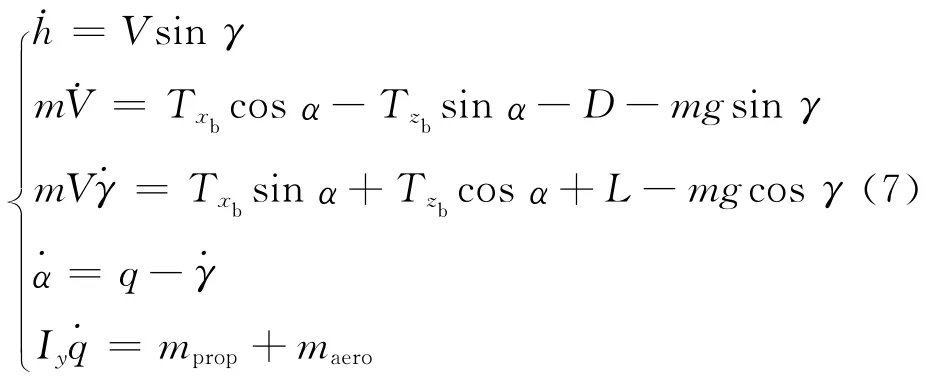
其中，喷气诱导效应模型为

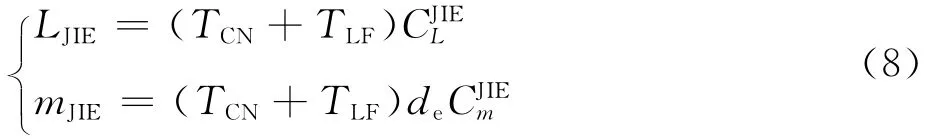
式中：de为总的等效环流喷气直径，表示为de＝，AX（X ∈ ｛LF，CN，FT｝）分别为升力风扇、尾喷管和“喷泉效应”的喷口面积；CJLIE、CJmIE分别为喷气诱导升力和俯仰力矩系数，具体表示为

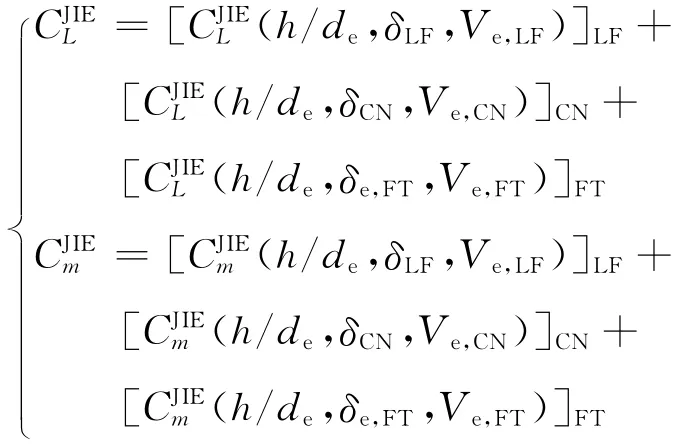
式中：δe，FT＝υδLF＋（1－υ）δCN为等效喷气角，υ＝TLF／T 为推力比；Ve，X（X ∈ ｛LF，CN，FT｝）为相应的等效喷气速度比。这样，在式（4）中去掉地面效应模型并加上式（8）即可得到新的气动力模型。

当V≥75m／s时（离舰中后期），纵向运动方程为

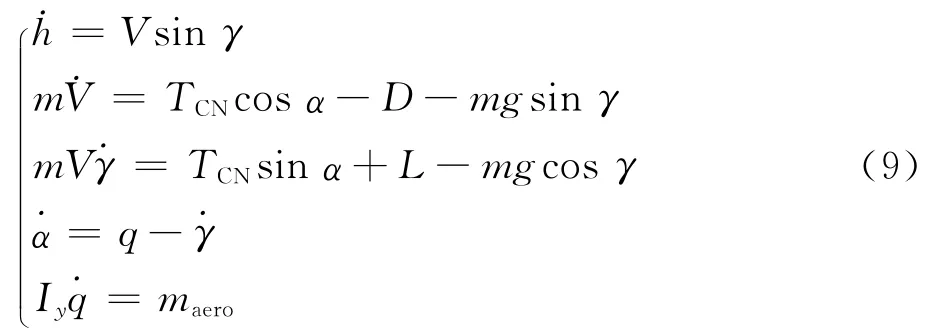
此时喷气诱导效应也消失，式（4）变为常规气动力模型。

2 预置推力偏转角的优化选择

V／STOL飞机能够实现短距起飞，主要依靠推力矢量。但由于其在舰面上加速滑跑的时间很短，飞行员承受的纵向过载很大，这往往使飞行员无法在舰面滑跑和离舰初期操纵飞机；又由于此过程发动机处于全开力状态，为确保短距起飞性能，必须预先设置合理的推力偏转角。为此，本节基于三轮滑跑、抬起前轮滑跑和离舰初期的动力学模型（式（1）～式（8）），给出如下预置多推力偏转优化方案。

2.1 舰面滑跑时的预置推力偏转角

首先，期望V／STOL飞机在舰面上加速滑跑的距离最短。为此，以滑跑距离为性能指标，兼顾考虑离舰速度和迎角，对此阶段尾喷管和升力风扇的预置偏转方案进行优化。

一方面，参考F-35B短距起飞时，其尾喷管向下偏转60°、升力风扇向后倾斜15°，滑跑122m可以实现22 700kg的起飞重量要求；另一方面，考虑V／STOL飞机舰面滑跑时的初速度较小（舰船以一定速度航行相当于飞机对空气具有一定的初速度），为实现短距起飞，在不断加速的同时必须具有一定的Tzb和mprop；因此，选取滑跑时的预置推力偏转角δCN1＝30°，45°，60°、δLF1＝15°，30°，45°进行优化选择。设定两栖攻击舰航速为25kn（1kn＝1.852km／h），即V0＝12.86m／s，h0＝20.35m，m＝22 700kg，δf＝15°、δc＝20°，TCN＝80kN，TLF＝89kN，TRN＝17.33kN，根据式（1）～式（6）即可得到不同推力偏转角下的滑跑距离（Nr＝0时）及其他参数，如表1所示。

从表1可以看出，当δLF1固定不变、δCN1处于中间值45°时或当δCN1固定不变、δLF1处于中间值30°时，相应的滑跑距离最短，且改变δLF1比改变δCN1在缩短滑跑距离上更为显著；虽然在δLF1＝30°时3种方案的滑跑距离相差不大，但在其他指标方面，选择δCN1＝45°有显著优势。原因在于，减小δCN1会使滑跑初期飞机轮胎的载荷显著增加，且离舰迎角较大，容易使飞机在离舰初期达到临界迎角的限制而使飞机性能变差；增大δCN1则会使飞机滑跑的加速度不够而使离舰速度和迎角较小，进而影响飞机离舰后的爬升速度。综合比较，当δCN1＝45°，δLF1＝30°时，舰面滑跑的性能最佳。

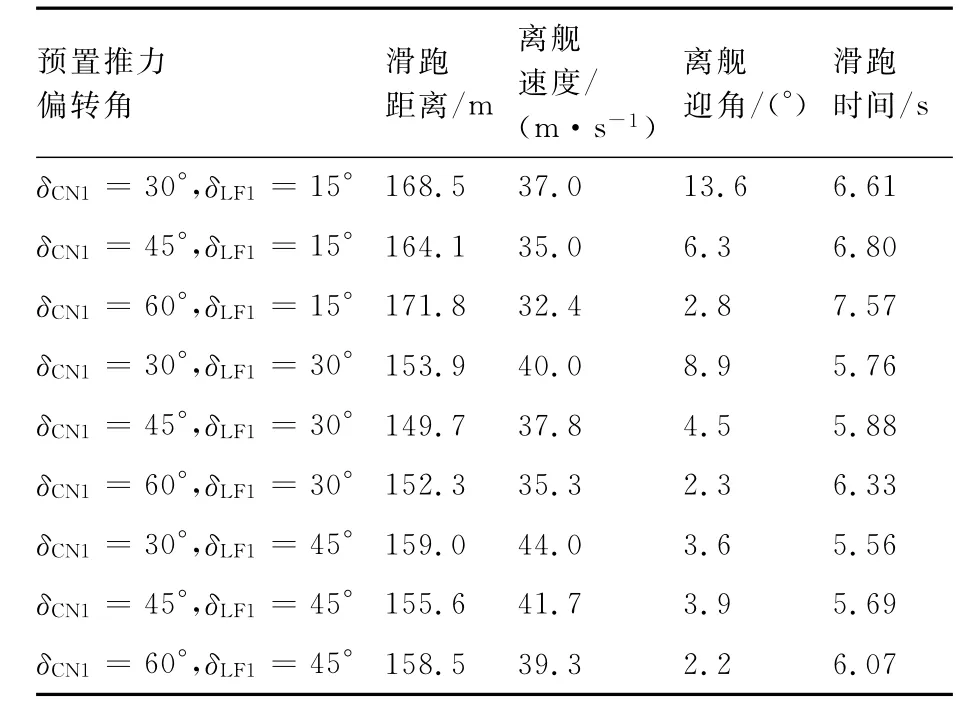
表1 不同推力偏转角下的舰面滑跑性能比较Table 1 Comparison of deck taxiing performance at different thrust deflection angles

2.2 离舰爬升时的预置推力偏转角

继而，期望V／STOL飞机离舰后能尽快增速至75m／s，以转入常规爬升状态。为此，以增速过程所用时间为性能指标，兼顾考虑爬升高度，对离舰初期的预置推力偏转方案进行优化。

鉴于V／STOL飞机离舰时已拥有相当的升力，在此基础上，可通过减小δCN1、增大δLF1来增加前向推力、提高飞行速度。故选取离舰时的预置推力偏转角δCN2＝0°，15°，30°、δLF2＝30°，45°，60°进行组合优化。以离舰状态为初始状态，根据式（7）可以得到V＝75m／s时的爬升性能参数，如表2所示。

从中不难看出，当δLF2＝60°即升力风扇向后偏转最大时可获得较快的增速性能，其中δCN2＝0°和δCN2＝15°时的增速效果几乎一致，但前者的爬升性能相对更优，且尾喷管是直接过渡到常规飞行状态，可避免二次执行过渡操纵，因此选择δCN2＝0°，δLF2＝60°作为离舰时预置推力偏转角。

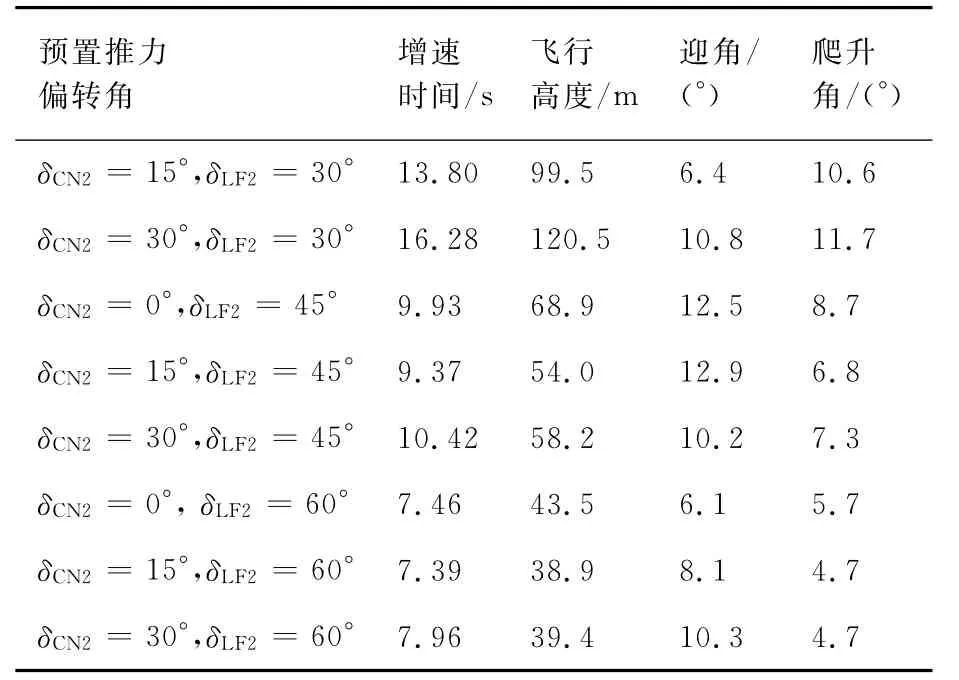
表2 不同推力偏转角下V＝75m／s的爬升性能比较Table 2 Comparison of climbing performance at different thrust deflection angles（V＝75m／s）

3 离舰爬升段控制器设计

在预置推力矢量的操控下飞行速度达到75m／s，此时推力矢量关闭，发动机工作于最大加力状态，V／STOL飞机开始由鸭翼操纵并转为常规爬升模式。为减少燃料消耗、提高爬升性能，期望飞机能以稳定的爬升角尽快升至300m高度；然后收起襟翼，减小发动机功率，再以稳定的俯仰角爬升。因此，需要分段设计爬升角和俯仰角控制器。

3.1 爬升角控制器设计

由式（9）可知，爬升角控制由γ－α－q 子系统决定。该系统是典型的纯反馈非仿射系统，基于自抗扰控制思想［14］可将其转化为如下严反馈仿射形式：

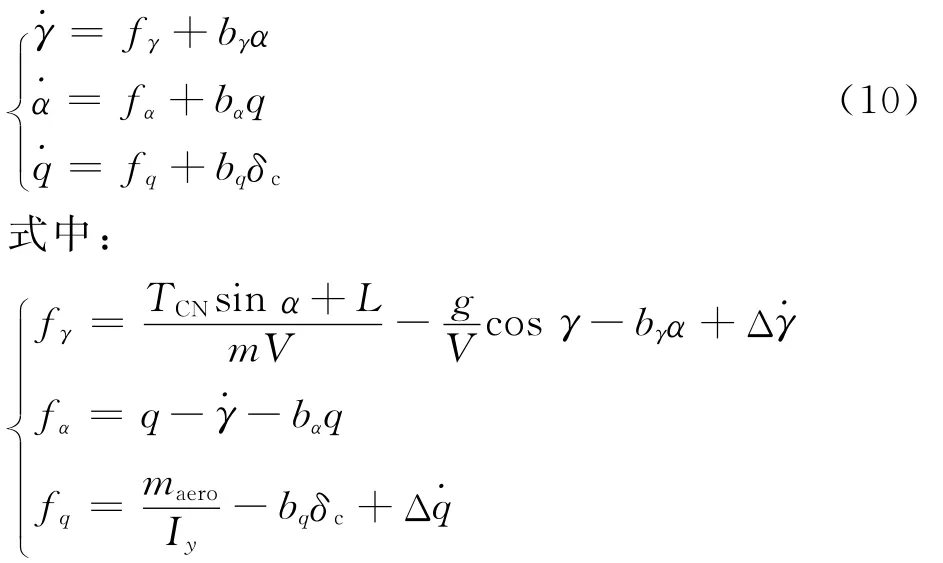
其中：Δγ、Δq为考虑由气动参数摄动、未建模动态和外界干扰等组成的复合干扰；fγ、fα、fq为包含系统内部动态的总扰动。

同时，由于物理结构的限制，V／STOL飞机执行机构的输出必然是受限的，在控制器设计时必须考虑输入受限问题对系统稳定性的影响。其中，鸭翼偏转角受限的数学模型可描述为

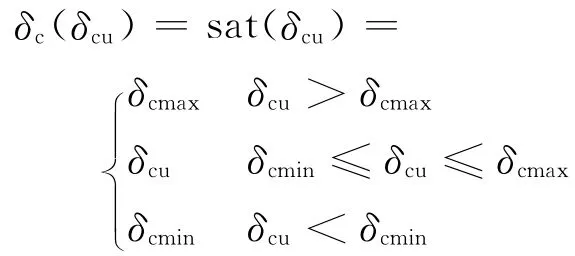
式中：δcmin＜0和δcmax＞0分别为鸭翼下偏和上偏的极限，且有 δcmin≠ δcmax；δcu为待设计的控制量。

针对爬升角仿射不确定系统（10），将ADRC突出的抗扰能力与Backstepping严格的递推分析相结合，提出一种LADRC-Backstepping控制方法，其中LADRC包含线性跟踪微分器（Linear Tracking Differentiator，LTD）、线性扩张状态观测器（Linear Extended State Observer，LESO）和线性状态误差反馈（Linear State Error Feedback，LSEF）3部分，具体形式参见文献［20］。

步骤1 考虑第1阶子系统，首先利用LTD式（11）跟踪指令信号γc并获取其微分γc，即v11→γc，v12→γc：

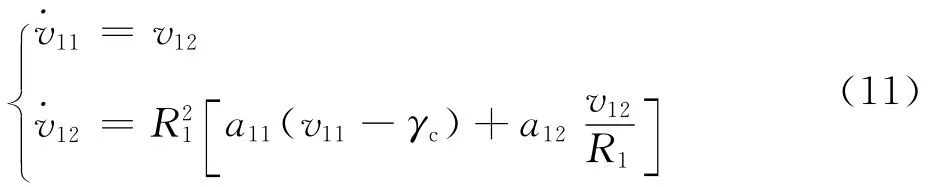
式中：R1为决定跟踪快慢的调节增益；系数a11、

定义虚拟爬升角跟踪误差eγ＝γ－v11，求导可得

对式（12）应用LESO估计fγ：

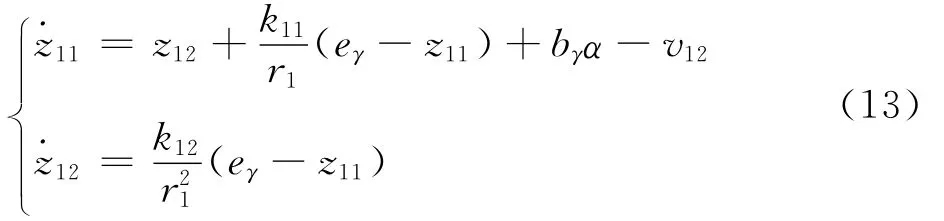
式中：r1为LESO调节增益的倒数；系数k11、k12

在z12→fγ基础上，基于LSEF设计虚拟控制律：

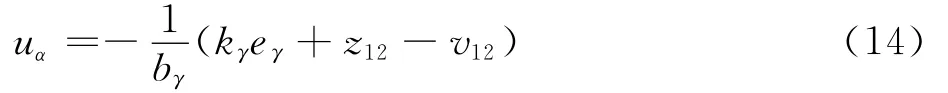
式中：kγ＞0为待设计参数。同时，再次利用LTD跟踪uα并获取uα，有v21→uα，v22→uα。

取Lyapunov函数为

定义：eα＝α－v21，ζα＝v21－uα，ξγ＝fγ－z12，则有α＝uα＋ζα＋eα，结合式（12）、式（14），对式（15）求导可得

式中：γ＝。进一步地，当eα＝0时，将为系统的干扰输入，令K＝k－，则式（16）可写为

式（17）表明：只要γ有界，eγ就有界，即系统（12）是输入到状态稳定的。

步骤2 考虑第2阶子系统，同样利用LTD跟踪第1阶子系统的虚拟控制量uα并获取其微分uα：

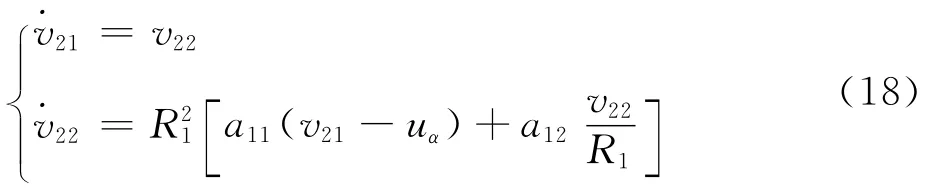
对虚拟迎角跟踪误差eα＝α－v21求导，可得

对式（19）应用LESO估计fα：

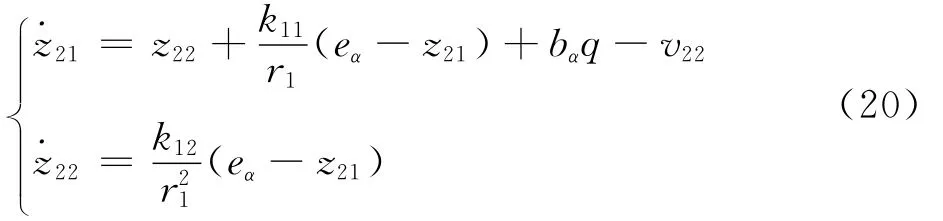
在z22→fα基础上，设计虚拟控制律：

式中：kα＞0为待设计参数。同时，再次利用LTD跟踪uq并获取uq，有v31→uq，v32→uq。

取Lyapunov函数为

定义：eq＝q－v31，ζq＝v31－uq，ξα＝fα－z22，结合式（19）、式（21），对式（22）求导可得

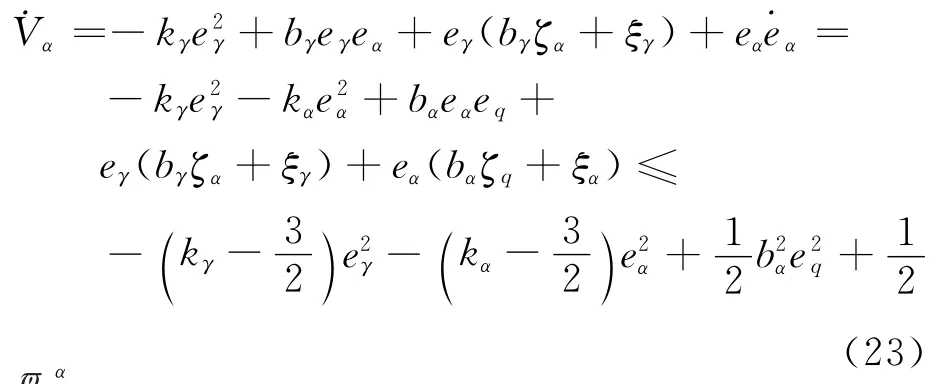
式中：α＝γ＋。进一步地，当eq＝0时，将α视为干扰输入，令eα＝ ［eγ，eα］T，Kα＝

式（24）表明：只要α有界，eα就有界，即系统（19）是输入到状态稳定的。

步骤3 考虑第3阶子系统，同样利用

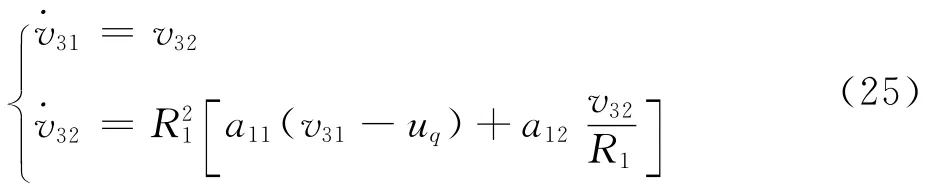
跟踪第2阶子系统的虚拟控制量uq及其微分uq，对虚拟俯仰角速度的跟踪误差eq＝q－v31求导，可得

对式（26）应用LESO估计fq：

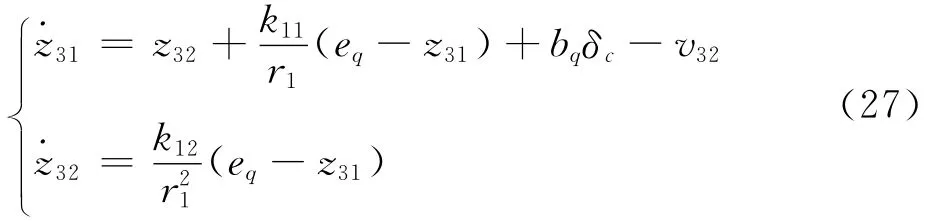
由于输入饱和的限制，会导致设计控制量δcu与实际控制量δc之间存在偏差。为此，引入如下辅助系统对偏差进行补偿：

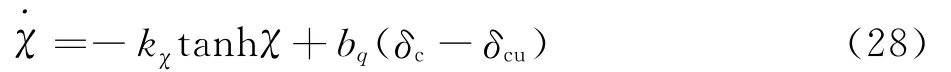
式中：χ为抗饱和补偿参数；tanh（·）∈ （－1，1）为双曲正切函数；kχ＞0为待设计参数。

定义修正的跟踪误差珓eq＝eq－χ，求导可得

针对式（29），设计鸭翼偏转控制量δcu为

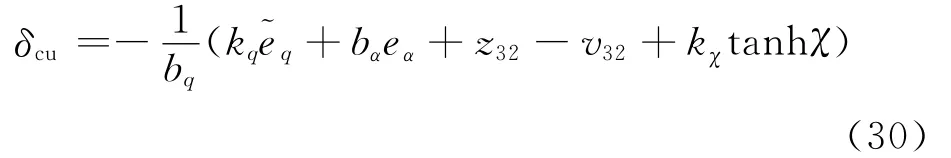
式中：kq＞0为待设计参数。

取Lyapunov函数为

定义：ξq＝fq－z32，结合式（29）、式（30），对式（31）求导可得

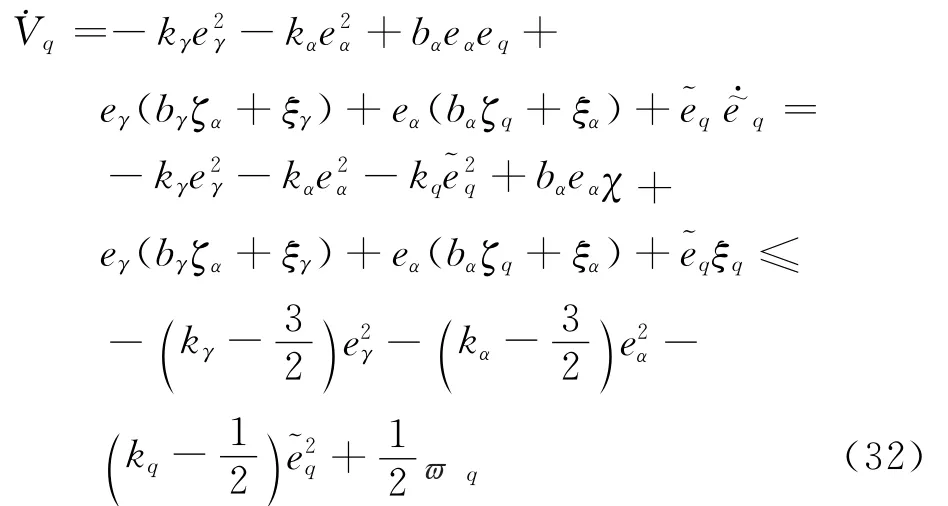
式中：q＝。将q视为干扰输入，令

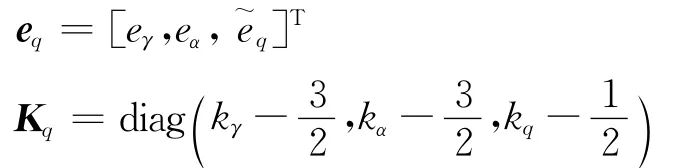
则式（32）可写为

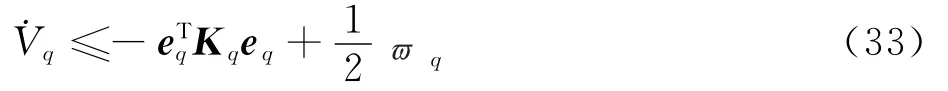
式（33）表明：只要q有界，eq就有界，即系统（29）是输入到状态稳定的。

根据上述设计过程可得定理1。

定理1 对于受非对称输入约束的爬升角子系统（10），设计虚拟控制律（14）以及（21）和真实控制律（28）和（30），则存在常数kx（x ＝γ，α，q）和kχ，使闭环系统的所有信号有界，且实际爬升角跟踪误差珓eγ＝γ－γc渐进收敛到原点的某个紧集内，该紧集的界可随kx和R1的增大而达到任意小。

为证明定理1，首先给出关于LTD式（11）／式（18）／式（25）和 LESO 式（13）／式（20）／式（27）的收敛性结论。

引理1［23］对于如下一般形式的LTD：

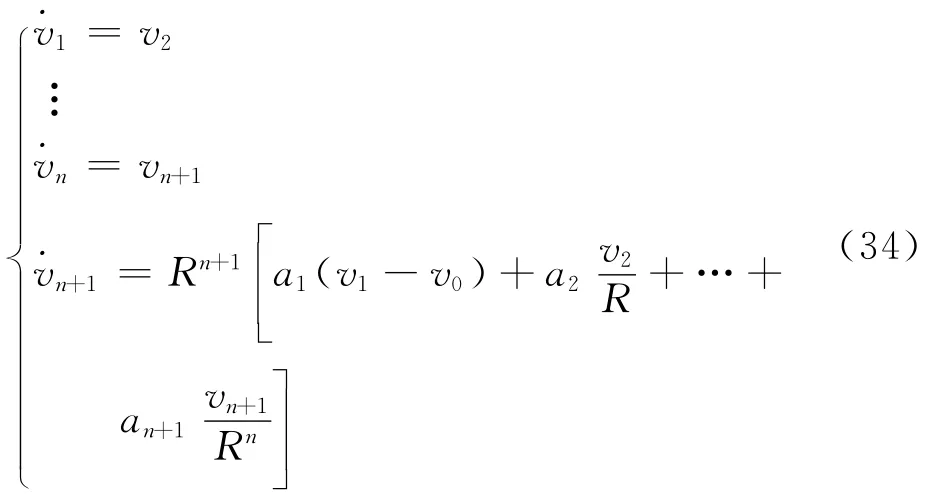
witz的，且光滑函数v0：［0，∞）→ R 满足supt∈［0，T1］v0（i）＝B＜ ∞，i＝1，2，…，n，其中常数T1，B＞0，则对任意给定的LTD式（34）的初始值以及任意的0＜τ1＜T1，当R→∞时，vj在t∈［τ1，T1］上一致收敛于v0（j－1），j＝1，2，…，n＋1。

引理2［24］对于如下一般形式的LESO：

Hurwitz的，且n阶被观测不确定系统：

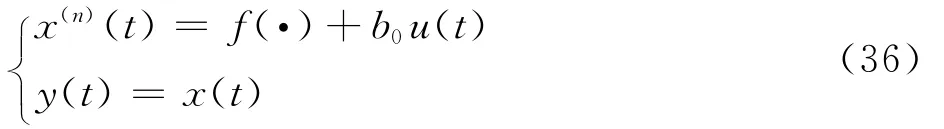
的总扰动（包含内部动态和外界干扰）的导数f有界，则对于任意给定的LESO式（35）的初始值以及任意的τ2＞0，当r→0时，zi和zn＋1在t∈［τ2，∞］上分别一致收敛于x（i－1），i＝1，2，…，n和f。

注1 对于实际飞机系统，由于飞行状态和控制输入总是有界的，外界干扰亦是有限的，因此，系统总扰动f及其导数f也是有界的。

证明：1）取辅助系统的Lyapunov函数为

令 δc－δcu≤δ珘cm，其中δ珘cm为正常数，结合式（28）和χtanhχ≥0，对式（37）求导可得Vχ＝－kχχtanhχ＋bqχ（δc－δcu）≤

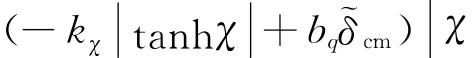
令kχ≥kχtanhχ ≥bqδ珘cm，则有Vχ≤0，从而χ有界。在此基础上，由引理1和引理2可知，对于给定的R1和r1，ζx和ξx（x＝γ，α，q）有界，从而可得x有界。

2）取闭环系统的lyapunov函数为

若eγ、eα、珓eq分别处于紧集Ωγ、Ωα、Ωq外，则V＜0，因此eγ、eα、珓eq有界。

进一步地，若令

则有V≤－μV＋ ，从而可得

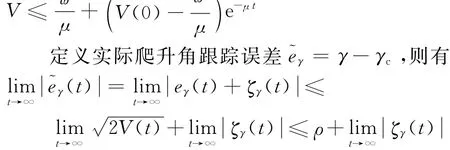
式中：ρ＝ 2 ／μ，ζγ＝v11－γc。由式（39）可知，ρ随kx的增大而减小，且有limρ＝0；由引理1可知，ζγ随R1的增大而减小，且有e珓γ的收敛半径任意小。

3）由e珓q＝eq－χ以及χ和e珓q有界可知，eq也是有界的。

3.2 俯仰角控制器设计

俯仰角控制由θ－q子系统决定，该系统可化为如下简单的二阶仿射形式：

针对系统（40），直接基于 LADRC［20］设计的俯仰角控制器如下：

定理2 针对俯仰角子系统（40），设计线性自抗扰控制律（41），则俯仰角跟踪误差珓eθ＝θ－θc最终有界。

为证明定理2，首先给出关于LADRC式（41）的一般形式的收敛性结论。

引理3［20］对于不确定系统（36），若f有界，设计由 LTD 式 （34）、LESO 式 （35）和 如 下LSEF：

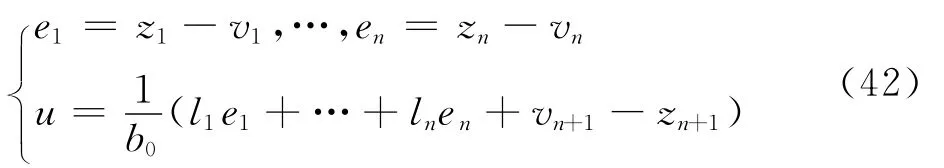
证明：定义ζθ＝v41－θc，由引理1可知，ζθ有界；定义eθ＝θ－v41，由于fq总是有界的，根据引理3，eθ最终有界；因此可得珓eθ＝eθ＋ζθ亦最终有界。

4 短距起飞全过程仿真

基于上述优化操控策略，本节进行短距起飞全过程仿真，式（4）、式（8）中的气动系数参考文献［25］，本文对其数据进行插值拟合处理。其中，在舰面滑跑段，预设δCN1＝45°，δLF1＝30°，飞机初始状态见2.1节；离舰初期，预设δCN2＝0°，δLF2＝60°；进入爬升角控制段，设定指令信号γc＝10°，发动机最大加力推力TCN＝191.3kN，根据此阶段的初始飞行状态取bγ＝1，bα＝1，bq＝5，在不考虑干扰因素的情况下，调节LADRC-Backstepping控制器参数为R1＝10，a11＝－1，a12＝－2，r1＝0.001，k11＝2，k12＝1，kγ＝1.8，kα＝6，kq＝7.2，kχ＝11；当h＝300m时转入俯仰角控制段，此时令δf＝0°，减小发动机推力至TCN＝124.6kN，设定指令信号θc＝10°，调节LADRC控制器参数为R2＝10，a21＝－1，a22＝－3，a23＝－3，r2＝0.1，k21＝3，k22＝3，k23＝3，l1＝－1，l2＝－2。

为验证系统的鲁棒性，在不改变上述控制器参数的情况下，加入不确定项 Δγ 和 Δq，其中 Δγ为频率1rad／s、幅值0.02的正弦波信号，Δq为功率0.1的白噪声与频率1rad／s、幅值0.02的正弦波的组合信号；同时在20～25s和35～45s时分别加入水平和垂直突风，突风模型采用典型的半波长（1-consine）离散模型：

式中：dm为突风尺度，VWm为突风强度，分别代表突风最大时的位置和速度；x为进入风场后的飞行距离，设定xg、h方向的dm分别为1 500m、500m，对应的VWm分别为－10m／s、12m／s。

同时，为显示本文所提策略的优越性，加入“一次预设推力偏转角＋俯仰角控制”的传统操控策略进行比较。取仿真步长d＝0.001，仿真结果如图3所示。从图中可以看出：

1）在多矢量推力的作用下，V／STOL飞机在甲板上滑跑149.7m（5.9s）后离舰（表1）；之后经推力矢量的二次优化配置，推力向后偏转使加速度增大，同时受其本身动力学特性的影响，俯仰角有呈衰减振荡变化的趋势；但仅一个波峰后（7.5s）飞行速度即达到75m／s，推力矢量关闭，飞机进入爬升控制状态，飞行姿态的振荡趋势被拟制并逐渐趋于稳定。但在传统操控策略下，Txb不变而飞行阻力和爬升角逐渐增大，导致空速增加缓慢，又由于mprop仍然较大，因而俯仰角经历了一个较长时间的震荡增长过程。

图3 短距起飞全过程的飞行状态变化曲线Fig.3 Variations of flight state during the whole short take-off process

2）当V／STOL飞机处于爬升角控制时，爬升角能够迅速无超调地跟踪指令信号并保持，爬升速度wg明显加快，经14.1s飞机高度从43.5m升至300m；水平逆风的加入使空速增加，又使wg有所增大，但爬升角的控制性能几乎不受各类干扰因素的影响；同时在此阶段，辅助补偿机制的引入有效减小了控制量，避免了鸭翼偏转角进入饱和状态（δcmin＝－45°，δcmax＝30°）。而传统策略下虽然飞行速度增加缓慢，但较大的Tzb使爬升角不断增大，从而使飞机具备一定的爬升率，并经27.5s升至300m高度。

3）当V／STOL飞机转入俯仰角控制时，在相同的LADRC控制器的驱动下，鸭翼迅速下偏（前缘下偏后缘上偏）产生低头力矩以减小俯仰角，虽然惯性使俯仰角的修正有所过度，但鸭翼能够很快调整并最终使俯仰角稳定在给定值，且整个过程由于LESO对各类干扰因素的实时估计和补偿，使鸭翼和俯仰角的响应免受影响。

综上所述，本文所提出的分段优化操控策略对V／STOL飞机的短距起飞模式具有较好的控制性能，对内部不确定性和外界干扰亦具有较强的鲁棒性，同传统操控策略相比，在稳定飞行姿态和提高爬升速度等方面具有明显的优越性。

5 结 论

本文针对V／STOL飞机在有限的甲板上实施滑跑起飞以及快速、稳定爬升的实际需要，提出了一种“二次预设推力偏转角＋爬升角控制＋俯仰角控制”的优化操控策略，仿真结果验证了该策略的有效性和优越性。

1）建立了V／STOL飞机在短距起飞模式下的全过程动力学模型，体现了推力矢量控制的运动特性。

2）提出了两次预设推力偏转角来提升短距起飞性能的推力矢量控制策略，给出了舰面滑跑段和离舰初期的预置推力偏转方案，分别实现了舰面滑跑距离最短和离舰后增速时间最短。

3）针对非对称输入约束下的纯反馈非仿射型的爬升角系统，提出了一种LADRC-Backstepping控制方法，其中引入一种辅助补偿机制避免了控制量长时间陷入饱和，最终实现了复合干扰和短时突风影响下的爬升角指令的稳定跟踪，有效提升了V／STOL飞机的爬升速度。

4）直接基于LADRC设计了俯仰角控制器，实现了对系统内部动态、复合干扰和由短时突风引起的状态变化的综合精确估计，从而确保了对俯仰角指令的精确跟踪，使V／STOL飞机最终以稳定的姿态爬升。