旋翼地面效应的气动建模与特性
谭剑锋*,周天熠王畅,于领军
1.南京工业大学 机械与动力工程学院,南京 2118162.清华大学 航天航空学院,北京 1000843.中国空气动力研究与发展中心 旋翼空气动力学重点实验室,绵阳 6210004.陆军航空兵学院 航空机械工程系,北京 101123
相比于无地效状态,地面效应能提高旋翼气动性能,但产生包括下洗和地面射流等复杂流场,从而导致旋翼操纵困难[1-2],尤其是超过一定速度的地面射流将扬起沙尘,从而产生“沙盲(Brownout)”现象[3-4],并阻碍飞行员视线而导致飞行事故。此外,对旋翼地面效应下复杂流场特性的研究是解决“沙盲”现象的前提[1]。因此,研究旋翼地面效应下旋翼尾迹变化特性和复杂流场就显得非常重要。
针对地面效应对旋翼气动特性的研究,早期建立多种地面气动模型。通过采用源或汇模拟旋翼,并采用镜像源或汇体现地面边界条件,建立了模拟地面效应的镜面方法[5-6],但此方法并未考虑到旋翼尾迹的影响。为此,Rossow[7]通过增加圆柱涡面考虑旋翼尾迹效应。此外,基于叠加原理耦合旋翼涡流理论和映象法,何承健和高正[8]通过涡圈考虑旋翼尾流效应和卷起,然而方法中并未考虑旋翼桨叶片数和尾流收缩效应。基于此,DuWaldt[9]通过采用连续畸变螺旋涡线模型考虑桨叶桨尖涡和尾流收缩效应的影响,并通过镜像尾迹模型体现地面效应,但此方法并未考虑旋翼桨尖涡与地面的非定常干扰。随后,Ferguson[10]与Preston等[11]基于动量理论,耦合射流理论,并基于试验数据估算地面效应修正因子,兼顾旋翼尾流收缩效应,建立了旋翼地面效应气动分析简化模型,用于分析地面效应下旋翼性能,然而此方法需要大量的试验数据来获得模型中的修正因子,难应用于各种旋翼构型。鉴于此,通过旋翼自由尾迹模型模拟旋翼桨尖涡的变化特性,并采用镜像尾迹模拟地面的无穿透条件,从而建立基于自由尾迹和镜面尾迹的旋翼地效气动分析方法[12-14]。与此类似,通过采用涡量输运模型(Vorticity Transport Model,VTM)[15]或黏性涡粒子法[16]模拟旋翼尾迹和地面镜像尾迹,从而分析旋翼桨尖涡在地面效应下的变化特性和“沙盲”现象[15]以及缩比旋翼地效下的流场特性,但此类镜像方法难适用于复杂地面。为此,基于汇的地面面元气动模型,耦合旋翼自由尾迹模型,建立旋翼地面气动效应分析方法[17-18],然而此方法仍未考虑地面的无滑移边界条件和黏性效应。
近年来,基于Euler体系的计算流体力学(Computational Fluid Dynamics,CFD)已逐步应用于旋翼复杂流场分析[3,19-21]。由于 CFD 存在较大的数值耗散,需要数量庞大的精细网格,因此在准确捕捉旋翼桨尖涡方面仍需进一步发展,且CFD计算量较大,尤其在需要准确捕捉旋翼桨尖涡结构的旋翼地面效应分析方面[19]。
基于Lagrangian体系的黏性涡粒子方法能准确捕捉旋翼桨尖涡结构,且能较好计算旋翼/机身/尾桨气动干扰下的非定常气动载荷[22-24]。为此,本文将采用非定常面元/黏性涡粒子法模拟旋翼桨叶非定常气动载荷和旋翼尾迹非定常时变效应,并基于涡面和无滑移边界条件,求解第2类Fredholm方程获得地面涡面矢量分布,将涡面矢量按照涡扩散方程扩散到流体中,建立考虑黏性效应的地面气动模型,且与非定常面元/黏性涡粒子法耦合,构建旋翼地面效应气动分析方法。通过计算Lynx尾桨地面效应下尾桨性能、桨尖涡轨迹,并与NASA试验和CFD结果对比验证本文方法捕捉地面效应下旋翼尾迹的准确性。此外,计算Maryland大学缩比旋翼和NASA缩比旋翼地面效应状态下的复杂流场,并与试验结果和CFD结果对比,验证本文方法计算旋翼地面效应下复杂速度场的准确性。
1 计算方法
1.1 旋翼气动模型
旋翼地效的复杂流场主要受旋翼尾迹影响,而旋翼尾迹受到旋翼气动模型影响显著。为此,为计算旋翼桨叶非定常气动载荷特性和旋翼尾迹涡量分布,采用非定常面元法模拟旋翼桨叶气动特性[22]。基于地面坐标系(图1),流场势函数φ可表示为
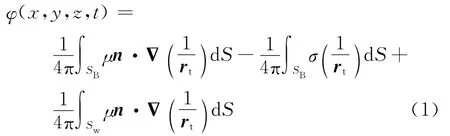
式中:σ、μ、SB、Sw、n、rt分别为汇、偶极子、桨叶表面、尾迹涡面、桨叶表面法矢量、空间位置矢量。
根据旋翼桨叶边界条件和非定常面元法,旋翼气动模型边界条件为

式中:vB为桨叶速度。
基于Neumann边界条件和后缘Kutta条件将上述条件转化为代数方程,并求得旋翼桨叶σ和μ分布。随后基于非定常伯努利方程,确定旋翼桨叶压力分布:
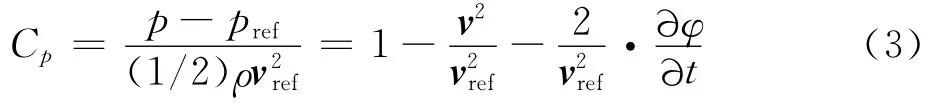
式中:pref、ρ、v、p、vref分别为参考压力、空气密度、当地速度矢量、压力、参考速度矢量。
计算得到桨叶非定常气动载荷为
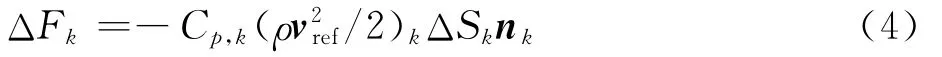
式中:ΔFk、ΔSk、nk分别为桨叶面元的气动力、面积、法向矢量。

图1 旋翼地面效应气动模型示意图Fig.1 Schematic of a rotor aerodynamic model in ground effect
1.2 旋翼尾迹模型
旋翼尾迹将主导地面效应下的复杂速度场,且为准确模拟旋翼地面效应下的速度变化特性,需准确捕捉靠近地面的旋翼尾迹结构,因此,本文将采用基于三维不可压黏性Navier-Stokes方程的黏性涡粒子法[22-24]计算旋翼涡量场分布:
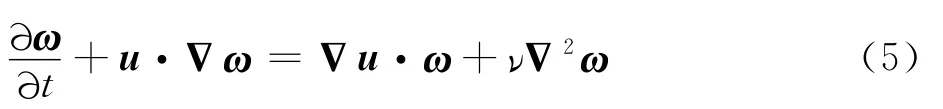
式中:ν、ω、u分别为运动黏性系数、涡量、速度矢量。
采用 4th-Runge-Kutta格式、Biot-Savart定律[22]求解式(5)的涡量输运效应。采用粒子强度交换(Particle Strength Exchange,PSE)法求解式(5)右端的黏性耗散项νΔ2ω:
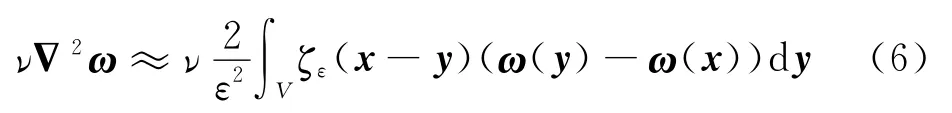
式中:ζε为高斯函数;ε为涡核半径;V为体积。
采用直接求解法将涡粒子速度梯度表示成核函数梯度和位置梯度的积,从而求解式(5)右端的拉伸项Δu·ω:

式中:K为Biot-Savart核函数;αj为第j个涡粒子涡矢量。
此外,采用多极子展开法(Fast Multipole Method,FMM)[25]对旋翼流场加速求解,且基于Neumann将旋翼后缘脱体尾迹面元转化为涡粒子,并按照式(5)控制方程计算旋翼涡量场分布。
1.3 地面气动模型
地面将改变旋翼尾迹和流场特性,为此,基于涡面矢量和无滑移边界条件建立适合于旋翼地效的地面气动模型。根据 Poincaré规则[26-28],采用第2类Fredholm方程建立地面无滑移边界条件等效方程:

式中:uslip为旋翼桨叶和尾迹诱导的滑移速度;γ为满足无滑移边界条件的地面涡面涡矢量;t为地面切矢量;KG为自由空间的Green函数梯度,即 K(x,x′)= ΔG(x,x′)。
式(8)确定了地面涡面分布。根据流函数与涡量场之间的关系,对于无旋的物体,上述无滑移边界条件可确保物体表面满足无穿透边界条件[27]。将地面离散为四边形单元,每个单元均需满足式(8)的边界条件。假设每个单元的涡面涡矢量均匀分布,因此式(8)可以转化为一系列的代数方程:
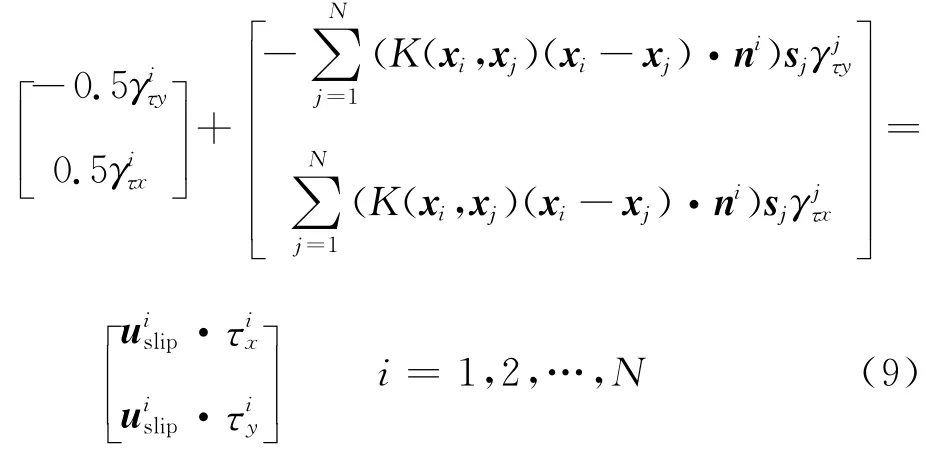
黏性流体中,地面对流体的作用力将流体速度降低至0,即地面是流体涡量的源头,涡量从地面进入流体可通过涡通量描述[29-31]。在求得地面涡矢量分布后,通过求解涡扩散方程将地面涡矢量扩散到流体中,即
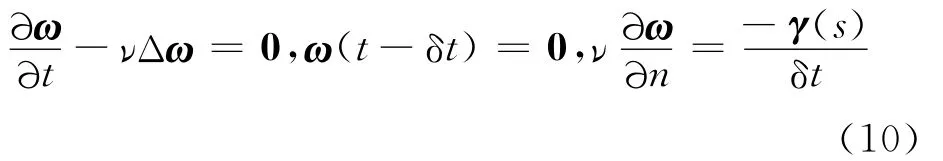
将式(10)表述成积分形式[26]:
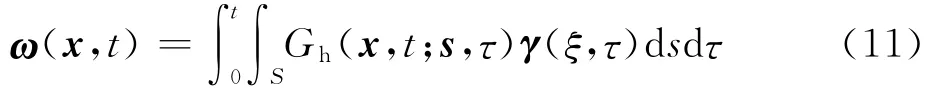
式中:Gh为三维热扩散核函数;S为涡面。
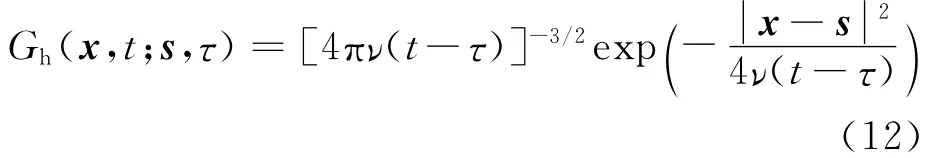
为求解涡量扩散方程,采用离散非均匀Neumann问题的Green积分函数,从而获得地面涡量γ扩散到流体的涡量,即

将扩散得到的涡量进行积分,获得等效涡粒子(如图2所示),即

式中:(xi,yi,zi)和(hxi,hyi,hzi)分别为涡粒子位置矢量和流体积分体的长度尺寸。
由此获得地面涡矢量扩散到流体中的涡粒子涡矢量导数为
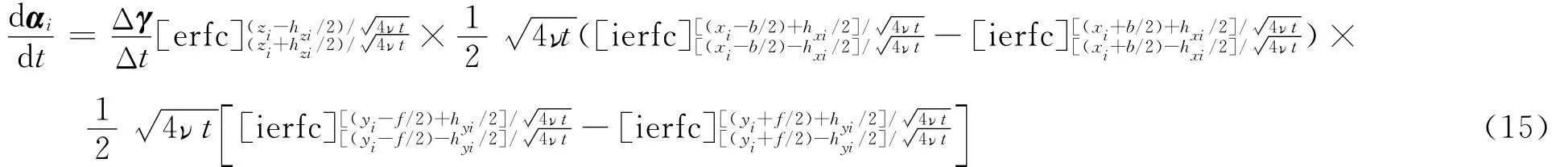
通过对式(15)进行积分获得涡粒子涡矢量。

图2 涡面涡矢量扩散到涡粒子Fig.2 Diffusion of ground vortex sheet to vortex particles
2 旋翼地面效应气动特性
2.1 桨尖涡轨迹
本算例计算Lynx全尺寸尾桨地面效应下的桨尖涡轨迹[32]。尾桨由4片无扭转矩形桨叶组成,桨叶半径R、弦长、翼型、桨尖马赫数Ma、实度分别为1.105m、0.18m、NPL9615、0.56、0.208。尾桨计算模型由弦向为60段、展向为20段的桨叶组成,地面离散为1 600个涡面单元的8m×8m矩形面,如图3所示,h为旋翼距离地面高度。
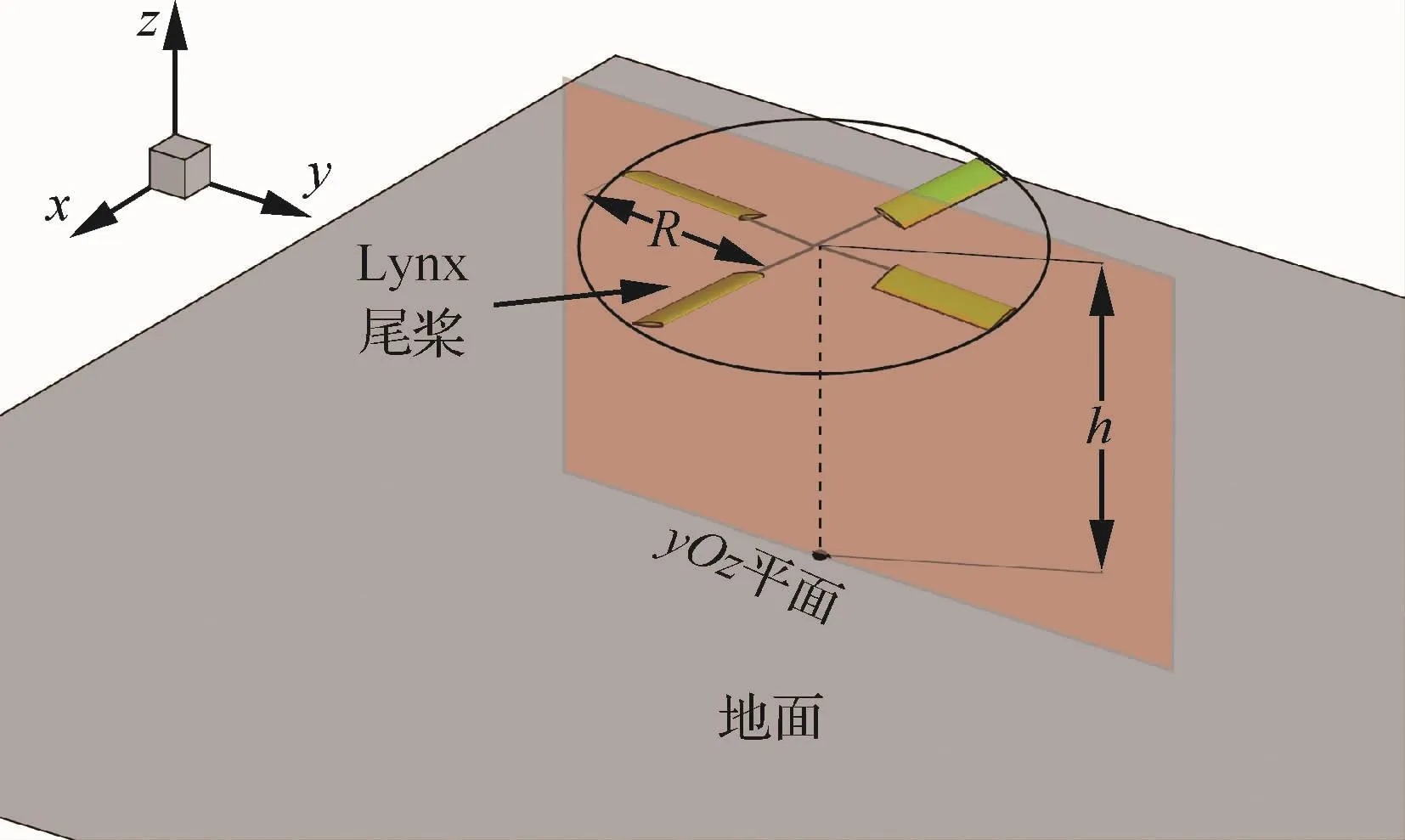
图3 Lynx尾桨地面效应模型Fig.3 Model of Lynx tail rotor in ground effect

表1 不同地面高度下的尾桨拉力和功率与试验对比Table 1 Comparison of thrust and power with experiment at different tail rotor heights
保持尾桨总距不变,计算得到不同高度状态下的尾桨拉力系数CT和功率系数CP,如表1所示,其中CT,OGE为无地效尾桨拉力系数,CP,OGE为无地效尾桨功率系数。计算得到不同高度下的尾桨拉力系数和功率系数与NASA AMES试验测量结果[32]基本一致。此外,降低尾桨离地面高度,尾桨拉力系数增加,而功率系数则略有减小,此现象与NASA试验测量结果非常吻合。
采用本文方法计算得到无地效状态下Lynx尾桨截面涡量分布和桨尖涡轨迹分别如图4(a)和图4(b)所示。随着桨尖涡涡龄角的增加,桨尖涡明显收缩,然而,当涡龄角大于270°时,桨尖涡逐步扩散。此外,随着桨尖涡向下游移动,桨尖涡逐步呈现出非定常特性,且沿着径向扩大。
图4(b)中同时给出了涡输运模型(VTM)[4]、CFD[33]以及 NASA 试验测量结果[32]。VTM 采用时间推进格式求解涡量形式的Navier-Stokes方程,采用升力线模型模拟旋翼气动力,并通过镜像技术模拟无黏地面。CFD则采用FLOWer软件,通过求解雷诺平均Navier-Stokes方程,湍流模型采用k-ω模型,且通过嵌套网格技术实现旋翼流场模拟(文献[33]未给出计算模型网格)。CFD计算得到的桨尖涡径向收缩过大,且涡龄角大于180°的桨尖涡轴向移动速度过大。相反,VTM计算得到的桨尖涡轴向移动速度过小。本文方法计算得到的桨尖涡径向收缩和轴向移动速度均与试验结果吻合很好。此外,涡龄角大于180°后桨尖涡的径向位置出现波动,由此表明桨尖涡存在非定常时变特性,此现象与试验结果吻合。
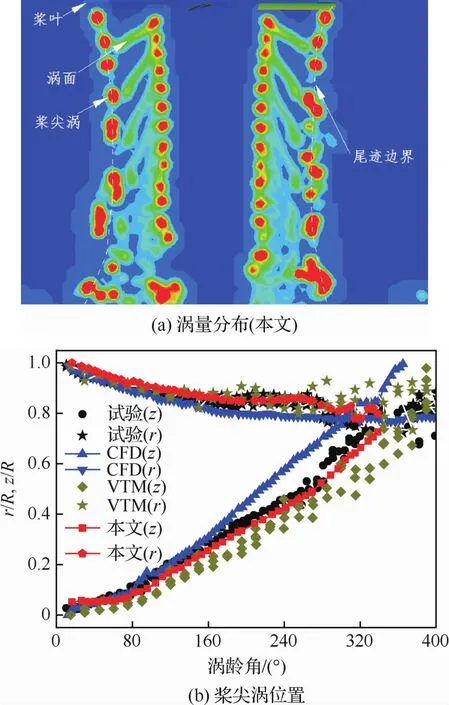
图4 无地面效应的尾桨桨尖涡轨迹Fig.4 Trajectories of tip vortex of tail rotor without ground effect
计算得到尾桨距离地面高度h/R=1.54、0.84、0.52状态下尾桨桨尖涡的轴向和径向位置如图5所示,图中同时给出了VTM和CFD计算结果以及试验结果。当h/R=1.54(图5(a)),涡龄角小于180°时,计算得到尾桨桨尖涡径向收缩,且与CFD和试验结果均吻合。随着涡龄角逐渐增加,CFD计算得到的桨尖涡径向和轴向位置均偏离试验测量结果,而本文方法计算得到的尾桨桨尖涡径向收缩、扩张、轴向移动均与试验吻合得很好。相比于h/R=1.54状态,h/R=0.84(图5(b))状态下的桨尖涡径向收缩和扩张更明显,轴向移动更慢,表明地面对尾桨桨尖涡运动轨迹影响更大,主要原因在于地面阻塞作用更强,由此导致桨尖涡扩张速度更大,轴向速度更小。此外,VTM计算的轴向位置低于试验测量结果,CFD计算的轴向位置则略大,而本文方法计算的桨尖涡径向和轴向位置均与试验结果比较吻合。当h/R=0.52时(图5(c)),CFD较好捕捉桨尖涡径向收缩,但涡龄角大于240°时,桨尖涡扩张明显大于试验测量结果。VTM方法能较好模拟桨尖涡的收缩和扩张,然而桨尖涡轴向位置明显低于试验测量值,尤其是涡龄角大于240°时。本文方法计算的桨尖涡径向收缩、扩张和轴向位置均与试验测量结果吻合较好,表明本文计算方法能较好捕捉地面效应下的桨尖涡收缩、扩张等特性。

图5 地面效应下尾桨桨尖涡径向和轴向位置Fig.5 Tip vortex axial and radial locations oftail rotor in ground effect
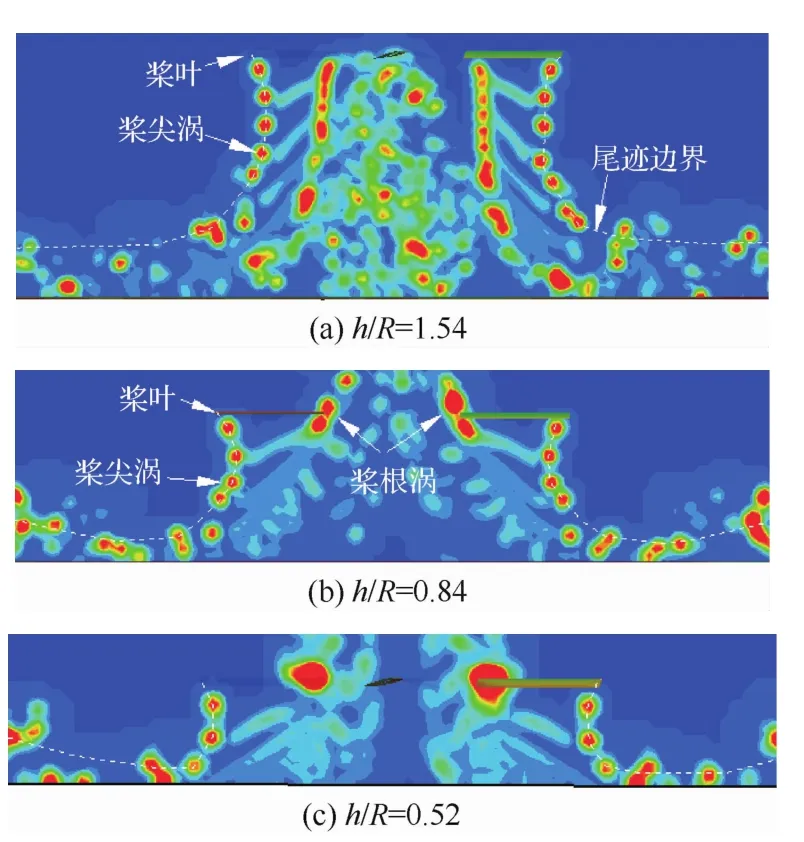
图6 地面效应下尾桨涡量分布Fig.6 Vorticity distribution of tail rotor in ground effect
计算得到尾桨距离地面高度h/R=1.54、0.84、0.52状态下尾桨涡量分布如图6所示。相比于无地效状态,地面效应下的桨尖涡径向和轴向位置均产生明显变化。当h/R=1.54时,桨尖涡在第1圈至第2圈均收缩,随后逐渐扩张。此外,降低尾桨距离地面高度至h/R=0.84,桨尖涡在涡龄角小于180°均收缩,随后开始扩张。相比于h/R=1.54,此时桨尖涡扩张对应的涡龄角显著提前。当尾桨距离地面高度降低至h/R=0.52,桨尖涡收缩和扩张转换对应的涡龄角提前至90°,且扩张速度明显增加。因此,降低尾桨距离地面高度,桨尖涡扩张更早,且扩张速度更大。
相比于无地效状态,地面效应下的桨尖涡轴向位置减小,且随着尾桨距离地面高度的减低而逐渐减小。此外,h/R=0.84和0.52状态下桨根涡向上移动,且随着尾桨距离地面高度的降低而更加明显。
2.2 地面射流
本算例计算地面效应下旋翼径向速度随高度的变化特性。算例采用Maryland大学模型旋翼[33],旋翼由两片无扭转的矩形桨叶组成。桨叶的半径、弦长、展弦比、实度、桨尖Ma、翼型分别为86mm、19.6mm、4.39、0.14、0.08、圆弧翼型。旋翼桨尖平面平行于地面,总距和距离地面的高度为12°、1.5R。旋翼计算模型由弦向为60段、展向为20段的桨叶组成,地面离散由1 600个涡面单元的0.8m×0.8m矩形组成。
计算得到的旋翼桨尖涡结构如图7所示,同时,图中给出了Maryland大学试验测量结果[34]。图7中清晰显示了旋翼尾迹中的外侧桨尖涡与内侧涡面以及靠近地面的射流,且计算得到的尾迹结构与试验测量结果较好地吻合。此外,桨尖涡从桨叶后缘脱离后径向收缩,而后在靠近地面时扩张。桨尖涡在螺旋运动4圈后相互诱导,逐步耗散。在桨尖涡靠近地面时,出现局部“涡对”现象,主要原因为随着桨尖涡靠近地面,桨尖涡之间的轴向距离减小,相互诱导效应增强。在地面黏性的作用下,耗散效应增强,且桨尖涡逐步拉伸扩张,形成靠近地面的地面射流。
计算得到桨叶内侧涡面结构与试验测量结果(图7(a))基本吻合,且涡面结构在2圈之内清晰展现。相比于旋翼桨尖涡,内侧涡面向下移动速度更大,逐步与桨尖涡相互干扰,并最终融合于桨尖涡。
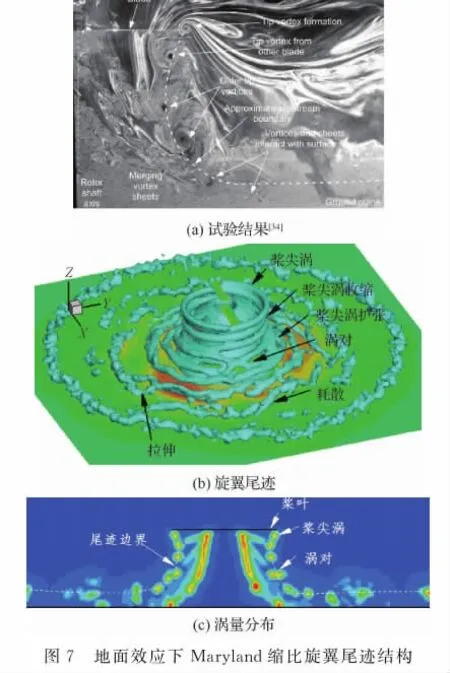
Fig.7 Wake structure of the Maryland scaled-rotor in ground effect
计算得到6个径向位置(r/R=0.8,1.0,1.25,1.50,1.75,2.00)处的径向速度随高度变化如图8所示,图中给出了试验测量结果[34]和CFD结果[19]。CFD计算采用基于雷诺平均Navier-Stokes方程的OVERTUNS软件,包括双时间步推进格式、低Ma预处理、3阶 MUSCL(Monotone Upstream centered Schemes for Conservation Laws)和5阶 WENO(Weighted Essentially Non-Oscillatory)格式、VTGs(Vortex Tracking Grids)、Roe通量差分格式以及Spalart-Allmaras湍流模型,网格数量为2.14×107。本文方法计算得到的径向速度随高度变化与试验和CFD结果均吻合较好,且本文计算的径向速度峰值所对应的离地高度与CFD计算结果吻合较好,均略大于试验测量值。在r/R=0.80,1.00,1.25,1.50处,本文计算结果与CFD结果吻合非常好,但两种方法计算的峰值均小于试验测量结果。此外,在r/R=1.50和1.75处,CFD计算的径向速度峰值大于试验测量值,而本文计算方法得到的径向速度峰值略小于试验测量值。在r/R=2.00处,CFD计算的径向速度峰值大于试验测量值,本文计算的径向速度峰值与试验测量结果较吻合。由此表明本文计算方法可较好模拟旋翼地面效应下的径向速度分布特性。

图8 地面效应下不同径向位置的径向速度Fig.8 Radial velocities at different radial locations in ground effect
随着高度降低,径向速度先增加后快速减小,形成径向地面射流现象,主要原因在于旋翼尾迹靠近地面被迫扩张,下洗流从垂直方向逐渐过渡到径向方向。由此也表明本文方法较好地捕捉径向地面射流现象。随着径向位置的增加,计算得到的地面射流厚度逐渐减小,而射流速度峰值先增加后减小,并与试验结果一致。
2.3 速度场
本算例计算地面效应下模型旋翼的速度场[34],模型旋翼由3片桨叶组成,桨叶半径、实度、桨尖速度、旋翼拉力系数、距离地面高度分别为0.16m、0.057、59.4m/s、0.006 1、1.156R,负扭采用CH-47D桨叶负扭。旋翼计算模型由弦向为60段、展向为20段的桨叶组成,地面(2.0m×2.0m)则离散为6 400个涡面单元。
计算得到3个径向位置(r/R=0.60,0.75,0.80)的垂向速度随高度变化如图9所示,图中同时给出了试验测量结果[35]。本文计算的垂向速度随高度变化与试验测量结果基本吻合。在r/R=0.60处,z<0.5D 时,D 为桨叶直径,垂向速度大于试验测量值,而在r/R=0.75和0.80处,计算的垂向速度与试验测量结果吻合得非常好。主要原因在于文中未考虑试验机身和测试平台的影响,且机身和测试平台对桨叶内侧的速度场影响略大。此外,在3个不同的径向位置,垂向速度峰值所对应的高度均相同,约为0.4D,且计算结果与试验吻合得非常好,由此表明本文计算方法能较好模拟地面效应下旋翼尾迹收缩效应和旋翼流场。
计算得到无地效和地面效应下旋翼垂向速度随径向分布如图10所示。相比于无地效状态,地面效应下的旋翼桨尖涡先收缩,而后显著扩张,由此导致垂向速度峰值所对应的径向位置增加。此外,受到地面效应影响,旋翼桨尖涡垂向间距压缩,导致旋翼垂向速度小于无地效状态。同时,受到地面的阻塞效应,桨根涡向上移动,导致桨根处垂向速度向上。

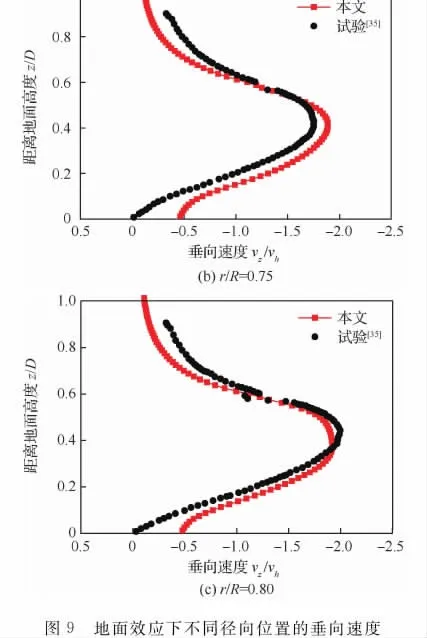
Fig.9 Vertical velocities at different radial locations in ground effect
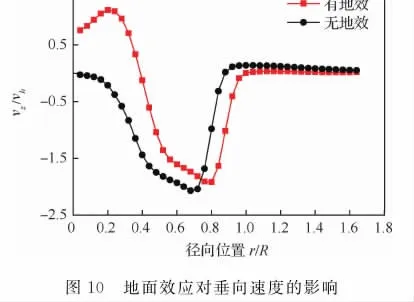
Fig.10 Influence of ground effect on vertical velocity
3 结 论
1)建立满足无滑移边界条件的地面气动模型,并耦合非定常面元/黏性涡粒子法发展旋翼地效气动分析方法,计算得到的旋翼拉力系数、功率系数、桨尖涡轨迹、垂向速度和径向速度均与试验测量结果吻合较好,表明本文计算方法的可靠性。
2)本文计算方法能较好捕捉地面效应下旋翼桨尖涡的径向收缩、径向扩张、涡对、地面射流等物理现象。
3)旋翼距离地面高度减小,桨尖涡径向扩张提前,且径向扩张速度更大,轴向移动速度更小,桨根涡向上移动更加明显。
4)地面效应下,旋翼桨尖涡轴向距离压缩,且逐步拉伸扩张,并与地面干扰形成地面射流现象。随着径向位置的增加,计算得到的地面射流厚度逐渐减小,而射流速度峰值先增加后减小。
5)相比于无地效状态,地面效应下的旋翼垂向速度峰值减小,且所对应的径向位置增加,同时桨根处垂向速度向上。

