连续钢板组合梁桥合理断面设计研究

苏 航

同济大学 土木工程学院,上海 200092

钢桥的应用与发展离不开钢材产量和材料的更新.近年随着工业技术的发展，钢材质量与产量有了大幅提高,我国钢材产量由20世纪末的6 635万t增长到了2013年的10亿t以上,达到全球产量的1/2[1]，Q 345,Q 370,Q 420等优质高强结构得到广泛应用.钢材质量已达到世界先进国家常用桥梁结构钢的要求,材料出口韩国、美国等发达国家.另一方面,随着国民收入的增加,近年劳动力成本和砂石料价格有了大幅度增加,混凝土的单价超过了600元/t,混凝土桥梁的造价相对提高.合理的钢桥结构设计,有可能使得钢桥的经济性可与混凝土桥梁相比,甚至更加经济[2-7].因此,很有必要对中小跨径公路钢桥的合理构造和标准化[8-9]展开研究,使得钢桥结构达到适用、安全、经济、美观、耐久的目的.本文拟分析钢板梁桥主梁最优设计高度,并据以给出不同跨径下的钢板梁桥截面推荐参数及其对应的造价,并给出其最优推荐方案.

1 钢板梁桥主梁最优高度的导出

主梁设计时,通常应力控制法的用钢量比刚度控制法的用钢量少,因此,本文采用截面应力控制法设计如图1所示[10]的钢板主梁.图1中σta为最大容许拉应力,MPa;σca为最大容许压应力，MPa；h为腹板高度，m；H为梁高，m；t为腹板厚度，m；Ac为受压翼缘面积，m2；At为受拉翼缘面积，m2；yc为截面形心轴至上翼缘的距离，m；yt为截面形心轴至下翼缘距离，m;M为作用弯矩,kN·m.

图1 钢板梁截面Fig.1 Steel plate beam section

因与工字钢整体的惯性矩相比，工字钢上、下翼缘相对本身形心轴的惯性矩极小可忽略不计.在此简化设计条件下,钢板梁桥腹板最优高度导出如下:

(1)

由截面内力与外力平衡关系可得:

(2)

联立式(1)与式(3)求得翼缘板所需面积:

(3)

将式(3)代入主梁截面面积公式A=Ac+At+ht，可得:

(4)

在式(4)中的M,σca,σta,t值为常数、h为变量的条件下，主梁截面面积A达到最小值(即极小值)时，由dA/dh=0可得此时的腹板高度:

(5)

《我国公路简支钢混组合梁合理截面研究》[11]对活载组合梁合理梁高做了探讨.该文采用Q 345 钢材,假设弯拉最大设计应力σta=[σ]=210 MPa;考虑到翼缘受压时局部稳定问题,假设弯压最大设计应力σca=0.9[σ]=189 MPa .本文式(5)中的最大允许拉应力σta、最大允许压应力σca分别按钢材强度设计值的80 %即220 MPa计取.

计算截面最大作用弯矩M时考虑恒载、温度荷载、车辆荷载、收缩徐变等荷载.活载标准按公路I级车道荷载计算.荷载横向分配不均匀系数假设为1.15.计算恒载时,假设沥青混凝土铺装层厚7 cm,桥面板厚度tc=k1(3b+11),式中b为主梁间距，m；k1为与荷载大小有关的系数,按1.2计取.钢梁单位桥面面积自重ω=[2.0+0.05(L-30)],式中ω为单位桥面面积自重，kN/m2；L为主梁计算跨径，m.活载冲击系数μ=15/(37.5+L).混凝土的徐变与收缩按有效弹性模量法计算,收缩按降温15℃计算.依据上述荷载标准建立Midas简支梁模型，可得到不同跨径、桥宽及主梁间距下的跨中最大作用弯矩M及支点处最大剪力Q.取常用腹板厚度t=16 mm，由式(5)求得腹板最优高度并验算支点处腹板剪力抗力是否大于支点处最大剪力Q.若腹板剪力抗力大于支点处最大剪力Q，则所得梁高即为最优梁高；若腹板剪力抗力小于支点处最大剪力Q，则以4 mm为模数适当增加腹板厚度进行迭代求解最优梁高.

建立桥宽8.5 m、主梁间距2 m，桥宽8.5 m、主梁间距3 m，桥宽41.5 m、主梁间距2 m，桥宽41.5 m、主梁间距3 m等4种简支梁模型，跨径以5 m为模数由10 m取至100 m.根据迈达斯模型得到每种桥型的最大作用弯矩M及最大剪力Q，并根据式(5)得到最优腹板高度.统计每种桥型的最优梁高并汇总得到如图2所示的活载组合梁主梁腹板高度与跨径的关系.由于组合梁桥跨境范围大都在10 m～100 m范围内，由图2可得活载组合梁桥的经济腹板高度约为跨径的1/15(跨径10 m处)～1/26(跨径为100 m处).

图2 应力控制设计时的合理主梁高度(活载组合梁桥)Fig.2 Reasonable girder height for stress control design(Live load composite girder bridge)

日本道路协会《道路桥示方书同解说-Ⅱ钢桥篇》一书(东京：丸善株式会社，2002)给出了经验公式经济梁高范围，如表1所示.

表1 日本《道桥示方书》经验公式经济梁高范围Table 1 Japan's empirical formula for economical height range of girder

2 不同跨径及类型主梁用钢量分析

对于活载组合梁,一期恒载由钢梁单独承担,二期恒载和活载由组合截面承担.分别取腹板高度为主梁跨径的1/6～1/30,将钢梁在主要荷载(一二期恒载、活载)下翼缘边缘最大拉应力控制在220 MPa左右,最大压应力也尽量靠近220 MPa;附加组合(收缩、徐变、温差效应)产生的钢梁应力控制富余强度内(55 MPa).同时桥梁板在主要组合和附加组合下产生的应力也应满足材料强度.腹板处的剪应力控制在设计值的80 %以下(即130 MPa).

图3 有限元模型建立Fig.3 Establishment of finite element model

根据上述荷载、应力水平等标准建立迈达斯杆系有限元模型(如图3所示)并进行配板，以腹板高度为参数建立跨径分别为20 m，30 m，40 m及50 m的Midas有限元模型，根据配板所得顶板、腹板、底板厚度数据得到梁宽b分别为2.5 m，3 m,3.5 m及4 m时的用钢量.由于模型建立工作量较大，模型均采用由C#程序撰写的迈达斯自动导出程序输出并使用自动配板程序进行配板工作.根据不同模型计算的对应用钢量、跨径与腹板高度之比数值，给出了不同主梁计算跨径与腹板高度之比和每平米主梁用钢量之间的关系如图4所示.

(a) 20 m 跨径(a) Span of 20 m

(b) 30 m 跨径(b) Span of 30 m

(c) 40 m 跨径(c) Span of 40 m

(d) 50 m 跨径(d) Span of 50 m

由图4可知,相同跨径的钢板梁桥用钢量随腹板高度的增加呈先上升、后下降的趋势，且不同跨径的钢板梁桥均存在一个用钢量最低的极值点.而随着主梁跨径的增加,主梁用钢量最少时主梁计算跨径与腹板高度比逐渐增大，说明主梁设计弯矩越大,主梁用钢量最少时对应的主梁高度值越大.

根据图4给出的用钢量极值点，导出与极值点用钢量相差30 %以内的腹板高度数值作为经济腹板高度范围.表2列出跨径与经济腹板高度比值的范围,括号中数字代表用钢量最少的极值点对应的跨径与经济腹板高度比值.

表2 组合结构桥梁不同跨径下经济腹板高度Table 2 Eeconomical height of girder with different spans in composite structure bridge girder

由表2可见,在不考虑顶底板厚度的情况下，随着梁宽的增加,经济梁高范围内的最小梁高也在增加.相同跨径下,不同梁宽极值点值不同是因为不同梁宽桥面板厚度不同,会对钢梁的受力产生影响.

3 推荐主梁布置方案

根据图4中用钢量极值点对应的跨径腹板高度比，得到组合结构桥梁主梁跨径为30 m,40 m,50 m,梁宽为2.5 m,3 m,3.5 m,4 m时最优腹板高度对应的用钢量，再由用钢量乘以每平米钢材成本及加工费用算得单梁造价,结果见表3.

表3 组合结构桥梁主梁单梁造价Table 3 Cost of single girder of main girder in composite structure bridge girder

对于不同跨径的简支梁桥，分析时采用的腹板高度参照表2中的经济腹板高度数据分别取主梁跨径的1/12,1/16,1/18,1/20.根据表3不同主梁宽度对应的单梁造价，根据不同桥宽下使用的主梁根数计算得到总造价，并选择不同桥宽下4种主梁类型(即梁宽为2.5 m的Ⅰ型主梁、梁宽为3.0 m的Ⅱ型主梁、梁宽为3.5 m的Ⅲ型主梁和梁宽4.0 m的Ⅳ型主梁)中造价最低的主梁布置方案(1,2,3和4)作为推荐方案,详见表4～表6.

表4 主梁跨径30m推荐方案Table 4 Recommended scheme for main beam span of 30 m

续表4

表5 主梁跨径40m推荐方案Table 5 Recommended scheme for main beam span of 40 m

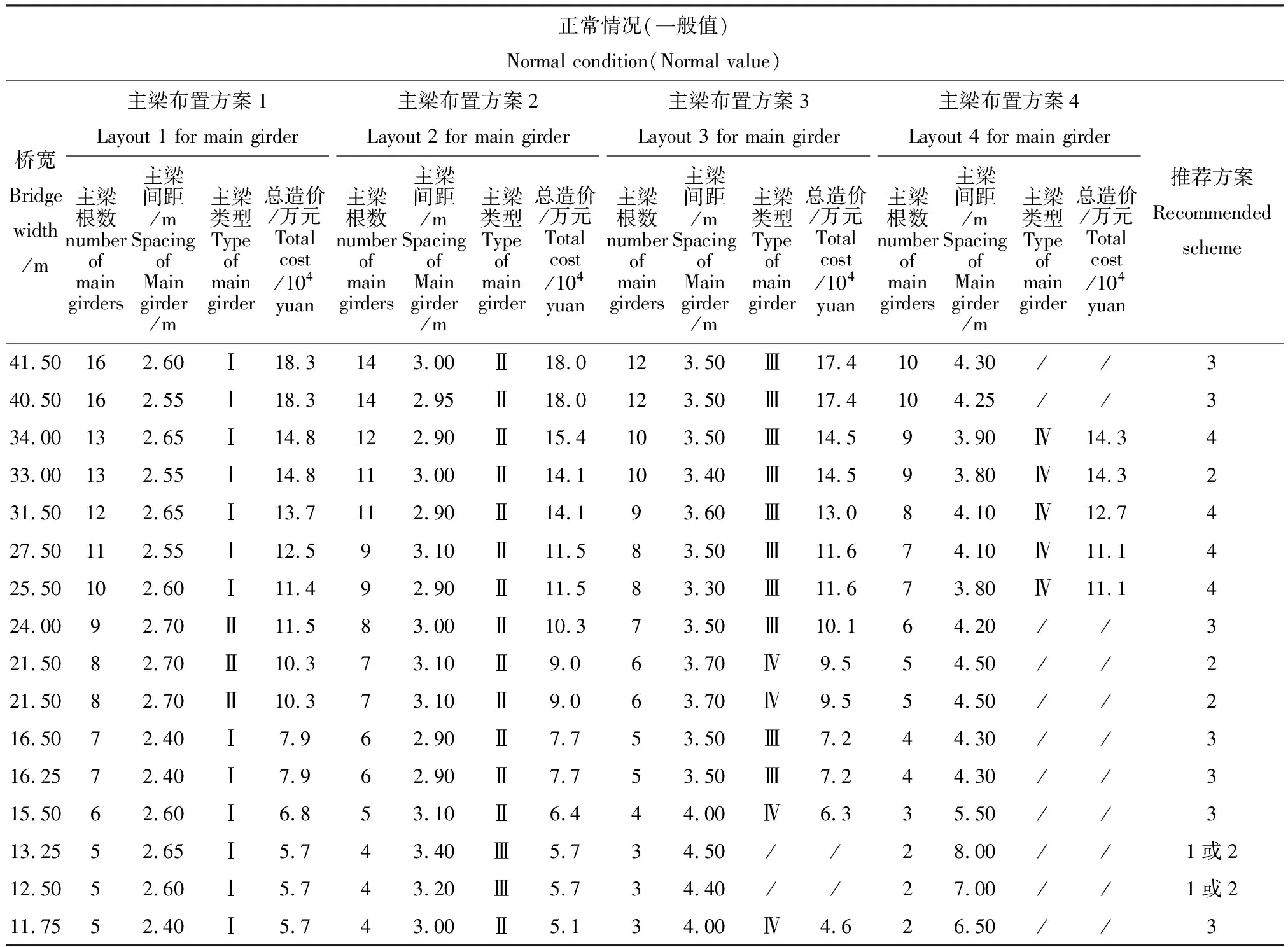
表6 主梁跨径50 m推荐方案Table 6 Recommended scheme for main beam span of 50 m

4 结语

本文分析了连续钢板组合梁桥腹板高度(近似等于梁高)与主梁用钢量的关系,由此得到了腹板经济高度(近似梁高)范围.确定腹板经济高度(近似梁高)范围后给出了组合结构桥梁主梁跨径为30 m,40 m,50 m,梁宽为2.5 m,3 m,3.5 m,4 m时的单梁造价,并选择不同桥宽下主梁宽度分别为2.5 m(Ⅰ型主梁),3 m (Ⅱ型主梁),3.5 m(Ⅲ型主梁),4 m(Ⅳ型主梁)时总造价最低的主梁布置方案(1,2,3,4)作为推荐方案.