基于神经网络的机械臂任务空间滑模同步控制

(中国石油大学(华东) 化学工程学院，山东 青岛 266580)

近年来，机械臂在工业生产、制造等领域得到了广泛的应用。目前很多任务如装配、运输、焊接等需要多个机械臂操作末端相互配合、协作形式才能完成，一个单独的机械臂无法实现这些任务[1-3]。因此，在工业应用中采取多机器人系统外部同步、互同步、协同同步或主从同步等同步策略实现协作，共同完成给定任务[4]。同时由于多机械臂的关节空间同步在工程上的应用有限，因此任务空间中的机械臂同步控制得到了越来越多的关注[5-6]。

机械臂系统是一个非线性的复杂系统，在控制过程中存在外界干扰、未建模运动学和动力学导致的不确定性。因此，建立各个单机械臂系统之间的耦合关系，准确估计不确定性，设计有效的同步控制算法是实现多机械臂任务空间同步的关键技术之一[7-10]。

针对机械臂同步控制的问题，国内外诸多研究已取得了较大进展。文献[11]针对主从机械臂的同步控制进行研究，提出一种反馈控制策略，并验证了在不同结构参数下的同步控制效果，但其反馈控制器增益对关节角度十分敏感。文献[12]提出一种空间多机械臂精准协同控制方法，实现三维空间中机械臂在追踪目标过程中对期望轨迹的跟踪，具有较高的精度和稳定性。文献[13]根据有向图理论定义新的同步误差，提出一种新的机械臂同步控制方法，可以补偿从动机械臂的不确定性并估计主动机械臂的加速度。文献[14]针对装配任务中的多机械臂协同设计了一种新的自适应同步控制算法，引入交叉耦合技术，设计的自适应控制律可以保证位置误差和同步误差同时渐近稳定。文献[15]针对存在时变通信延迟和动力学不确定性的异构机械臂系统的任务空间同步控制进行研究，并通过数值仿真和Phantom Omni机器人系统实验验证了所设计算法的有效性。文献[16]针对存在动力学和运动学不确定性的单个机械臂的轨迹跟踪问题进行研究，提出一种新的非奇异终端滑模控制算法，但未考虑多个机械臂的同步问题。尽管目前针对多机械臂同步控制的研究已经取得了很多成果，但基于图论方法的同步误差和交叉耦合误差研究还处于起步阶段，如何有效处理多机械臂系统的运动学和动力学不确定性仍需进一步探索。

在文献[16]的基础上，本研究运用滑模控制原理、神经网络算法和交叉耦合误差方法，提出了一种基于图论的多机械臂系统同步误差和交叉耦合误差算法，所设计的滑模同步控制器充分利用了滑模控制的鲁棒性和RBF神经网络的学习能力，能够在线估计运动学和动力学不确定性，提高了机械臂的同步控制精度和同步控制的鲁棒性。

1 系统描述

1.1 动力学模型

n个机械臂在任务空间中进行同步运动，完成同一操作任务的机械臂系统如图1所示。

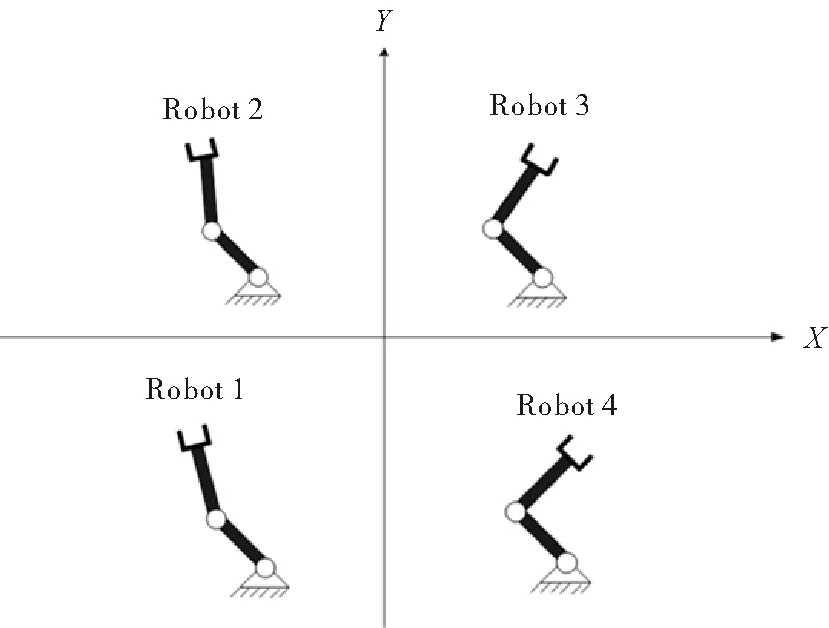
图1 多机械臂系统模型Fig.1 Multiple robotic manipulatorssystem model

运用Euler-Lagrange方法在关节空间内建立n个m关节串联机械臂动力学模型，如式(1)：

(1)

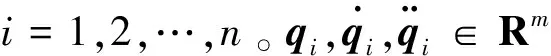
在工程应用中，大多数操作任务都是在任务空间中进行规划的，因此需要将机械臂系统动力学模型由关节空间转换到任务空间中。设xi(t)∈Rm为任务空间中的位置坐标向量，关节空间坐标可以通过式(2)转换到任务空间中：

xi=hi(qi)，

(2)

其中，hi(·)∈Rm为关节坐标空间到任务空间的转换函数。

(3)

其中，Ji(qi)∈Rm×m为关节空间到任务空间的Jacobian矩阵。

根据式(3)可以将关节空间中的机械臂系统动力学模型转换到任务空间中，如式(4)所示：

(4)

1.2 模型不确定性

由于实际机械臂系统的复杂性以及生产任务的多变性和灵活性，难以建立机械臂的精确模型，使得模型参数存在偏差。为了确保良好的控制效果和生产任务的顺利完成，在建模过程中考虑这些不确定因素是十分必要的。

(5)

其中，Mi0(·)、Ci0(·)、Gi0(·)为动力学标称项；Mi1(·)、Ci1(·)、Gi1(·)为动力学不确定性。

考虑系统的运动学不确定性，则：

(6)

将式(5)和式(6)代入动力学方程(4)，可以得到：

(7)

其中fi为模型不确定性：

1.3 同步误差

定义第i个机械臂的跟踪误差为：

ei=xid-xi。

(8)

根据无向图理论，以每个机械臂为节点，互相之间的信息传递为边，定义多个机械臂之间的连接权系数矩阵为：

其中aij=aji，且当第i与第j个机械臂有信息传递时aij=1，否则aij=0。

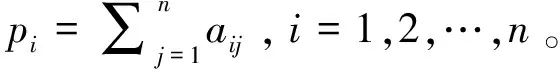
L=P-A。

机械臂系统的同步误差可以写为如下形式：

(9)

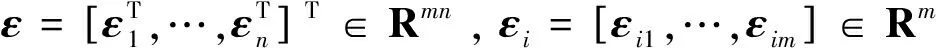
定义机械臂的交叉耦合误差：

(10)

2 同步控制器设计

由于RBF神经网络能够在线学习非线性模型[17-19]，本研究应用RBF神经网络对模型不确定性进行辨识逼近，并设计基于RBF神经网络的自适应滑模同步控制器。

2.1 滑模控制器设计

根据上节定义的交叉耦合误差(10)，定义滑模函数为如下形式：

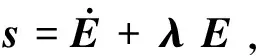
(11)

其中，λ=λT>0。

滑模趋近律定义为：

(12)

其中，正定对角矩阵K1=diag(k11,k12,…,k1n)，K2=diag(k21,k22,…,k2n)，k1i=diag(k1i1,…,k1im)，k2i=diag(k2i1,…,k2im)，i=1,…,n。趋近律可以保证系统状态在有限时间内快速到达滑模面。

机械臂动力学模型(7)可以转换为如下形式：

(13)

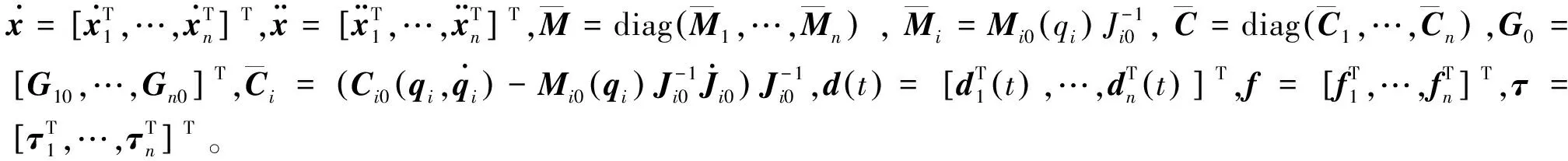
定理1如果滑模面设计为(11)，趋近律设计为(12)，在模型不确定性f=0的情况下，机械臂系统滑模控制器设计如下：

τ=τ0+τ1，

(14)

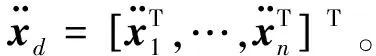
证明：选取Lyapunov函数如下：

(15)

易知，V>0。将其对时间t求导得：

(16)

(17)

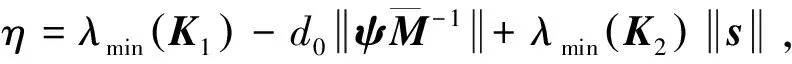
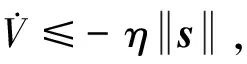
(18)

即系统状态可以在有限时间内到达滑模面。

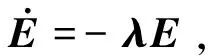
(19)

则：

(20)

由于L及ψ均为正定矩阵，由式(9)和式(10)可知，系统跟踪误差e及机械臂同步误差ε是渐近稳定的。证毕。

2.2 RBF神经网络滑模控制器设计

径向基函数(radial basis function，RBF)神经网络是一种单隐层三层前馈神经网络[20-21]。

图2 RBF神经网络结构图Fig.2 RBF Neural Network structure

其输入x与其输出y可以表示为如下形式：

(21)

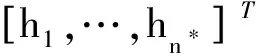
神经网络自适应律取：

(22)

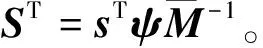
定理2如果滑模面设计为(11)，趋近律设计为(12)，在模型不确定性f≠0的情况下，自适应律设计为(22)，机械臂系统滑模控制器设计如下：

τ=τ0+τ1+τ2，

(23)

证明：选取如下Lyapunov函数：

(24)

则有：

(25)

模型不确定性f由神经网络进行估计，因此可以表示为如下形式：

f=WTh+ε，

(26)

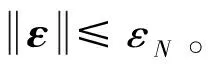
(27)

可得：

(28)

(29)

已知外界干扰及神经网络逼近误差均有界，当满足下列收敛条件时：

(30)

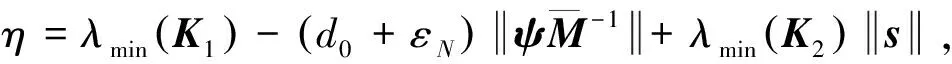
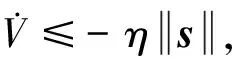
(31)

即系统状态可以在有限时间内到达滑模面。

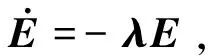
(32)

则：

(33)

由于L及ψ均为正定矩阵，由式(9)、式(10)可知，系统跟踪误差e及机械臂同步误差ε是渐近稳定的。证毕。

3 仿真验证

为验证所提出同步控制算法的有效性和稳定性，在文献[16]的基础上，设计了两个2连杆机械臂的同步仿真。

3.1 参数设定

假设所有的机械臂具有相同的动力学和运动学方程，但初始状态不同，其关节空间中的动力学方程形式如下：

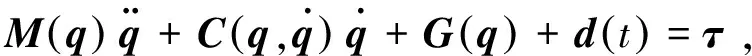
其中：

γ1(q1,q2)=(m1+m2)r1cos(q2)+m2r2cos(q1+q2)，γ1(q1,q2)=m2r2cos(q1+q2)。

关节坐标空间到任务空间的转换矩阵如下：

机械臂Jacobian矩阵为：

机械臂系统的有关参数参考文献[22]，设置如下：m1=0.5 kg，m2=1.5 kg，r1=1 m，r2=0.8 m，J1=5 kg·m，J2=5 kg·m，g=9.81 m/s2。

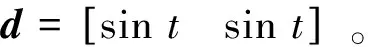
任务空间中期望轨迹设置为：

两机械臂两连杆沿x和y方向的初始位置和初始速度分别为：

控制器参数及拉普拉斯矩阵设置为：

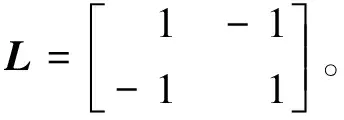
网络输入取为：

隐层高斯基函数的取值若不合适，将使高斯基函数无法得到有效的映射，从而导致RBF神经网络无效。故c按网络输入值的范围取值：

3.2 仿真结果及分析

基于上述参数进行Matlab仿真，仿真结果如图3～9所示。

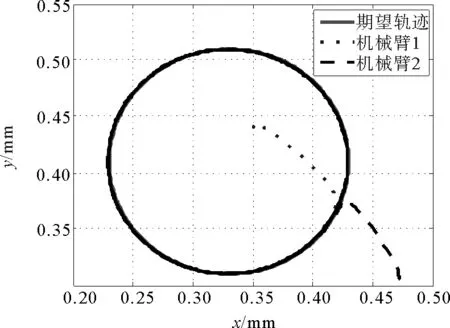
图3 任务空间中机械臂轨迹跟踪曲线Fig.3 Trajectories tracking of robotic manipulators in task space

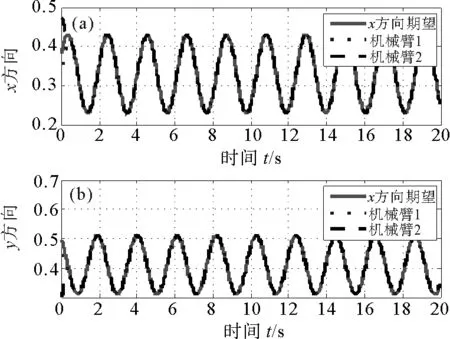
图4 机械臂x、y方向轨迹跟踪Fig.4 Movement trajectories of robotic manipulators in x and y direction

图3、图4分别为机械臂在任务空间和x、y方向上的轨迹跟踪结果。可以看出，两机械臂在同步控制器(22)的控制作用下，均能从任意初始位置精确跟踪期望轨迹，并实现同步运动，跟踪误差及同步误差可以渐近收敛到0，且整个机械臂系统在达到稳定状态后不再发生较大的波动。即模型不确定性可以被神经网络准确估计，并被控制器τ3抵消。机械臂系统的输入力矩如图5所示。

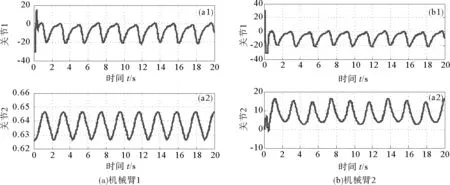
图5 两连杆机械臂关节驱动力矩Fig.5 Joint driving torque of two connecting rod manipulators

为进一步验证所设计的同步控制器的有效性，在仿真时间第10秒对机械臂1施加一个时长0.5 s的脉冲干扰，幅度为d′=25，同时以两机械臂无同步耦合时的情况为对比，仿真结果如图6～9所示。

图6 两机械臂x、y方向跟踪误差对比Fig.6 Tracking error comparison of the two robotic manipulators in x and y directions

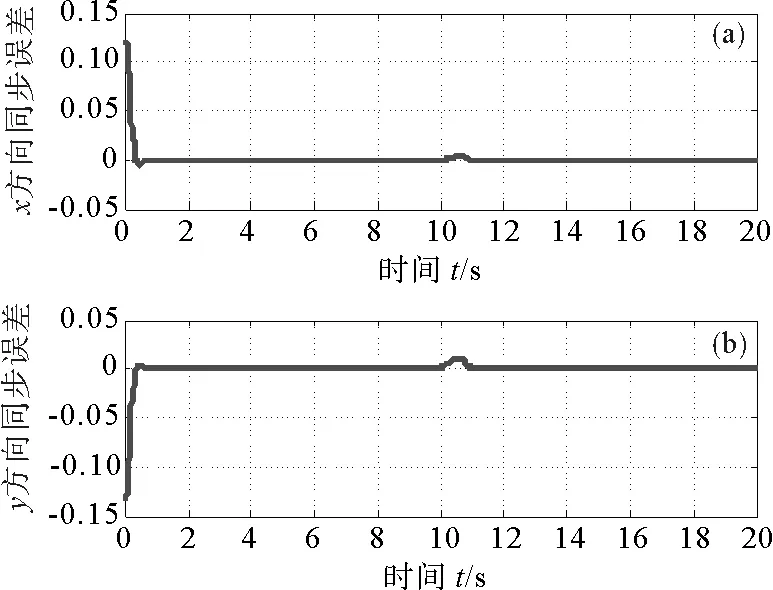
图7 两机械臂x、y方向同步误差Fig.7 Synchronization error of the two robotic manipulators in x and y directions

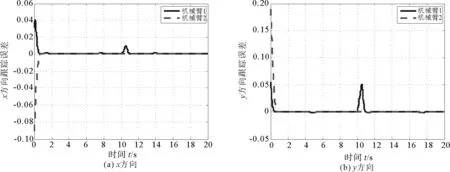
图8 两机械臂x、y方向跟踪误差对比(未同步)Fig.8 Tracking error comparison of the two robotic manipulators in x and y directions (unsynchronized)

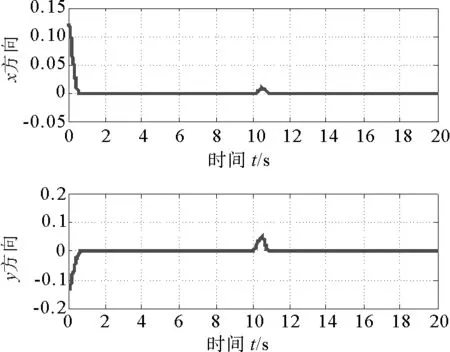
图9 两机械臂x、y方向同步误差(未同步)Fig.9 Synchronization error of the two robotic manipulators in x and y directions (unsynchronized)

图6、图7为机械臂在滑模同步控制器(23)作用下的轨迹跟踪误差和同步误差，可以看出，当机械臂1受到扰动之后，机械臂2可以快速跟踪上受扰动机械臂，同步误差保持在εx≤4.5×10-3m、εy≤0.02 m范围内。由仿真结果图8、图9可以看出，在受到脉冲干扰时机械臂1与机械臂2之间的同步误差范围为εx≤0.02 m、εy≤0.055 m，无法达到同步要求。

通过综合分析仿真结果图3～9，可以得到如下结论：通过合理设计控制器参数，利用本研究所提出的基于RBF神经网络的滑模控制算法，考虑系统存在运动学不确定性、动力学不确定性和未知干扰，且机械臂之间存在交互影响的条件下，各机械臂即使存在较大的初始误差，也能快速精确地跟踪给定轨迹，且保证机械臂在受到扰动的情况下也能实现同步运动，即本研究所提出的同步控制算法能够满足控制要求。

4 结论

本研究针对存在不确定性的多机械臂系统，对其任务空间中同步控制问题进行研究。综合运用滑模控制、RBF神经网络和交叉耦合误差等原理和方法，设计了一种新的滑模同步控制器。主要结论如下：

1) 提出一种新的基于RBF神经网络的机械臂任务空间滑模同步控制算法，可以对机械臂系统的动力学和运动学不确定性等进行估计并补偿，提高了同步控制精度及传统滑模控制器适应性。

2) 基于图论理论定义同步误差和交叉耦合误差，在此基础上所设计的滑模同步控制器可以保证机械臂在存在外界干扰的情况下实现同步运动。