视频背景分离中一种新的非凸秩近似的RPCA模型

(山东科技大学 数学与系统科学学院 ，山东 青岛 266590)

1 引言

随着监控设备的普及，监控视频在社会管理和安全中发挥着重要的作用。这些视频信号往往是大规模带有噪声的数据，给数据分析带来了困难。监控视频信号的自动识别已成为目标追踪、交通检测以及场景分析等领域的关键环节。其中，如何有效地从视频帧序列中分离出背景和移动前景受到学者的广泛关注。

2006年，Donoho等[1]提出了压缩传感(compressed sensing)理论，认为高维信号在某个变换域上具有稀疏性，可以以很大的概率从较少的线性测量信号中高维信号恢复出来。之后基于压缩传感理论的秩极小化技术被广泛应用于高维数据分析及图像处理领域。

为了对视频序列的前景与背景进行有效分离，学者们把矩阵秩的极小化技术引入主成分分析(principal component analysis，PCA)模型[2]。大量数值实验结果表明，当观测矩阵只含较小的高斯随机噪声时，PCA模型可以准确地分离出视频序列的前景与背景。考虑到PCA模型对于含有异常值或者尖锐噪声的观测数据非常敏感，且不适用于带有稀疏噪声的矩阵，Candes等[3]提出了鲁棒主成分分析(robust principod component analysis,RPCA)模型，在原有的模型中加入矩阵稀疏表示，并利用交替方向法对模型进行求解。实验结果表明，RPCA模型对数据矩阵的噪声更加稳健。目前，RPCA模型已被广泛应用于视频前景提取[4]、人脸识别[5]和图像对齐[6]等领域。

传统的RPCA模型可描述为如下优化问题：

(1)

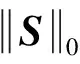
(2)

对于模型(2)，为了降低求解模型的计算时间，提高处理效果，Lin等[7]提出了IALM(Inexact augmented Lagrange multipliers)模型，在RPCA模型中加入了低秩稀疏矩阵的正则项，并利用非精确拉格朗日乘子法求解提出的模型，大幅度降低了运算时间。Zhou等[8]采用双边随机投影模型，利用投影算子代替奇异值分解(singular value decomposition,SVD)，提出了Go分解(go decomposition，GoDec)模型，提高了图像的处理效果。上述方法均基于核范数近似的RPCA改进模型，但由于核范数是对秩函数的有偏估计，当矩阵出现过大奇异值时，会出现核范数的秩估计过大问题，导致图像处理效果不理想，且模型求解的每一步都要对矩阵进行奇异值分解，随着问题规模增加，计算时间也会大幅度增加。因此，很多学者开始尝试利用非凸函数近似秩函数[9-11]，数值实验结果表明，用非凸函数近似秩函数的效果更优。

另一方面，传统的RPCA模型通常采用矩阵的L1范数来描述图像整体的稀疏性。但由于L1范数未考虑前景像素之间的相关性以及空间上的连续性，使分离效果受到很大的影响。许多学者进而考虑用矩阵的L2,1范数来代替L1范数，与L1范数的稀疏性要求不同，L2,1范数在要求整体稀疏的同时还要求列稀疏，以充分考虑稀疏项元素之间的相关性，更好地分离运动前景[12]。

针对核范数的缺陷以及非凸秩近似函数所展现出的良好特性，提出一种新的非凸函数来近似秩函数，同时利用矩阵的L2,1范数来近似L0范数，得到一个改进的RPCA模型，采用增广拉格朗日交替方向法求解该模型，并将该模型应用于视频背景分离。数值实验结果表明，与核范数及现有的非凸近似模型相比，提出的非凸函数及非凸秩似模型具有更好的数值效果及鲁棒性。

2 改进的RPCA模型

文献[13]对目前的主流非凸秩近似函数特征进行了分析，要求非凸秩近似函数要满足矩阵范数的一般性质，且具有良好的秩近似效果。为更好地近似秩函数，提高RPC模型的数值计算效率，本研究提出一个新的非凸函数来近似秩函数，进而得到一个改进的RPCA模型NC-ALM(non-convex Augmented Lagrange method)模型。

考虑如下非凸函数

(3)

其中，g(x)为[0,∞)上的增函数，t为模型参数。

定义非凸秩近似函数

(4)

其中，σi(L)为L的第i个奇异值。

由文献[13]，可得如下结论：

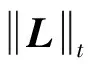
2) 当σi(L)=0时，g(σi(L))=0；

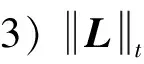
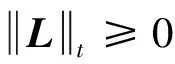
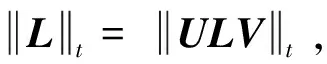
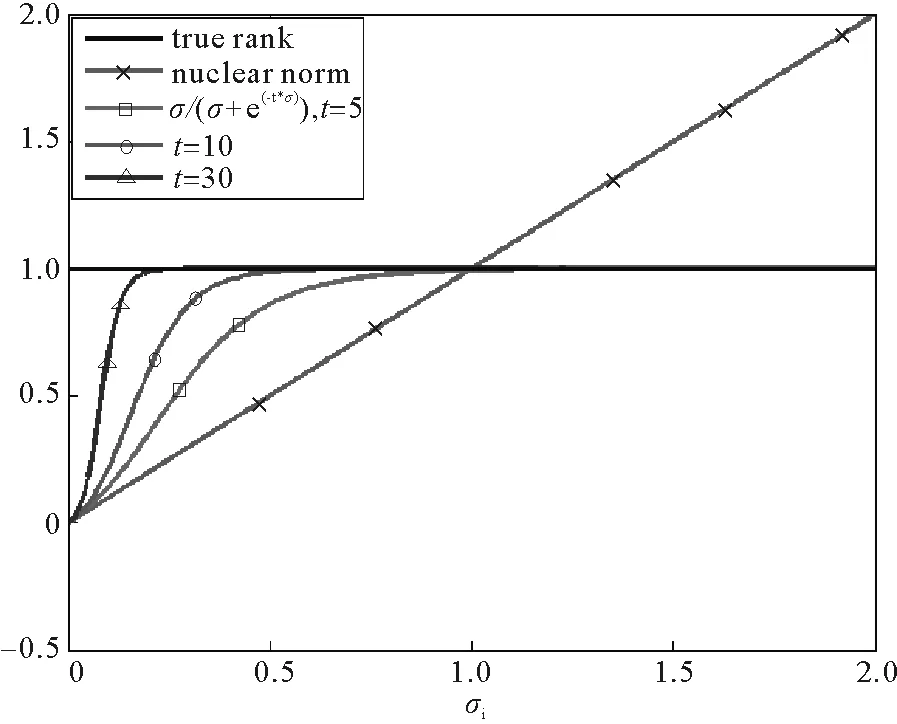
图1 秩近似函数与核范数对比图Fig.1 Comparison of rank approximation function and nuclear norm

为了更加直观展示提出的非凸函数的性质，图1给出了近似函数对秩的近似效果，可以看出，当矩阵奇异值为0时，提出的非凸函数值为0；当矩阵的奇异值大于0时，该函数会快速的逼近于1；而当矩阵奇异值增大时，该函数值会稳定的逼近于1。而随着参数t取值增大，该函数会更加迅速地逼近真实秩。因此，该非凸秩近似函数的近似效果要优于核范数。

3 增广拉格朗日乘子法

(5)

本节利用增广拉格朗日交替方向乘子法，来求解模型(5)。

模型(5)的增广拉格朗日函数为：

(6)

其中，〈A,B〉=Trace(ATB)表示两个矩阵的内积，Y是拉格朗日乘子，μ是正则参数。

给定初始的L0以及Y0，增广拉格朗日交替方向乘子法的求解框架如下：

(7)

(8)

Yk+1=Yk+μk(Lk+1+Sk+1-X)，

(9)

μk+1=ρμk。

(10)

3.1 求解问题(7)

对于子问题(7)的求解，有如下结论：

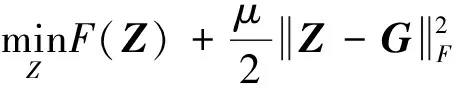
(11)

问题(11)是一个凹函数与凸函数的组合，利用文献[15]的算法进行求解可得

(12)

式(12)的封闭解

(13)

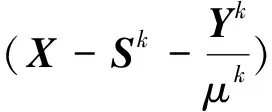
Lk+1=Udiag(σ*)VT。

(14)

3.2 求解问题(8)

S的更新可以通过文献[16]的引理3.3进行计算。

引理3[16]对于给定的矩阵M∈Rm×n以及τ>0，则优化问题：

存在唯一的封闭解S*。那么 ：

(15)

其中Mj表示矩阵M的第j列。

由上述结论可得求解问题(5)的算法框架如下：

算法1: 非凸增广拉格朗日乘子法(NC-ALM)输入: 观测矩阵X,参数λ,μ>0,最大迭代kmax; 初始化: S=0,Y=0,迭代次数k=0; 步骤1:利用式(14)更新Lk+1; 步骤2:利用式(15)更新Sk+1; 步骤3:计算 Yk+1=Yk+μk(Lk+1+Sk+1-X); 步骤4:计算 μk+1=ρμk; 直到k>kmax或{Lk,Sk,Yk}收敛;输出:L=Lk+1,S=Sk+1。

4 实验结果与比较

本节将提出的NC-ALM模型应用到不同的场景中，包括静态/动态背景下的背景前景分离，并与APG[17]，IALM和GoDec 3种模型进行比较。4种模型用到的数据集以及运行环境相同，数值实验均基于PC Intel Core i3-3240T 2.90GHz CPU,4GB RAM环境，使用MATLAB R2014a实现。

4.1 参数设置

NC-ALM模型中主要用到4个参数：μ、λ、ρ以及t。参考文献[18]中的λ取值规则，取λ=10-3。对于惩罚参数μ，采用逐步递增的方式，并取初始值μ0=2.4×10-5。为了加快算法收敛速度，参数ρ=1.2。t为非凸函数的参数，实验中取t=300。

算法迭代停止标准为：

Err≤εor Iter≥Imax，

(16)

其中

(17)

ε为预先输入的终止误差，ε=10-6，Iter为当前的迭代次数，Imax为预先输入的最大迭代次数，Imax=300。

4.2 实验比较

实验采用了12R数据集，其中包括Hall、Escalator、Lobby、Fountain、Campus和Restaurant视频集。对于用到的每个视频序列，截取了连续的几百帧作为观测数据集。

表1 实验中的数据集统计信息
Table 1 Statistical information of data sets in the experiment

数据集图像维数数据集帧数截取数据集帧数Hall144∗1763 584100Escalator130∗1603 000100Lobby128∗1602 000100Fountain128∗1602 750170Campus 128∗1601 439210Restaurant120∗1603 055500

为了使不同的算法具有可比性，实验统一采用APG算法的停机准则。GoDec模型需要预先设置矩阵的秩，根据文献[8]，秩设置为5。表2给出了4种模型处理不同数据集的迭代次数以及运行时间对比。无论在动态背景还是静态背景的数据集中，由于GoDec模型采用随机投影的方式，难以保证计算精度，故迭代次数固定为101。而APG模型需要迭代100次以上，IALM模型需要迭代32次，本模型需要迭代3到5次。由于迭代次数远低于其他三种模型，NC-ALM模型的运行时间最短。因此在处理大规模的数据信息时，NC-ALM模型优势更大。

表 2 模型迭代次数与运行时间比对Tab.2 Comparison of model iteration number and running time

表 3 算法恢复背景矩阵秩与计算误差对比Tab.3 Comparison of model recovery background matrix rank and calculation error

表3给出了4种模型恢复出低秩矩阵的秩以及计算精度比较。由于监控设备是固定的，视频背景相对固定，因此每一帧的背景像素大致相同，真实低秩矩阵的秩为1。通过表3可以看出，APG模型的秩大大偏离了真实低秩矩阵的秩，GoDec模型由于添加了秩约束，恢复的低秩矩阵秩固定为5,而本文的NC-ALM模型恢复的低秩矩阵最接近真实的背景矩阵秩。特别在Restaurant数据集中，视频中移动目标移动缓慢，APG模型以及IALM模型将部分本属于前景中的像素归类于背景中，导致背景矩阵的秩远远高于真实秩，而NC-ALM模型可以很好地恢复出矩阵的真实秩。此外，NC-ALM算法的计算精度高于GoDec以及APG模型。

图2为视觉效果比较，第一行至第六行分别为Hall、Escalator、Lobby、Fountain、Campus和Restaurant视频集。第1列是六个数据集中选取的某一帧原始图片；2～3列是APG模型恢复的背景前景图片；4～5列为IALM模型恢复的背景前景图片； 6～7列为GoDec模型恢复的背景前景图片；8～9列为本文模型恢复的背景前景图片。由图2对比可以看出，在Escalator和Restaurant数据集中，APG、IALM、GoDec模型都存在将前景像素归类于背景的情况，导致恢复的背景不清晰(背景图像中残留了移动目标的阴影)。 特别是Restaurant视频集，APG、IALM模型将大量前景像素归类于背景，GoDec模型存在少量阴影，而NC-ALM模型分离出了更为干净的背景。

在图3中以Escalator数据集为例给出了4个模型的像素值对比，用纵坐标表示Escalator数据集每一帧中的坐标(36,55)的像素值，横坐标表示帧数。Escalator数据集的横坐标分为4个区间，分别是[0,13],[14,29],[30,40],[41,100]。第1个区间中，人即将出现，影子先到达了标记的坐标；第2个区间中，人出现在标记的坐标上；第3个区间，人刚离开，影子出现在了该坐标上；第4个区间中的坐标为背景，没有移动物体。从图3可以看出，在人即将经过的第1个区段[0,13]帧以及人刚经过、但留有影子的第2个区间[30-40]帧，APG，IALM，GoDec背景像素值接近原始帧的像素，说明并未检测出影子。而本文算法在这2个阶段更接近于真实的背景像素；在人经过标记点的第二个区间[14-29]帧，GoDec跟IALM比较接近真实背景像素值，但本模型恢复效果更好。

图2 不同模型视频背景分离效果比较Fig.2 Comparison of background separation effect for different models

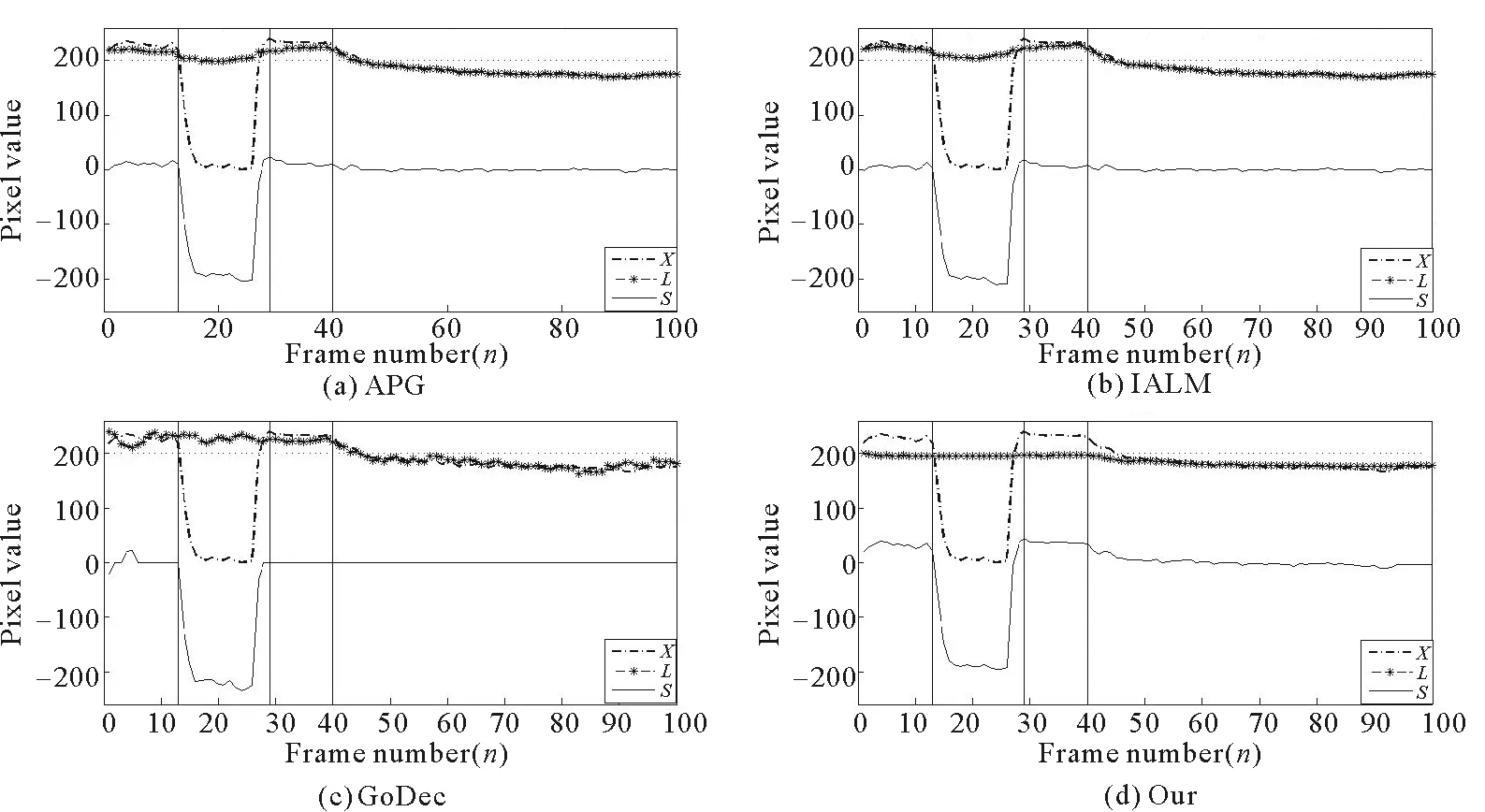
图3 Escalator数据集像素值对比

从图3中有人经过的3个区间中各选取了一帧，即视频序列的第1帧、第20帧和第30帧进行比对，得到图4。可见，GoDec、IALM和APG模型提取的背景含有前景像素的干扰(框内部分)，而本算法恢复了干净的背景。

5 结论

为了改进传统RPCA模型中核范数近似秩函数存在的秩估计过大且计算效率低下缺陷，设计了一种新的非凸函数近似秩函数，并且采用了结构性稀疏的模型，以在保证稀疏约束的前提下，考虑运动目标在空间上的相关性，得到了一种新的非凸秩函数PCA模型NC-ALM。从实验定量分析来看，NC-ALM模型在保证精度的前提下，减少了运算时间，提高了图像处理的效果。且随着数据规模的扩大，NC-ALM模型具有更好的应用前景。