卫星装备体系贡献度评估*
刘翔宇,张裕,赵洪利,杨海涛
(航天工程大学a.研究生管理大队;b.航天遥感实验室,北京 101416)
0 引言
随着信息化战争的发展,天基信息支援武器装备与系统之间的交链耦合性越来越强,对作战的影响程度越来越大,因此,很有必要探索如何评估量化天基信息支援装备的体系贡献度。
体系贡献度是我军的首创概念,国外相关研究很少,国内学者近两年做了大量尝试。文献[1-5]针对装备体系贡献度的概念,进行了较为详细的论述,舒宇将体系贡献度定义为武器装备对特定使命任务的需求满足程度,基于能力与权重值对武器装备的体系贡献度进行评估[6];罗小明从任务、能力、结构、演化4个维度来探讨体系贡献度的内涵和分类,构建武器装备体系贡献度分析的总体框架[7];金从镇通过OODA作战过程构建作战效能评估指标体系,基于作战效能对海军装备体系贡献度进行评估[8];叶子晴基于规则推理技术,阐述了海军航空作战装备体系贡献度的评估方法[9],周鼎基于模糊数学的方法,对天基武器装备体系贡献度进行评估[10]。
在现有研究中,对天基信息支援装备的体系贡献度研究较少,且多以某一作战任务为背景,直接对装备体系贡献度构建指标体系进行评估。现代信息化作战中体系内部各装备之间关系复杂,构建指标体系难免会有一些疏漏。兰彻斯特方程作为经典作战分析模型,能够较好的规避体系内各系统与装备之间的复杂联系。大量学者对兰彻斯特方程进行了研究,并取得了很多研究成果[11-16]。
本文通过改造方程,计算方程仿真后输出的双方兵力变化曲线与坐标轴围成的面积,分析比较不同天基信息支援装备的体系贡献度,确定了实际中应采用的装备支援方案。
1 基本概念阐述
1.1 梅特卡夫定律
梅特卡夫定律(Metcalf′s Law)是一种网络技术发展规律,他的缔造者是以太网协议技术发明者、3Com公司创始人罗伯特·梅特卡夫,其主要内容是:网络的价值等于网络节点数的平方,网络的价值与互联网的用户数的平方成正比。其公式为
V=k·N2,
(1)
式中:k为价值系数;N为用户数量。
定律表示,网络价值与用户数量的平方成正比,网路使用者越多,价值就越大,即网络的价值与网络规模的平方成正比。
梅特卡夫定律[17]将网络的价值与网络规模结合起来,并建立计算模型,这在军事领域也产生了重大影响。信息化战争中,天基信息支援条件下的各作战武器装备的态势共享起着军队战斗力倍增器作用。故可以利用梅特卡夫定律与军队战斗力生成因素进行合理映射,构建天基信息支援下的作战模型。
1.2 兰彻斯特方程
1914年,兰彻斯特在其名著《战争中的飞机:第四个兵种的出现》中首次提出了作战损耗定量分析的兰彻斯特方程。兰彻斯特方程是一组描述交战双方作战力量损耗的微分方程,可以用来对作战过程进行各种预测。
当前,兰彻斯特方程最基础的形式为兰彻斯特第一线性定律、兰彻斯特第二线性定律[18]、兰彻斯特平方定律[19]。
兰彻斯特第一线性定律是以古代战斗模型为基础得出的。其假定条件是作战兵力相互暴露;战斗由单个战斗成员之间一对一的格斗组成,其数学模型为
(2)
兰彻斯特第二线性定律是根据远距离战斗的模型得出的,其假定条件是双方兵力互相隐蔽,每一方火力集中在对方战斗成员的集结地区,其数学模型为
(3)
兰彻斯特平方律建立在近代战斗模型的基础上,这里基本假设双方兵力相互暴露;每一方可运用他们全部兵力并集中火力射击对方兵力,其数学模型为
(4)
式中:r(t),b(t)为红方、蓝方在t时刻的兵力数量;α,β为红方、蓝方的损耗系数。
1.3 体系贡献度
本文在基于文献[1,4]对体系贡献度进行分类的基础上,认为装备的体系贡献度具有相对性,必须要有一个比较的对象,是一个相对的概念。依据装备的有无与改进2种不同情况,提出对己体系增益贡献度、对敌体系抑制贡献度,其中每一种贡献度又分为绝对体系贡献度和相对体系贡献度(贡献率),如图1所示。
1.4 军用卫星支援体系
天基信息支援体系[20-25]包含军用卫星系统、应急发射系统以及站网支援系统,其总体结构如图2所示。
(1) 军用卫星系统
军用卫星系统包括通信中继卫星系统、导航定位卫星系统、侦察监视卫星系统。在谋求夺取信息优势,实现信息主导的一体化联合作战中,侦察卫星系统提供了可靠的目标识别和毁伤评估,以及测绘、气象保障;通信中继卫星系统提供了有效的信息传输分发和指挥控制保障;导航定位卫星系统提供了精确的目标定位和武器制导保障。
(2) 应急发射系统
应急发射系统主要由各类航天器发射系统以及航天器维修保障系统组成,主要用于维持战时各军兵种对通信、侦察、以及导航的天基信息支援能力的需求,缩短已被破坏的系统的恢复时间,为作战赢取时间。
(3) 站网支援系统
站网支援系统主要是由地面站以及相关设备组成,用于实时监控卫星的位置,上注卫星指令,并对卫星获取的情报信息进行综合集成,实现快速接收与分发。
2 梅特卡夫-兰彻斯特方程建立
2.1 数学模型
通过分析兰彻斯特第二线性定律和兰彻斯特平方律,结合天基信息支援装备给作战带来的信息互通与共享作用,融合梅特卡夫定律,可以认为,当红蓝双方均获取天基信息支援,双方作战武器装备之间可以实现信息互通与共享,实现对战场态势的完全感知,其攻击属于直接瞄准,战斗力呈指数级增长,满足兰彻斯特平方律与梅特卡夫定律;当双方均没有天基信息支援或双方天基信息支援能力不够时,作战武器装备之间不能实现信息互通与共享,不能实现对战场态势的完全感知,其攻击属于间接瞄准,战斗力不能呈现指数级增长,不满足梅特卡夫定律,但满足兰彻斯特第二线性定律。
考虑航天侦察任务流程、天基信息支援的开始时间、天基信息支援能力,天基信息支援后实现信息互通和态势共享的作战装备比例系数,结合梅特卡夫定律,建立能够描述天基信息支援条件下红蓝双方兵力变化的梅特卡夫—兰彻斯特方程,其表达式如下:
0≤λr≤1,0≤λb≤1,0≤Ir≤1,0≤Ib≤1,
(5)
式中:α,β为红方、蓝方单兵(武器装备)的平均作战效能[26];Ir,Ib为红蓝双方的天基信息支援能力;λr,λb为红蓝双方获得天基信息支援后实现信息互通与态势共享的装备比例;tr,tb为红蓝双方的天基信息支援开始时间;ε(t)为阶跃函数,用它来表示只有当航侦任务流程完毕,天基信息支援时间开始时,天基信息支援力量才能够加入。
2.2 参数度量
(1) 天基支援开始时间t
天基信息支援开始时间即航侦任务完成的时间。主要包括支援需求提交与资源监控筹划时间t1、支援计划制定与指令上注执行时间t2、信息汇集接收与数据处理时间t3、支援产品筛选与态势按需保障协同时间t4。以红方支援开始时间为例:
tr=tr1+tr2+tr3+tr4.
(6)
(2) 天基信息支援能力I
依据天基信息支援体系的组成,天基信息支援能力主要包括通信能力I1、导航能力I2、侦察能力I3、站网支援能力I4、应急发射能力I5。ω1~ω5为各能力的权重分配值。以红方天基信息支援能力为例:
Ir=ωr1Ir1+ωr2Ir2+ωr3Ir3+ωr4Ir4+ωr5Ir5.
(7)
(3) 装备互通比例λ
以红方装备互通比例为例:
(8)
(4) 对已体系增益贡献度、对敌体系抑制贡献度
若装备A从无到有,则装备A的对己增益绝对体系贡献度为VA,相对体系贡献度为VB,对敌抑制绝对体系贡献度为VC,相对体系贡献度为VD;若装备B改进为装备A,则装备A对己增益绝对体系贡献度(相对B)为VE,相对体系贡献度(相对B)为VF,对敌抑制绝对体系贡献度(相对B)为VG,相对体系贡献度(相对B)为VH。
当装备A从无到有时,对己体系增益绝对贡献度表达式为
VA=SrIA-SrNIA.
(9)
对己体系增益相对贡献度(贡献率)为
(10)
对敌体系抑制绝对贡献度为
VC=SbIA-SbNIA.
(11)
对敌体系抑制相对贡献度(贡献率)为
(12)
当使用同类型、性能更好的的装备A替换装备B,相当于对装备B进行改进,此时对己体系增益绝对贡献度为
VE=SrIANIB-SrIBNIA.
(13)
对己体系增益相对贡献度(贡献率)为
(14)
对敌体系抑制绝对贡献度为
VG=SbIANIB-SbIBNIA.
(15)
对敌体系抑制相对贡献度(贡献率)为
(16)
式中:SrIA为仅含装备A时红方的仿真曲线与坐标轴围成的面积;SrNIA为不含装备A时红方仿真曲线与坐标轴围成的面积;SbIA为仅含装备A时蓝方的仿真曲线与坐标轴围成的面积;SbNIA为不含装备A时蓝方仿真曲线与坐标轴围成的面积;SrIANIB为含装备A、不含装备B时红方的仿真曲线与坐标轴围成的面积;SrIBNIA为含装备B不含装备A时红方仿真曲线与坐标轴围成的面积;SbIANIB为含装备A、不含装备B时蓝方的仿真曲线与坐标轴围成的面积;SbIBNIA为不含装备A、含装备B时蓝方仿真曲线与坐标轴围成的面积。
3 卫星装备体系贡献度评估示例
战时,侦察卫星系统获取敌方及周边地区兵力部署变动情况以及作战区域内战场态势等情报信息,提供敌目标的精确位置,供飞机和导弹攻击,为决策指挥提供依据。侦察卫星装备的性能直接影响情报产品的生成速度与航侦任务的完成时间,故可认为侦察卫星装备性能的高低可影响天基信息支援能力与天基信息支援开始时间;导航卫星主要对各作战单元进行定位、导航、制导与精准授时,可认为导航卫星装备性能的高低仅影响天基信息支援能力;通信卫星能够为各作战单元提供一体化通信服务,通过数据链分发传输各指挥机构间的作战信息、侦察情报信息等内容,可认为通信卫星装备性能的高低可影响天基信息支援能力与天基信息支援开始时间,特此说明。
3.1 想定案例描述
针对梅特卡夫-兰彻斯特方程,设计作战想定案例条件如下:
通过调整侦察卫星支援方案,改变天基信息支援开始时间与天基信息支援能力的案例想定条件:先期,蓝方具有兵力优势,红方采用支援方案1,仅有导航卫星与通信卫星支援,无侦察卫星,天基信息支援开始时间稍早于蓝方,红蓝双方的天基信息支援能力与装备互通比例基本相同;随后,红方采用方案2,用侦察卫星1加强侦察,红方信息支援开始时间提前,信息支援能力有所提高;最后,红方采用方案3,用侦察能力最强的侦察卫星2替换侦察卫星1,信息支援开始时间进一步提前,信息支援能力进一步提高,各方案卫星组成如表1所示。
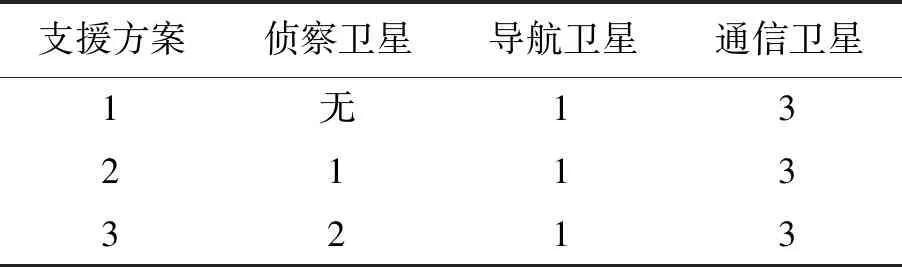
表1 调整侦察卫星的各支援方案Table 1 Adjustment of support schemes for reconnaissance satellites
3.2 仿真参数设置与结果分析
参照文献[12],为检验方程的有效性以及比较不同性能的侦察卫星装备对作战进程的影响程度与对作战体系的贡献度,可依据实际情况,合理对参数进行数值设置。方程中参数的数值标准与具体计算方法可参照文献[6-8,11],特此说明。
方案1:红方初始兵力为70,天基信息支援开始时间为5,天基信息支援能力为0.8,装备互通比例为1;蓝方初始兵力为100,天基信息支援开始时间为7,天基信息支援能力为0.5,装备互通比例为1。
方案2:红方初始兵力为70,天基信息支援开始时间为4.5,天基信息支援能力为0.85,装备互通比例为1;蓝方初始兵力为100,天基信息支援开始时间为7,天基信息支援能力为0.5,装备互通比例为1。
方案3:红方初始兵力为70,天基信息支援开始时间为4,天基信息支援能力为0.95,装备互通比例为1;蓝方初始兵力为100,天基信息支援开始时间为7,天基信息支援能力为0.5,装备互通比例为1。
将参数代入方程进行仿真,得到不同天基信息支援方案下红蓝双方的兵力变化如图3~5所示。
图3~5中的纵坐标代表双方剩余的兵力数量,横坐标描述的作战时间表示广义的时间单位(仅表示时间数字的大小),实际时间大小在微分方程模型中的时间量度给定以后可确定。
由仿真结果可知,当红方未使用侦察卫星时,由于侦察能力不够,致使天基信息支援的开始时间较晚,最终红方全军覆没,未取得战争的胜利(数量为0即为失败);当红方调整信息支援方案,使用侦察卫星1与侦察卫星2时,信息支援能力得到增强,天基信息支援开始时间提前,红方最终取得胜利。
对所得曲线面积进行积分,可得:S1为285.32,S2为50.43,S3为333.25,S4为42.834,S5为148.13,S6为197.26。
与方案1进行对比,侦察卫星1的对己体系增益绝对贡献度为
VA=S5=148.13,
对己体系增益相对贡献度为
对敌体系抑制绝对贡献度为
VC=S1=285.32,
对敌体系抑制相对贡献度为
与方案2相比,侦察卫星2的对己体系增益绝对贡献度为
VE=S4=42.834,
对己体系增益相对贡献度为
对敌体系抑制绝对贡献度为
VG=S2=50.43,
对敌体系抑制相对贡献度为
通过对案例进行仿真分析表明:未来战争中,侦察监视能力在战争中表现出非凡的功效,通过对侦察卫星装备的合理运用,能够提高天基信息支援能力,帮助我军获取制天权,提高战斗力,掌握战争主动权。
4 结论
(1) 建立了天基信息支援作战的数学模型,考虑天基信息支援作战的特点,结合天基信息支援时间、天基信息支援能力、装备互通比例,基于梅特卡夫定律,将兰彻斯特第二线性定律、兰彻斯特平方律相结合,建立了表示双方作战单位数量变化的微分方程模型,在一定程度上反映了天基信息支援力量的战斗力倍增器作用。
(2) 提出了基于微分方程仿真输出的兵力变化曲线面积来计算装备体系贡献度的方法,针对侦察卫星装备,设计对抗试验,并计算装备的体系贡献度。得出的结论为性能不同的侦察卫星装备的体系贡献度不同,对作战进程的影响程度也不同。侦察卫星装备的性能越强,体系贡献度越大,对作战进程的影响程度越深。实验结论为天基信息装备支援方案的筹划与决策提供了依据,为今后开展相关研究提供了一种新思路。
下一步研究中,将在双方多军兵种联合作战的对抗条件下,将微分方程多元化,针对受支援的不同军兵种武器装备,合理筹划多颗不同类型的卫星装备支援作战,深入研究数学对抗模型,分析不同支援装备在不同支援方案下对不同军兵种的体系贡献度。

