改进非等间距GM(1,1)-BP模型的导弹退化状态预测*

徐廷学，刘崇屹，朱桂芳，唐玲，刘沛纹

(1.海军航空大学,山东 烟台 264001；2.中国人民解放军92957部队，浙江 舟山 316000； 3.中国人民解放军92095部队，浙江 台州 318050)

0 引言

导弹系统中某些部件的性能退化是影响导弹作战效能的关键因素。利用导弹部件的相关状态信息准确预测其状态发展趋势，在故障发生前进行有计划的科学合理的维修，可以克服传统维修方式带来的“维修过剩”和“维修不足”等问题，对提高导弹的战备完好性具有十分重要的意义。

导弹在贮存状态下的测试数据往往是不等时间间隔的[1]。在进行导弹退化状态的预测时，传统非等间距灰色模型因其对趋向性数据的预测优越性而得到广泛的应用[2-4]，然而由于该模型的自身局限性问题，在数据适应性和预测精度方面往往达不到人们的期望。王大鹏[5]针对传统灰色模型在中长期预测中精度不高的问题，通过缓冲算子对数据进行预处理，强化了发展趋势，提高了精度，但是预测精度的改善有限。孔垂猛[6]将灰色模型与马尔可夫模型相结合，使模型序列更适用于波动性较强的数据序列预测，却是以牺牲预测精度为代价的。吴利丰[7]对离散灰色模型进行了改进，提高了预测精度，但是算法较为复杂。考虑到BP神经网络在处理随机性和非线性数据时有很大的优势[8-9]，可以填补灰色模型难以把握波动性较大等非线性复杂问题的缺陷，因此，将BP神经网络与灰色模型相结合，以期实现二者的优势互补，提高数据适应性和预测精度。

基于以上分析，本文提出了一种基于改进非等间距GM(1,1)-BP模型的导弹退化状态预测方法。首先，提出一种权值搜索的背景值构造方法，然后以原始序列和拟合序列的一次累加生成序列的平均相对误差绝对值最小为目标对初始条件进行优化，结合新陈代谢思想实现对传统非等间距GM(1,1)模型的改进，减小拟合误差，提高模型精度。进而构造灰色模型拟合值与实际值的差值序列，最后采用滚动预测法建立差值序列的BP神经网络预测模型，还原得到最终预测值。通过导弹的预测实例对本文提出模型的预测性能进行验证。

1 改进非等间距GM(1,1)模型的构建

1.1 传统非等间距GM(1,1)模型的建立

设原始序列X(0)(ti)={x(0)(t1),x(0)(t2),…,x(0)(tn)}，时间间隔Δti=ti-ti-1(i=2,3,…,n)不等于常数，则序列X(0)(ti)为非等间距序列。

若X(0)(ti)与X(1)(ti)满足准光滑性检验、准指数规律检验和级比检验，则X(1)(ti)序列具有指数增长的规律，即满足一阶线性微分方程：

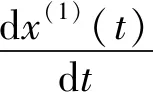
(1)

称为模型的白化微分方程。

对应的灰微分方程为

x(0)(ti)Δti+az(1)(ti)=bΔti,

(2)

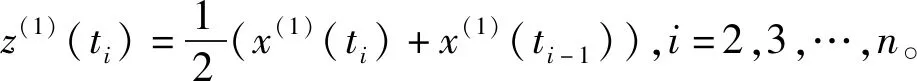
参数a和b的最小二乘估计为

式中：

若规定x(1)(t1)=x(0)(t1)，则白化微分方程的时间响应函数为

(3)

(4)

1.2 非等间距GM(1,1)模型的优化

1.2.1 误差原因分析

根据非等间距GM(1,1)模型的建模过程可知，非等间距GM(1,1)模型的模型精度与发展系数a与灰色作用量b以及待定常数c的选取有关。其中，a和b取决于原始序列和背景值的构造；计算c时，是以x(1)(t1)=x(0)(t1)为前提条件的，事实上二者并不一定相等，因此需要对初始条件进行优化。

1.2.2 权值搜索的背景值优化

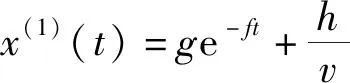
由此受到启发，在非等间距GM(1,1)模型(图2)的构造过程中，将时间间隔因素Δti考虑进来，仍用梯形面积abcd近似计算背景值：

(5)

显然，存在当曲线急剧增长造成的偏差ΔS过大的问题，此外，由于x(1)(ti)和x(1)(ti-1)的权值各占0.5，是一种等值分配，实际过程中由于时间间隔的不对称等因素，相邻2个x(1)(ti)值不一定是等权的，存在一定的不合理性。在文献[12]引入的动态适应因子r(0≤r≤1)基础上，本文构造背景值为

z(1)(ti)=[(1-r)x(1)(ti)+rx(1)(ti-1)]Δti.

(6)

并且，以拟合值相对于实际值的平均相对误差绝对值达到最小为目标，提出一种权值搜索的背景值优化方法。

步骤如下：

Step 1:令r=0，计算模型的平均相对误差绝对值

Step 2:使r有一个较小的增加量，即r=r+Δr，计算此时的平均相对误差绝对值。

Step 3:利用计算机强大的计算功能重复Step 2，直至r=1。

Step 4:比较各个r对应的平均相对误差绝对值，最小的平均相对误差绝对值对应的r′值即为所求。代入式(5)得到优化后的背景值为

z(1)(ti)=[(1-r′)x(1)(ti)+r′x(1)(ti-1)]Δti.

(7)

1.2.3 初始条件优化

传统的非等间距GM(1,1)模型选取原始序列的第一个数据作为模型的初始值，已有学者[13]证明这种方式不能保证整个拟合序列的误差最小，反而还浪费了原始序列的第一点信息。现有的改进方法主要包括3种：①以原始序列x(0)(tm)(1≤m≤n)或者带有修正项的x(0)(tm)+c(1≤m≤n)作为初始条件[14]；②以原始序列每一个数据非等加权的和s1x(0)(t1)+s2x(0)(t2)+…+snx(0)(tn)作为初始值[15]； ③以原始序列和拟合序列的误差平方和或者相对误差平方和等衡量标准最小为约束条件[11]。

本文在背景值以平均相对误差绝对值最小为目标的基础上，仍以平均相对误差绝对值最小作为约束条件，优化模型，进一步减小拟合误差，提高模型精度。

由白化微分方程(3)可知其解为

(8)

离散化，

(9)

那么，优化模型建立的时间响应函数为

(10)

(11)

i=2,3,…,n.

(12)

1.2.4 新陈代谢预测

在非等间距GM(1,1)模型的实际应用中,新数据的加入带来新的扰动和不确定因素，系统会发生新的变化。距离时间原点越近的数据对预测的贡献越大，随着时间的推移，远离时间原点的老数据的信息意义不断降低。因此，模型在不断补充新数据的同时应该及时去掉老数据，不仅保证了最优的信息量，而且缩小了灰平面，提高预测精度。

本文对非等间距GM(1,1)模型进行等维处理，构造新陈代谢非等间距GM(1,1)模型对时刻tn+1至tn+h进行预测：

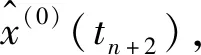
2 改进非等间距GM(1,1)-BP模型的构建

2.1 BP神经网络结构及算法

BP神经网络是由输入层、隐含层和输出层3个层次组成的一种前馈型神经网络。各层由若干个神经元构成，每一层上的神经元通过权重与相邻层上的神经元相连，每个神经元的输出值由输入值、阈值和作用函数决定。

假设输入向量X有n个元素，X=(x1,x2,…,xi,…xn)T，隐含层输出向量为Y=(y1,y2,…,yj,…ym)T，输出层输入向量为Z=(z1,z2,…,zk,…zl)T。从输入层到隐含层依次对应的权值向量集合为V=(v1,v2,…,vj,…vn)T，其中vj表示隐含层中第j个神经元所对应的权值向量；从隐含层到输出层依次对应的权值向量集合为W=(w1,w2,…,wk,…wl)T，其中wk表示输出层中第k个神经元所对应的权值向量。

对于隐含层有

(13)

对于输出层有

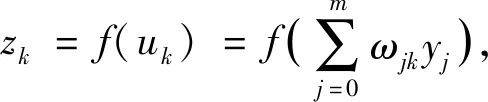
(14)

式(13),(14)中的f(x)为传输函数。

BP神经网络的学习算法包括2个方面：信号的正向传播和误差的反向传播。即根据最小二乘原理和梯度搜索技术，先将输入信息从输入层经隐含层正向传播至输出层，判断输出层是否得到期望的输出，如果不能，那么将输出值与期望值相比得到误差信号，误差信号经原来的路线反向传播的同时修正各层的连接权值和阈值，如此循环往复，直至实际输出值与期望值的均方误差最小为止[16]。

2.2 改进非等间距GM(1,1)-BP预测模型

灰色模型能够较好的预测数据变化的总体趋势,适用于发展态势明显的复杂问题，但是对于其他复杂形式的非线性函数或者突变情况拟合性能不是很理想，准确度普遍不高。然而,实际应用中数据变化往往是复杂的。考虑到BP神经网络可以以任意精度逼近非线性函数,将二者取长补短,构造基于改进非等间距GM(1,1)-BP模型是可行的。

模型构造步骤如下：

Step 1:构造差值序列。

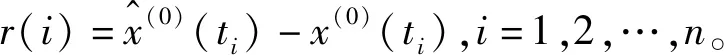
Step 2:采用滚动预测法建立差值序列的BP神经网络预测模型。

令阶数q=3，用r(i-3),r(i-2),r(i-1)(n≥i≥4)来预测r(i)的值。依次将r(i-3),r(i-2),r(i-1)(n≥i≥4)作为BP神经网络的输入，r(i)作为输出，对神经网络进行训练。

为方便计算，利用Matlab中的归一化函数mapminmax()分别对输入向量和输出向量进行归一化处理。

理论上，三层BP神经网络能以任意精度逼近任何非线性系统，因此，构建只含有一个隐含层的三层BP神经网络。显然输入层神经元数目为6，输出层为1，将隐含层神经元数目设置为10。采用Fletcher-Reeves变梯度算法作为训练算法，考虑到实际情况，设置学习速率为0.025，动量因子为0.9，精度为0.000 01，进行5 000次迭代。

Step 3:确定最终拟合值。

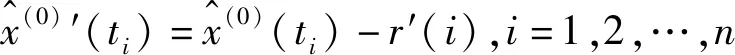
Step 4:获取最终预测值。

改进非等间距GM(1,1)-BP模型的流程图如图3所示。

3 预测实例及分析

以处于贮存状态的某型导弹为研究对象，选取从2009年初至2016年底，2个关键参数的30组不等间隔的测试数据，如表1所示，其余性能特征参数可采用相同的方法进行预测。将前24组测试数据用于训练学习，对后6组测试数据进行预测，并将预测结果同实际数据进行对比，以验证本文设计的非等间距GM(1,1)-BP模型的优越性。

利用文中提出的非等间距GM(1,1)优化建模方法建立测试参数c1的模型。可以得到发展系数和灰色作用量分别为a= 0.361 5，b=0.859 4。改进非等间距GM(1,1)模型为

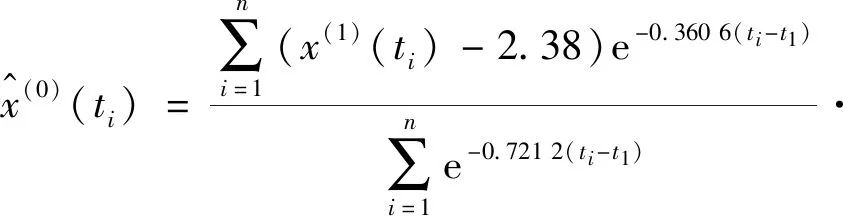
同理，测试参数c2的改进非等间距GM(1,1)模型为

表1 原始测试数据Table 1 Original test data

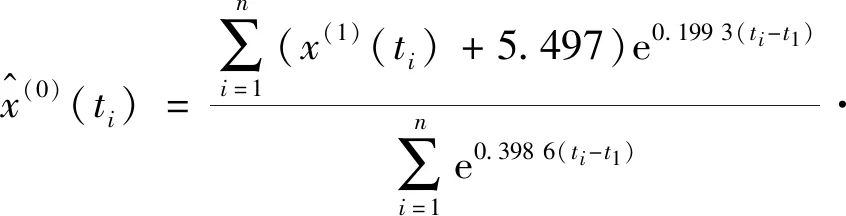
为了说明本文设计方法的有效性，将文献[10]、文献[11]、本文改进非等间距GM(1,1)模型和改进非等间距GM(1,1)-BP模型拟合结果进行比较分析，2个测试参数的拟合效果如图4,5所示，并分别以平均相对误差绝对值(MAPE)和残差平方和(RSE)作为拟合性能评价指标，如表2所示。

表2 测试参数拟合结果比较Table 2 Fitting result comparison of test parameters

由图4,5和表2可以看出，对于波动性较小的测试参数c2,本文建立的改进非等间距GM(1,1)模型能够较好地处理非等时间间隔数据，并且拟合效果明显优于文献[10]和文献[11]建立的传统模型。然而，由于灰色模型的局限性，对于波动性较大的测试参数c1而言，本文建立的改进非等间距GM(1,1)模型虽然相比于传统模型精度更高，但是总体效果不理想。通过对比表2中的数据可以明显看出，本文设计的改进非等间距GM(1,1)-BP模型拟合精度更高，且计算简便，易于实现。

通过上述拟合效果的比较，本文设计的非等间距GM(1,1)模型的优化效果显而易见。为了进一步检验本文设计方法应用于预测的效果，分别运用单一改进改进非等间距GM(1,1)模型和改进非等间距GM(1,1)-BP模型对后6组数据进行预测，2个测试参数的预测结果如图6,7和表3所示。

从图6,7和表3中可以看出，对于退化状态的预测，采用本文设计的方法相对于单一GM方法具有更高的预测精度。为了更直观地对预测结果进行比较分析，采用平均相对误差绝对值(MAPE)和预测有效度(Mp)作为预测评价指标，如表4所示。

从表4中可以看出，本文设计的改进非等间距GM(1,1)-BP模型的平均相对误差绝对值更低，预测有效度更高，从而验证了本文设计方法的合理性和优越性，具有较大的实际应用价值。

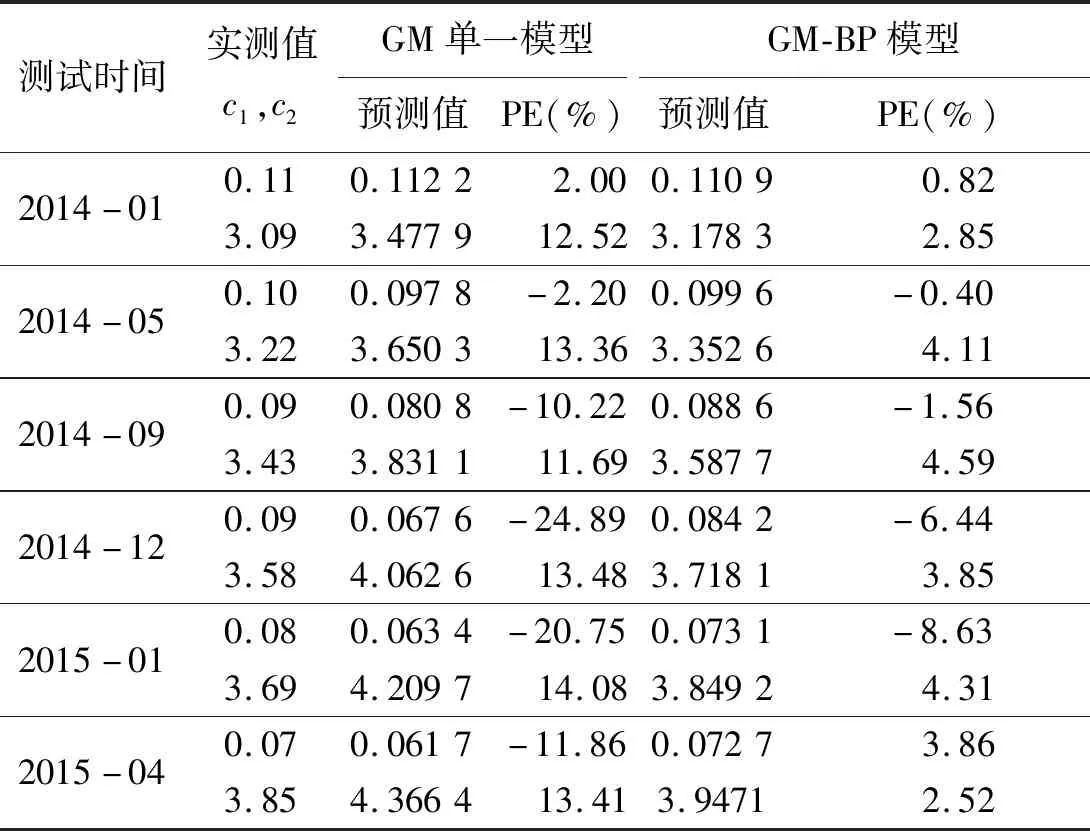
表3 测试参数预测结果比较Table 3 Prediction result comparison of test parameters

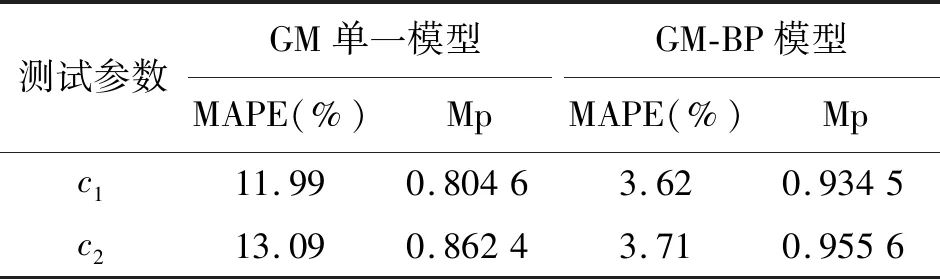
表4 测试参数预测结果对比Table 4 Prediction result comparison of test parameters

4 结束语

本文结合灰色模型预测方法和神经网络预测方法的优势，提出了一种基于改进非等间距GM(1,1)-BP模型的导弹退化状态预测方法。该方法通过优化灰色模型的背景值和初始条件，结合新陈代谢思想建立改进的灰色模型，增强了数据的规律性，再通过BP神经网络强大的非线性拟合能力提高了预测精度，同时克服了常用预测模型无法针对非等时间间隔数据建模的问题。实例结果证明了本文设计的方法具有更高的预测精度，且计算简便，可为状态评估及维修决策提供可靠依据，具有不错的工程应用前景。