基于RBF神经网络参数自整定的AUV深度控制

2019-07-16 06:16杜度

水下无人系统学报 2019年3期

杜度

(海军研究院,北京,100161)

0 引言

自主无人航行器(autonomous undersea vehicle,AUV)作为一种海洋探索的重要工具,在现代和未来的海洋资源勘探中有着不可替代的地位,因此受到国内外重视[1-3]。在深海探测中保持固定深度航行的能力是确保AUV探测水下资源的基础,因此研究 AUV的深度控制就显得尤为重要。

AUV深度控制方法有反步法、模糊控制法和自适应滑模控制法等[4-8]。Khodayari等[9]设计了一种新型的自适应模糊PID控制器,通过组合自适应方法和双比例-积分-微分(proportional-integral-derivative PID)控制器改善PID参数和AUV建模不确定性。Wei等[10]基于非线性观测器设计了针对深度控制的反步法控制器,使其对外界干扰具有较强的鲁棒性。贾鹤鸣等[11]利用反步法设计了一种滑模控制器,但未考虑外界环境存在干扰的问题。郭小溪等[12]给出参数最优指标,利用遗传算法实现了PID参数的自整定。王宏建等[13]提出具有PID增益调节的AUV深度控制方法,基于反馈增益的反步法设计控制器,避免了采用传统反步法导致控制器中存在虚拟控制量的高阶导数问题,但在控制器设计中未考虑外界干扰问题。Li等[14]提出了一种基于神经网络的自适应控制方法,但由于反步法设计中存在虚拟控制量的导数高阶过高,导致了控制器的计算较为复杂。汪伟等[15]基于滑模变结构设计了一种 AUV深度控制器,利用模糊神经网络对滑模控制律的控制增益进行在线调整,但是收敛速度较慢,且控制任务单一,不能快速跟踪复杂期望轨迹。梅新华等[16]利用反向传播(back propagation,BP)神经算法自主优化艏艉舵进行定深航行,但同样存在收敛速度较慢的问题。

为解决控制器参数设定过程中存在反复调整的问题以及可能存在参数非最优的情况,文中利用径向基函数(radial basis function,RBF)神经网络可以快速地逼近任意非线性函数的性质,设计了神经网络的识别函数,使神经网络输出能够逼近期望轨迹。利用梯度下降法对PID参数进行自整定,有效地减少了调整参数的时间同时保证控制器的控制效果最优及其参数值的最优性,使AUV可以在较短时间内到达指定深度。

文中首先对六自由度的 AUV运动学和动力学模型进行简化,得出深度控制模型;然后简述了RBF神经网络的基本原理,并给出其逼近网络的具体公式;为方便进行数字仿真,设计出离散条件下的PID控制器和RBF网络自整定PID参数的性能目标函数和迭代公式;最后通过MATLAB仿真试验得出自整定 PID参数以及AUV深度控制的实际曲线和误差值。试验证明RBF神经网络可以在较短时间内确定最优参数,并保证AUV达到指定深度。

1 AUV深度控制模型

AUV的空间运动具有六自由度,通常可以在地球固定坐标和船体移动坐标下描述其运动状态,AUV在2个坐标系中的示意图如图1所示。

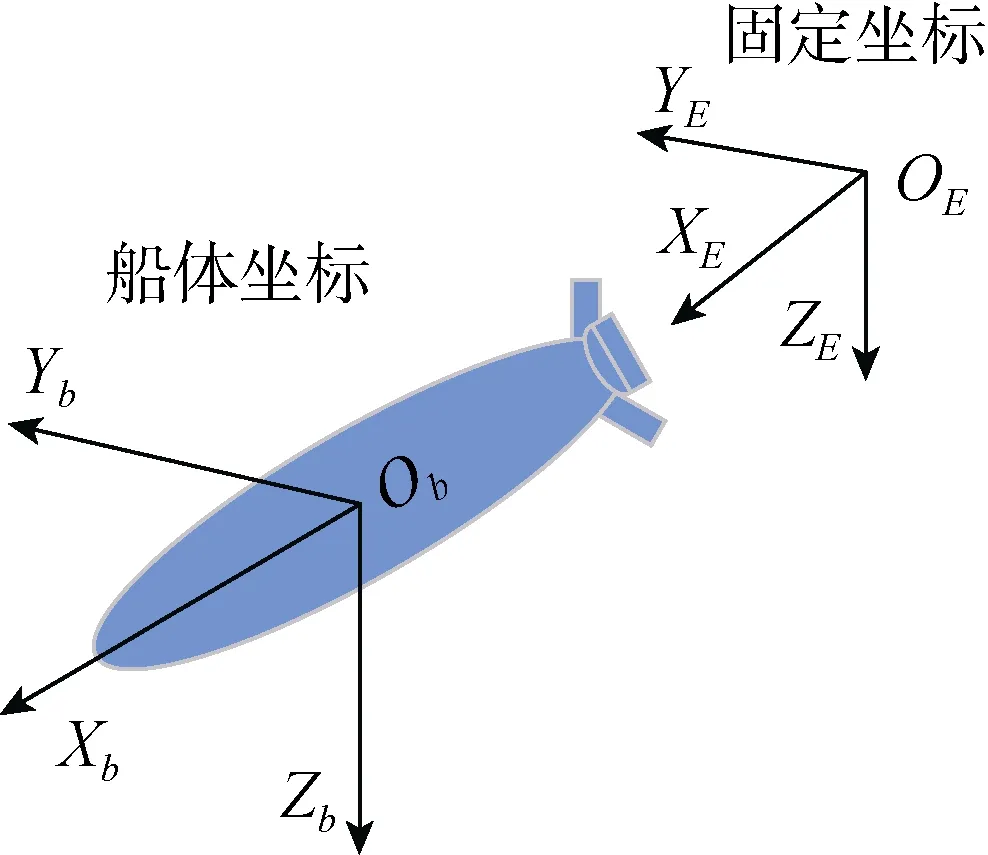
图1 自主水下航行器坐标系示意图Fig.1 Coordinate systems of autonomous undersea vehicle(AUV)

在深度控制中,从实际考虑出发,只考虑 AUV在垂平面的运动状态,并忽略垂向速度、横向速度以及横摇和首摇运动。因此可以得到简化后的AUV深度控制的运动学与动力学模型[17]。

运动学模型

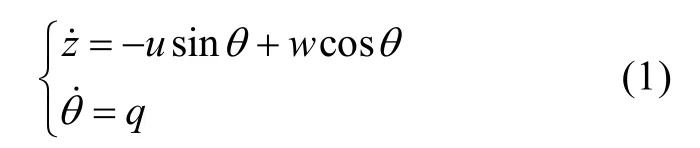
动力学模型

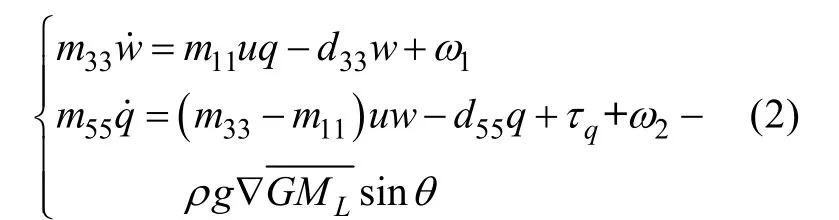
式中:z,θ,u,w,q是系统状态量,分别表示 AUV的垂荡量、纵摇量、纵荡速度、垂荡速度和纵摇速度;其中m为 AUV 质量,和为附加质量,Iy为绕y轴的转动惯量,Zw和Mq为一次水动力系数,为二次水动力系数;ρ,g,分别代表水密度、重力加速度、AUV的排水体积和纵向稳心高;ω1,ω2为海浪干扰;τq为控制输入。

2 RBF神经网络原理

2.1 基本原理

RBF神经网络早在1988年由Broomhead等[18]提出,是基于生物学理论的一种神经元网络结构,模拟了人类大脑皮层区域中局部调节和交叠感受野(receptive field)的人脑反应机制。RBF神经网络是能在紧凑集和任意精度下逼近任意非线性函数的向前网络,相比于早期 BP网络具有很好的泛化能力,因此广泛应用在模式识别和非线性控制领域中。RBF的网络结构为3层向前网络(见图 2)。

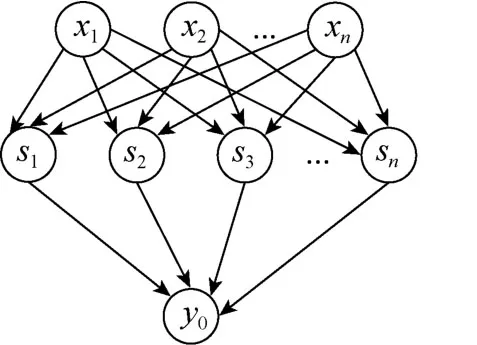
图2 径向基函数神经网络结构图Fig.2 Structure of radial basis function(RBF)neural network

RBF神经网络结构模型的第 1层为输入层,其输入向量表示为其中,n为输入量个数。第2层为隐含层,隐含层为神经元激活函数,由径向基函数构成,其径向基向量表示为其中,m为节点数,sj,j∈m为高斯基函数

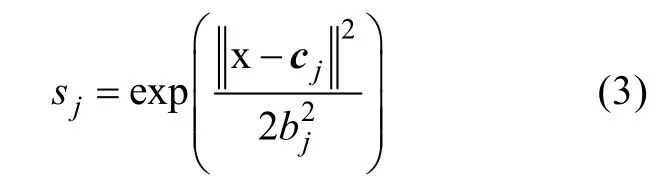
式中:bj为高斯基函数的宽度;cj为第j个节点的中心矢量,第3层为输出层,输出为加权函数,表示为

2.2 RBF神经网络逼近

从上节可知,RBF 神经网络是一种具有3层结构的静态前馈型网络。因为隐含层中的转移函数是高斯函数,所以与BP神经网络相比RBF神经网络具有更多的神经元。并且 RBF 神经网络的另一个优势就是可以根据具体情况在训练阶段调整隐含层单元数,并且其输出值也和初始权值设置没有关联,因此RBF神经网络可以很好地避免复杂系统中可能存在的初始值参数设置问题。

从训练速度上看,RBF 神经网络的收敛速度要好于 BP 神经网络,这是因为 RBF 神经网络结构的层数较少,BP 神经网络的结构较前者更为复杂。其次,RBF 神经网络中的输入和高斯函数中心点的距离决定了隐含层的权值,特定的任务中,可以有效利用其网络结构,根据训练样本的布局和隐层单元的宽度,优化和选择训练权值。因此,RBF神经网络的3层网络结构使其更广泛应用于非线性函数逼近。

网络逼近性能指标函数为

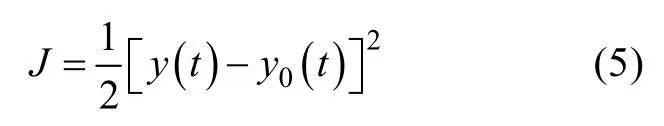
为使 RBF进行有效学习,利用梯度下降法迭代输出权值、节点中心值和节点基宽参数,分别为

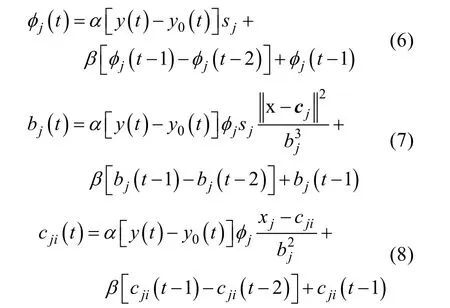
式中:α为学习效率;β为动量因子。

3 RBF神经网络PID参数自整定

为利用 RBF神经网络进行参数自整定,首先要定义整定目标,即选定整定函数。AUV深度控制的目标是使其跟踪期望轨迹,使深度跟踪误差在有限时间内收敛。文中采用的控制系统结构图如图3所示。

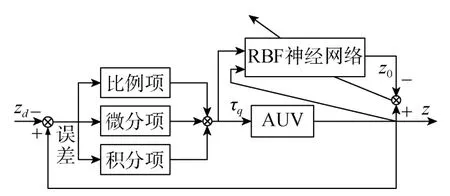
图3 控制系统结构图Fig.3 Structure of control system

图3中右端输出为实际深度值;左端输入为实际深度与期望深度的差值,将差值代入比例项kP,积分项kI,微分项kD表达式中,并输入至RBF神经网络;同时将PID控制器τq代入AUV模型中;之后将实际输出深度,辨识网络的输出与实际输出深度的差值代入 RBF神经网络进行整合。

令AUV进行深度控制的期望路径设为zd（t）,因此根据其实际深度z（t）构成路径误差

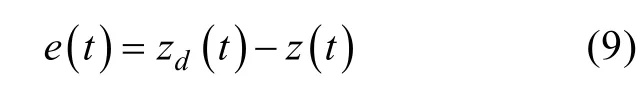
为保证 AUV按期望路径航行,要使误差为零,选取神经网络整定目标

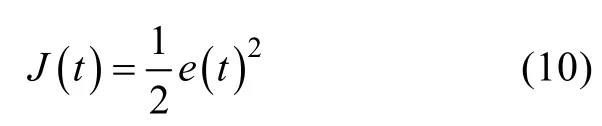
采取离散式PID控制器

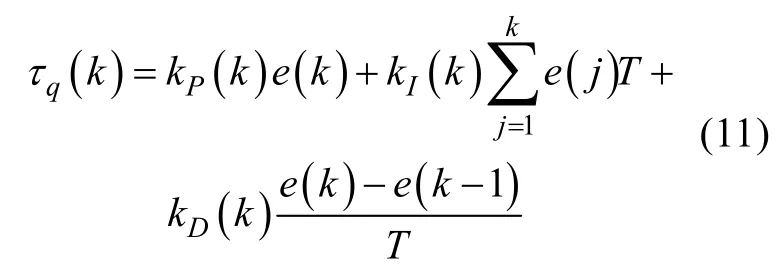
式中,t=kT,kP,kI,kD采用梯度下降方法,表达式为

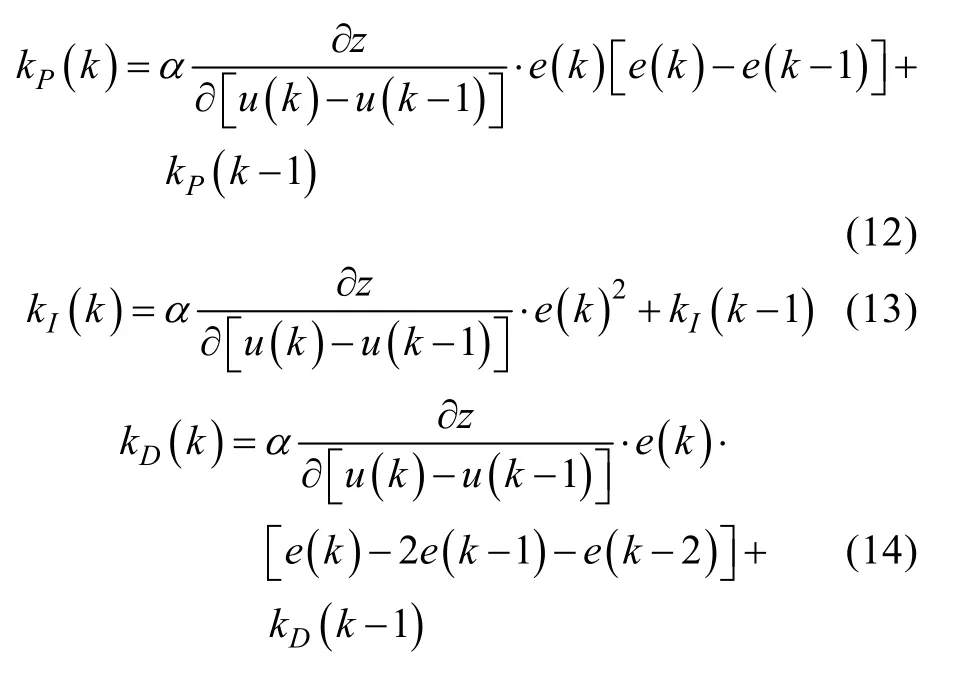
4 数值仿真

利用 MATLAB进行试验仿真,验证文中所设计控制器的有效性。设AUV航行速度为2 m/s,深度初值z′=0,期望深度zd=10。首先任意给出PID参数初值传统PID控制参数对控制输入进行限制,即采样周期T=0.01s。海浪干扰10·si n(0.01t)。学习效率为α=0.5,动量因子为β=0.05;输入权、节点中心和节点基宽的初值都设为零。

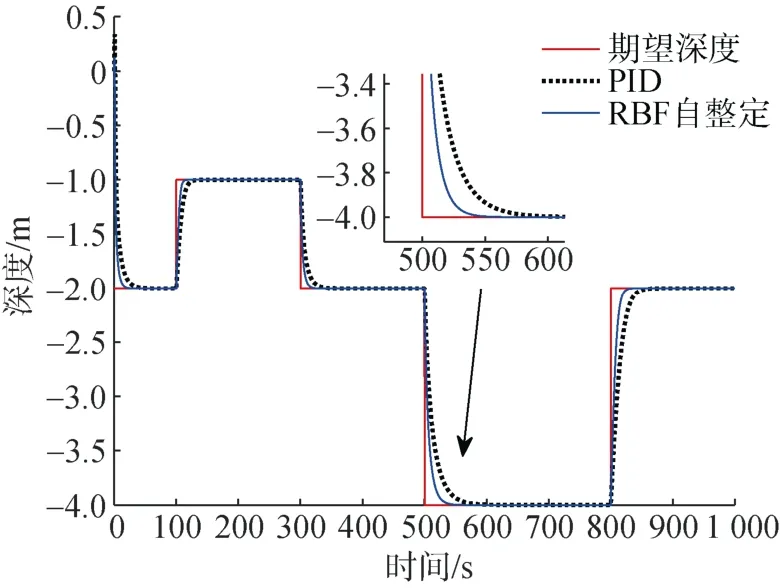
图4 AUV深度控制曲线Fig.4 Curves of AUV depth control

通过图4可以看出AUV实际的深度控制能够较快达到指定深度,与传统控制方法相比可以在较短时间内跟踪误差。通过图5可以看出,AUV的深度控制的误差很快趋于零,与传统PID相比误差相对较小,从图 4局部放大图可以看出,在RBF自整定PID控制下可以在更短时间内收敛。控制输入曲线如图6所示。图7可以看出PID参数只需设定初始值,就可以在很短时间内完成自整定,保证其控制效果最优及其参数值的最优性,使AUV在较短时间能到达指定深度。

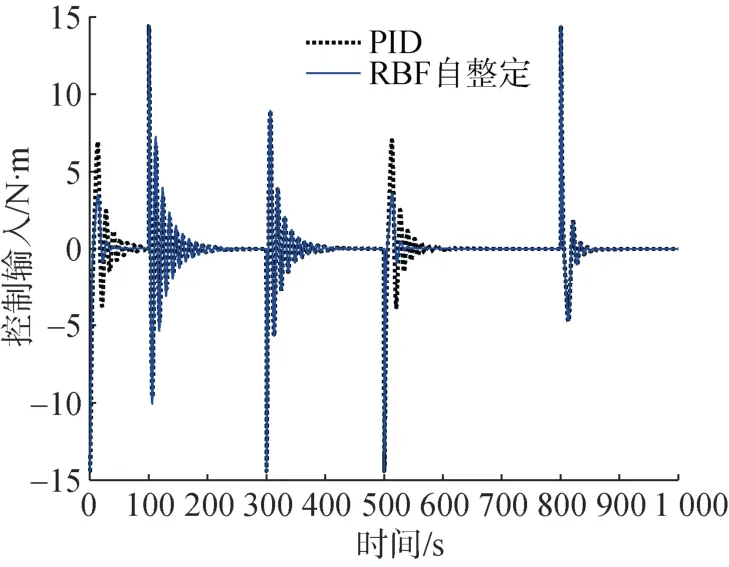
图6 AUV控制输入曲线Fig.6 Curves of AUV control input

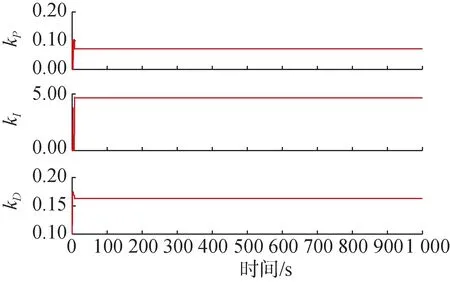
图7 PID参数自整定曲线Fig.7 Curves of PID parameter self-tuning

5 结束语

文中针对传统PID控制器参数整定问题,提出了一种基于RBF神经网络的参数自整定 PID深度控制器。首先根据 AUV运动规律给出其垂平面的运动学和动力学方程;其次设计了 AUV深度控制系统的控制结构,给出了RBF网络整定目标函数和PID控制器中各个参数项的离散形式;最后对AUV深度控制进行仿真研究,与传统PID控制器进行对比,结果表明文中提出的基于RBF神经网络参数自整定控制方法优于传统PID控制方法,并且验证了该方法对PID参数自整定的有效性。

在实际的 AUV执行机构中,控制输入可能会存在时滞问题,未来将考虑在控制输入时滞情况下的AUV深度控制,以提高控制器的适用性。