特征法视觉SLAM逆深度滤波的三维重建
张 一,姜 挺,江刚武,余岸竹,于 英
信息工程大学地理空间信息学院,河南 郑州 450001
视觉即时定位与地图构建(visual simultaneous localization and mapping,VSLAM)技术,以视频序列影像为输入,能够在恢复相机运动轨迹的同时,实时重建未知场景的三维结构,可用于无人机、车辆、机器人等平台的智能环境感知、自动驾驶与导航[1],也可用于应急测绘、灾害与突发事件监测、虚拟与增强现实等场景,具有广阔的应用前景与市场潜力[2-3]。
目前视觉SLAM算法主要采用基于关键帧优化的特征法[4-6]进行实现,其基本流程是:首先从每幅影像中提取出具有可重复性与显著区分性的点、线特征;使用不变性描述符在后续帧中对特征进行匹配,利用多视图几何原理恢复相机位姿与结构,然后通过光束法平差[7]进行联合优化。
在诸多特征法SLAM中最具代表性的是ORB-SLAM[8-9],它采用统一的ORB[10](oriented FAST and rotated BRIEF)特征进行计算,在室内外环境中均能稳健、实时运行,可在大视角差异下完成重定位与闭环检测,并且由像点匹配累积的共视[6]信息可用于构建强壮的平差与图优化[11]网络,有利于得到全局最优解。ORB-SLAM的主要缺陷在于,地图点通过两关键帧三角化直接得到,对于短基线视频影像,其深度不确定性较大,为避免粗差必须采取严格的筛选策略,导致所构点云地图十分稀疏。此外,ORB-SLAM的非关键帧在追踪完后即被抛弃,其对地图点深度信息无贡献,造成了资源浪费。
从应用层面看,稀疏点云仅可用于传感器的自身定位,而较高级的视觉导航、避障、虚拟增强现实、模型重建、语义识别等应用,都需要更加稠密的地图表达。为此,直接法相关技术获得了更多关注,它根据像素亮度差异直接构建优化问题求解相机位姿,并采用一种基于概率分布的深度滤波器模型[12-14],利用多帧影像更新地图点深度信息。早期的直接法多根据稠密深度图进行计算,以最大化利用影像信息并增加稳健性[15-17],这类算法一般需要GPU加速来满足计算要求。文献[14,18]使用具有显著梯度的像素,在CPU上完成了较稠密的实时重建;文献[13,19]提出了仅需少量像素的稀疏直接法,使算法具有更强的适用性。
直接法不必进行特征提取与匹配,因而具备了更高的计算效率,但它易受相机曝光、环境光源等因素影响,当场景亮度变化剧烈时可能导致求解失败,稳健性不足[2]。另外,直接法优化基于像素本身进行操作,该过程需要完整的影像数据,对于大规模场景来说,由于设备存储空间有限,直接法难以进行全局质量控制。为此文献[20]将概率分布构图方法应用于ORB-SLAM中,使得其在保留特征法优点的同时,能够重建出精确的稠密场景结构。但由于其构图模块独立于ORB-SLAM系统并具有若干关键帧的延迟,严格意义上并不属于在线处理,并且构图结果无法用于后续帧的位姿追踪,作用有限。
在总结前文算法的基础上,本文提出一种特征法视觉SLAM逆深度滤波的三维重建方法,无须GPU加速即可实时、增量式地重建出较为稠密的点云地图。在前端中,设计了一种基于运动模型的参考关键帧追踪流程,能够有效利用视频影像先验约束获取精确的相对位姿关系;建模并分析了深度估计误差,采用一种基于概率分布的逆深度滤波器构图方法,可得到更加稠密的地图点。在后端中,提出一种基于特征法与直接法混合的优化框架以及基于平差约束的点位筛选策略,可以准确、高效地恢复相机位姿与场景结构。
1 总体流程与关键技术
1.1 总体流程
本文核心思路是:地图点不再由两帧三角化直接得到,而是先构造为种子点,经多帧信息融合直至深度收敛后再插入地图。为此设计总体流程如图1所示,系统以ORB-SLAM为基础框架,仍采用前后端结合的三线程结构,主要改动集中于追踪与局部构图线程,以粗体表示。
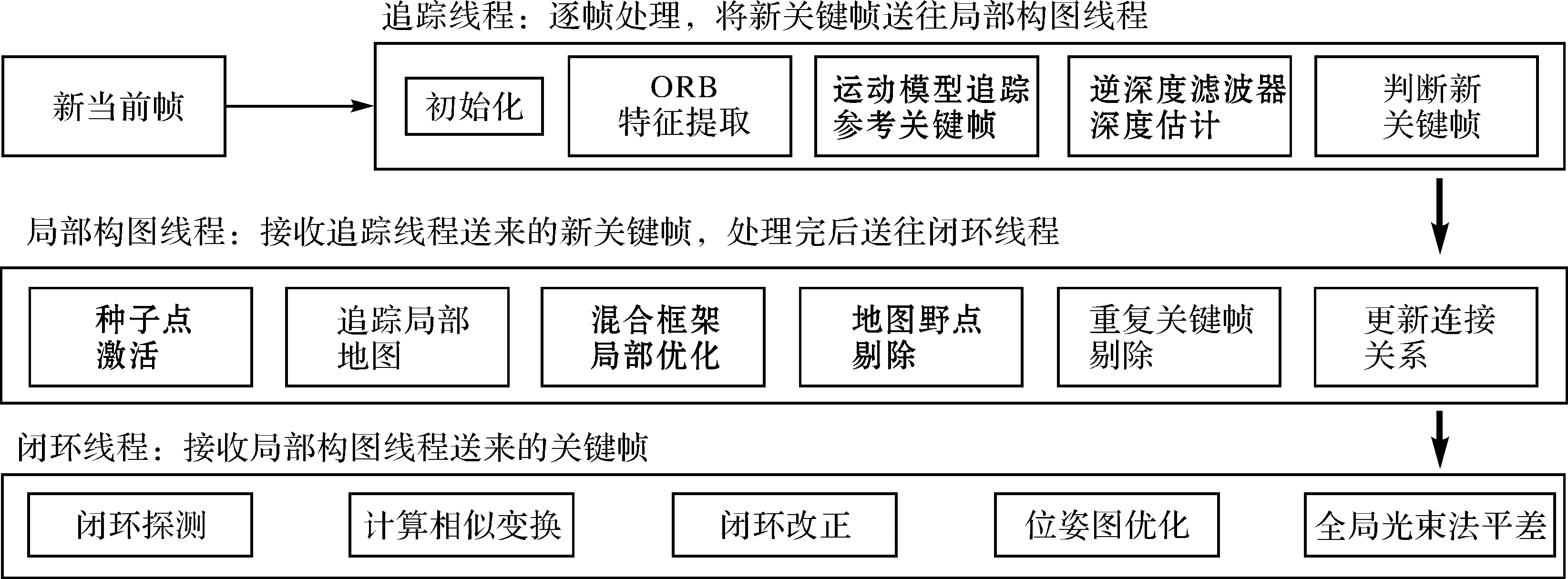
图1 本文方法总体流程Fig.1 Flowchart of the proposed algorithm
对于输入的每一帧视频序列影像,首先在前端追踪线程中提取ORB特征,利用运动模型提供的帧间先验约束,将参考关键帧的地图点投影至当前帧,进行特征匹配与位姿估计;然后在逆深度滤波器中对参考关键帧的种子点进行极线匹配并更新其深度;最后判断该当前帧是否应作为新关键帧插入局部构图线程。
后端局部构图线程收到新关键帧后,首先将原参考关键帧中所有深度收敛的种子点激活为新的地图点,并与邻近关键帧的其他局部地图点一起投影至新关键帧以建立更多匹配;随后根据各地图点的观测情况,采用一种基于特征法与直接法的混合框架优化方法,联合求解局部相机位姿与场景三维结构;在剔除掉地图野点与重复关键帧后,将新关键帧作为后续影像的追踪参考帧,其未匹配的特征点构造为新的种子点;最后,将新关键帧送入闭环线程以实现最优全局一致性。
1.2 运动模型追踪参考关键帧
准确的极线几何关系是本文逆深度滤波器顺利更新种子点深度的前提,因此前端系统需提供当前帧Ic关于参考关键帧Ir的精确相对位姿Tcr∈SE(3)。然而ORB-SLAM采用逐帧追踪的方式,当前帧并不直接与参考帧进行匹配,Tcr只能通过间接方式求出,由于存在误差累积等因素,该方法用于逆深度滤波器的效果较差。为此本文设计了一种新的追踪方式,可直接计算当前帧关于参考关键帧的相对位姿Tcr,基本流程如图2所示。
由于视频影像通常具有较高帧率,相机运动一般比较平稳,具备丰富的先验信息,能够为追踪系统提供良好的初值。常速运动模型假设短时间内相机帧间相对位姿保持不变,即
Tc,c-1=Tc-1,c-2=Tv
(1)
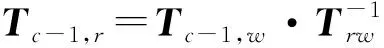
(2)
1.3 逆深度滤波器
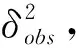
(3)
由式(3)可知,观测融合后深度估计的方差会减小,当其小于某一阈值并趋于稳定时,就认为该点的深度值收敛。本文采用文献[13]提出的方法对深度估计误差进行建模。如图3所示,设左影像Ir为参考关键帧,右影像Ic为已追踪的当前帧,O1、O2分别为两帧相机光心位置,基线长b,P为同名像点p1p2经三角化得到的空间点,其在左影像中的深度值为dp,P、O1、O23点的夹角分别记为α、β、γ,l2为p1在当前帧Ic中对应的极线。
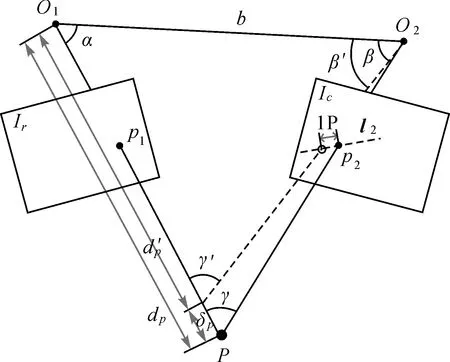
图3 深度估计误差模型Fig.3 Error model of depth estimation
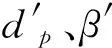
(4)
理论上,深度滤波器只需不断将当前帧得到的深度估值与方差作为新的观测,与已有数据进行融合即可。然而实际过程中,由于位姿估计不够准确、匹配错误等诸多原因,观测值可能存在粗差,将会对融合结果产生较大影响,因此必须对该过程进行优化。
首先,文献[21]发现逆深度(即深度值的倒数)的统计直方图更接近正态分布,因此在计算出P点深度值dp后,将其换算为逆深度ρp=1/dp,相应的误差计算公式为
(5)
其次,考虑到单像素的亮度与梯度没有明显的可区分性,易受噪声影响,本文采用文献[19]提出的8像素-图像块模型,用各像素的梯度均值作为中心像素的梯度,并按照距离平方和(sum of squared distance,SSD)测度进行极线搜索匹配,能够保证较高的准确度并兼顾效率,如图4所示,其中p1为待匹配点,pmin与pmax分别是按照最大与最小逆深度值(ρp±3δρ)计算的空间点P投影到当前帧的像点,两点连线即为极线段向量l2。
此外,匹配点像素梯度与极线的夹角也对深度滤波器有重要影响,随着像素梯度与极线段夹角的增加,极线匹配的不确定性也会增加[22]。由于视频影像帧率较高,帧间相对旋转较小,可将参考帧Ir上p1点的图像块平均梯度gp作为当前帧Ic匹配点p2梯度的近似,于是由像素梯度与极线夹角造成的误差可被定义为
(6)
式中,n2表示极线段l2的法向量。由式(6)可知,当l2与gp平行时,Ep取得最小值,反之当l2与gp垂直时Ep取得最大值。在实际计算过程中,若Ep小于某一阈值,并且极线搜索的最优匹配SSD小于次优匹配的一半以上,就认为该点的深度观测有效,可以对其进行高斯融合。
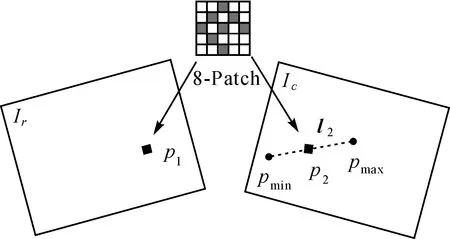
图4 图像块模型与极线搜索Fig.4 Patch model and epipolar line search
1.4 后端混合局部优化框架
后端优化是维持SLAM系统一致性的关键,在ORB-SLAM中该问题可以通过局部光束法平差解决,但由于本文方法地图点是通过深度滤波算法构造的,在初始化时仅能够被当前关键帧观测,无法按照重投影误差最小化原理进行优化。为此本文提出一种基于特征法与直接法的后端混合局部优化框架。
首先,对于观测数大于等于3的地图点,采用光束法平差联合求解相机位姿与地图点位置。然后,对每个观测数小于3的地图点,将其投影到其他关键帧,按照直接法辐射误差最小化原理,对该点深度值进行优化。该过程可以用因子图的形式表达,如图5所示,MP1与MP2表示待优化的地图点,HostKF表示构造这两个地图点的主帧,LocalKF表示与主帧存在共视连接的局部关键帧,Ob表示地图点投影到目标关键帧形成了一次观测(观测的主帧与目标帧分别用红线和蓝线表示)。
假设图像块模型中的各像素具有相同的逆深度值,以MP1为例,其深度优化目标函数为
(7)
以及对应的误差项
(8)
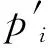
采用该优化框架的好处非常明显:首先,观测数较多的地图点往往具有较好的稳健性,平差系统能够减少野点风险, 准确恢复相机位姿与场景结构[23],如图6(a);其次,这类地图点数量稀疏,平差负担小;而经直接法优化的地图点,如图6(b),尽管比较稠密,但未知数仅有一个,且各点解算过程相互独立,可采用并行策略进行加速,从而提高优化效率。
由于误匹配等原因,系统在运行过程中不可避免会出现地图野点,需予以剔除。对于新构建的地图点,ORB-SLAM根据其在后续若干关键帧中的匹配情况进行筛选,该策略无法用于本文直接法优化的地图点(匹配数不足,总是会被剔除)。为此,提出一种基于平差约束的筛选策略,每次后端优化完成后,检查所有新构建的地图点,如果满足以下任一条件,就会被标记为野点并剔除。
(1) 经局部光束法平差优化后,重投影误差未通过χ2测试被标记为野点的;
(2) 经直接法优化后,能量函数超过阈值被标记为野点的;
此外,如果一个地图点被标记为野点,并且其主帧是最新的两个关键帧之一,就重新将该点构造为种子点进行深度滤波。本文策略能够在排除野点的同时,有效增加点云密度。
2 试验与分析
2.1 试验数据与评价方法
利用3组数据进行验证,如图7所示,第1组数据选自开源TUM RGB-D数据集[24],采用移动机器人搭载Kinect相机拍摄,拍摄环境为室内,本文仅利用其中的RGB数据,数据集提供了完整的相机参数以及由高精度IMU获取的位姿数据作为评价真值。
第2、3组数据由大疆精灵4无人机相机获取,其中第2组采用手持方式,拍摄对象为室内机房,第3组采用航拍方式,拍摄对象为室外建筑,相机预先经过标定并对原始影像进行了几何畸变校正,3组数据均包含完整闭合回路,基本信息见表1。依据本文方法,在Ubuntu16.04系统下开发了验证算法ZY-SLAM,所用PC配置为:Inter Core i7 2.6 GHz、DDR3 16 GB,未采用GPU加速。

表1 试验数据基本信息
由于本文方法基于ORB-SLAM框架实现,故以其作为主要比较对象,考虑到ORB-SLAM只能得到稀疏点云,而较为稠密的三维结构表达又是直接法视觉里程计(visual odometry,VO)的研究热点,因此采用当前具有代表性的DSO[19](后文称DSO-VO,区别于SLAM)共同比较,按如下3种方法分析本文方法性能:
(1) 通过比较系统处理影像的整体及关键环节运行时间,验证算法的计算效率;
(2) 通过计算轨迹误差,分析算法的相机位姿估计精度;
(3) 通过目视检查,评价算法的重建效果。
2.2 计算效率分析
表2显示了采用本文方法与ORB-SLAM对TUM_Desk数据进行处理的系统运行时间对比(由于DSO计算流程存在较大差异,这里未进行对比)。本文方法的总体效率优于ORB-SLAM,每帧平均处理时间约36 ms,帧率28 fps,基本满足实时要求。
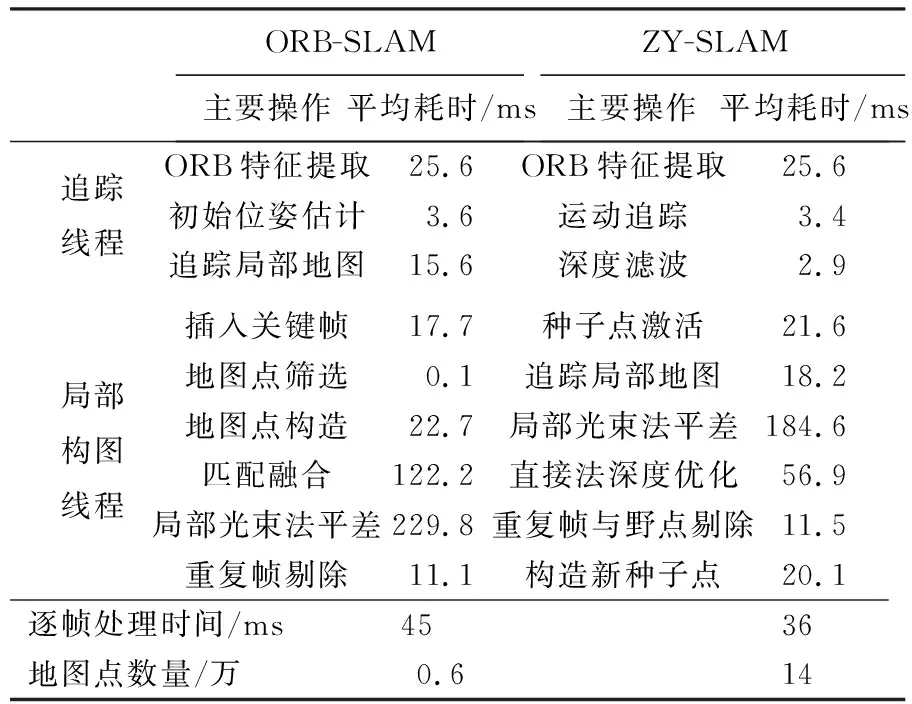
表2 系统总体运行时间对比
考虑到本文方法地图点数量超过ORB-SLAM的20倍,综合效率提升非常显著,这主要得益于:①追踪线程中,本文方法采用追踪参考关键帧的方式进行位姿估计,不再逐帧追踪局部地图,节省了大量资源;②局部构图线程中,影响计算效率的主要是局部平差。本文算法采用的混合优化框架,能够在准确恢复相机位姿与场景结构的同时,有效降低平差规模,不仅可以减少局部平差优化被中断的次数,也可以更好地平衡追踪与局部构图这两个并行线程的关系,使系统更加流畅。
上述试验结果也证明由深度滤波构造地图点的方式更适合SLAM系统。从效率角度看,深度滤波利用若干相邻帧影像更新深度,由于基线较短,极线搜索范围小,匹配成功率高,计算负担低,系统运行更平滑,更符合增量式重建的特点,而ORB-SLAM为保证深度估计的可靠性,只在关键帧上进行极线匹配,虽然基线较长,但搜索范围大,耗时较长,同时由于影像函数的高度非凸性,可能存在若干接近最优匹配的“次优匹配”结果。从实用性角度看,深度滤波过程中,倘若某次观测出现粗差,只需跳过该次观测,系统仍可利用后续观测准确估计深度,而在ORB-SLAM中,地图点由两关键帧直接计算,为避免粗差就需采用多种组合策略进行约束,实际能够通过测试的点对非常少,这也是ORB-SLAM只能输出稀疏点云的主要原因。
2.3 相机轨迹误差分析
位姿估计是SLAM系统的核心,其精度受地图点精度的影响,并且反过来也直接影响所构建的地图点。由于本文方法属于单目视觉SLAM,存在尺度不确定性,且位姿估值可以被定义在任何坐标系下,无法直接与真值进行比较,本文采用轨迹误差来衡量算法的位姿估计精度。其思路是,先利用最小二乘得到位姿估值序列与真值序列的相似变换S∈Sim(3),将估值换算至同尺度真值坐标系下再计算各帧的相对变换。轨迹误差一般只计算平移分量,这是因为它更加直观,并且也潜在地受到角度差异的影响[24]。此外,对于第2、3组无人机影像数据,由于缺乏高精度POS实测的位姿真值,本文利用ContextCapture[25]软件对影像数据进行三维建模并将其空三结果作为评价真值使用。结果如表3所示。

表3 不同方法位姿估计轨迹误差比较
本文方法的位姿估计精度较ORB-SLAM有所提升,分析原因如下:①由深度滤波获取的地图点融合了多帧观测结果,相比于直接通过两帧三角化得到地图点的方式,信息利用更加充分,三维位置更加准确,对位姿估计产生积极影响;②由于地图点数量较多,后端光束法平差可以仅采用观测数多的点估计相机位姿,有助于减小野点对最小二乘系统的影响;③特征点匹配率更高,一定程度上增加了多余观测,能够提高位姿估计的稳健性。图8显示了不同数据集的关键帧特征点匹配率,本文方法在大部分情况下均高于ORB-SLAM。
此外,本文方法与ORB-SLAM的位姿估计精度明显高于DSO-VO,这是因为前两种方法均可利用闭合回路约束减少累积误差影响,而DSO-VO不具备此功能,轨迹误差的累积效果在图9中尤为明显。
2.4 三维重建效果
在准确恢复相机位姿的前提下,本文方法无须GPU加速即可重建出较为稠密的场景三维结构,如图10所示,从而使虚拟现实、机器感知、语义识别等更高级别的地图应用成为可能。这主要得益于,逆深度滤波器可以构造大量地图点,且一个地图点无论观测情况如何,都可以通过后端混合框架进行优化。观察可发现,本文方法点云地图中包含许多非角点的物体轮廓、边缘信息,这是ORB-SLAM无法实现的。
与此同时, 本文方法可以准确地识别并进行闭环改正[26],得到全局一致的位姿与地图信息,而DSO尽管也具备优异的局部重建性能,但由于其采用的直接法平差需利用完整影像数据,在资源受限的情况下难以进行全局质量控制,导致所构建地图出现重影,如图11、图12所示,影响重建效果与准确性。
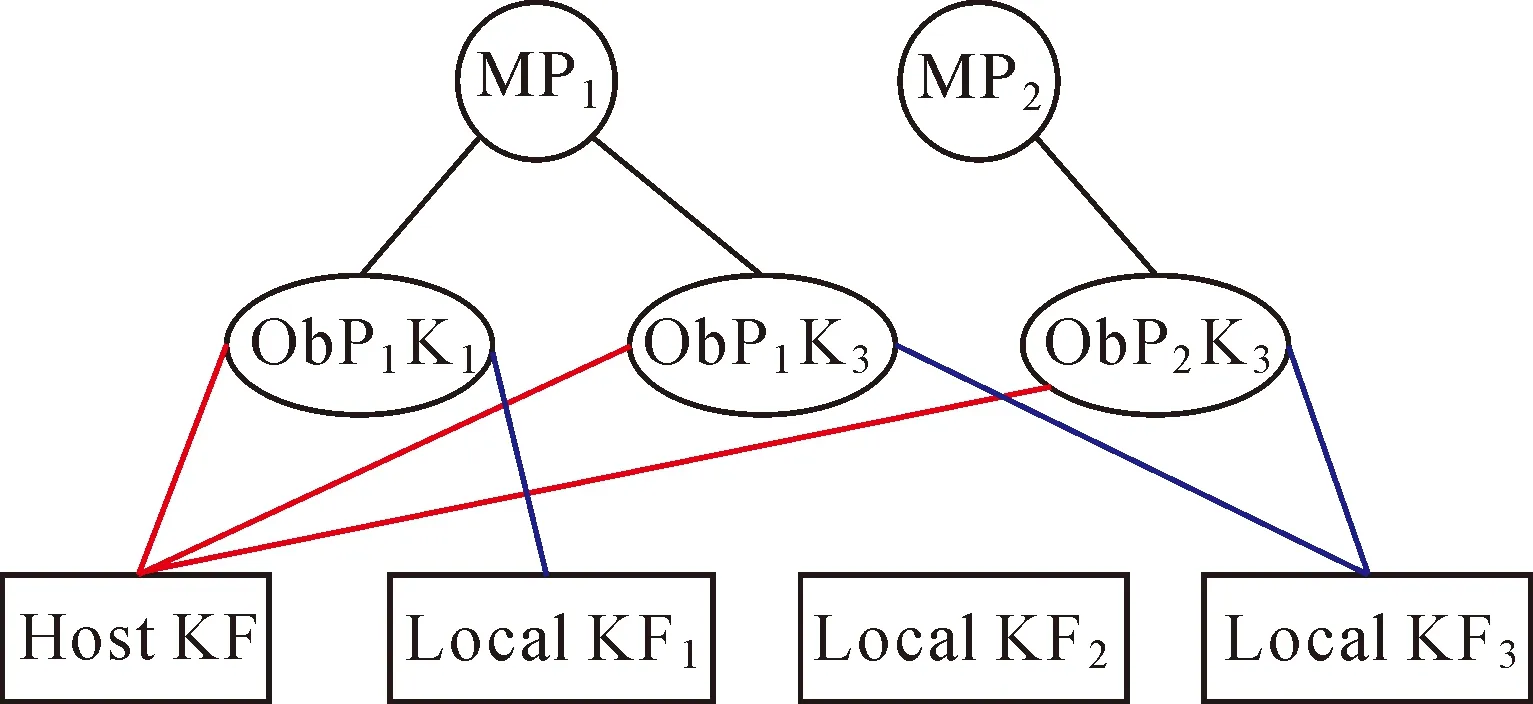
图5 直接法深度优化因子图Fig.5 Factor graph of direct depth optimization

图6 不同类型地图点Fig.6 Different types of map points

图7 试验数据Fig.7 Data examples
3 结 论
本文提出一种特征法视觉SLAM逆深度滤波的三维重建方法,关键在于地图点深度不再由两帧三角化直接获取,而是由基于概率分布的逆深度滤波器累计更新得出。除了计算效率与位姿估计精度方面的优势,更重要的是,该方法能够在保证全局一致性的前提下,显著提升重建点云密度,准确、高效地恢复场景结构细节,为视觉SLAM在机器人智能感知、自动驾驶、应急测绘等领域的进一步应用提供了新思路。未来将针对点云的去噪策略与平滑约束、重建精度定量评价等问题继续开展研究,同时也将采用更多类型的影像数据进行更加广泛的测试。
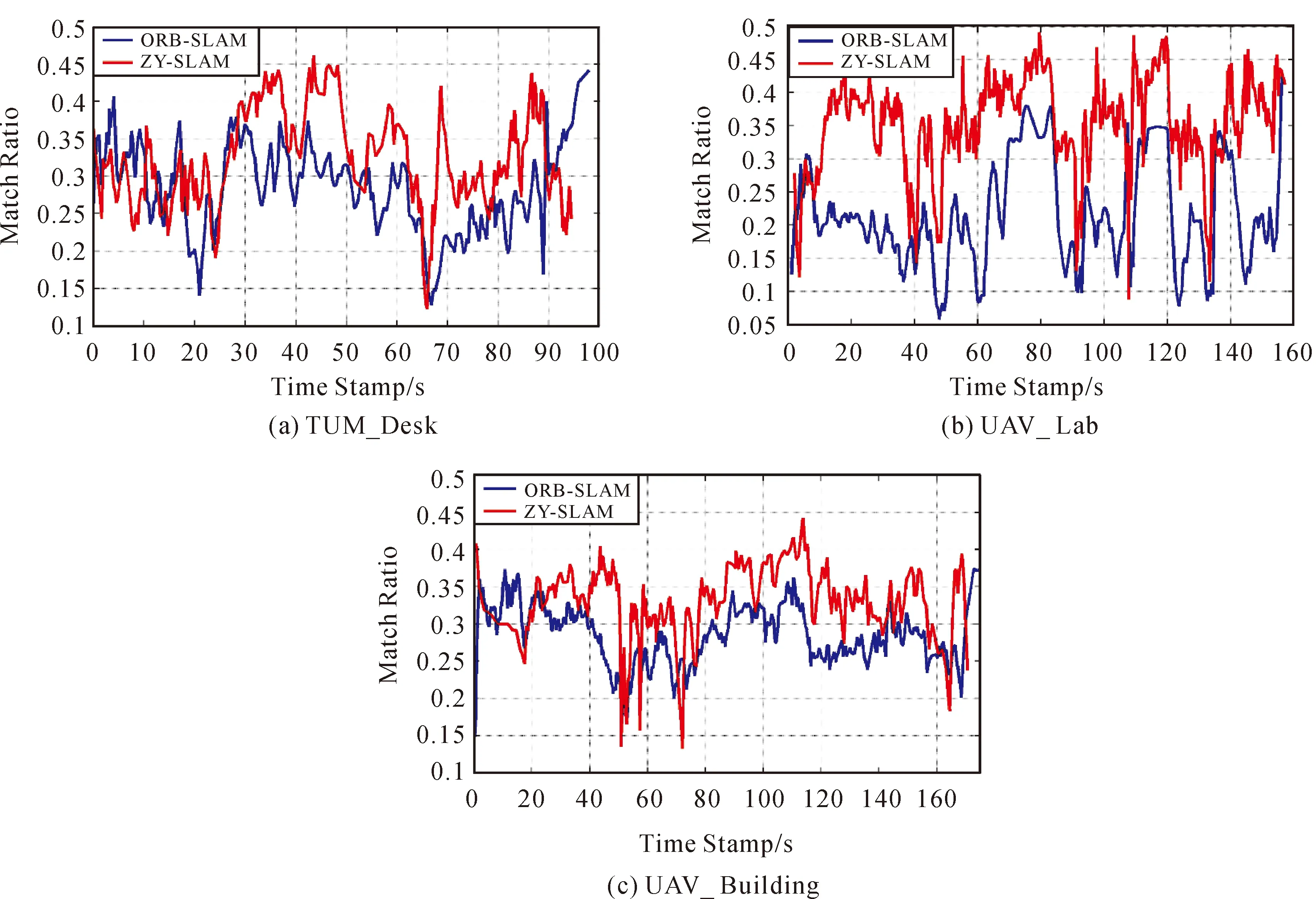
图8 关键帧特征点匹配率Fig.8 Matching ratio of keyframe feature points

图9 相机平面轨迹与地面真值Fig.9 Camera plane trajectories and ground truth
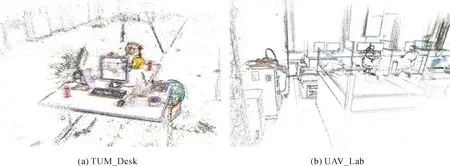

图10 本文方法重建效果Fig.10 Reconstruction examples of proposed method
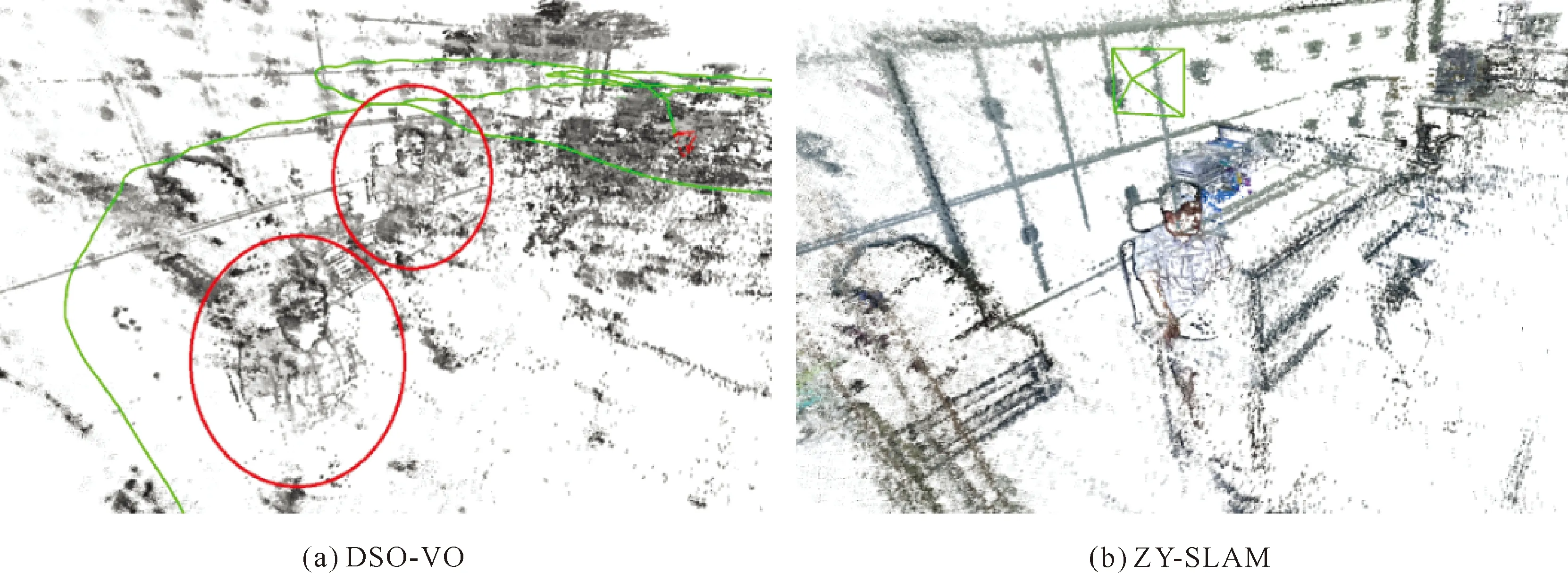
图11 UAV_Lab数据局部重建细节对比Fig.11 Local reconstruction details of UAV_Lab data

图12 UAV_Building数据局部重建细节对比Fig.12 Local reconstruction details of UAV_Building data

