超高压容器爆破压力计算公式的精度比较
2
(1.湖北轻工职业技术学院 机电工程学院,武汉 430070;2.武汉工程大学 机电工程学院,武汉 430205;3.武汉软件工程职业学院 机械工程学院,武汉 430205)
0 引言
计算超高压圆筒容器爆破压力公式的精度,是指公式的理论值与实测爆破压力的符合程度,反映了理论值与实测值的重现性,公式的精度高是指爆破压力理论值与实测值的符合程度高。
对于设计压力大于100 MPa的超高压圆筒容器,可用流变应力公式(Rheological stress formula)或者福贝尔公式(Faupel formula)计算其爆破压力,并采用不同的爆破安全系数确定容器的壁厚[1-4]。构建超高压圆筒容器爆破压力计算公式精度的比较方法,分析流变应力公式与福贝尔公式在其应用范围的精度,拓展公式应用范围或者选择高精度的公式改进超高压圆筒容器设计方法,是值得学术界与工程界关心的课题。
文中应用数理统计知识[5-6],构建超高压容器爆破压力计算公式精度的比较方法,基于36组超高压圆筒容器实测爆破压力范围为220.7~1 326.3 MPa的试验数据[4,7-11],对流变应力公式与福贝尔公式的精度进行分析与比较。
1 建立模型
1.1 总体、样本与个体
1.1.1 计算超高压圆筒容器爆破压力两个公式
计算超高压圆筒容器爆破压力的流变应力公式与福贝尔公式分别为[1-4]:
(1)
(2)
式中u1——爆破压力的流变应力公式计算值,MPa;
Rm——材料抗拉强度,MPa;
η——材料屈强比,η=Rp0.2/Rm;
Rp0.2——材料屈服强度,MPa;
K——容器径比;
u2——爆破压力的福贝尔公式计算值,MPa。
1.1.2 两个公式的应用范围
流变应力公式与福贝尔公式的应用范围是设计压力不低于100 MPa的超高压圆筒容器,即P≥100 MPa。超高压圆筒容器的设计压力P、爆破压力Pb与爆破安全系数nb之间存在如下关系:Pb=nbP≥100nbMPa;采用流变应力公式时,爆破安全系数nb≥2.20[2],对应的爆破压力Pb≥220 MPa;采用福贝尔公式时,爆破安全系数nb≥2.50[1,4],对应的爆破压力Pb≥250 MPa。
根据以上分析,从设计压力的角度流变应力公式与福贝尔公式的应用范围是相同的,但是从超高压圆筒容器爆破压力的角度,流变应力公式与福贝尔公式的应用范围不相同,并且流变应力公式的应用范围比福贝尔公式广。
1.1.3 总体、样本与个体及其关系
从概率论的角度,总体是指在公式应用范围内,所有超高压容器爆破压力实测值与理论值的重现性关系;从数理统计角度,个体是指在满足总体要求时,单个超高压容器爆破压力实测值与理论值的重现性关系,可通过试验得到;符合总体要求的个体集合称为样本,其中个体数量称为样本容量。
显然,总体讨论的对象是无限的,得到的结论具有普适性;虽然样本容量有限,但是构成样本的个体满足总体的要求,因此,通过样本可以对总体的性质(概率分布规律与分布参数等)进行假设检验或者估计。
1.1.4 采用比值法构建随机变量
为了比较流变应力公式与福贝尔公式的精度,在公式应用范围内采用比值法建立如下随机变量:
Ri=Pb/ui(i=1,2)
(3)
式中R1——流变应力公式对应的随机变量;
R2——福贝尔公式对应的随机变量;
Pb——容器实际爆破压力,MPa;
ui——爆破压力的计算值,MPa,当i=1,2时,u1与u2分别为爆破压力的流变应力公式计算值与福贝尔公式计算值。
1.1.5 样本统计
根据以上分析,可将满足公式应用范围的所有超高压容器实际爆破压力视为总体,其中,单个超高压容器实测爆破压力视为个体,若干个个体数据组成样本。虽然流变应力公式与福贝尔公式的应用范围都是设计压力不低于100 MPa的超高压容器,但是两个公式的爆破安全系数不一样,其总体、样本与个体的实际爆破压力范围显然不一样。
对于流变应力公式,总体、样本与个体的实测爆破压力必须满足:Pb≥220 MPa;对于福贝尔公式,总体、样本与个体的实测爆破压力必须满足:Pb≥250 MPa。
用r1与r2分别表示R1与R2的样本,对于第j个个体实测爆破压力,根据式(1)~(3)可得统计量:
ri,j=Pj/ui,j
(4)
式中Pj——第j个个体实测爆破压力,MPa;
ui,j——用第i个公式得到的第j个个体爆破压力的理论值,MPa。
对于容量为mi的样本ri进行统计,可得到样本的准确度及精密度,即:
(5)
(6)

mi——样本ri的容量;
Si——样本ri的精密度。
1.2 公式精度的评价
1.2.1 评价指标
公式精度根据总体的性质,即R1和R2的概率分布规律与分布参数进行评价。当R1与R2基本符合正态分布时,R1的分布参数分别为均值μ1、标准差σ1与变异系数C1,其中:
C1=σ1/μ1
(7)
R2的分布参数分别为均值μ2、标准差σ2与变异系数C2,其中:
C2=σ2/μ2
(8)
准确性与集中性是评价计算公式在其应用范围内精度的两个方面;均值μ1与μ2分别是式(2)与式(3)准确性度量指标,其期望值为“1”;变异系数C1与C2分别是式(1)与式(2)集中性度量指标,其期望值为“0”,由于各种因素的影响,其实际期望值只能是接近“0”的某个正数。变异系数小是均值接近“1”的前提,即其是评价公式精度的最重要指标。
1.2.2 标准差无显著差异的假设检验
根据数理统计知识,用样本r1和r2的统计数据与F假设检验[5-6,12-14],可判断流变应力公式与福贝尔公式在其应用范围的标准差是否有显著差异。显著度为α时,比较σ1与σ2是否有显著差异的检验统计量F为:
(9)
假设R1与R2的标准差无显著差异:σ1=σ2;若F满足:
F1-0.5α(m1-1,m2-1)≤F≤F0.5α(m1-1,m2-1)
(10)
接受标准差无显著差异即σ1=σ2的假设。其中:
(11)
当α=0.02时,文中所用F临界值见表1[5-6]。

表1 分布系数
1.2.3 均值无显著差异的假设检验
当R1与R2的标准差无显著差异时,根据数理统计知识,采用样本数据与t假设检验[5-6],可判断R1与R2的均值是否有显著差异。在公式相同应用范围内及双侧置信度为1-α时,比较均值μ1与μ2是否有显著差异的检验统计量t为:

(12)
假设均值无显著差异:μ1=μ2;如果t满足:
∣t∣ (13) 接受μ1与μ2无显著差异即μ1=μ2的假设。 当α=0.01时,文中所用t临界值见表1[5-6]。 1.2.4 两个随机变量同一性评价 当R1与R2的分布参数同时满足式(10)与式(13)时,表明其标准差σ1与σ2和均值μ1与μ2分别无显著差异,由式(7)与式(8)可知,R1与R2的变异系数也无显著差异,即式(1)与式(2)在相同应用范围的精度相等。 由于R1与R2的标准差σ1与σ2、均值μ1与μ2以及变异系数无显著差异,因此,R1与R2是同一个基本符合正态分布的随机变量。 R1与R2分别基本符合正态分布,是进行公式精度评价的基础,分析其概率分布包括3个内容:一是试验个体的有效性;二是根据样本r1与r2的统计数据,分析R1与R2的分布规律;三是分析R1与R2的分布参数。 1.3.1 试验个体的有效性 试验个体有效性的比较依据[15-16]为: (14) 式中ti,j——第i个公式第j个个体有效性的比较依据。 双侧置信度为1-α时,试验个体有效性的判据为: ∣ti,j∣ (15) 如果ti,j满足式(15),则ri,j在双侧置信度为1-α时有效。 当α=0.005时,文中所用的t分布临界值见表1[5-6]。 1.3.2 分布规律 假设检验是判断R1与R2分布规律的常用方法,具体步骤见参考文献[5-6,17-23]。 1.3.3 分布参数 在自由度为m-1与双侧置信度为1-α时,可根据样本r1与r2的统计数据分析随机变量R1与R2分布参数的取值区间。 (1)R1分布参数取值区间。 R1均值μ1的取值区间[5-6]为: μ1∈[μ1min,μ1max] (16) 其中: (17) (18) 式中t1-0.5α,m1-1——单侧置信度为1-0.5α时的t分布系数。 r1标准差σ1的取值区间[5-6]为: σ1∈[σ1min,σ1max] (19) 其中: (20) (21) 当α=0.02时,文中所用的t与χ2分布系数见表1[5-6]。 (2)R2分布参数取值区间。 R2均值μ2的取值区间[5-6]为: μ2∈[μ2min,μ2max] (22) 其中: (23) (24) 式中t1-0.5α,m2-1——单侧置信度为1-0.5α时的t分布系数。 R2标准差σ2的取值区间[5-6]为: σ2∈[σ2min,σ2max] (25) 其中: (26) (27) (3)分布参数的优化。 当R1与R2的分布参数同时满足式(10)与式(15)时,表明R1与R2是同一个基本符合正态分布的随机变量R,R分布参数的取值区间应是R1与R2取值区间的公共部分。 根据以上分析,R均值μ的取值区间为: μ∈[μmin,μmax] (28) 其中: μmin=max(μ1min,μ2min) (29) μmax=min(μ1max,μ2max) (30) R标准差σ的取值区间为: σ∈[σmin,σmax] (31) 其中: σmin=max(σ1min,σ2min) (32) σmax=min(σ1max,σ2max) (33) R变异系数C的取值区间为: C∈[Cmin,Cmax] (34) 其中: Cmin=σmin/μmax (35) Cmax=σmax/μmin (36) 文献[4,7-11]中提供的36组超高压圆筒容器实测爆破压力范围为220.7~1 326.3 MPa的样本,依次按实测爆破压力从小到大列入表2。 表2 超高压圆筒容器爆破压力试验样本及统计 对于流变应力公式,将36组试验数据的准确度与精密度数据代入式(14)与式(15),可知∣t1,j∣ 对于福贝尔公式,将序号为4~36的33组试验数据的准确度与精密度数据代入式(14)与式(15),可知∣t2,j∣ 表3 分布规律的统计 取显著度为0.05,由自由度3查表1,可得到皮尔逊统计量临界值为7.815。 由于样本r1与r2的皮尔逊统计量之和分别为6.690 8与6.023 5,均小于临界值7.815,因此假设成立,即R1与R2分别是基本符合正态分布的随机变量。 根据以上分析,在显著度为0.05时,R1与R2是基本符合正态分布的随机变量,可用式(9)~(13)进行R1与R2均值与标准差比较。 4.1.1 标准差比较 假设R1与R2的标准差无显著差异:σ1=σ2;将表2统计数据代入式(9),可得:F=0.896。 由m1=36与m2=33,查表1得F0.99(35,32)=0.443,F0.01(35,32)=2.290,因此,F满足式(10),即: F0.99(35,32) 在α=0.02,即双侧置信度为98%时,接受假设,R1与R2的标准差σ1与σ2无显著差异。 4.1.2 均值比较 因为R1与R2的标准差无显著差异,由式(12)可得:t=1.290。 由m1=36与m2=33以及α=0.01,查表1可得:t0.99,67=2.654;均值μ1与μ2是否存在显著差异比较依据t满足判据式(13),即满足∣t∣≤2.654,因此,在α=0.01,即双侧置信度为98%时,R1与R2的均值μ1与μ2无显著差异。 在双侧置信度为98%时,用流变应力公式与福贝尔公式计算超高压圆筒容器的爆破压力,随机变量R1与R2的均值μ1与μ2以及标准差σ1与σ2分别无显著差异。根据式(7),(8)可知,其变异系数C与C1或C2无显著差异,因此,在对应的应用范围内,流变应力公式与福贝尔公式的精度相同。 以上分析还表明,R1与R2是同一个基本符合正态分布的随机变量。 将表1,2数据代入式(16)~(27),在双侧置信度为98%时,可得到R1与R2分布参数的取值区间。 R1均值与标准差的取值区间分别为: μ1∈[1.004 4,1.069 0] (37) σ1∈[0.061 24,0.107 8] (38) R2均值与标准差的取值区间分别为: μ2∈[0.975 4,1.047 2] (39) σ2∈[0.064 05,0.115 8] (40) 由于R1与R2可视为基本符合正态分布的同一随机变量R,因此,将式(37)~(40)代入式(28)~(36),可分别得到R均值、标准差与变异系数的取值区间: μ∈[1.004 4,1.047 2] (41) σ∈[0.061 24,0.107 8] (42) C∈[0.058 48,0.107 3] (43) 应用数理统计与概率论知识,构建了超高压圆筒容器爆破压力计算公式精度的评价指标与比较方法。基于36组超高压圆筒容器实测爆破压力样本,分析比较了流变应力公式与福贝尔公式在其应用范围的精度。 (1)双侧置信度为99.5%时,对于流变应力公式,文中超高压圆筒容器实测爆破压力范围为220.7~1 326.3 MPa的样本,36组个体试验数据是有效的;对于福贝尔公式,文中超高压圆筒容器实测爆破压力范围为255.1~1 326.3 MPa的样本,33组个体试验数据是有效的。 (2)显著度为0.05时,36组超高压圆筒容器实测爆破压力与流变应力公式之比,以及33组超高压圆筒容器实测爆破压力与福贝尔公式理论值之比,分别是基本符合正态分布的随机变量。 (3)双侧置信度为98%时,以上两个随机变量分布参数的均值与标准差分别无显著差异,可视为同一个基本符合正态分布的随机变量;该随机变量的均值位于1.004 4~1.047 2之间,标准差位于0.061 24~0.107 8之间,变异系数位于0.058 48~0.107 3之间。 (4)对于设计压力不低于100 MPa的超高压圆筒容器,采用流变应力公式(爆破安全系数不小于2.20)与福贝尔公式(爆破安全系数不小于2.50)进行基于爆破压力的壁厚设计计算具有相同的精度。1.3 概率分布


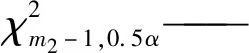

2 试验样本与个体有效性
2.1 试验样本与统计


2.2 个体有效性分析
3 分布规律

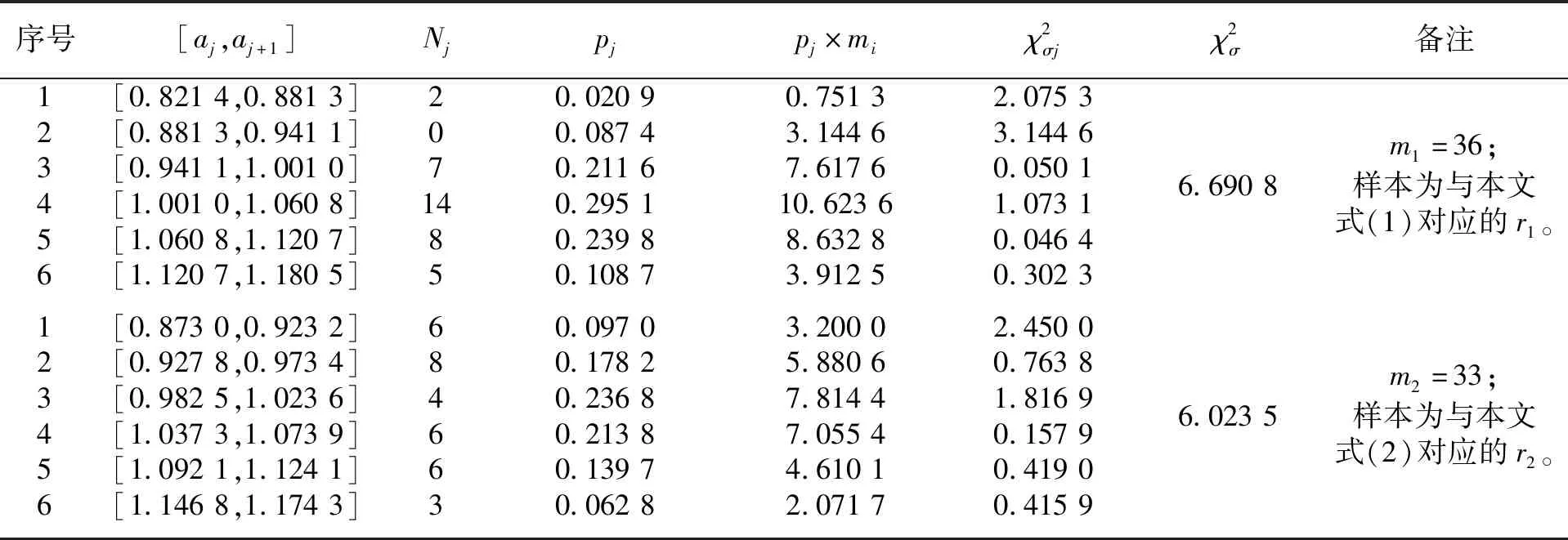
4 精度的比较与评价
4.1 精度比较
4.2 精度评价
5 分布参数的取值区间及其优化
6 结语

