同心圆排布管束流体弹性不稳定性模拟研究

(天津大学 化工学院，天津 300350)

0 引言

管壳式换热器具有服役环境广泛、工作可靠等优点，在换热设备中占有率可达到70%以上。随着对提高传热效率的要求越来越高，换热设备逐渐大型化、换热管束无支撑跨距增大、流体流速加快，使流体诱导振动问题日益突出，管束因振动失效引发的严重事故增多。引起换热管束振动的主要因素是管外的流体冲击[1-3]，横向流诱导管束振动的机理包括湍流抖振、漩涡脱落、流体弹性不稳定性和声振动[4]。许多国内外学者[5-9]对此进行了大量数值模拟和试验研究，认为在横流速度较低时，容易产生周期性的漩涡脱落而产生振动；当横流速度较高时，一般是由流体弹性不稳定性激发换热管的振动。流体弹性不稳定性是最常见且最具破坏性的流致振动机理，在工程中应重点关注。

同心圆排布管束主要应用于核工业中，但针对该类型换热器的流体诱导振动研究较少，也没有相应的标准指导设计。本文通过建立同心圆排布管束不同位置处的局部模型，采用计算流体力学(CFD)和流固耦合(FSI)的方法，研究同心圆排布管束的流体弹性不稳定性；根据数值模拟结果，分析不同位置处振动幅度、临界流速和主振方向等特征，以期为同心圆排布管束的换热器设计和运行维护提供参考。

1 数值模拟计算模型

1.1 物理模型

在本文研究的同心圆排布中，60°为最小重复单元，且在0°～60°排布形式关于30°线对称分布，如图1所示，故只需研究0°～30°不同位置处管束振动，便可得到同心圆排布换热器管束整体振动状态。为此建立了3个局部模型，其排布方式分别为类正方形排布、过渡排布和类三角形排布，如图2所示。管束外径25 mm，同心圆排布径向和周向间距分别为33.6，36.4 mm，并将模型中心管分别命名为管A、管B和管C。在管束分布前延长流场范围以形成均匀来流，在管束后延长流场范围用来观察尾流。

图1 同心圆排布示意

图2 同心圆排布管束物理模型

1.2 流固耦合模型

在计算流体力学方法基础上，采用弹簧刚体结构与动网格技术，建立流固耦合模型。研究中近似认为管束为不可变形的刚体，对管束施加弹簧约束，模拟管板处支撑结构对管束振动的约束。考虑到流体阻尼对管束振动的影响，对管束运动施加阻尼力，先从每次迭代中提取换热管振动速度，然后乘以阻尼系数、以力的形式反馈到迭代计算。

由于换热管长径比较大，建立实际轴向尺寸的模型网格数多、计算时间长，故在数值模拟时通常利用周期性条件简化管束结构。但漩涡扩展是三维结构，需要一定的轴向空间来反映其流动特性，所以轴向尺寸的取值较有争议。吴皓等[10]对轴向尺寸为d(d为换热管外径)和2d的模型计算结果进行了对比，认为d的轴向尺寸已能够反映流体弹性不稳定性发生时流场的基本特征，故本文取轴向尺寸为d。

1.3 数值计算模型

根据周期性条件，将管束横截面设置为对称面边界，在类正方形排布、过渡排布、类三角形排布中分别设置25,22，23根弹性管，其余换热管设置为刚性管，如图3所示。弹性管设置为弹簧刚体结构并建立独立坐标系，在弹性管顺流及横流方向设置监测点，以便于测量管束在流体力作用下的振幅。入口条件设置为均匀来流，来流速度从0.1 m/s起递增设置；出口条件设置为压力出口。其他主要边界条件及计算设定见表1。

图3 同心圆排布管束数值模拟模型

表1 边界条件与相关计算设置

通过对比类正方形排布模型在0.1 m/s流速下，不同网格尺寸计算得到的管A的均方根振幅来验证网格无关性。网格尺寸分别为0.5,1.0,2.0,3.0 mm，对应网格数量为4.53×106,1.67×106,6.1×105,2.3×105。不同网格尺寸下,管A横流方向均方根振幅如表2所示，可以看出，当网格尺寸大时，均方根振幅响应与网格数相关性较大；但随着网格尺寸减小、网格数增多，均方根振幅变化不大，2.0 mm尺寸以下网格结果相差小于1%，可认为对计算结果无影响。故本文综合考虑计算精度和计算量，选择尺寸为2.0 mm的网格进行计算。

表2 不同网格尺寸下管A均方根振幅

2 管束流体弹性不稳定性研究

2.1 流场分析

管束振动流体弹性不稳定性现象研究最为关注的是流场内的速度分布，故对3种排布的速度分布云图进行分析，如图4所示(其中,U为管间间隙流速，m/s；f为管的固有频率，Hz；d为管外径，m；U/(fd)为无因次间隙流速)。

(a)类正方形排布(U/(fd)=2.632)

(b)过渡排布(U/(fd)=2.391)

(c)类三角形排布(U/(fd)=2.525)图4 不同排布形式速度场云图

由图4可以看出，流体速度在管束附近发生较大变化，在来流方向与管束背流方向速度小;在换热管上下两侧速度值较大，这是因为流体流过换热管时发生边界层分离现象,在管束尾部均有类似卡门涡街的尾流，但形状不规则。

速度场云图可以反映不同位置处速度大小的分布，但各点速度的方向并不能体现，故对3种排布的流场的流线进行了比较，如图5所示。由不同排布方式可以看出，类正方形排布的管束流场最为规整，管束之间的流道类似于正方排布；过渡排布的流线由于流道形状影响，出现向一侧偏移的现象，管束一侧受到流体冲刷；类三角形排布呈现明显的对称性,管束两侧流线分布均匀。

(a)类正方形排布(U/(fd)=2.632)

(b)过渡排布(U/(fd)=2.391)

(c)类三角形排布(U/(fd)=2.525)图5 不同排布形式流线图

2.2 临界流速分析

在类正方形排布、过渡排布和类三角形排布中，分别将位于模型中间的管A、管B和管C作为研究对象，管A，B，C位置见图2。根据数值模拟结果得到均方根振幅与管束外径比值和无因次间隙流速的关系，如图6所示。

图6 均方根振幅与无因次间隙流速关系曲线

临界流速是研究管束流体弹性不稳定性的一个重要参数，以均方根振幅值达到换热管外径2%时的间隙流速作为临界流速。在前期工作中，通过水洞试验对同心圆排布管束的流体弹性不稳定性进行了相关研究[11]，该试验通过高速摄影对同心圆排布管束在不同流速下的振幅进行了测量研究,具体试验装置见文献[11]。试验研究的同心圆排布与模拟模型的管径、管间周向和径向间距均相等，通过对数值模拟模型中的弹簧刚体结构参数设置，保证数值模拟模型与试验模型刚度相同。

本文将数值模拟结果同水洞试验结果进行了对比，不同排布形式的管束临界流速与试验值见表3。试验值与模拟值存在差异，首先是因为模拟计算时，为减少计算量，模型轴向长度取为d=25 mm，试验所用模型轴向长度为350 mm，虽然保证了相同刚度，但流体沿模型轴向方向具有相关性，仍会对结果有影响；其次，不同模型上下边界处对流体流动的影响会引起间隙流速的误差(如图2所示)，试验研究时通过设置挡板降低此影响；此外，试验装置安装配合也会使测量值产生误差。

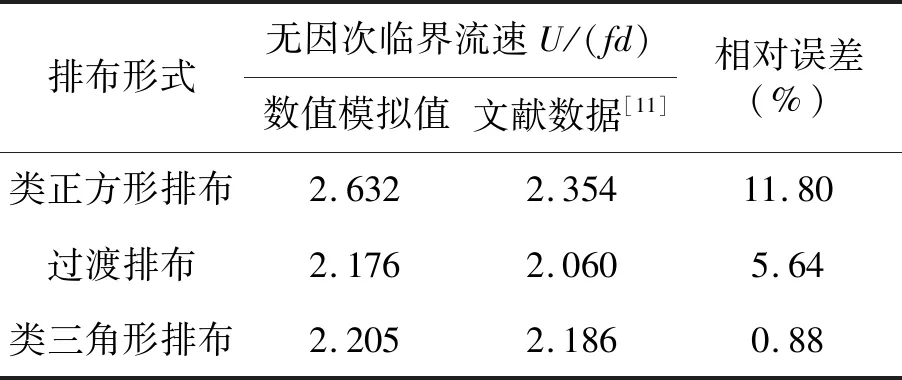
表3 不同排布形式管束临界流速

由表3可以看出，对于3种不同排布形式，过渡排布区域无因次临界流速最小，为2.176；类正方形排布区域临界流速最大，为2.632。即在管束同心圆排布方式中，过渡排布区域管束最不稳定；类正方形排布区域管束最为稳定。本文认为这与3种排布形式的对称性有关，过渡排布为非对称结构，在流场中受横流方向的力使其偏离平衡位置，易导致流体弹性不稳定性现象，故其临界流速较小；类正方形排布与类三角形排布均为对称结构，受此影响小。

2.3 主振方向分析

通过MATLAB软件绘制管束轨迹图，分析管束振动的主振方向，不同排列形式的管束在不同无因次间隙流速下的管束轨迹见图7。其中顺流方向与来流方向相同，横流方向与来流方向垂直。

(a)类正方形排布

(b)过渡排布

(c)类三角形排布图7 不同排布管束轨迹

由图7中可以看出，当间隙流速较小时，管束主振方向为顺流方向；随着间隙流速增大，管束主振方向变为横流方向，对于过渡排布与类三角形排布也有同样变化。该主振方向的变化与以前学者[12-14]的研究结果相同。吴皓[12]在研究正方形排布管束流体弹性不稳定性时，发现随着间隙流速的增大，管束主振方向由顺流方向变为横流方向，他认为这与来流及尾流的变化及不同间隙流速下的主要激振机理有关。间隙流速较小时主要为湍流抖振；随着间隙流速增大，主要振动原因变为流体弹性不稳定性。对于3种排布形式，随间隙流速增大，过渡排布处最先出现主振方向变化，说明此位置最先出现流体弹性不稳定现象。

3 结论

本文针对同心圆排布换热器管束流体弹性不稳定性，采用数值模拟的方法进行了研究。通过对同心圆排布管束几何排布特点分析，建立了代表不同位置的3个模型；通过对管束的流固耦合振动分析，得到了发生流体弹性不稳定性时的临界流速、主振频率、主振方向等特征，并得到如下结论。

(1)从流场的分析结果可知，类正方形排布区域的管束间的流场最为规整；过渡排布区域的管束间的流道出现明显的偏移现象；类三角形排布区域的管束间的速度场分布呈现对称性。

(2)同心圆排布管束不同位置处，临界流速不同；类正方形排布管束临界流速最大，为2.632；过渡排布管束临界速度最小，为2.176。即同心圆排布管束中过渡排布处最易失稳，在同心圆排布设计制造及维护中应重点关注该位置。

(3)同心圆排布不同位置处，管束振动主振方向均随间隙流速发生变化，随着间隙流速的增大，管束主振方向由顺流方向变为横流方向；过渡排布处最先出现主振方向的变化，这与过渡排布处临界流速最小相对应。