空间引力波探测任务的入轨误差分析

李 卓，王有亮，郑建华，李明涛*

(1.中国科学院 国家空间科学中心，北京 100190；2.中国科学院大学，北京 100039)

1 引 言

2016年，美国地基激光干涉引力波天文台(LIGO)第一次完成地面引力波信号探测，检验了广义相对论的正确性，也预示人类可以通过引力波探测来认识宇宙结构和天体的演化。为了扩展引力波探测频段，对0.01 mHz～1 Hz左右中低频引力波进行探测，需要开展空间引力波探测活动。空间引力波探测任务具有更宽广的视野和大量的波源，涉及的关键技术包括无拖曳控制，高精度激光测距，微推进技术，大尺度高稳定编队构型设计等[1]。

20世纪90年代开始美国国家航空航天局(NASA)和欧洲航天局(ESA)共同提出了空间激光干涉引力波探测项目LISA(Laser Interferometer Space Antenna)，旨在观测由超大质量黑洞合并和由中子星或黑洞组成的双星系统所产生的引力波[2]。LISA任务包括3个航天器，在地球轨道后方20°左右位置共同构成臂长为2.5×106的等边三角形。利用空间自由悬浮测试质量块作为传感器，将引力波信号转化为测试质量块间距变化的信号，也是干涉仪臂长的变化[3]。

中国科学家也提出了类似的引力波探测项目，其中包括太极计划和天琴计划。太极计划由位于等边三角形顶端的三颗卫星组成，旨在探测中低频波段的引力波。太极计划的主要科学目标是观测双黑洞并合和极大质量比天体并合时产生的引力波辐射，以及其它的宇宙引力波辐射过程[1]。中山大学也提出了天琴计划，天琴计划在距地球105km的近圆轨道内放置三颗航天器形成等边三角形，来验证引力波在中低频的存在和地球重力测量等其他观测内容[4-5]。

空间引力波探测通常会维持四年以上任务周期，由于初始入轨误差等不确定扰动的存在，使构型发生变化，可能导致其不再满足任务要求。因此需要对误差传播进行分析。已知常用的方法有Monte-Carlo法，通过抽样实验统计状态量的均值和标准差。Monte-Carlo法原理简单，对各种误差普遍适用，然而为得到准确值需要进行多次抽样，当任务周期长时，计算量大，耗时长。

对于非线性误差传播分析问题，可以运用协方差分析方法，混沌多项式展开法，状态转移张量法，微分代数方程法，高斯混合模型法，解Fokker-Plank 方程等方法解决[6]，工程实际中非线性误差通常符合正态分布形式，需要根据实际情况选择合适的方法。线性协方差方法多用于分析动力学模型为线性函数的轨道预报、交会、转移等问题，可快速获得误差传播结果[7]。已有的研究结果可以解决线性模型下的空间引力波探测误差传播问题[8]，对于非线性模型，可用协方差分析描述函数法(CADET)解决。CADET法对非线性函数进行统计线性化，然后通过积分计算状态变量的均值和协方差矩阵。不同于Monte-Carlo法的耗时长和线性协方差法的精度低，CADET方法计算速度快且精度高，适用于空间引力波探测轨道误差分析问题。

本文运用CADET方法分析了空间引力波探测任务构型在入轨误差下的稳定性，并研究了位置误差和速度误差的大小和方向对构型稳定性的影响。

2 空间引力波探测任务动力学模型

选取J2000日心惯性坐标系作为参考坐标系，航天器受到太阳引力及其他天体的摄动力。卫星在空间运动中主要受太阳引力及水星、金星、地球、火星、木星、土星、天王星、海王星和冥王星的摄动力作用。以LISA为例，对于相同初始条件，考虑以上所有力的作用时，其臂长变化约为2.9×105km，当去掉金星、地球、木星的作用时，臂长变化分别变为2.4×105km，2.0×105km，2.7×105km；而去掉其他天体作用时臂长变化仍然保持在2.9×105km左右。因此为简化模型，只考虑金星、地球、木星的摄动力[8]。空间引力波探测任务动力学模型表示为[9]:

(1)

其中，Rk表示三颗卫星的位置矢量，k=1,2,3。Ri表示金星、地球和木星的位置矢量，i=1,2,3。μ0表示太阳引力常数，μi分别表示金星、地球和木星的引力常数，i=1,2,3。

定义Rij(t)=Rj(t)-Ri(t),(ij=12,23,31)为卫星之间的相对位置矢量。卫星编队动力学指标分别为臂长L，呼吸角θ，臂长变化率V，星地距离D，可用公式(2)～(5)表达。

Lij(t)=‖Rij(t)‖ ,

(2)

(3)

(4)

D(t)=‖Re(t)-Rc(t)‖ ,

(5)

其中：Re是地球位置矢量，Rc是三卫星中心位置矢量。

3 CADET在空间引力波探测任务轨道误差分析中的应用

若x(t)是系统状态向量；F(t)是系统状态矩阵，无过程扰动的线性连续随机系统微分方程是:

(6)

(7)

p(t)=E[δx(t)δxT(t)] ,

(8)

(9)

根据第二节，本文的动力学模型是非线性系统，可以表示为：

(10)

其中，x(t)是方程的状态变量，x1～x18为卫星1,2,3的位置速度；x19～x21为臂长，x22～x24为呼吸角，x25～x27为臂长变化率；x28为星地距离。运用CADET方法分析入轨误差对空间引力波探测任务的影响，需对系统进行统计线性化。

(11)

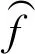
(12)

式(12)的计算比较复杂，工程中常常用如下方法简化：

已知f(x)关于x一阶可微，在m进行f(x)的一阶泰勒展开，得

(13)

忽略一阶泰勒余项R1(x)，求式(13)期望值，f(x)的线性化形式是

(14)

动力学方程的描述函数N为[12]

(15)

其中，I为28×28的单位矩阵，n为

(16)

式中，f1至f28包括下列方程：f1至f18为卫星1，2，3的位置速度；f19至f21为臂长L12，L13，L23；f22至f24为呼吸角θ1，θ2，θ3；f25至f27为臂长变化率V12，V13，V23；f28为星地距离D。

n的具体形式是

(17)

其中，

(18)

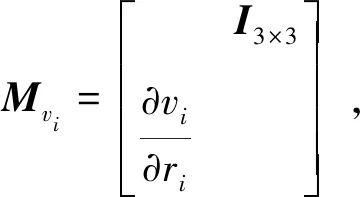
(19)

i(i=1,2,3)的速度对位置的偏导。

(20)

(21)

其中:K包括臂长L、呼吸角θ、臂长变化率V和星地距离D，其中ij=12,13,23，k=1,2,3。

根据CADET方法知，具有初始误差，空间引力波探测任务航天器在J2000日心惯性坐标系中的状态均值与协方差的微分方程如下[11]:

(22)

其中，初始条件m0包括三卫星初始位置速度和臂长、呼吸角、臂长变化率和星地距离，p0为对角线矩阵，数值由三卫星初始位置和速度误差决定，N(t)由式(15)～(21)求出。根据以上条件，可通过积分求出任意时刻的均值和协方差矩阵。

4 CADET仿真验证

基于动力学模型，以任务周期内一直满足指标要求为标准选择合适的位置速度初始条件，并加入正态分布误差。分别用CADET法和Monte-Carlo法求任务周期10年内构型的臂长，呼吸角，臂长变化率和星地距离的均值和标准差。

图1给出了CADET法和Monte-Carlo法求出的均值和标准差随时间变化的结果。其中圆圈为Monte-Carlo法抽样仿真1 000次结果，实线为CADET法结果。由图1可知，两种方法结果一致，以Monte-Carlo法的仿真结果作为标准，可以认为CADET法是有效的。

图1 CADET法和Monte-Carlo法的对照结果Fig.1 Comparison diagrams of CADET and Monte-Carlo

任务过程中将产生大量数据，所以选取一个特殊点(10年周期内的最后时刻的数据)进行分析。考虑初始误差时CADET法和Monte-Carlo法均值、标准差误差和相对误差如表1所示。

由表1可知，臂长均值相对误差不超过0.017 8%，标准差相对误差不超过5.600 4%；呼吸角均值相对误差不超过0.014 5%，标准差相对误差不超过4.780 2%；臂长变化率均值相对误差不超过1.633 6%，标准差相对误差不超过5.339 7%；星地距离均值相对误差不超过0.028 8%，标准差相对误差不超过2.833 7%。说明CADET方法对于空间引力波探测误差分析问题确实准确有效。

表1 CADET法和Monte-Carlo法结果比较Tab.1 Results comparison of CADET and Monte-Carlo methods

5 基于CADET的空间引力波探测轨道误差传播分析

在空间引力波探测任务过程中，航天器面临的入轨误差是不确定的，不同的入轨误差会对构型产生不同程度的影响。当使用Monte-Carlo法分析入轨误差对构型影响的不确定性时，需要多次抽样保证结果的可靠性，因此解决问题的过程将花费大量时间。现在已知CADET方法对于空间引力波探测误差分析问题准确有效，可以运用CADET方法进行误差传播分析。

航天器的入轨误差主要分为位置误差和速度误差，下面将对这两类误差对构型指标产生的影响进行分析。以空间引力波探测任务为例，臂长要求为3×106km，呼吸角变化小于1°，臂长变化率小于10 m/s，星地距离小于6.5×107km时可认为构型满足空间引力波探测任务要求。初始 构型如图2所示，1、2、3曲线分别代表卫星1、2，卫星1、3，卫星2、3之间的指标变化情况，其中臂长最大值为3.014×106km，呼吸角最大值为60.37°，臂长变化率最大值为3.325 m/s，标准差均为0。

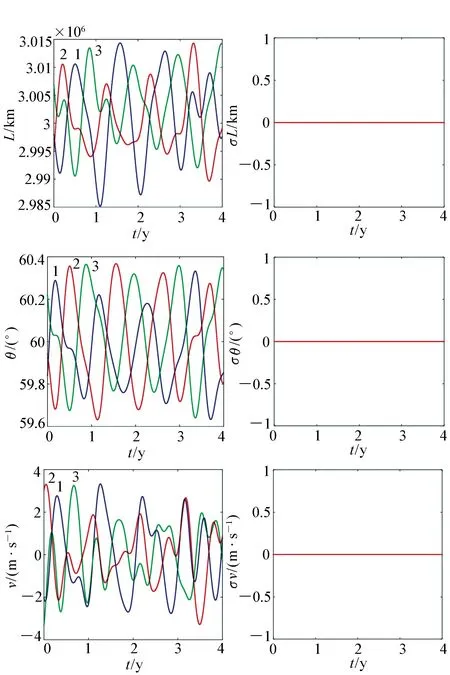
图2 初始构型Fig.2 Initial constellations

5.1 误差方向对构型的影响

(1)不同方向的位置误差

当同时向3颗卫星增加大小相等的位置误差时，误差的方向对构型产生显著影响。径向误差使构型标准差产生的变化远大于其他两个方向的误差。径向位置误差增加了卫星的势能，所以构型产生的扰动更大。因此，航天器发射时需优先考虑减小径向位置误差。

(2)不同方向的速度误差

同时向卫星1,2,3增加均值为1 cm/s，方向分别沿径向，切向和法向的正态分布的速度误差，构型变化如表3所示。

当同时向3颗卫星增加大小相等的速度误差

表2 位置误差方向对构型的影响Tab.2 Effect of position error direction on constellation

表3 速度误差方向对构型的影响Tab.3 Effect of velocity error direction on constellation

时，误差的方向对构型产生显著影响。切向误差使构型标准差产生的变化远大于其他两个方向的误差。切向速度误差增加了卫星的动能，所以构型产生的扰动更大。因此，航天器发射时需优先考虑减小切向速度误差。

5.2 误差大小对构型的影响

(1)不同大小的位置误差

因为径向位置误差对构型影响最大，因此在本节中仅以径向位置误差为例分析误差大小对构型的影响。

首先以任务周期4年为例，同时向卫星1,2,3增加正态分布的径向位置误差，误差均值分别为100 km，1 000 km，构型变化表4所示。

同时向三颗卫星增加径向位置误差时，位置误差对构型的影响不明显。当误差均值为100 km和1 000 km时，只考虑均值时构型指标满足要求，但观察标准差发现，1 000 km时标准差增大，构型发散不满足指标要求。

表4 误差大小对构型的影响(周期4年)Tab.4 Effect of error magnitude on constellation(T=4 years)

(2)不同大小的速度误差

因为切向速度误差对构型影响最大，因此在本节中仅以切向速度误差为例分析误差大小对构型的影响。

同时向卫星1,2,3增加正态分布的切向速度误差，误差均值分别为1 cm/s，10 cm/s，构型变化如表4所示。

向三颗卫星同时增加相同方向速度误差时，速度误差对构型的影响不明显。当误差均值为1 cm/s和10 cm/s时，只考虑均值时构型指标满足要求，当误差均值为10 cm/s时虽然标准差增大，但由于任务周期短，构型发散程度小，仍然满足指标要求。

为比较周期4年和10年时误差大小对构型的影响，对周期为10年的情况重复上述仿真，结果如表5所示。当位置误差为100 km和速度误差为1 cm/s时构型满足指标要求；当位置误差为1 000 km和速度误差为10 cm/s时构型不满足指标要求。当比较任务周期为4年和10年两种情况，发现标准差大小随时间增加，任务周期延长时，大小相等的入轨误差会使构型产生更大扰动。

表5 误差大小对构型的影响(周期10年)Tab.5 Effect of error magnitude on constellation(T=10 years)

5.3 三星间相对误差方向对构型的影响

当航天器发射存在入轨误差时，三卫星误差的相对方向可能会对构型产生不同的影响。下文将探究相对方向相反的入轨误差对构型产生的影响。

(1)相对方向相反的位置误差

以任务周期4年为例，分别向三卫星径向、切向、法向施加均值为100 km的正态分布的，相对方向相同和相反的位置误差，构型变化如表6所示。

表6 相对位置误差方向对构型的影响Tab.6 Effect of direction of relative position error on constellation

由于增加的位置误差大小相等，方向相反，构型标准差相同，反向误差的扰动大于同向误差。当航天器受到的位置误差相对方向不同时，构型产生的扰动更大。

(2)相对方向相反的速度误差

分别向三卫星径向、切向、法向施加均值为10 cm/s的正态分布的，相对方向相同和相反的速度误差，构型变化如表7所示。

表7 相对速度误差方向对构型的影响Tab.7 Effect of direction of relative velocity error on constellation

由于增加的速度误差大小相等，方向相反，构型标准差相同，反向误差的扰动大于同向误差。当航天器受到的速度误差相对方向不同时，构型产生的扰动更大。

无论是位置误差还是速度误差，当航天器受到的误差相对方向相同时，误差对构型的影响明显小于误差相对方向相反时的情况。这也为任务入轨工作带来一些启示，如果无法减小入轨误差的绝对值，可以通过使三卫星受到的误差保持相同方向，减小入轨误差对构型的影响，保证后续任务顺利完成。

5.4 位置速度误差对构型的影响

入轨位置误差和速度误差通常同时存在，方向也可能不同，因此下文将分析两种不同方向的误差同时存在对构型产生的影响。以周期4年为例，使切向速度误差由0.5 cm/s逐渐增加至3 cm/s，并调整径向位置误差的大小，以臂长在3×106±3.5×104km内为标准，记录使构型发散的位置误差临界点，如图3所示。

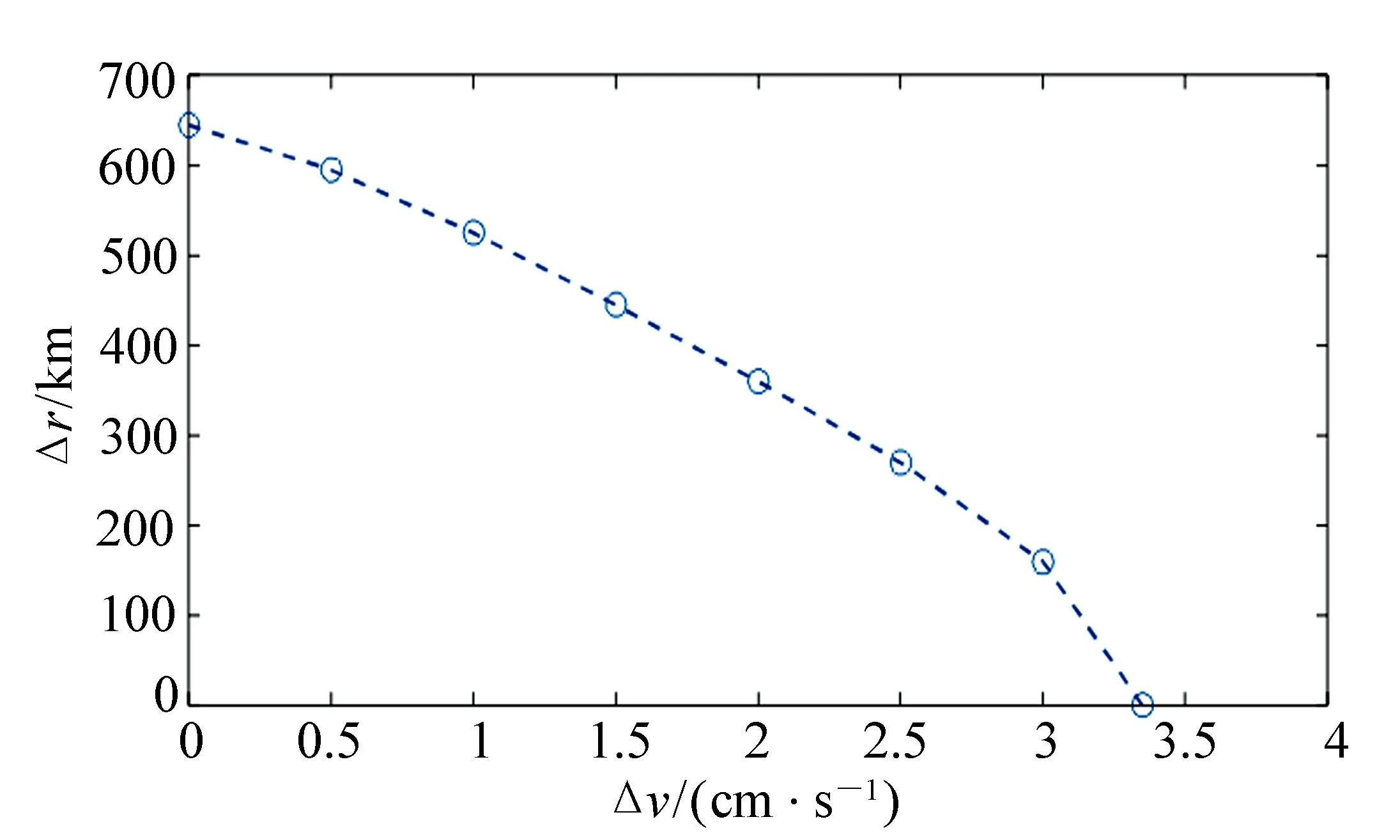
图3 位置误差与速度误差的关系Fig.3 Relationship between position error and velocity error

由图3可知，速度误差的影响大于位置误差，对于同一构型，当速度误差增大时，为满足指标要求需减小位置误差。当速度误差是0.5 cm/s，位置误差将超过595 km时构型发散；当速度误差是3 cm/s，位置误差超过160 km时构型发散。

6 结 论

本文首先介绍了空间引力波探测任务的动力学模型；运用CADET法提出了空间引力波探测任务入轨误差传播方程；进行CADET方法仿真和Monte-Carlo法仿真，并比较二者结果；以本文构型为例，运用CADET方法对入轨误差的影响进行分析。仿真结果表明：

(1)以Monte-Carlo法结果为标准，CADET法在10年任务周期内与其相对误差不超过6%， CADET法可以进行有初始误差情况下的任务过程的误差传播分析；

(2)在相同环境下完成Monte-Carlo法1 000次抽样运算平均用时约为15 min，而CADET法平均用时不超过1 min， CADET法可以实现任务过程中对误差传播的快速预测，用时远小于Monte-Carlo法。

(3)径向位置误差和切向速度误差分别改变了卫星的势能和动能，对空间引力波探测任务构型影响较大。当误差的相对方向相同时，对构型的影响小于相对方向不同时，可以通过保持误差方向相同减小入轨误差对构型的影响。当周期为4年且同时存在两种误差时，位置误差不超过160 km，速度误差不超过3 cm/s时，构型仍满足指标要求。