中承式钢管混凝土拱桥地震易损性分析

卓卫东，颜全哲,2，吴梅容,3，谷 音

(1. 福州大学 土木工程学院，福建 福州 350108；2. 福建省公路管理局，福建 福州 350004；3. 福建船政交通职业学院 道路工程系，福建 福州 350007)

钢管混凝土拱桥因解决了拱桥高强度材料应用和施工两大难题，近年来在我国公路和高速铁路大跨径桥梁建设中得到了大量应用[1]。然而，由于缺乏结构地震破坏数据及试验数据，迄今为止，其抗震性能尚未完全明确。为从概率的角度定量地描述其抗震性能，宏观地反映地震动强度与结构破坏程度之间的关系，本文针对中承式钢管混凝土拱桥结构体系，探讨建立其地震易损性曲线。

结构地震易损性通常定义为结构在给定强度的地震作用下达到或超过某一极限状态(性能水平)的条件概率[2-3]；地震易损性曲线则表示结构在不同强度的地震作用下达到或超过某一性能水平的概率曲线。目前，结构地震易损性曲线可通过经验法[4]、试验法[5]和理论分析法[6-7]等得到。由于目前大跨径桥梁结构的地震破坏数据和抗震试验还极少，所以，理论分析法往往是得到其地震易损性曲线的唯一可行方法，并常采用增量动力分析(IDA)法或改进的IDA法建立其地震易损性曲线。谷音等[8]、吴文朋等[9]均采用IDA方法，建立高墩大跨连续刚构桥梁的地震易损性曲线；房慧明等[10]则采用拉丁超立方抽样(LHS)与IDA相结合的方法(LHS-IDA法)，探讨建立了一座高墩大跨连续刚构桥梁的地震易损性曲线；刘震等[11-12]采用同样方法，探讨了近场及远场地震动作用下中承式钢管混凝土拱桥的结构易损性。沈国煜等[13]将人工神经网络(ANN)、正交设计法(ODM)及蒙特卡洛抽样法(MC)相结合，发展了可同时考虑结构地震需求和能力的随机性以及地震动的随机性的复合随机地震易损性分析方法，并用于计算斜拉桥的地震易损性。

尽管钢管混凝土拱桥在我国已得到大量工程应用，然而，针对其地震易损性的研究还极少。本文以中承式钢管混凝土拱桥为研究对象，通过调查统计158座已建成实桥的设计资料，建立其典型桥梁样本，并采用IDA方法建立其理论地震易损性曲线。考虑到中承式钢管混凝土拱桥构件众多，其易损部位及其破坏模式一般无法直接判断，为此，本文分两个步骤进行分析：(1)首先，建立线弹性结构模型，进行静力分析和不同强度地震作用下结构地震响应分析，确定各构件在地震组合下的易损部位；(2)其次，建立合理的桥梁非线性力学模型，进行IDA分析，确定其损伤概率。

1 桥梁样本及其有限元模型

1.1 典型桥梁样本

中承式钢管混凝土拱桥的结构体系主要有单跨有推力体系和多跨无推力体系[1]。基于文献[1]和文献[14]，对国内已建成的158座跨径不小于50 m的中承式钢管混凝土拱桥的设计资料进行统计分析。结果表明，其主拱跨径中位数为150 m，矢跨比的常用范围在1/4～1/5之间，且以1/5居多；宽跨比集中在0.05～0.25之间。对于三跨无推力体系，其边跨与主跨的跨径比常在0.164～0.424之间，边拱矢跨比的常用范围在1/4.6～1/9.8之间，且与主拱的矢跨比之比集中在1/1.16～1/1.2之间。拱轴系数集中在1.167～1.5之间，且拱轴线形超半数采用悬链线；大部分主拱肋采用桁架式截面，且钢管采用Q345钢材(约占统计样本的83%)，钢管中填充的混凝土多采用C40或C50，少量采用C55或C60；拱肋之间均设置横向支撑，吊杆一般采用平行柔性吊杆，支座系统主要采用板式橡胶支座，部分桥梁在肋间横梁处设置滑板支座。

根据统计分析结果，以三跨无推力体系作为研究对象，建立中承式钢管混凝土拱桥的典型桥梁样本。典型桥梁样本的跨径布置为(40+150+40) m，桥面宽33 m；主跨平行设置两片钢管混凝土拱肋，横向轴间距为19.5 m；两片拱肋之间共设置5道“一”字型风撑，风撑纵向间距20 m。主拱肋矢跨比f/L=1/5，拱轴线型为悬链线，拱轴系数m=1.3；采用四肢钢管桁架式断面，截面尺寸为3.65 m×2.10 m，标准段弦杆采用φ850×14 mm钢管，拱脚至桥面段采用φ850×16 mm，腹杆采用φ350×10 mm无缝钢管；各钢管均采用Q345C钢焊接连接。主拱肋的上、下弦管内均灌注C50混凝土，在拱脚段外包C50混凝土。吊杆纵向间距5 m，吊索为121丝φ7高强平行钢丝束；拉杆布置于吊杆横梁内，采用φ120的40Cr钢拉杆；拱肋系杆采用6束由37根直径15.24 mm的环氧喷涂钢绞线外套PE构成索体。两侧边跨为上承式钢筋混凝土悬臂半拱，边拱矢高比f/L=1/8.097，拱轴线型为悬链线，拱轴系数m=1.3；采用劲性骨架混凝土结构，截面尺寸为2.6 m×2.5 m。主桥墩和边墩均采用群桩基础。在交接墩处设置GPZ6DX盆式橡胶支座；在车行道板下设置板式橡胶支座。

1.2 有限元模型

典型桥梁样本的有限元空间动力计算模型见图1。全桥空间模型共有2 953个节点、4 620个单元。

图1 典型桥梁样本的有限元动力模型

在进行线性时程分析时，拱肋弦杆、腹杆以及风撑均采用弹性梁单元模拟；根据GB 50936—2014《钢管混凝土结构技术规范》的相关规定[15]，计算拱肋钢管混凝土弦杆的单元截面特性。桥面系等效为由纵梁和横梁组成的梁格体系，不考虑桥面铺装的刚度贡献，仅考虑其质量效应。吊杆采用只受拉的杆单元模拟，系杆单元采用具有初始应力的拉杆单元模拟；采用刚性连接单元模拟单向盆式支座，释放支座的纵向约束；采用弹簧单元模拟桥面板下的板式橡胶支座。主桥墩、承台设置为刚性连接，考虑其质量贡献；边跨拱肋、桥墩、立柱也均采用弹性梁单元模拟，墩下群桩基础用桩-土弹簧模拟，特性值由“m”法计算。在进行非线性时程分析时，墩柱采用纤维梁单元模拟；其中钢筋采用双折线型随动硬化本构模型，混凝土采用Mander建议的约束混凝土本构模型。

在动力计算模型中，采用了经典的瑞利阻尼矩阵，并假定各阶模态阻尼比均为0.05。根据结构动力特性分析结果，利用第1阶和第8阶自振频率确定瑞利阻尼的系数α、β。

2 地震动输入

根据1.1节的调查统计结果，修建中承式钢管混凝土拱桥的场地条件主要为Ⅰ类、Ⅱ类场地。因此，在本文分析中，选取了美国太平洋地震研究中心(PEER)Ⅰ类、Ⅱ类场地各100条远场地震动记录作为地震响应时程分析的输入，以考虑地震动的随机性。

本文采用IDA方法来形成理论地震易损性曲线，以峰值加速度PGA作为地震动的强度指标；输入地震动的PGA变化范围为0.05g～0.6g，共分为12级，各级加速度峰值增量为0.05g；分别对Ⅰ类、Ⅱ类场地，同时沿顺桥向(纵向)、横桥向和竖向3个方向逐级输入100条经过调幅的地震动加速度时程，进行地震反应时程分析，计算工况总数达4 800个。

3 构件性能水平定义

3.1 主拱肋易损部位与破坏准则

(1) 主拱肋易损部位的确定

本文所选的典型桥梁样本为三跨无推力中承式钢管混凝土拱桥，由于主拱肋构造复杂，其易损部位和破坏模式均需要通过试算确定。这里，以PGA调幅到0.2g的3条Ⅰ类场地典型的地震动输入为例说明试算过程。

首先，进行地震动调幅，将PGA调为0.2g；之后，对结构进行线性时程分析和反应谱分析；反应谱分析时，振型组合采用CQC法，并取前200阶振型进行组合。根据线性时程分析和反应谱分析结果，进一步计算主拱肋上、下弦管在地震组合下的内力包络曲线，并分析其易损部位。限于篇幅，这里仅列出主拱肋上弦管在地震组合下的内力包络曲线，见图2、图3。在水平顺桥向和竖向地震动组合影响下，主拱肋上弦管最大轴力出现在与第2、4道横撑相交的截面，最大竖向弯矩出现在拱脚截面；在水平横向和竖向地震动组合影响下，主拱肋上弦管最大轴力出现在拱顶截面，最大竖向弯矩和横向弯矩均出现在拱脚截面。

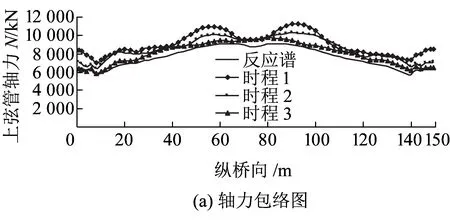
图2 上弦管内力包络图(水平顺桥向+竖向地震动)

同理，根据下弦管内力包络图可以得出，在水平顺桥向和竖向地震动组合影响下，下弦管最大轴力出现在拱脚截面，最大竖向弯矩出现在拱脚截面以及拱肋与桥面相交的截面位置；在水平横向和竖向地震动组合影响下，下弦管轴力、竖向弯矩和横向弯矩的最大值均出现在拱脚截面；此外，在拱顶与横撑相交的下弦管截面，竖向弯矩和横向弯矩较大。

可见，在地震组合作用下，主拱肋的易损部位主要出现在拱脚、拱顶截面以及与横撑相交的几个截面位置。

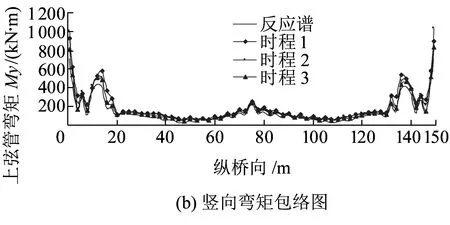
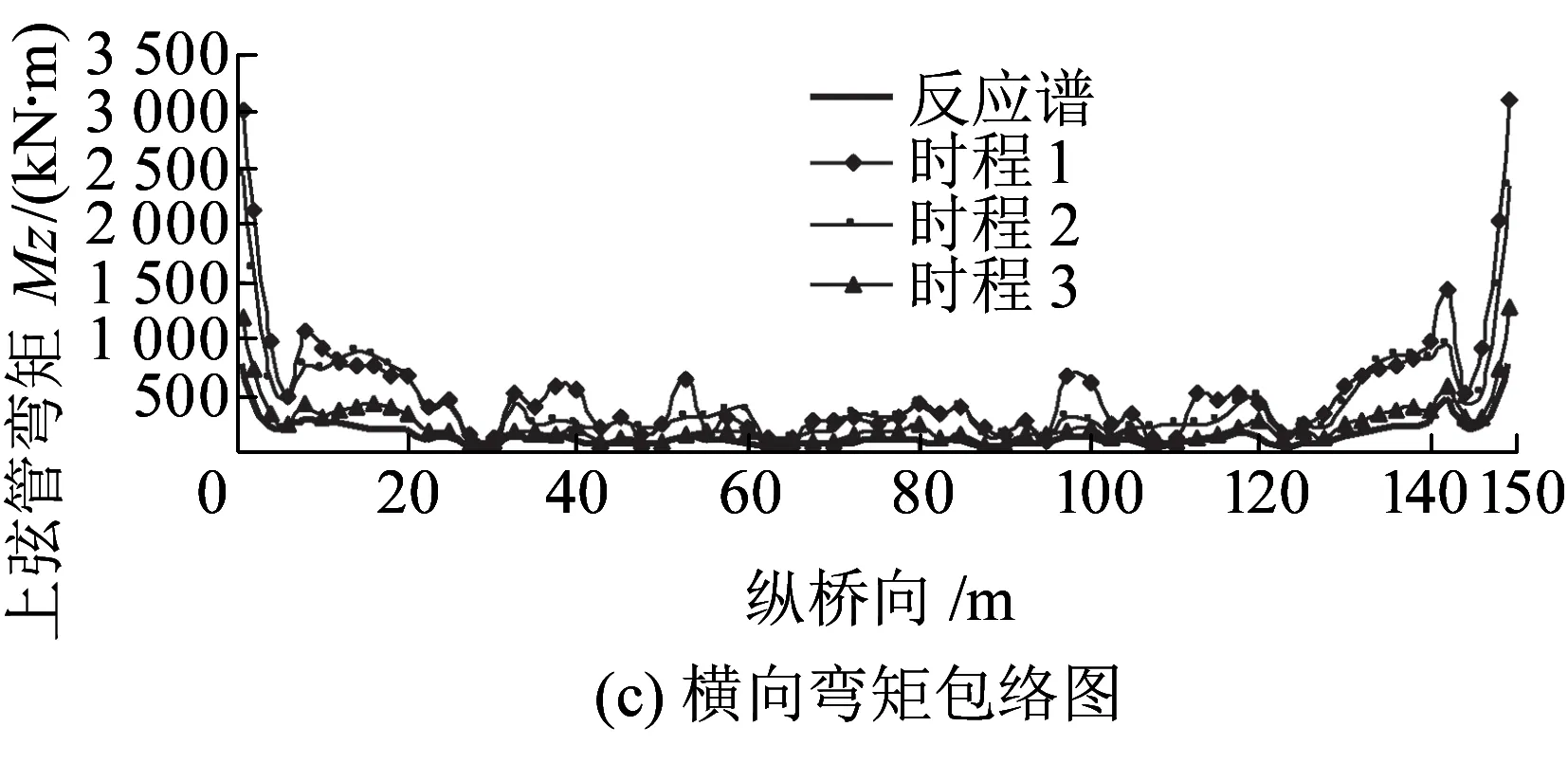
图3 上弦管内力包络图(水平横桥向+竖向地震动)

(2) 主拱肋破坏准则

为减少计算工作量，采用强度准则作为钢管混凝土拱肋(弦管)初始损伤准则。假定钢管混凝土材料为理想弹塑性材料，采用统一理论，建立考虑双向弯矩、扭矩、轴力相互作用的屈服面方程(强度准则)[16]为

(1)

式中：Nu为单轴受压构件的极限压力值；Mu为极限弯矩，对应的是钢管最大纤维应变达到10 000×10-6时的弯矩；Tu为极限扭矩。Nu、Mu和Tu分别可参考文献[15]计算。

利用式(1)，可判断主拱肋各易损部位是否屈服；若拱肋屈服，可进一步考虑其材料非线性影响。

3.2 墩柱性能水平定义

震害资料表明，钢筋混凝土桥墩往往是桥梁结构体系中的易损构件，其破坏模式主要有弯曲破坏、弯剪破坏和剪切破坏等。试算分析表明，本文桥梁样本的交接墩为易损构件，其易损部位为墩底截面。

由于本文采用纤维梁单元模拟墩柱，因此，可直接选取墩柱控制截面的钢筋和混凝土材料应变作为其损伤指标，并量化定义其不同的性能水平。墩柱各级性能水平定义及其量化描述见表1。

3.3 吊杆与系杆破坏准则

本文桥梁样本中的吊杆和系杆均为只能承受轴向拉力的杆件，因此，吊杆和系杆的破坏模式为受拉破坏；在分析时取设计容许拉力、屈服强度和极限抗拉强度分别作为吊杆、系杆的第一、第二和第三损伤状态的强度指标。

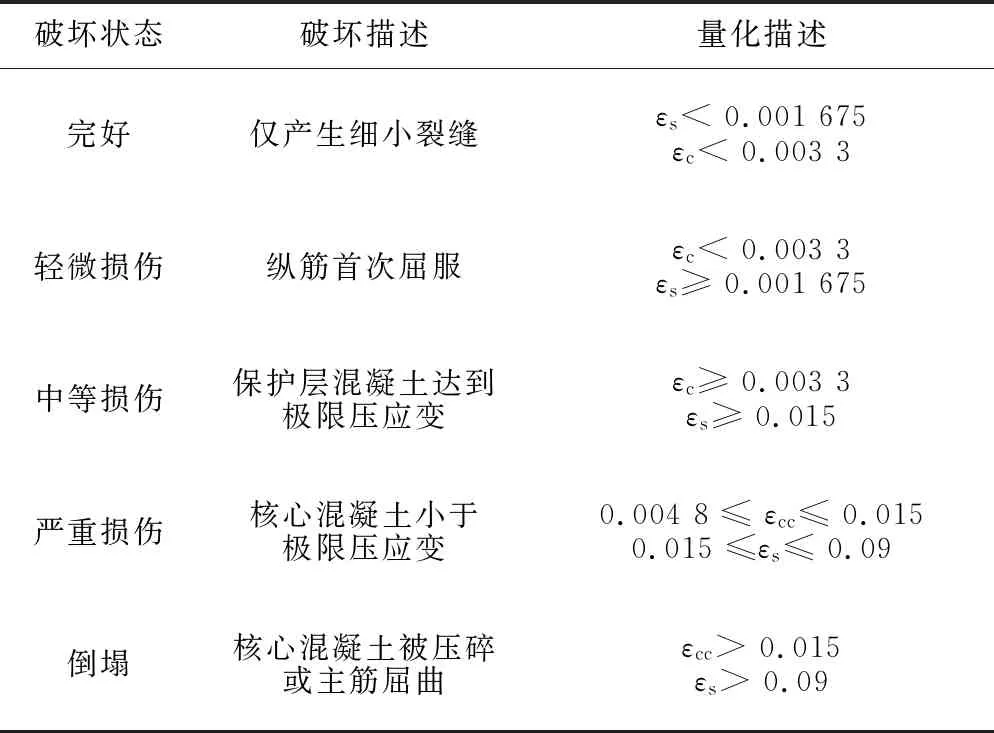
表1 墩柱性能水平定义

注：εc为保护层混凝土压应变；εs为钢筋拉应变；εcc为核心混凝土压应变。

3.4 支座破坏准则

支座也是桥梁结构体系中较易遭受损伤的构造之一，其破坏模式主要有失稳破坏和强度破坏。对盆式橡胶支座，可采用强度准则或位移准则定义其破坏准则。根据JT/T 391—2009《公路桥梁盆式橡胶支座》[17]，确定本文桥梁样本所采用的支座的破坏准则，见表2。

表2 支座破坏准则

3.5 基础破坏准则

基础是桥梁结构体系中的关键构件，通常按能力保护构件设计。因此，其破坏准则一般采用强度准则，具体可按照现行JTG 3362—2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》的相关规定进行计算[18]。

4 地震易损性曲线

本文假定各构件损伤的概率均服从对数正态分布，因此，构件损伤的概率密度函数可表示为如下的对数正态分布函数的形式为

(2)

采用 MATLAB中的Lsqcurvefit函数来求解损伤的概率密度函数的均值与标准差，从而最终可以得到损伤概率分布。

根据IDA分析结果，本文桥梁样本的钢管混凝土拱肋在各级地震动作用下均未出现损伤，桩基础也始终处于弹性反应范围；吊杆和系杆由地震作用所引起的应力增量与恒载作用引起的应力相比基本可以忽略；仅交接墩和盆式橡胶支座发生损伤。

对于大跨径中承式钢管混凝土拱桥，欧洲规范[19]指出在恒载和设计地震作用下，拱桥的轴压比较高，塑性铰区的延性设计可能不可靠；故本文在建立样本桥梁交接墩的地震易损性曲线时，仅考虑轻微损伤和中等损伤这两级损伤状态。

Ⅰ类和Ⅱ类场地条件下交接墩和盆式橡胶支座损伤的概率分布函数的统计参数分别见表3、表4，交接墩和支座损伤的概率分布与假定的对数正态分布符合良好，说明采用该假定进行构件地震易损性分析是合理的。

表3 构件损伤概率分布函数的统计参数(Ⅰ类场地)

表4 构件损伤概率分布函数的统计参数(Ⅱ类场地)

根据式(2)，绘出了盆式橡胶支座和交接墩在不同场地条件、不同的地震动作用方向组合下的地震易损性曲线，分别见图4～图6。这里需要指出的是，在形成图4所示支座的理论地震易损性曲线时，假定在不同强度水平的地震动作用下，桥梁样本只有盆式橡胶支座损伤而其它构件(包括交接墩)均没有损伤；在形成图5和图6交接墩的理论地震易损性曲线时，则假定在不同强度水平的地震动作用下，桥梁样本只有交接墩损伤而其它构件(包括支座)均没有损伤。

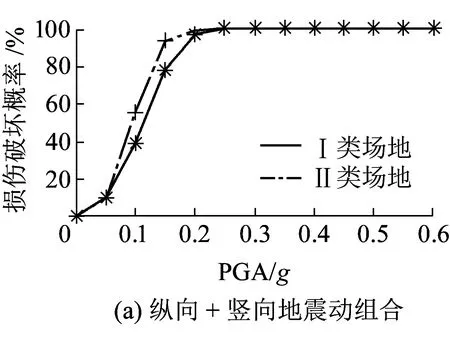
图4 盆式橡胶支座地震易损性曲线

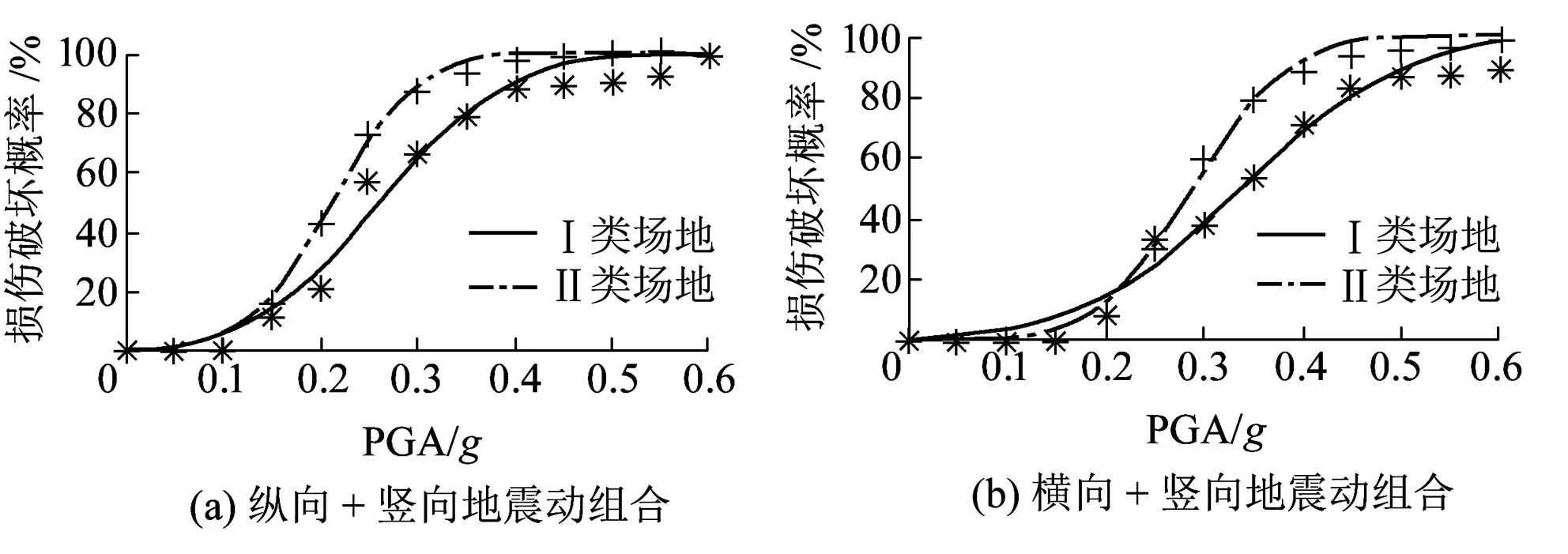
图5 与交接墩轻微损伤相应的地震易损性曲线

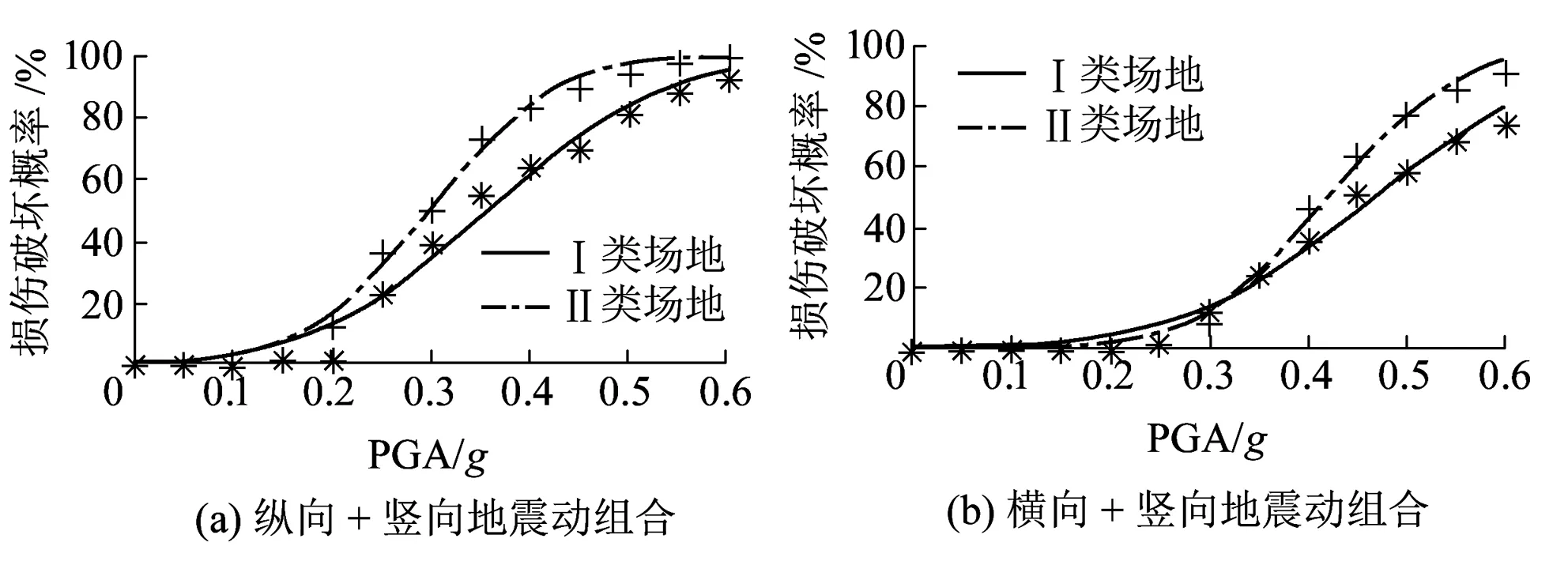
图6 与交接墩中等损伤相应的地震易损性曲线

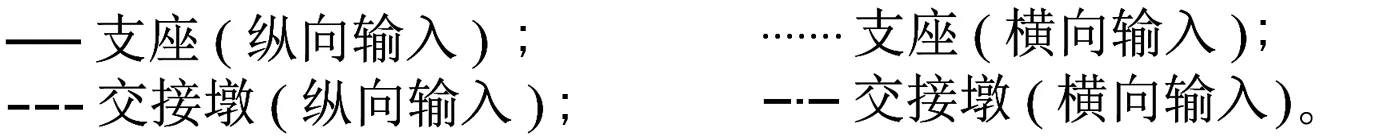
Ⅰ类、Ⅱ类场地条件下盆式橡胶支座与交接墩的地震易损性曲线的比较情况见图7。由图7可知，对本文分析的典型桥梁样本，两种场地条件下、各个不同强度水平的地震动作用引起的支座损伤概率均大于交接墩的损伤概率；这说明对于典型的三跨无推力中承式钢管混凝土系杆拱桥，在交接墩处设置的盆式橡胶支座是最先损伤的结构部件。

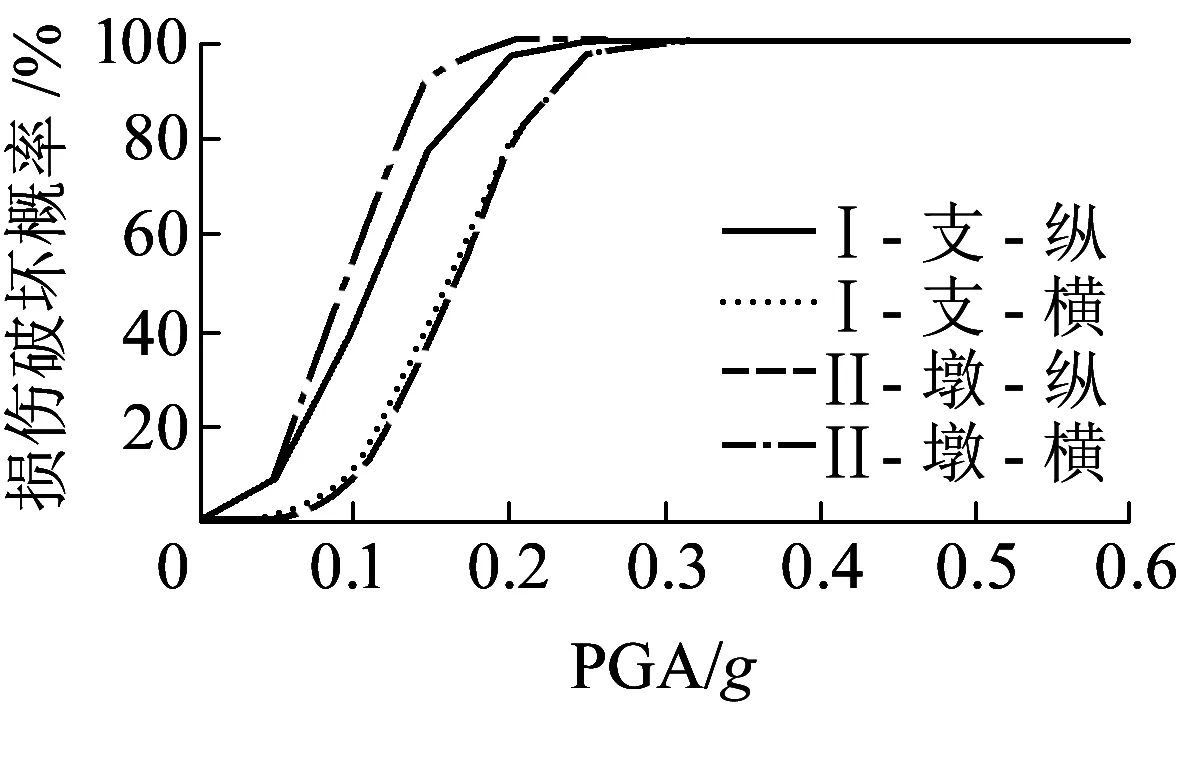
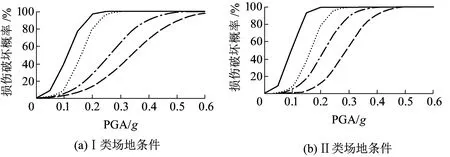
图8 场地条件及地震动方向组合对支座易损性曲线的影响

场地条件及地震动方向组合对盆式橡胶支座和交接墩损伤概率的影响见图8～图10。图8～图10中，符号“Ⅰ”、“Ⅱ”分别表示Ⅰ类和Ⅱ类场地；“纵”表示纵向+竖向地震动组合，“横”表示横向+竖向地震动组合。由图8可知：在水平纵向+竖向地震动组合影响下，Ⅱ类场地条件下盆式橡胶支座和交接墩的损伤概率均高于Ⅰ类场地条件，而且地震动强度越大，场地条件的影响也越大；在水平横向+竖向地震动组合影响下，场地条件变化对盆式橡胶支座的损伤概率几乎没有影响；不管是在Ⅰ类还是Ⅱ类场地条件下，水平纵向+竖向地震动组合影响下交接墩的损伤概率均高于水平横向+竖向地震动组合影响下的损伤概率。这表明对于典型的三跨无推力中承式钢管混凝土系杆拱桥，顺桥方向是地震影响较不利的方向，这一点与过去破坏性地震中调查到的其它桥型的震害现象是一致的。

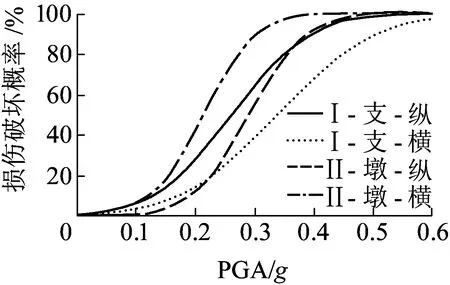
图9 场地条件及地震动方向组合对交接墩易损性曲线的影响(轻微损伤)

图10 场地条件及地震动方向组合对交接墩易损性曲线的影响(中等损伤)

5 结论

本文采用IDA分析方法，进行典型的三跨无推力中承式钢管混凝土系杆拱桥地震易损性分析，结果表明：

(1) 钢管混凝土拱肋具有较高的地震强度安全储备，一般不会因地震作用而出现损伤；吊杆和系杆由地震作用引起的应力增量基本可以忽略，因此，它们也不会因地震作用而破坏。

(2) 交接墩及其上设置的盆式橡胶支座是三跨无推力体系中的主要易损构件，且支座更易损。对桥梁样本的损伤概率分析表明，地震易损性分析中假定构件损伤概率服从对数正态分布是合理的。

(3) 对三跨无推力体系，顺桥方向是地震影响较不利的方向；与Ⅰ类场地条件相比，Ⅱ类场地条件下结构的损伤概率相对较高，而且地震动强度越大，场地条件的影响也越大。

(4) 在输入地震动PGA从0.05g变化到0.6g时，本文分析的桥梁样本的桩基础始终处于弹性反应范围，符合能力保护构件的设计要求。