基于运输时效性的技术站车流组织优化方法研究

万鑫兴 ，张春民，殷 洁

WAN Xinxing1, 2, ZHANG Chunmin2, YIN Jie2

（1.中国铁路兰州局集团有限公司 银川车站，宁夏 银川 750011；2.兰州交通大学 交通运输学院，甘肃 兰州 730070）

(1.Yinchuan Station of China Railway Lanzhou Group Co.， Ltd.， Yinchuan 750011， Ningxia， China； 2.School of Transportation， Lanzhou Jiaotong University， Lanzhou 730070， Gansu， China)

0 引言

随着国家供给侧改革及经济社会的转型，以机械、电子、轻纺、食品、工业产成品及包裹和快件为代表，快捷运输对送达时间有特殊性要求比重越来越大[1]，而我国铁路车流组织模式依然是以解决运输能力紧张为主，兼顾运输时间的传统模式[2]，这种模式已经不能适应我国铁路运输时效性低下与运量急需增长之间的矛盾，使铁路运输增长幅度不能与运量增长幅度相协调[2-4]。赵娟[5]、刘晓伟等[6]分别重点考虑运输服务需求和车流时空分布进行了车流组织优化，取得较好结果，但没有针对铁路运输时效性进行深入探讨。此外，铁路车辆在车站周转或停留的时间约占总运输时间的70%[7]，而有调中转在我国主要编组站的集结停留时间约占中转车总停留时间的40% ~ 50%[8]。随着我国高速铁路网的形成，普速铁路的运能得到了极大的解放[4]，技术站车辆集结时间将成为限制普速铁路运能的瓶颈。

针对目前的技术站车流组织模式，对进入技术站集结的车辆，根据车辆来源特征，考虑不同解编车辆来源所需要的集结时间不同，将编组车辆分为以下3类。第一类车辆，从装车站(专用线、货场或物流中心等)通过小运转或摘挂列车直接取送至技术站的车辆。这类车辆的去向较多，而且车辆数不多且零散，集结时间具有一定的随机性[9]。第二类车辆，来自于另一技术站的中转车列中的区段或直通列车中的车辆，其特点是去向相对较少，且车辆数较多。这类车辆集结较易做到满轴满重的运输条件，集结时间相对较短，编组作业较为简单。第三类车辆，到达该技术站需摘挂和小运转列车运送的车辆，这类车辆的特点是卸车站为本技术站临近的其他中间站，需要按照站顺或组顺进行编组，集结过程涉及较少，但编组作业环节较复杂。第一类车辆与第二类车辆涉及到了集结时间，在目前技术站集结时间的理论计算中，2类车辆在技术站需要集结的时间均可通过集结参数进行估算。而在实际生产中，针对某一车辆而言，车辆集结时间和集结次数受到其他同方向车流数量的影响，而其他同方向车流数量的决定因素则更为复杂，这就造成不同车辆集结时间的巨大差异，进而严重影响运输时效性。因此，压缩目前车流组织方式的车辆集结时间，是优化技术站车流组织的一个重要方法[10]。

1 基于运输时效性的技术站车流组织优化方法

为达到最大限度地利用铁路运输能力的目的，需要技术站优化集结等待车辆的时间。由于等待集结时间有一定的随机波动性，导致运输时效性不高。因此，基于运输时效性，提出技术站车流组织优化应采用车流运动集结法。车流运动集结法是指在同一径路的前提下，以动态的车流预报信息为基础，以压缩单个车辆在所有技术站的等待集结时间为手段，进而优化车流组织的方法。该方法利用车流在各技术站间运动的过程，即时连挂各技术站的第一类车辆以不断增加车组的数量，同时利用车流在技术站短暂的停留时间，与各列车进行车流组号的换挂重组，以便随时达到技术直达列车的组织条件。进而实现技术站列车编组计划中分组列车与单组列车的充分协调，从而实现节约运输时间的目的[11-13]。

1.1 单个技术站

单个技术站车流运动集结法的实质是利用其他技术站乃至整个相关区段的车流相对本技术站在运动的过程中进行车流集结计算，以达到节约车流组织中集结等待时间的目的，而这种方法类似于换挂列车在技术站的技术作业，因而考虑将中转列车的组织方式通过车流运动集结法改变为换挂列车组织方式。其中，中转列车的技术作业相比换挂列车的技术作业，节约的时间可以表示为

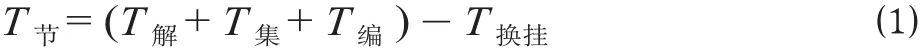
式中：T节为换挂列车比中转货物列车节约的时间；T解为列车解编作业时间；T集为列车等待集结时间；T编为列车编组时间；T换挂为列车换挂作业时间。

T换挂是技术站在车流运动集结法的组织情况进行的，换挂作业应比正常换挂作业复杂，所需时间也会相应增加，但其作业复杂程度一般不应大于T编，因而单个技术站车流运动集结法是可以节约运输时间的。

采用车流运动集结法后，技术站的中转货物列车的新编组内容，应在该列车到达前，根据车流运动集结法提前计算准备，以便列车到站直接组织换挂重组作业，而不是进行解体、统计现车后再编组出发。单个技术站车流运动集结法组织方式示意图如图1所示。

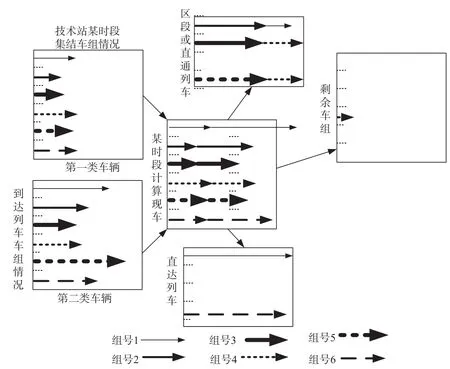
图1 单个技术站车流运动集结法组织方式示意图Fig.1 Schematic diagram of organizational mode of “traffic flow motion aggregation method” for single technical station

从图1中可以看出，“第一类车辆”为技术站某时段现车集结情况；“第二类车辆”为将要到达技术站的途中车辆；“某时段计算现车”为“第一类车辆”和“第二类车辆”汇合后预设的集结情况；“区段或直通列车”“剩余车组”及“直达列车”是根据“某时段计算现车”依据列车优先级别顺序推算所得编组方案。单个技术站车流运动集结法实施规则如下。

（1）第一类车辆在与第二类车辆同组号的车辆连挂后，恰好达到满重满轴的条件，则组织技术直达列车发出；超出满重满轴的条件的，将超出车流挂于相邻组号(相邻到站)的列车发车，如组号1将超出部分挂于组号2车流之后；达不到满重满轴条件的，欠重欠轴不多的，则组织列车欠轴发车，如组号6车流组织欠轴技术直达列车。

（2）第一类车辆在与第二类车辆同组号的车辆连挂后，达不到满重满轴条件，且欠轴过多的，如组号2，3，4，5车流连挂情况，则将相邻组号(相邻到站)的车辆连挂组织区段或直通列车，如组号3车流与组号4车流、组号4车流与组号5车流的连挂情况；连挂后如超出满轴满重的条件，则甩出最近时间到达技术站的车组，将其留在技术站继续等待集结，如图组号4车流与组号5车流连挂后，将部分组号4车流甩出留在技术站等待集结。

（3）第一类车辆在与第二类车辆同组号的车辆连挂后，达不到满重满轴条件时，将相邻组号(相邻到站)的车辆连挂组织区段或直通列车，仍然不能达到满轴满重的条件时，且其欠轴不多，则组织欠轴的区段或直通列车，如组号2车流与组号1车流的连挂组织情况；欠轴较多的，则考虑连挂其他相邻组号(相邻到站)使其达到满轴满重的条件。

（4）第一类车辆在与第二类车辆同组号的车辆连挂后，达不到满重满轴条件时，将相邻组号(相邻到站)的车辆连挂组织区段或直通列车，仍不能达到满轴满重的条件，且其欠轴过多，且考虑连挂其他相邻组号(相邻到站)仍不能达到满轴满重的条件的，则考虑将更多组号车流连挂组织满轴或欠轴的区段列车。

1.2 技术站间

单个技术站车流运动集结法仅针对某一技术站的车流组织措施进行考虑，并未将各个技术站的车站的改编能力、技术站之间区段的通过能力考虑在内。在目前我国的实际生产中，部分地区的站、线通过能力依然存在局部紧张的情况[14]，而车流运动集结法可以极大减轻车站的改编能力。因此，以列车运行图定能力为约束，将超出图定的车流，采用技术站间车流运动集结法组织方式。技术站间车流运动集结法组织方式示意图如图2所示。

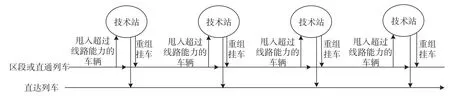
图2技术站间车流运动集结法组织方式示意图Fig.2 Schematic diagram of traffic flow organization mode of “Traffic flow motion aggregation method” between technical stations

按照单个技术站车流运动集结法组织后，如发生超出图定的货流，则采用技术站间车流运动集结法组织方式进行处理：超出车流的来源为第一类车辆(本技术站)的，留下最新近到达技术站的车流等待集结；超出车流的来源为第二类车辆(替换达到满重满轴条件)，可以考虑将其替换为第一类车辆，以方便换挂作业，然后留下最新近到达技术站的车流等待集结；超出车流来源为第二类车辆(到达该技术站)的，不能被第一类车辆替换的，则将其甩入技术站等待集结。

2 基于节约时间模型方法的技术站车流组织优化

为探讨技术站车流组织优化方法对运输时效性集结时间的最优取值，以单个车辆在技术站之间运输所花费的时间最少为目标建立计算模型。按单方向考虑，设A1，A2，…，An，分别为同一径路上的n个技术站，所有车辆均在该径路运送；各技术站每隔t小时就会从自己所在区段产生各种去向的车辆。设从Ai站去往Aj站的车辆表示为Aij，第k个t小时从i站产生去往j站的车辆数为fk(i，j)，其中，k为某一个t小时的编号，i= 1，2，…，n，j= 1，2，…，n。

设技术站相邻车站之间的距离分别需机车xi·t小时走行；所有技术站无调中转时间为w·t小时，则有调中转时间为(w+ 1 +y)t，w为无调中转时间系数；则换挂车组(优化方法下)相比无调中转进入技术站多余作业时间平均为y·t；y为t的倍数，表示换挂中转系数。

设m为一列车的平均编成辆数，q为车流运动集结法达到满重满轴条件时进入技术站“运动集结”的次数，表示运动满重满轴条件系数。设一列车集结到满重满轴条件时需要p·t小时，其中p为t小时内产生车辆数fk(i，j)的倍数，表示等待满重满轴条件系数。则列车集结时间T集可表示为

式中：p为等待满重满轴条件系数；t为技术站集结时间，h；m为列车平均编成辆数，辆。

而在现有集结参数理论中，列车集结时间T集可表示为

式中：c为集结参数，其影响因素为集结中断和车组配合到达程度；m为列车平均编成辆数，辆。

通过作差计算可知，技术站车流组织优化方法节约的单位货车时间可以表示为

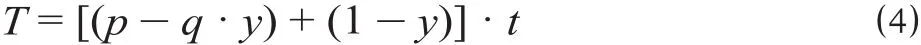
由于公式 ⑷ 中，y，p，q分别为外界客观值，唯有集结时间t是一个人为规定的主观变量，因而能决定节约时间的惟一参数即是集结时间t，将系数p和q换为现有的集结参数c。

由于货车在运动集结的过程中，货车总数不变，因而等待满重满轴条件系数p与运动满重满轴条件系数q在数值上是比较接近的，即各个技术站间的集结参数差异较小；考虑到此种情况可令q等于p，得到公式 ⑸。

结合公式 ⑵、公式 ⑶、公式 ⑸，可得车流运动集结法所得节约时间计算模型为

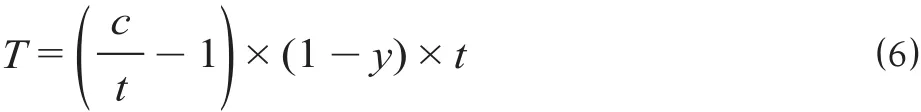
根据车站各项作业时间标准[11]，估算可知换挂货物列车相比无调中转列车进入技术站多余作业时间为50 min，即y·t为0.83 h。根据我国技术站的集结参数c通常为8 ~ 10 h[11]，取车10 h，将数据带入公式 ⑹ 可得节约集结时间变化趋势图如图3所示。

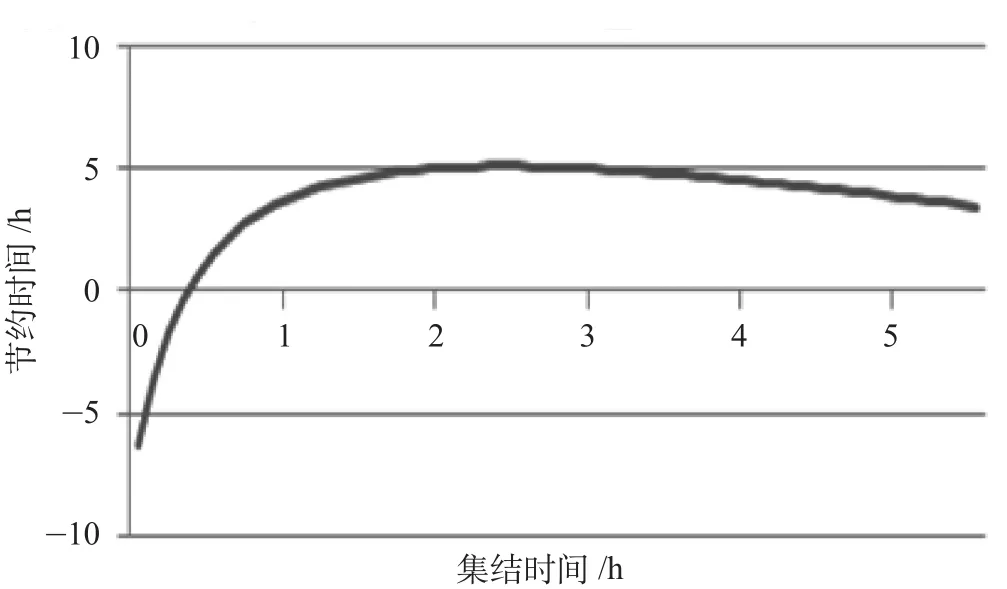
图3 节约集结时间变化趋势图Fig.3 Trend map of saving aggregation time

由公式 ⑹ 计算可得，当集结时间t取2.9的时候，车流运动集结法应用较为充分，节约时间较多为5.067 h。

当T＜ 0时，即在某些极端情况下，各技术站间的集结参数发生特别大的差异时，即q≫p，车流运动集结法不能节约时间，尤其随着我国经济社会转型发展，技术站将逐渐减少组织技术直达的情况，表明各个技术站的技术直达列车的组织条件极易容易满足，而不需要采用车流运动集结法来节约集结时间。因此，在我国现有的铁路运输供需矛盾下，车流运动集结法可以普遍提高列车运输时效性。

3 结束语

由于铁路运输的特点及其原有的运输组织方式，时效性低下一直是铁路货运的短板。车流运动集结法在未提高列车运输成本的情况下，不但节约了货车运输时间，而且提高了货车运达时间的准确性，集结时间t的确定，迫使滞留在技术站的货车在运输途中寻求集结，避免了一些车辆在一个或者几个技术站等待集结很长时间的情况，从而将货车运输时间确定在一个较小的变化范围内，在一定程度上克服了目前铁路列车集结时间较长的缺陷，对铁路运输吸引时效性较强的货物，实现“货运增量”发展具有重要意义。由于车流运动集结法运行的条件依赖于完备的列车追送统计处理系统，还需要进一步研究强大的数据处理功能作为支撑。