嵌入SMA丝的复合材料轴的刚度与变形特性研究

张晓梅,赵仰生,任勇生,赵 奇

(1.山西煤炭职业技术学院,太原 030031;2.山东科技大学 机械电子工程学院,山东 青岛 266590)

复合材料的比强度、比刚度和阻尼比传统金属材料要高,这不仅可以减轻重量,同时还能减少结构的振动,因而在飞机、船舶等对承载重量要求苛刻的领域内轴的设计中,具有广阔的应用前景。

但由于纤维复合材料力学性能的各向异性,在复合材料轴的轴向拉伸、横向弯曲以及扭转之间存在明显的耦合。

形状记忆合金(shape memory alloy-SMA)是一类应用广泛的智能材料。利用温度诱发SMA马氏体相变以改善复合材料板和梁结构的刚度特性和变形特性的研究,已经获得了一些重要的进展[1]。然而,将SMA埋入普通纤维复合材料轴,研究SMA马氏体相变对复合材料轴的刚度特性和变形特性的影响,是一个全新的尝试,迄今为止,国内外相关研究的报道还很少见到[2-3]。

Sawhney和Jain[2]制备一个埋入SMA丝的纤维增强复合材料轴并且对其进行了实验研究。在理论研究方面, Baz和Chen[3]基于有限元数值方法分析了具有SMA丝的复合材料实心驱动轴的静力学和温度效应。研究发现,当SMA丝发生温度诱发马氏体相变时,轴的扭转刚度可以得到明显的提高。但是我们也注意到,在上述研究中,有关回复应力等描述SMA丝特性的重要力学参数主要出自一些有限的实验数据,此外,在力学建模过程中仅限于实心轴而不涉及空心复合材料轴的情形。

本文针对具有简支边界的复合材料薄壁轴,进行静力学建模与变形特性分析。基于变分渐进法(Variational Asymptotic Method-VAM)[4]描述复合材料薄壁轴的截面特性。在建模过程中,基于文献[4]位移和应变的表达式,进一步引入了剪切变形的影响。基于虚功原理推导出复合材料薄壁轴的偏微分静平衡方程组。采用Galerkin法计算和分析了薄壁复合材料薄壁轴的变形特性。通过数值计算揭示了SMA丝的含量、初始应变、温度、铺层角以及旋转速度对复合材料轴等效抗弯刚度的和静变形特性的影响。

1 静力平衡方程的建立

长度为L埋入SMA纤维的复合材料薄壁轴如图1所示。为了对其进行力学分析与建模,采用惯性坐标系(x,y,z)和局部坐标系(x,s,ξ),假定环向坐标s正方向为薄壁轴中面切线逆时针方向,径向坐标ξ正方向为薄壁轴中面法线方向。

图1 圆截面复合材料薄壁轴Fig.1 Composite thin-walled shaft of a circular cross section

将文献[4]的建模思想做进一步扩展,在计入横向剪切变形的情况下,假定薄壁轴横截面任意一点沿着x,y,z方向的位移,取如下形式

u1(x,y,z)=U1(x)-y(s)θy(x)-z(s)θz(x)+g(s,x)

u2(x,y,z)=U2(x)-zφ(x)

u3(x,y,z)=U3(x)+yφ(x)

(1)

式中,U1(x),U2(x),U3(x)分别为横截面沿x,y,z轴刚体位移;φ(x),θy(x),θz(x)分别为横截面绕x,y和z轴的扭转角。注意方程(1)中的y,z表示横截面中心围线上的点的坐标,是环向坐标s的函数。

假定薄壁轴的翘曲函数g(s,x)具有如下形式:

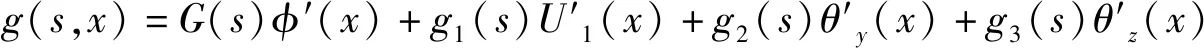
(2)

方程(2)右端表达式中的四项分别表示扭转、拉伸、绕z和y轴弯曲的翘曲分量,其中,G(s)表示扭转率,g1(s)表示轴向应变,g2(s)和g3(s)分别表示沿y,z轴的弯曲曲率。

在方程(1)、(2)中,θy(x),θz(x)可以表示为:

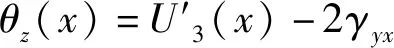
(3)

按照文献[4],根据位移方程(1)和(2)能够得到横截面正应变γxx和面内剪应变γxs,进一步按照文献[5],将横向剪应变γxξ的形式进行修改,可以写出考虑横向剪切的薄壁轴的几何方程:

2γxξ=

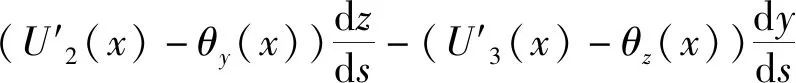
(4)

定义薄壳力:

(5)

薄壳力和应变本构关系:

Nxξ=D(s)γxξ,

(6)

其中

(7)

复合材料传动轴的静力平衡方程利用变分原理导出:

δU+δw=0

(8)

其中,δU和δw分别为应变能的变分和虚功。应变能U分别由两部分组成,其中,由于复合材料轴变形产生的应变能:

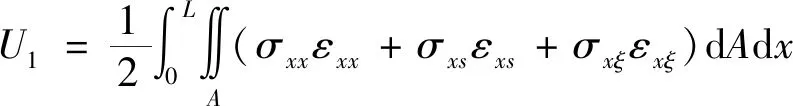
(9)

其中,σxx,σxs,σxξ分别表示横截面正应力、面内剪应力和横向剪应力,εxx,εxs,εxξ是相应的工程应变。

另一方面,由于SMA丝回复力NSMA和温度力NΔT产生的应变能[3]:

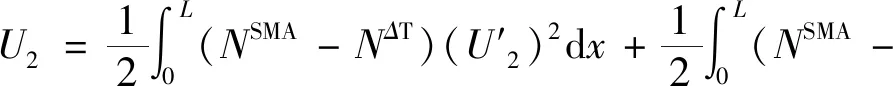
(10)

于是,总应变能表示为:

U=U1+U2

(11)

虚功δw包括外载荷的虚功和旋转惯性力的虚功,其中外载荷的虚功:

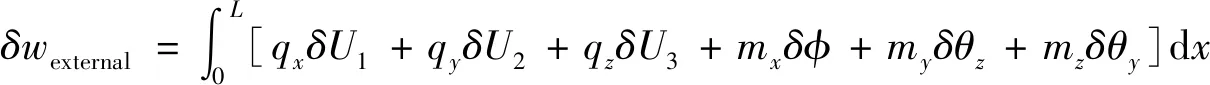
(12)

其中,qx,qy,qz分别表示沿x,y,z方向的分布力;mx,mz,my分别表示关于x,y,z轴的分布力偶矩。

惯性力的虚功为:

(13)

所以,虚功表示如下:

δw=δwexternal+δwinertial

(14)

变形应变能的变分为:

(15)

其中:

(16)

将式(6)代入式(16),并且利用几何方程(4),可得:

(17)

其中,kij(i,j=1,…,6)是复合材料薄壁轴横截面的刚度系数,表达式如下:

(18)

通过将表达式(18)与文献[4]进行对比,发现36个刚度系数kij(i,j=1,…,6)中,只有16个刚度系数kij(i,j=1,2,…,4)与文献[4]不考虑剪切变形复合材料薄壁轴的刚度系数一致,剩下的20个刚度系数kij,(i=1,2,…,6;j=5,6),kji(i=1,2,…,4;j=5,6)是由于考虑剪切变形而新增加。

将δU和δw代入变分原理(8),在周向均匀刚度配置(Circumferentially Uniform Stiffness-CUS)下, 导出弯-剪耦合静力方程如下:

(19)

式中,qy=qy0Δ(x-xl),qz=qz0Δ(x-xl)分别是已知的沿y、z轴横向剪力;my=my0Δ(x-xl),mz=mz0Δ(x-xl)分别是已知的绕y、z轴的弯矩。Δ(x-xl)代表狄拉克函数,xl表示力(力矩)作用点的位置。

2 方程求解

假定弯曲位移U2(x),U3(x)和转角θy(x),θz(x)具有下列形式:

(20)

其中,取满足两端简支轴位移边界条件的近似函数为:

(21)

U2j,U3j,Θyj,Θzj是待定系数。

将式(20)代入方程组式(19),采用Galerkin法,得:

[KΩ+K1]{X}={F}

(22)

其中:

(23)

(24)

{F}T=(AiBiCiDi)

(25)

(26)

在此,广义位移XT定义为

XT={U2j,U3j,Θyj,Θzj}1×4N, (j=1,2…,N)

(27)

在式(19)和式(22)中,NSMA和NΔT表示SMA丝产生的沿轴线方向的受限回复应力的合力以及轴向温度载荷,分别计算如下:

(zk-zk-1)ΔT]

(28)

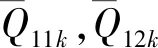
3 数值结果与讨论

针对含SMA丝的石墨/环氧型复合材料轴,进行变形特性分析,其几何尺寸为:截面半径r=0.127 m,长度L=2.023 m,厚度h=0.381 mm,铺层方式为[θ,-θ,θ,-θ,θ,-θ]。复合材料的性能参数如表1所示,SMA的材料参数如表2所示。轴的跨中受到沿z轴方向的集中载荷qz0=2 000 N的作用。

表1 复合材料性能参数Tab.1 Mechanical properties of composite material

表2 SMA的材料参数Tab.2 Material properties of SMA wires[9]

通过对复合材料轴在旋转时的变形特性分析,可以获得SMA丝的含量和初始应变、纤维铺设角和转速等参数对等效抗弯刚度和变形的影响规律。图2和图3表示复合材料轴跨中的等效刚度随铺层角的变化曲线,同时也给出了SMA丝的含量以及初始应变的影响。复合材料轴跨中的等效抗弯刚度基于该点铅垂集中载荷与铅垂位移之比来计算。结果表明,复合材料轴的等效抗弯刚度随着SMA含量以及初始应变的增加而增加。此外,从图中还可以看出,当铺层角在15°附近时的等效抗弯刚度取得最大值。

图4和5表示温度的改变对复合材料轴跨中的等效抗弯刚度的影响,其中也分别展示出SMA丝的含量以及初始应变的影响。温度变化从0 ℃上升到100 ℃(M→A),然后在从100 ℃下降到0 ℃(A→M).从图4和5中可以看出,复合材料轴跨中的等效抗弯刚度随温度的变化曲线是典型的迟滞迴线。在一个热循环周期内,等效抗弯刚度随温度的变化可以分为两个阶段:增加阶段和减少阶段;在马氏体向奥氏体相变的过程中,等效抗弯刚度随着温度的增加而增加,而从奥氏体向马氏体相变的过程,等效抗弯刚度随着温度的减小而下降;从图4可以发现,随着SMA丝含量的增加,等效抗弯刚度也随之提高,迟滞迴线向上发生整体迁移;从图5可以看出,与SMA丝含量的影响不同,在升、降温阶段的某些温度区间,不同初始应变下的迟滞迴线会相互重叠在一起。

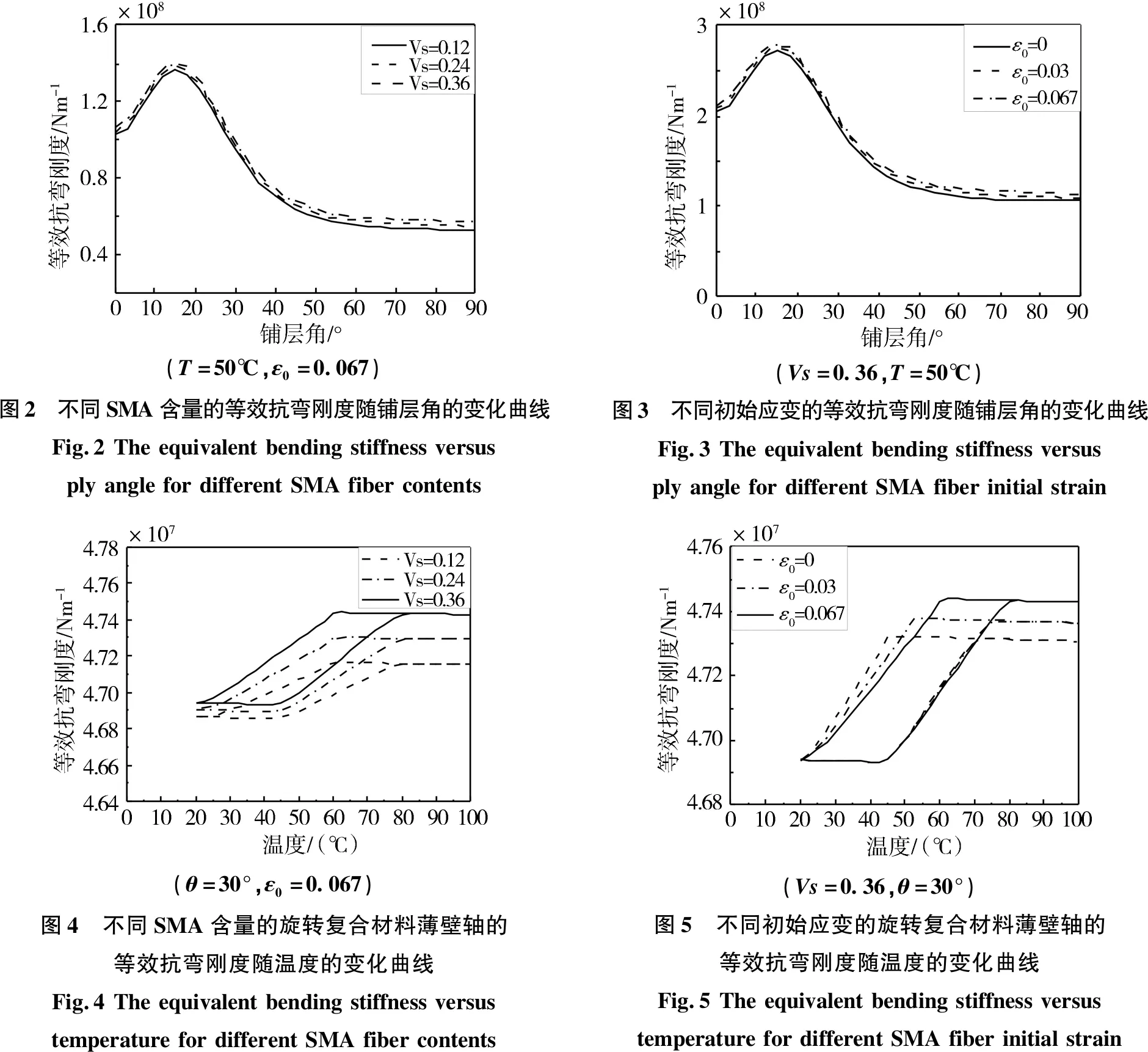
(T=50℃,ε0=0.067)图2 不同SMA含量的等效抗弯刚度随铺层角的变化曲线Fig.2TheequivalentbendingstiffnessversusplyanglefordifferentSMAfibercontents(Vs=0.36,T=50℃)图3 不同初始应变的等效抗弯刚度随铺层角的变化曲线Fig.3TheequivalentbendingstiffnessversusplyanglefordifferentSMAfiberinitialstrain(θ=30°,ε0=0.067)图4 不同SMA含量的旋转复合材料薄壁轴的等效抗弯刚度随温度的变化曲线Fig.4TheequivalentbendingstiffnessversustemperaturefordifferentSMAfibercontents(Vs=0.36,θ=30°)图5 不同初始应变的旋转复合材料薄壁轴的等效抗弯刚度随温度的变化曲线Fig.5TheequivalentbendingstiffnessversustemperaturefordifferentSMAfiberinitialstrain

图6和7表示复合材料轴跨中的铅垂集中载荷作用下的挠度曲线,其中给也出了SMA丝的含量以及初始应变的影响。由图6可见,增加SMA丝的含量可以明显提高复合材料轴抗弯刚度,从而减少轴的弯曲变形;而SMA丝的初始应变似乎对轴的弯曲变形没有明显的影响。

图8表示转速对复合材料轴的弯曲静变形的影响。结果表明,转速对轴的影响主要体现在软化效应,即,复合材料轴抗弯刚度随着转速的增加而减小,所以,导致相应的弯曲变形随着转速的增加而增加。

图9表示具有不同纤维铺设角的复合材料轴的弯曲变形曲线。结果表明,适当选择纤维铺设角,有助于降低复合材料轴的弯曲变形。

(T=50℃,ε0=0.067,Ω=1000rpm,θ=30°)图6 不同SMA含量的旋转复合材料薄壁轴的横截面铅垂位移曲线Fig.6TheverticaldisplacementofcrosssectionfordifferentSMAfibercontents(Vs=0.36,T=50℃,Ω=1000rpm,θ=30°)图7 不同初始应变的旋转复合材料薄壁轴的横截面铅垂位移曲线Fig.7TheverticaldisplacementofcrosssectionfordifferentSMAfiberinitialstrain(T=50℃,Vs=0.36,θ=300,ε0=0.067)图8 不同转速的旋转复合材料薄壁轴的横截面铅垂位移变化曲线Fig.8Theverticaldisplacementofcrosssectionfordifferentspinspeed(Vs=0.36,T=50℃,ε0=0.067,Ω=1000rpm)图9 不同铺层角的旋转复合材料薄壁轴的横截面铅垂位移变化曲线Fig.9Theverticaldisplacementofcrosssectionfordifferentplyangle

图10和11分别表示具有不同的SMA丝的含量以及初始应变的复合材料轴的横截面绕y轴转角曲线。有此可见,SMA丝的含量以及初始应变对复合材料轴的横截面转角没有明显的影响。这可能是由于SMA丝沿着复合材料轴的轴向单向铺设所造成的。

图12和13分别表示转速和铺层角对复合材料轴的横截面转角曲线的影响,由此可以看到,转速和铺设角对复合材料轴的横截面转角的影响,类似于它们对弯曲变形的影响(见图8和9)。

图14-17表示复合材料轴跨中的铅垂位移-温度变化曲线,其中分别展示了SMA丝含量、初始应变、转速和纤维铺设角的影响。由于弯曲变形与抗弯刚度成反比,所以,图14-17中所有的位移-温度迟滞迴线的方位与图3和4的刚度-温度迟滞迴线的方位刚好相反。由图14和15可以看到,SMA丝含量和初始应变对位移-温度迟滞迴线的影响与它们对刚度-温度迟滞迴线的影响是相似的。图16和17表明,转速和纤维铺设角能够明显地改变位移-温度迟滞迴线的大小,这也就意味着上述参数对复合材料轴的弯曲变形随温度的变化程度的大小有显著的影响。

(T=50℃,ε0=0.067,Ω=1000rpm,θ=30°)图10 不同SMA含量的旋转复合材料薄壁轴的横截面绕y轴转角变化曲线Fig.10Rotationsangleofcrosssectionabouty-axiswithdifferentSMAfibercontents(Vs=0.36,T=50℃,Ω=1000rpm,θ=30°)图11 不同初始应变的旋转复合材料薄壁轴的横截面绕y轴转角变化曲线Fig.11Rotationsanglecrosssectionaroundy-axiswithdifferentSMAfiberinitialstrain(T=50℃,Vs=0.36,θ=300,ε0=0.067)图12 不同转速的旋转复合材料薄壁轴的横截面绕y轴转角变化曲线Fig.12Rotationsangleofcrosssectionaroundyaxiswithdifferentspinspeed(Vs=0.36,ε0=0.067,Ω=1000rpm)图13 不同铺层角的旋转复合材料薄壁轴的横截面绕y轴转角变化曲线Fig.13Rotationsangleofcrosssectionaroundyaxiswithdifferentplyangle(ε0=0.067,Ω=1000rpm,θ=30°)图14 不同SMA含量的旋转复合材料薄壁轴跨中铅垂位移随温度变化曲线Fig.14Theverticaldisplacementofthemiddleofshaftvs.temperaturewithdifferentSMAfibercontents(Vs=0.36,Ω=1000rpm,θ=30°)图15 不同初始应变的旋转复合材料薄壁轴跨中铅垂位移随温度变化曲线Fig.15Theverticaldisplacementofthemiddleofshaftvs.temperaturewithdifferentSMAfiberinitialstrain

为提高计算精度,同时验证计算结果随式(20)截取项数N增加的收敛性,在位移表达式(20)中,取不同项数计算复合材料轴跨中铅垂位移并进行比较,结果如表3所示。由表3可知,随着项数N的增大,铅垂位移趋于一个固定值,说明本文提出的模型与算法具有收敛性。

(Vs=0.36,θ=300,ε0=0.067)图16 不同转速的旋转复合材料薄壁轴跨中铅垂位移随温度变化曲线Fig.16Theverticaldisplacementofthemiddleofshaftvs.temperaturewithdifferentspinspeed(Vs=0.36,ε0=0.067,Ω=1000rpm)图17 不同铺层角的旋转复合材料薄壁轴跨中铅垂位移随温度变化曲线Fig.17Theverticaldisplacementofthemiddleofshaftvs.temperaturewithdifferentplyangle

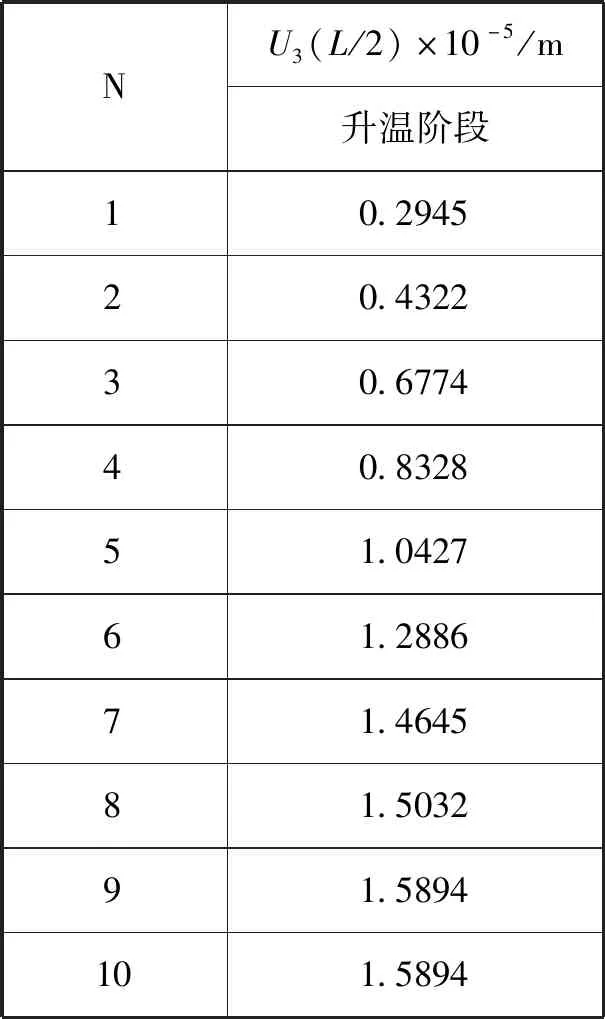
表3 Galerkin法的收敛性(轴跨中铅垂位移随N变化趋势)Tab.3 Convergence of Galerkin method (variation of vertical displacement of the middle of shaft with N).

4 结论

研究了一个埋入SMA丝的复合材料轴的刚度和静变形特性。基于复合材料薄壁梁理论、Brinson热力学本构方程和变分原理建立轴的静力平衡方程,采用Galerkin法进行模型离散化和近似求解。分析结果表明:

(1)利用SMA丝的马氏体相变驱动作用可以显著改善轴的等效抗弯刚度特性和静变形特性;

(2)温度的变化对轴的静力学特性有重要的影响,在一个热循环周期内,由于马氏体向奥氏体相变(M→A)以及逆相变(A→M)的发生,等效等效抗弯刚度以及横向弯曲变形随温度的变化曲线是典型的迟滞迴线;

(3)SMA丝含量和初始应变的增加,可以提高轴的等效抗弯刚度,减小弯曲变形;另一方面,纤维铺设角和转速可以明显改变位移-温度迟滞迴线的大小,例如,当铺层角在15°附近时的等效抗弯刚度可以取得最大值,而复合材料轴抗弯刚度随着转速的增加而减小,说明这些参数能够对复合材料轴的变形随温度变化程度有显著的调节作用。本文的分析结果对于埋入SMA丝的复合材料传动轴的刚度和变形特性的提供了一定的理论依据和参考价值。