基于线性规划模型的城轨列车运行图调整策略
何占元,阴佳腾,王明主
(1.朔黄铁路发展有限责任公司,河北 肃宁 062350;2.北京交通大学 轨道交通控制与安全国家重点实验室,北京 100044;3.北京交通大学 电子信息工程学院,北京 100044)
在过去,城市轨道交通的客运需求相对现在而言较小,城轨列车之间的追踪间隔较大,这种情况下学者们普遍认为城市轨道交通由于线路网络结构单一、列车运行交路固定、列车运行速度较低,在本质上属于一种简化的干线铁路,可以将干线铁路的列车实时调度方法直接用于城市轨道交通的列车实时调度调整,因此过去的列车调度研究主要针对于干线铁路或高速铁路[1][2],专门针对城市轨道交通列车调度调整的文献研究相对较少。近年来,随着城市规模扩大、人口增多,城市轨道交通迅速发展,城市轨道交通系统呈现了网络化、大客流以及高密度运行的趋势,从列车延误产生原因、延误传播规律和调整方法上讲,都已经与传统的干线(或高速)铁路产生了很大的差异。因此近年来很多国内外学者开始关注城市轨道交通的列车行车调度和调整问题[3]。
从延误产生原因上讲,当前城市轨道交通中列车运行延误主要由设备故障(线路设备、信号设备、供电设备和车辆设备等)、人为原因(如司机误操作、突发大客流、乘客跳下站台等)和其他突发故障(如极端天气、火灾、恐怖袭击等)三类构成。总体上来说,设备和人为故障占到了日常运营管理中的绝大部分,约占到90%以上,设备和人为原因占的比率与每条地铁线路的实际运营情况和设备可靠度有关。比如,伦敦地铁没有加装屏蔽门(Platform Screen Doors, PSD)系统,因此经常出现人为原因(如乘客随身物品落入轨道)导致列车突发停车产生延误;北京地铁2号线于2017年上半年刚刚加装屏蔽门系统,试运行期间系统可靠性相对较差,出现多起屏蔽门故障而导致的列车延误情况。
城市轨道交通系统中存车线是辅助线的一种,主要用于备用列车、故障列车的存放。合理使用存车线的备车能为运营组织创造方便、灵活的调整手段[4]。现有几乎所有的轨道交通线路,包括北京地铁、上海地铁等,都在线路中设计了若干条存车线。如图1所示,在城市轨道交通线路中存车线可以设置于两个车站之间的运行区间内,在存车线中可以存放一辆备车,如果线路中出现严重故障导致列车运行间隔不均时,可以通过加开备车的方式弥补线上运能的不足,尽快疏散站台滞留乘客。通常情况下,备车可以根据不同的线路布局通过多种路径(Route)进入正线。“跳停”则指的是列车在经过站台时组织列车以不停站的方式通过站台(也称越站),通常用于故障消除后,列车为恢复至正常运行图而进行的“赶点”运行,跳停对于恢复至初始运行图非常有效。实际中,结合以上两种调度方式,在遇到突发故障或列车延误时,能够迅速得到并及时实施最优的列车调度方案,以降低故障或运行延误对乘客的服务质量造成的影响,并能尽快使轨道交通系统恢复至正常的运营秩序与性能指标。
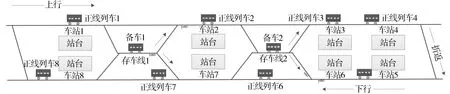
图1 考虑存车线的轨道交通线路拓扑结构示意图Fig.1 A schematic diagram of the topological structure of rail transit lines considering car storage lines
本文在以上背景下建立基于混合整数线性规划(Mixed integer linear programming, MILP)的数学模型,结合“跳停”和“加开备车”两种常用的行车调度手段,用以优化故障场景下的列车运行图调整方案,以提高线路的故障恢复能力,尽快疏散因线路故障而滞留的乘客。
1 问题描述
本文中我们用KE={1,2,…ke}表示正线运行的列车集合;KA={1,2,…ka}表示存车线备车的集合;KF={1,2,…kf}表示故障后从车辆段发车、进入正线运营的列车集合。在故障结束、线路恢复运行时,本章所考虑问题就是对正线列车、存车线备车和车辆段列车的运行计划重新进行调整,通过跳停的策略使线路快速恢复至正常运行秩序(如图2所示)。
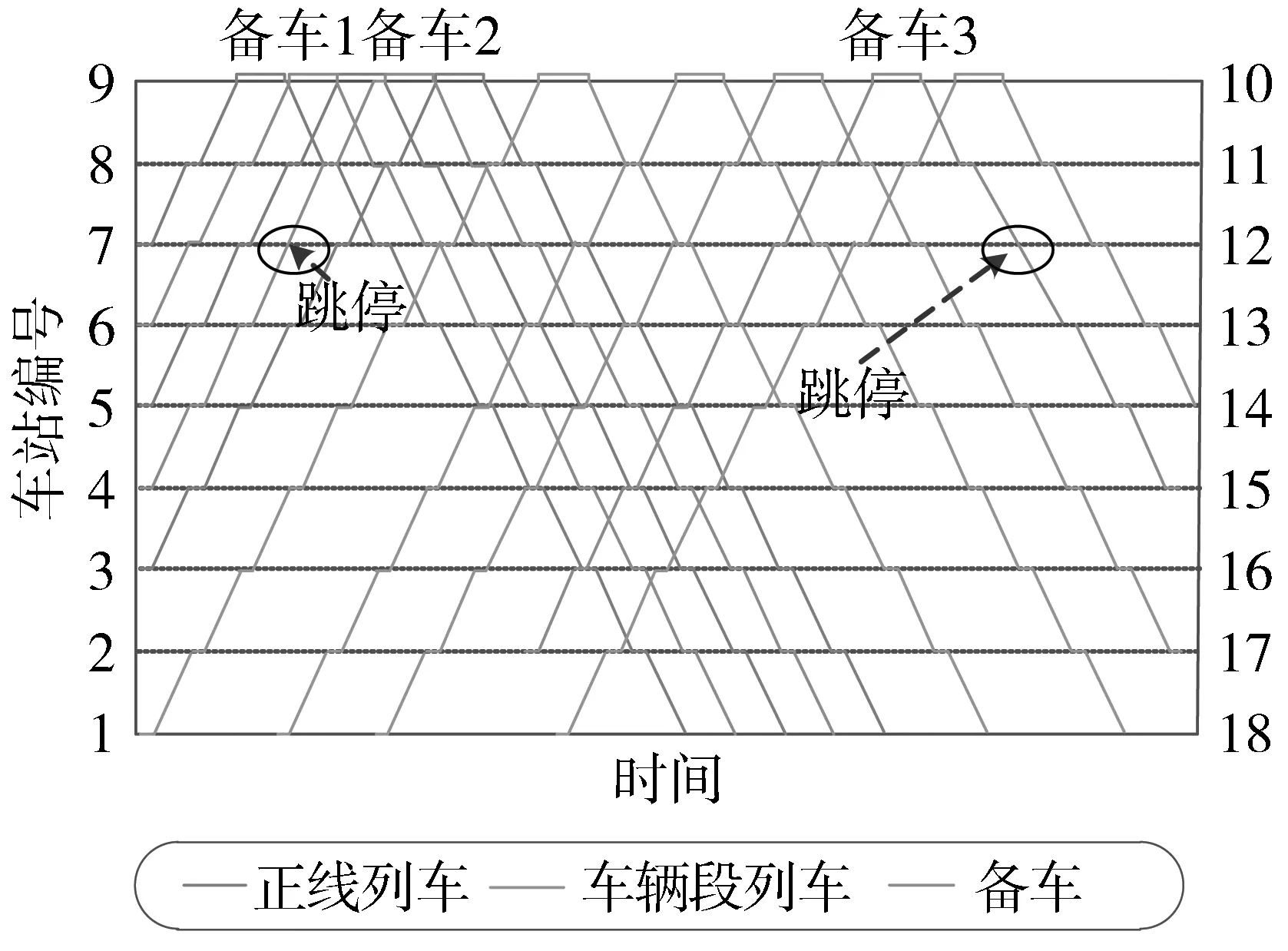
图2 考虑跳停和加开备车的列车运行图调整Fig.2 Train rescheduling based on stop-skipping and backup trains
1.1 本文基本假设
根据城市轨道交通系统的实际运营特点,本文研究的模型和方法主要基于以下假设:
假设1:列车运行调整过程中可以采用“跳停”策略,即在某些车站直接通过不停车。跳停策略能够在一定程度上缓解站台客流拥堵情况、降低乘客平均等待时间。
假设2:轨道交通线路设计了若干条存车线,并且存车线中事先存储了备车可用于应急情况下的列车运行调整。实际中运营公司可以根据体育赛事或节假日等预测客流信息,在运营前的天窗期将备车置于存车线。
1.2 符号和变量表示
为方便对考虑问题的建模,表1中统一列出了本文使用的参数和符号的定义。
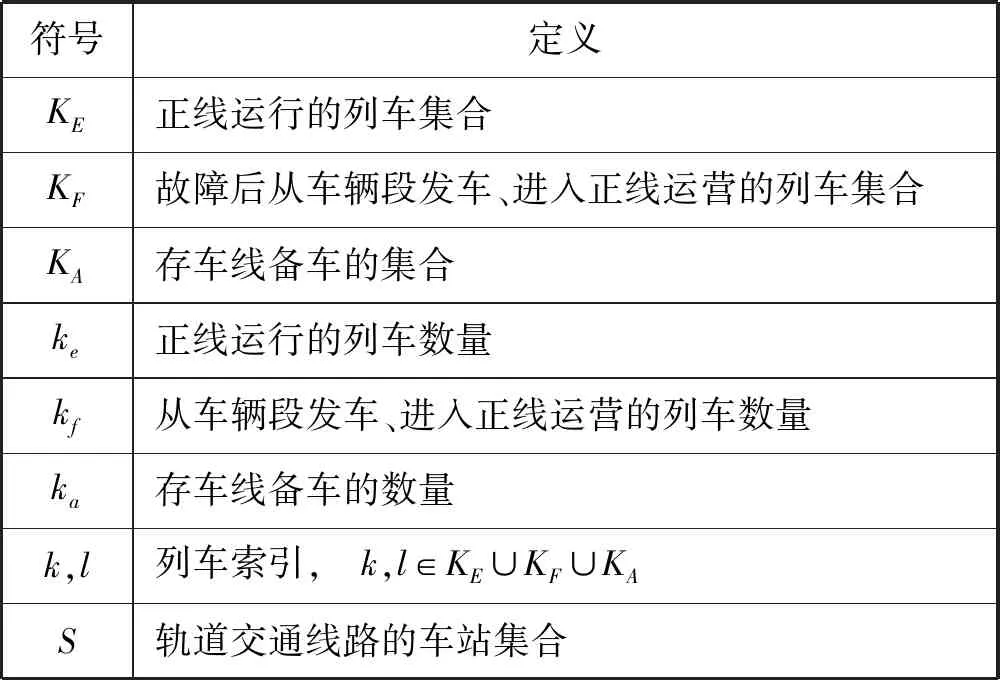
表1 本文使用的符号和定义Tab.1 The symbols and definitions
续表1
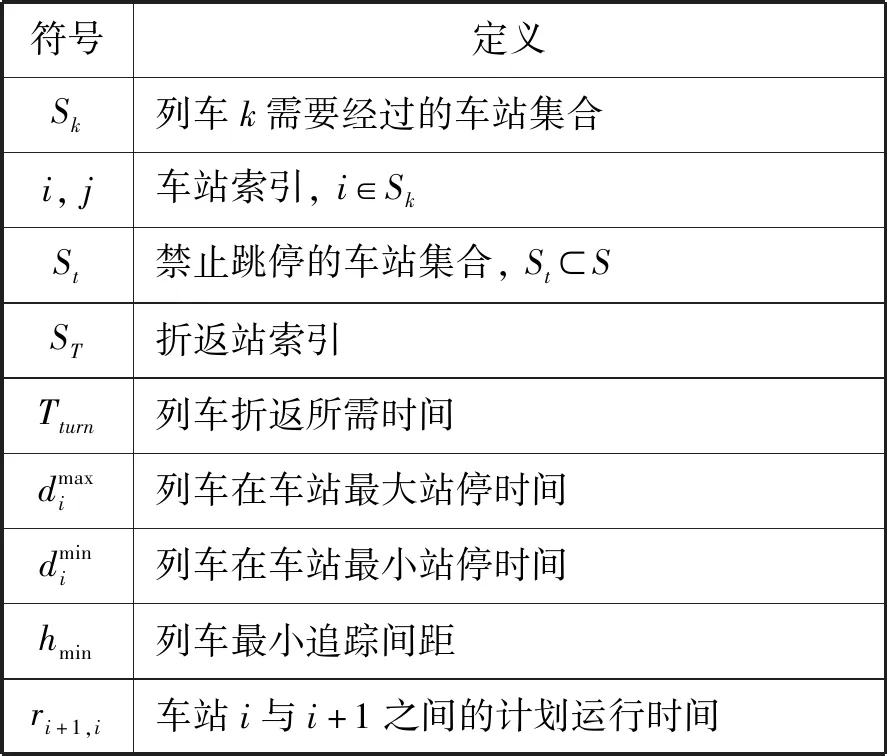
符号定义Sk列车k需要经过的车站集合i,j车站索引,i∈SkSt禁止跳停的车站集合,St⊂SST折返站索引Tturn列车折返所需时间dmaxi列车在车站最大站停时间dmini列车在车站最小站停时间hmin列车最小追踪间距ri+1,i车站i与i+1之间的计划运行时间
本文的决策变量包括以下几部分:
nk,i列车k是否在i站跳停(0-1变量)。对于任意k∈KE∪KF∪KA,i∈SSt,如果列车在i站跳停,则nk,i=1;否则nk,i=0
xk,i列车k到达车站i的时间(整数变量)
yk,i列车k离开车站i的时间(整数变量)
zk,l列车运行次序(0-1变量)。对于任意l∈KA,k∈KE∪KF,如果列车k先于列车l, 则zk,l=1;否则zk,l=0
pk,l列车运行次序(0-1变量)。对任意k,l∈KA,如列车k先于列车l, 则pk,l=1; 否则pk,l=0.
首先我们以图1为例来解释数学模型中的符号和变量定义。图1中的轨道交通线路包括八个车站,可得|S|=8表示车站集合中的元素数量为8. 线路中有两个存车线,分别位于车站1和2、车站6和7之间。为了便于理解,这里我们假设车站3的供电系统出现故障导致列车无法发车、后续车辆无法进入车站。故障于t0时刻结束,车站3恢复发车能力。此时由于列车延误导致车站中大量乘客滞留,因此需要启用存车线中的备车来尽快恢复线路运力。本文中我们考虑了三种列车类型:第一种是正线运行列车(即集合KE),这些列车在故障结束时于正线运行,如正线列车1、正线列车2;第二种是存车线的备车(即集合KA),如图1所示的备车1和备车2可以从侧线分别驶入车站2和车站6;第三种列车在故障结束后从车辆段发车、进入正线运营(即集合KF)。在本文考虑的列车运行调整问题中,正线列车和备车按照既有路径从当前车站开始运行,因此对于每一辆列车k我们定义集合Sk表示列车将要运行的路径。比如,图1中的正线列车2对应集合Sk={2,3,4,5,6,7,8},表示正线列车2将依次经过车站2,3,4…,8;备车2对应Sk={7,8},表示备车2将依次经过车站7和车站8。假设计划运行图所规定的列车运行次序为K={e1,e2,…,f1,f2,…}, 在列车运行调整过程加入备车a1和a2后,备车位置不同会产生多种可行的列车运行次序,例如K={e1,a1,e2,…,f1,f2,a2,…}或者K={e1,e2,a1,…,f1,f2,a2,…}等等。因此,在使用备车的情况下如何优化列车之间的运行次序也是本文解决的问题。为此我们定义变量zk,l表示正线列车与备车之间的次序;并且定义pk,l表示备车之间的先后次序,以这种方式可以将所有列车的运行次序完备地表示出来。
1.3 模型约束
下面介绍数学模型的基本约束,包括列车运行时分约束、站停时分约束、运行间隔约束、折返约束和运行次序约束等。
约束一:运行时分约束
xk,i+1-yk,i≤ri+1,i,∀k∈KE∪KF∪KA,i,i+1∈Sk
(1)
其中ri+1,i表示列车在车站i+1与车站i之间的最短运行时分,对应列车在区间使用最大速度曲线得到的运行时分。
约束二:列车跳停与站停约束

(2)
∀k∈KE∪KF∪KAi∈Sk
(3)
yk,i-xk,i≤M×(1-nk,i)
∀k∈KE∪KF∪KAi∈Sk
(4)

约束三:列车运行间隔约束
列车运行间隔约束用来确保列车的运行间隔在一个合适的范围,从而避免前后列车相撞或ATP紧急制动。在正常情况下列车的发车次序不变,可以分别定义前后两两列车之间的安全间隔。本文由于考虑了三种类型列车,列车之间的运行次序可能发生改变,因此我们将列车运行分为如下四种情况分别定义其运行间隔约束:
(1)正线列车运行间隔约束
yk+1,i-yk,i≥hmin∀k∈KE∪KF,i∈Sk
(5)
xk+1,i-xk,i≥hmin∀k∈KE∪KF,i∈Sk
(6)
由于本文不考虑列车的越行,因此正线列车和车辆段列车的次序保证不变。以上两组约束定义了正线列车和车辆段的列车按照计划运行图保证运行间隔。
(2)正线列车与备车之间的运行间隔约束
如果zk,l=1,则模型中加入下面的约束:
∀i∈Sl,k,k+1∈KE∪KF,l∈KA
(7)
以上约束表示,由zk,l=1可知备车l的次序是在列车k和k+1之间。因此式(7)确保备车列车l与列车k和k+1之间保持一定的运行间隔。
(3)备车与备车之间的运行间隔约束
如果pk,l=1,则模型中加入下面的约束:
yl,i-yk,i≥hmin∀i∈Sl∪Sk,k,l∈KA
(8)
以上约束表示备车k和备车l之间也需要满足运行间隔约束。
约束四:列车运行次序约束
下面一组约束规定了是否在调整中使用备车。如果调度员希望使用所有存车线中的备车,则对于每辆备车l∈KA定义如下约束。
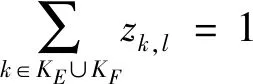
(9)
此外,决策变量pk,l也需要满足一定的约束,来保证备车之间合理的运行次序。
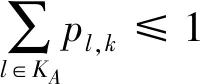
(10)
(11)
pk,l=0 ∀k,l∈KA,k=l
(12)
公式(9)表示,每一辆备车k至多只有一辆备车l追踪;公式(12)表示,对于一辆列车k自身,其运行次序变量pk,l=0.
图3给出了一个简单的例子用于直观地说明以上的约束。该例子中考虑了三辆备车、三辆正线运营列车以及四辆车辆段列车。从运行图中可以看出,三辆备车分别于正线列车1、正线列车2和车辆段列车3之后发车,根据这种运行次序可知变量zke1,1=1,zke2,2=1,zkf3,3=1, 其中ke1,ke2,kf3分别表示正线列车1、正线列车2和车辆段列车3。此外,根据三辆备车的运行次序我们也可以得到p1,2=1以及p2,3=1.
约束五:列车折返约束
yk,i+1-yk,i=Tturn
∀k∈KE∪KF∪KA,i=ST
(13)
列车折返约束限制了列车在折返站的折返时间。
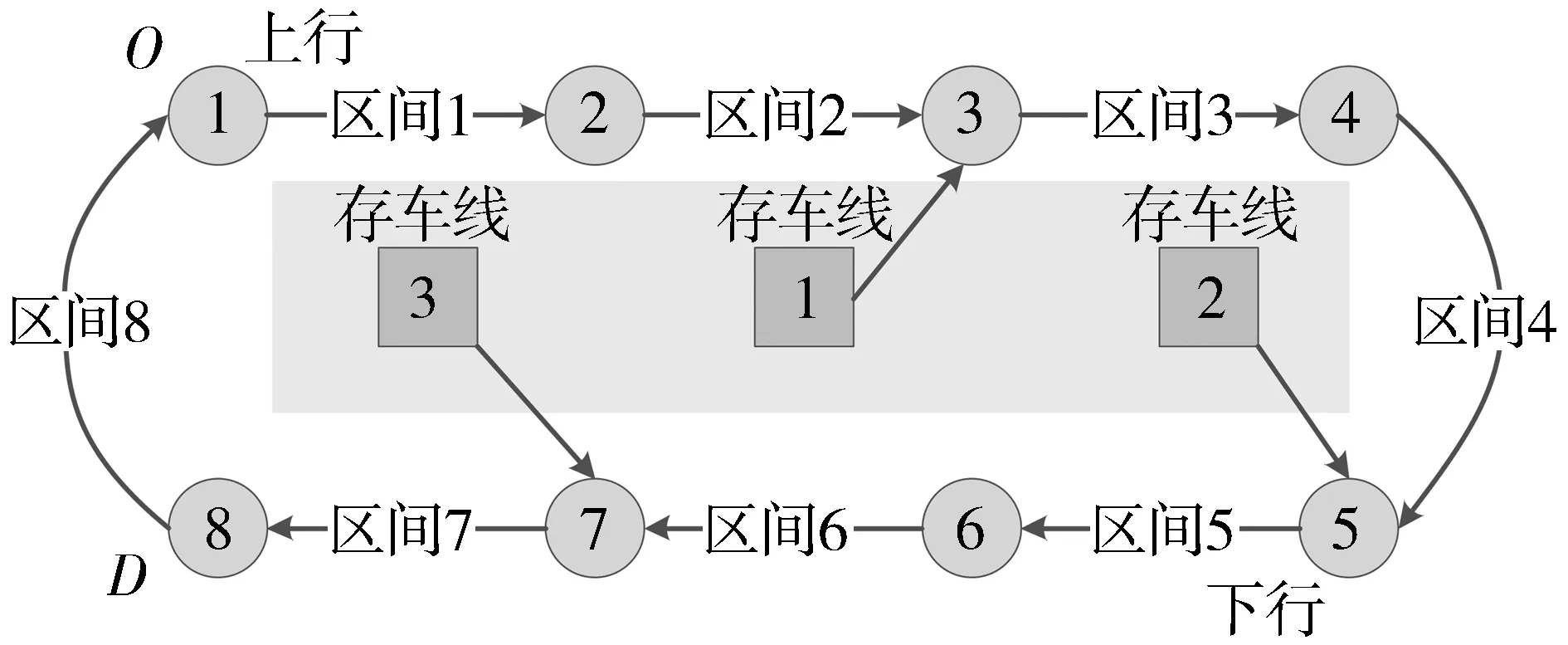
图3 考虑存车线的双向轨道交通运行线Fig.3 Bi-directional rail transitline based on car storage line
1.4 模型目标函数构建
接下来考虑构建模型的目标函数。本文所考虑的基本问题是故障修复、线路恢复正常运营时间段,此时行车调度的主要目的是尽快疏散站台滞留的乘客,维持正常的列车运行秩序。在考虑备车的情况下,本文的主要优化目标是尽可能保证列车运行安全的情况下提高线路运力、增大发车频次。因此本文将列车到达终点站的时间总和设置为目标函数。目标函数定义如下:
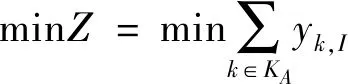
(14)
s.t., 公式(1)-(13)
xk,i∈Z+,yk,i∈Z+,nk,i∈{0, 1},
pk,l∈{0,1},zk,l∈{0, 1}
2 仿真算例
本文的算例使用VC++编码,并在CPU为i7-5600U-2.60Ghz的Windows 8上运行。此外,本文使用分支定界法求解模型(14),分支定界算法在软件IBM ILGO CPLEX 12.3 Academic Version上实现。本文算例的线路拓扑结构如图3所示,我们规定仅有备车可以在调整过程中实施跳停决策,并且每辆列车至多在一个车站进行跳停。
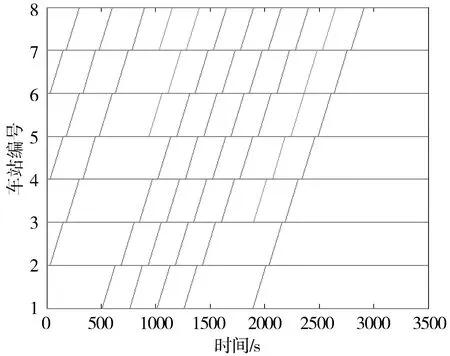
图4 考虑跳停和加开备车情况下的优化列车运行图调整方案Fig.4 Optimized train diagram adjustment scheme based on stop-skipping and backup trains
本算例给出了本文所构建模型和算法的求解结果,并给出了11辆列车在最小运行间隔为200 s情况下的最优列车运行图以及跳停方案。图4显示了使用三辆备车的列车运行图。从中可以看出,该运行图满足了列车运行间隔,所有列车都按照一定的间隔有序运行。另外可以看出,三辆备车采取了不同的跳停策略:第一辆和第二辆备车由于离终点站较近,没有采取跳停决策;而最后一辆备车在车站6采取了跳停决策。通过这样的优化调整使线路的列车运行密度更高,能够更好地缓解故障导致的线路客流负荷。
3 结论
列车运行调整是城市轨道交通日常运营管理中需要掌握的关键技术之一。本文从应急条件下的列车运行调整出发,提出了一种考虑跳停和加开备车策略的城轨列车运行图调整方法,通过结合多种行车调度策略使线路尽快恢复行车秩序,保障应急条件下的线路运力。将列车运行过程转化为相应的状态约束,构建了混合整数线性规划模型(Mixed-integer linear programming),并使用分支定界和CPLEX优化软件进行求解。最后设计仿真实验验证了本文方法的有效性。
随着城市轨道交通系统复杂性、网络性的提高,调度中心如何实现大量信息的集成和快速处理是今后急需解决的核心问题,也是今后全自动运行系统的发展趋势。今后的列车运行调整研究将更趋向于结合多种调整手段,从一体化的角度实现系统性能的最优,为乘客提供更高质量的服务水平[5]。

