基于MapReduce的并行加权k近邻与离群检测
郭娟娟,赵旭俊,张继福
(太原科技大学 计算机科学与技术学院,太原 030024)
k近邻查询是最简单的机器学习算法之一,用于多维空间中查询与给定对象最近的k个对象[1],其广泛应用于数据挖掘及地理信息系统等多个领域[2]。同时k近邻查询也存在一些问题:传统方法在查询k近邻时,视所有属性对查询结果同等重要,但是在实际应用场景中,不同属性对查询结果的影响是不同的,若忽略不同属性的差异,将产生大量无意义的近邻数据;并且随着数据量的增大,传统k近邻查询方法处理效率低,不能满足大数据时代下人们对算法性能的要求。
MapReduce是由Google公司提出的一种具有可扩展和高容错的并行编程模型[3],它将数据进行分割并分布到多个工作节点上,利用集群数据节点之间的并行性,分别处理这些数据,然后执行归约操作,形成最终结果。
本文结合大数据的应用背景,给出一种基于MapReduce的并行加权k近邻查询与离群检测算法WKNNOM-MR,主要贡献如下:(1)充分考虑分布式计算的因素,紧密结合MapReduce计算框架,提出适合分布式实现的加权k近邻查询方法,并在Hadoop平台上实现该方法;(2)全面衡量每个对象与其加权k近邻的关系,提出一种新的离群挖掘方法;(3)为了避免发生数据倾斜现象,采用LSH划分策略,分散数据,使得各节点的工作量大致平衡;(4)最后在具有5个节点的Hadoop集群上实现该算法,并采用人工合成数据集、UCI标准数据集进行实验,结果验证了该算法的有效性、可扩展性和可伸缩性。
1 相关工作
1.1 加权k近邻查询的并行化实现
k近邻查询是指根据相似性度量在数据集中查询与给定对象最近的k个数据对象,其中Indyk和Motwani[4]提出使用局部敏感哈希LSH查找k近邻,通过哈希函数构建哈希桶,将相近的对象以较高的概率映射到相同的桶中,从而在每个桶中找各自的最近邻。但是随着大数据时代的到来,传统的方法已不能满足现实需求,算法的性能也有待进一步提升,从而加快了分布式数据计算的发展。Qing He等[5]提出基于KD-Tree进行k近邻查询的并行离群数据挖掘算法,并采用MapReduce框架实现,取得了较好的挖掘效果。Stupar等[6]提出使用Map Reduce框架解决海量高维数据的近似k近邻集查询问题,将LSH技术应用于第一个MapReduce阶段,实现合理的分区映射,有效提高了k近邻的查询效率。同时,传统的方法忽略了不同属性对查询结果的影响,视所有属性是同等重要的,因此,本文提出一种适合分布式实现的加权k近邻方法,用于解决海量数据集的加权k近邻查询问题。
1.2 离群检测算法的并行化实现
离群挖掘是用来发现数据集中实际存在、但又容易被忽略的有价值数据,传统的离群检测方法[7-8]易受维度影响,不适合用于高维数据挖掘,因此将高维数据映射到低维空间后再进行相似性度量是个可行的方法。文献[7-9]提出利用MapReduce计算模型实现并行离群点检测算法,通过迭代计算来更新全局候选离群点,找出离群度最大的数据点,但是该算法需要使用多个MapReduce,耗时较多。因此苟杰等[10]提出只需要一次MapReduce的并行化算法PODKNN,首先对数据集进行无损划分,之后在Map阶段查询k近邻并计算离群因子,在Reduce阶段进行汇总归约,确定离群因子大的对象为离群对象。杨海峰等[11]利用MapReduce编程模型,实现了一种上下文离群数据并行挖掘算法,并用实验验证了该算法的可解释性和有效性。张继福等[12]在Hadoop平台上,提出了一种基于MapReduce和相关子空间的局部离群数据挖掘方法,利用局部稀疏差异度矩阵确定相关子空间,在其相关子空间中计算数据的离群因子,有效降低了“维灾”对离群挖掘的影响,实验证明该算法具有较好的挖掘效果及可扩展性和可伸缩性。
综上所述,多数k近邻查询方法是建立在所有属性的重要性相同的基础之上,假设数据的所有属性是同等重要的,但是在很多实际应用中,各个属性对近邻查询的重要程度是不同的;同时,随着数据量与数据维度的不断增大,现有的很多离群检测算法性能较差,不能很好的解决实际应用中所遇到的困难。因此,本文将针对以上问题展开研究。
2 基于Z-order的加权k近邻与离群检测算法
2.1 基于Z-order的加权k近邻
Z-order曲线是空间填充曲线的一种,能将高维空间数据映射到低维空间,有效降低维度对结果的影响。该曲线穿过且仅穿过一次高维空间中的每一个离散网格,依据穿过的顺序为这些网格进行统一编号,该编号称为Z-value值,简称Z值。Z-order曲线就是由数据集DS中的对象,经位交叉计算得到Z值,再将所有Z值相连形成的Z形曲线,具体的1阶、2阶Z-order曲线如图1所示,其中阶数代表了空间被划分的程度,阶数越大,空间被划分的越细。
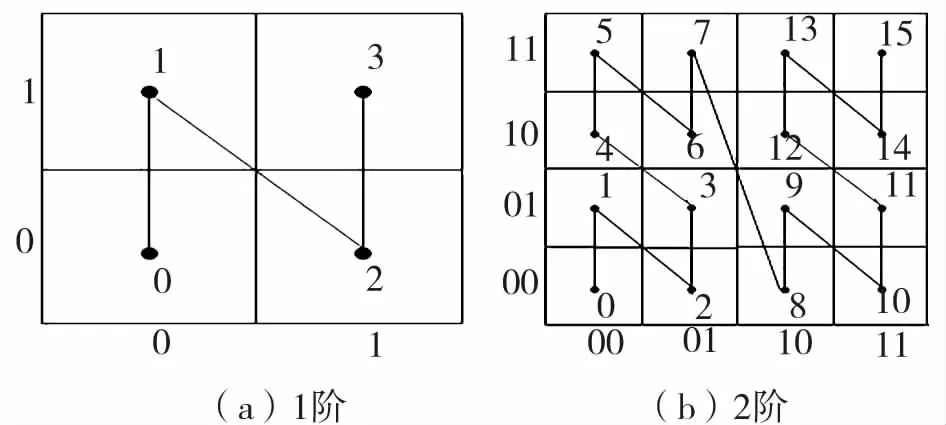
图1 Z-order曲线
Fig.1 Z-order curve
Ramaswamy和kyuseok等人[13]提出使用k近邻方法处理实际问题,但其没有考虑不同属性重要程度对结果的影响,为解决这一问题,提出加权k近邻,为不同属性赋予不同权值,充分考虑属性的重要程度对结果的影响。而信息熵是一种很好的度量权重的方法,用平均信息量体现信源各个离散消息的不确定性,有效地刻画了信息的量化度量问题[14]。参照文献[14],相关概念和定义描述如下:
定义1:给定数据集DS,A={A1,A2,...,Ad}是DS的属性集,每个属性有n个值Ai={Ai1,Ai2,...,Ain},Ail的信号量为I(Ail)=-log2Pl,Pl表示Ail出现的概率,信源的信息熵即:
(1)
在本文中,H(Al)值越大,属性Al的重要程度越高,该属性的信息量就越多。信息熵从平均意义上表征了属性Al的总体特征,因此对所有属性的信息熵进行归一化操作,从而确定各个属性的权值。令属性权值为W(A)={w1,w2,…,wd},其中:
(2)
采用Z-order曲线进行加权k近邻查询时,存在高维空间中相近的对象映射到低维空间中不相邻的情况,为了避免这种现象发生,引入加权k近邻候选集与随机位移操作的概念。
定义2:给定数据集DS,O={O1,O2,...,On}是DS的对象集,Z'是对象Oi的Z值,在对所有Z值排序之后,生成一个有序数列,Z值小于Z'的k个对象为Oi的前驱,大于Z'的k个对象为Oi的后继,由Oi的前驱和后继组成的集合,称为Oi的加权k近邻候选集,记为C(Oi).
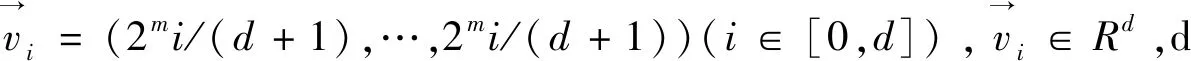
采用Z-order曲线搜索加权k近邻的详细步骤如下:(1)根据信息熵计算原始数据集DS中每个属性的权值,对原始数据集赋权之后得到加权数据集DS';(2)将加权后的属性值进行二进制编码,并采用文献[15]中方法,对DS'中所有对象的二进制属性值进行位交叉操作,得到各自的Z值;(3)按照Z值的大小对数据集进行重新排序,在排序结果中,找到每个对象的k个前驱和k个后继,从而确定所有对象的加权k近邻候选集;(4)为了保证查询结果的准确性,根据定义3对DS'进行随机位移操作,生成f个随机位移副本,每个副本都重复执行步骤2和3,DS'中的所有对象都会产生拥有2kf个元素的加权k近邻候选集;(5)计算每个对象与其所有加权k近邻候选集中元素的欧式距离,距离最小的前k个即为该对象的加权k近邻。
2.2 基于加权k近邻的离群检测算法
采用k近邻查询方法进行离群检测时,需要考虑查询对象与其k个最近邻的关系,目前已有的离群检测方法要么只考虑数据对象与其k个近邻的整体水平,要么只考虑与第k个近邻的关系,而本文采用综合分析的方法,既考虑整体水平,也考虑数据对象之间的个体差异。
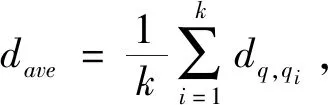
(3)
dq是查询对象q的离群因子,本文定义前TOP-N个dq值最大的点为离群点。
3 基于MapReduce的加权k近邻与离群检测
MapReduce是Hadoop平台上处理大数据集的编程框架,能够运行在成千上万个普通机器的节点上,具有很高的容错性。k近邻查询是根据相似性度量在数据集中查询与给定对象最近的k个数据对象。加权k近邻是在传统k近邻的基础上,对不同属性赋予不同权值,用于区分各属性的重要程度。因此,可以借助MapReduce编程框架,将大数据集切分为独立的小块,在每个小块中进行加权k近邻查询,进一步得到对象的离群因子,从而确定数据集中的离群对象。本文提出的基于MapReduce的并行加权k近邻与离群检测算法实现过程如图2所示。
3.1 数据预处理
随着信息社会的发展,数据量不断增大,在考虑数据属性重要程度时,需要对大量数据进行扫描,从而计算出权值,但此过程非常耗时,开销很大,因此,对数据集进行抽样,从而用样本数据集的属性权值代替整个数据集的属性权值。本文使用文献[16]的采样方法,对大数据集中数据随机均匀采样,并通过实验证明采样比例在1%~2%之间最佳。得到样本数据集之后,根据公式(1)、(2)确定各个属性的权值,并将结果保存到文件Weighted中,上传至HDFS,以便在第一个MapReduce中对数据加权时调用。
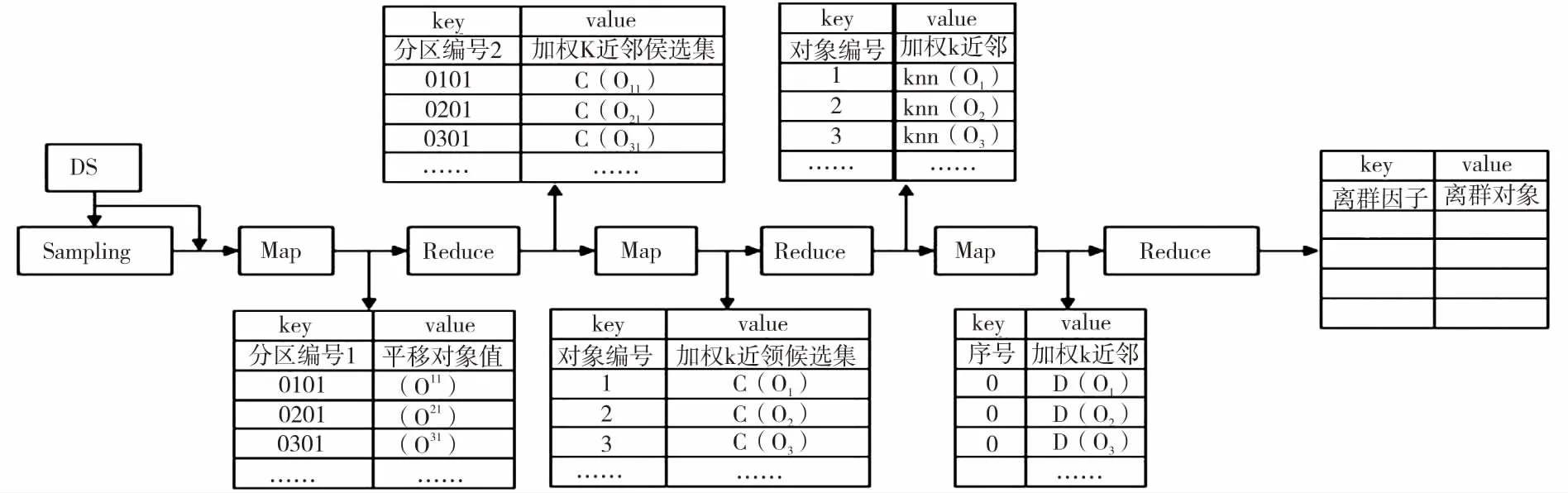
图2 MapReduce的实现过程
Fig.2 Implementation framework of MapReduce
3.2 构建加权k近邻候选集

算法1:构造数据集副本中所有对象的加权k近邻候选集
输入:数据集DS;
输出:加权k近邻候选集;
1)function MAP(key 偏移量, value 数据集DS);
2)for each O in DS ;
3)读取HDFS上的Weighted文件,根据文件中的属性权值为数据对象加权;
5)g(O)=
6)a=(a1,a2,…,anum);
7)for (i = 0;i < f;i++){
10)emit(分区编号1,平移对象值);
11)}
12)end function
13)function REDUCE(key 分区编号1, values平移对象集)
14)for (i = 0;i < n1;i++) {
15)对每个对象属性值的二进制编码执行位交叉操作;
16)位交叉的结果转为十进制即为该对象的Z值;
17)}
18)for (j = 0;j < n1;j++) {
19)查询比q'的Z值小的k个对象放入Z-中,比q'的Z值大的k个对象放入Z+中;
20)将Z-、Z+插入到加权k近邻候选集中;
21)emit(分区编号2, 加权k近邻候选集);
22)}
23)end function
3.3 确定加权k近邻
第二个MapReduce读取第一个MapReduce的输出文件,根据每个对象与其加权k近邻候选集中所有对象的距离确定最终的加权k近邻,具体实现如算法2所示。在Map阶段,以键值对< key 偏移量,value 加权k近邻>作为输入,分割每条读入数据,以
算法2:计算对象的加权k近邻
输入:第一个MapReduce的输出
输出:加权k近邻
1)function MAP(key 偏移量, value 加权k近邻候选集)
2)对读入的数据进行切分;
3)emit(对象编号, 加权k近邻候选集);
4)end function
5)function REDUCE(key 对象编号, values加权k近邻候选集)
6)for (i = 0;i < 2kf;i++){
7)for (j = 0;j < d;j++){
8)disq=sqrt(disq+(qj-pij)2);
9)}
10)}
11)找到disq最小的k个对象为对象q的加权k近邻;
12)emit(对象编号, 加权k近邻);
13)end function
3.4 确定离群数据
第三个MapReduce读入第二个MapReduce的输出文件,根据每个对象与其加权k近邻之间的距离计算离群因子,确定前TOP-N个离群因子最大的对象为离群对象,具体实现如算法3所示。在Map阶段,以键值对
算法3:计算离群因子,确定离群对象
输入:第二个MapReduce的输出
输出:前TOP-N个离群对象
1)function MAP(key 偏移量, value 加权k近邻)
2)for (i = 0;i < k;i++) {
3)for (j = 0;j < d;j++) {
4)disq=sqrt(disq+(qj-pij)2);
5)}
6)}
8)emit(0, 分区编号3);
9)end function
10)function REDUCE(key 0, values分区编号3)
11)for(i = 0;i < n;i++){
12)比较n个对象的dq值大小,保留最大的TOP-N个;
13)}
14)emit(离群因子, 离群对象);
15)end function
4 实验与分析
4.1 UCI标准数据集
实验环境:硬件配置为Intel(R) Core(TM) i5-4570 CPU、8G内存、Windows7操作系统的笔记本一台,在虚拟机VMware-workstation-12.0.0上安装Ubuntu14.04操作系统,分布式平台为hadoop2.6.0,集成开发环境为Eclipse,采用java语言实现伪分布环境下的WKNNOM-MR算法。
实验数据: UCI机器学习库中的数据集Anuran Calls (MFCCs),该数据集所含数据量为7 195,属性个数为22个,异常值为73个。
为了比较不同副本个数(即参数f)对算法WKNNOM-MR各项性能的影响,将副本数f设定为0、1、2、5、10和22,其中:f=0代表原始数据集DS.图3(a)显示了在同一数据集中,不同副本个数f对离群检测结果准确率的影响。当f相同k不同时,准确率随k值的增大呈上升趋势;k相同f不同时,准确率随f值的增大而增大,且准确率的提升速度越来越慢。例如f=1与f=0的副本个数差1,但准确率却变化很大,f=2与f=1的变化速度也很明显;f=5、10、22三者虽然副本数相差较多,但准确率曲线却几乎完全重合。发生这种现象主要是因为在第一个MapReduce的Map阶段,对数据集中的所有对象构建数据集副本,副本数越多,Reduce阶段的任务数越多,加权k近邻候选集越庞大,出现重复对象的个数也越多,那么准确率提高的速度就会降低,到达某个峰值后不再变化。但是,随着副本数的增加,算法执行时间也会增加,实验结果参见图3(b).
4.2 人工数据集
实验环境:由5个计算节点构成的集群,每个节点的配置为2-core CPU、2G内存、40G硬盘,操作系统为Ubuntu14.04,分布式平台为hadoop2.6.0,集成开发环境为Eclipse,编程语言为java.
实验数据:利用Microsoft Excel的随机数据生成器来创建大量的人工数据,这些数据集遵循正态分布,期望为0,方差为1.本文共创建了两组合成数据集,第一组为D1、D2、D3、D4和D5,分别包含20、40、60、80和100个属性,同时每个数据集由500 000个对象构成;第二组为S1、S2、S3、S4和S5,他们拥有50个属性,其数据对象个数分别为200 000、400 000、600 000、800 000和1 000 000.
4.2.1 维度d对算法WKNNOM-MR挖掘效率的影响
本组实验采用第一组人工数据集D1、D2、D3、D4、D5来评价WKNNOM-MR的性能,取节点个数为3、4、5,k=30,实验结果如图4所示。
图4(a)显示了集群节点不同时,数据维度对算法挖掘效率的影响。随着维度的增加,算法WKN-NOM-MR的挖掘时间逐步递增,运行效率递减,同时数据量不变的情况下,节点个数越少,算法效率越低。这是因为随着数据维度增大,每条数据的属性不断增多,那么在使用Z-order曲线进行空间映射时,Z值的计算更复杂,导致每个对象的查询时间随之增加。数据量不变的情况下,HDFS文件系统中的数据块数不变,那么节点个数越多,每个节点上的运行块数越少,整个运行时间便会成比例降低,但是在实际运行中,节点个数越多,网络传输耗时也会增加,所以下降比例略有变化。
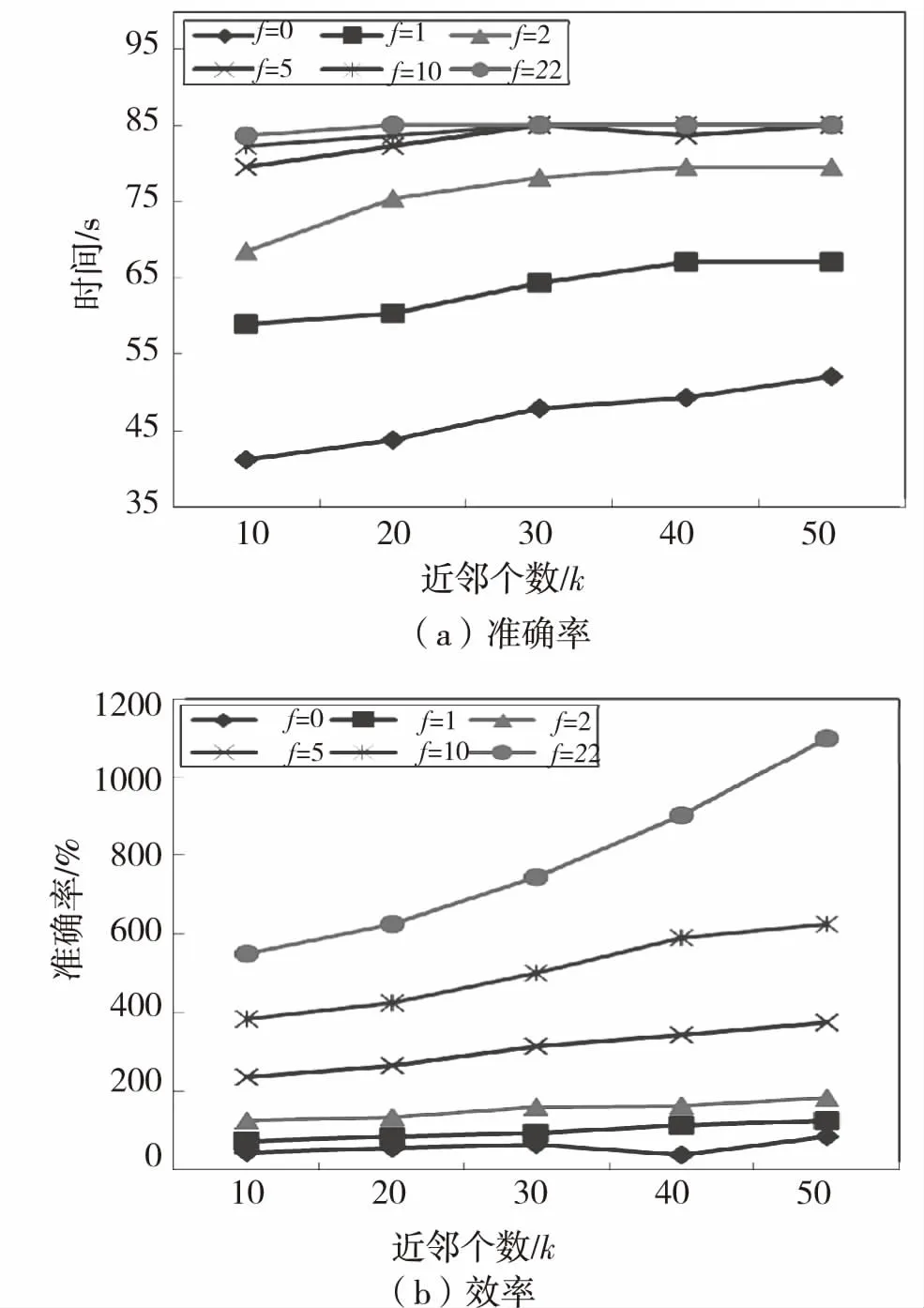
图3 副本数f的性能
Fig.3 Performance of replica numberf
为了测试WKNNOM-MR算法在维度上的可扩展性,采用时间比来定量分析。在本实验中,时间比是不同维度数据集的运行时间同20维数据集的运行时间之间的比例。通过时间比可体现随着维度的增加,算法WKNNOM-MR具有较好的扩展性,实验结果详见图4(b).
图4(b)是节点个数为3、4、5时的时间比变化图,随着维度的增加,时间比不断提高,且节点个数越多,时间比越大,曲线的倾斜角度逐渐高于线性。这是因为随着维度的增加,数据集容量不断变大,HDFS文件系统中的数据块变多,每个节点上的数据对象越多,集群的I/O耗时越多,那么在Map与Reduce之间的Shuffle代价不断增加,导致数据维度越大,时间比越大。同时,节点个数越多,网络传输耗时越多,从而时间比越大。
4.2.2 算法WKNNOM-MR的伸缩性
本组实验采用第二组人工数据集S1、S2、S3、S4、S5来评价WKNNOM-MR的伸缩性,取节点个数为3、4、5,k=30,实验结果如图5所示。
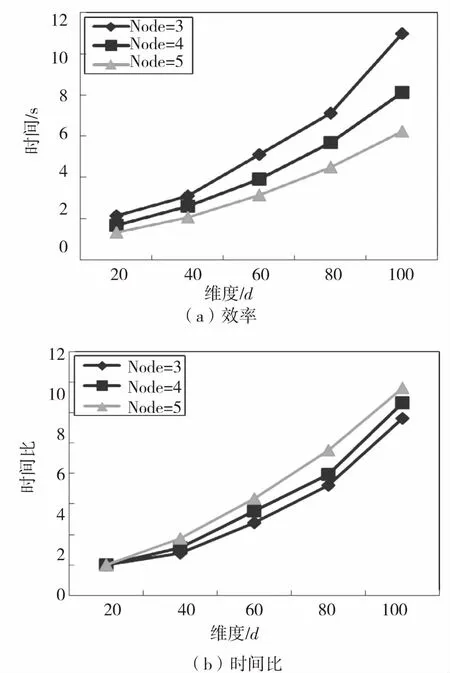
图 4 维度对挖掘效率的影响
Fig.4 Efficiency impact of dimension
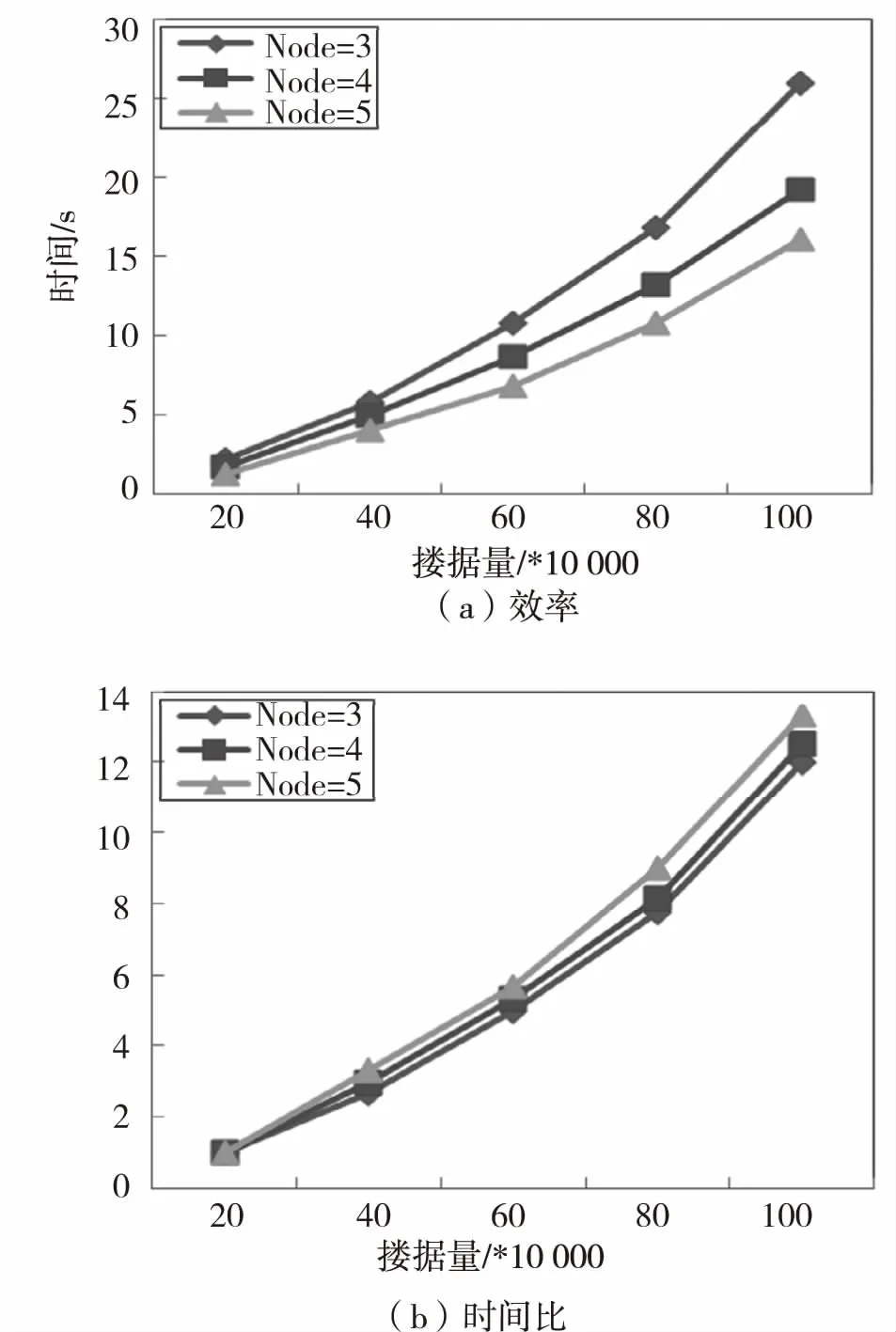
图5 数据量对挖掘效率的影响
Fig.5 Efficiency impact of data amount
图5(a)显示了节点个数不同时,数据量对WKNNOM-MR挖掘效率的影响,数据量越大,算法运行时间越长,且节点个数越多,算法的运行时间越少,效率越高。这是因为hadoop平台的任务数是由HDFS分配给节点的数据块数决定的,数据量越多,每个计算节点上分配的数据对象也越多,导致每个节点要处理的任务量越多。同时对象个数越多,第一个MapReduce阶段需要构建的数据副本越多,最后生成的加权k近邻候选集越多,导致离群对象的查找随数据量的增加而线性增长。同样数据量不变时,节点个数越少,每个节点上运行的数据对象越多,负荷越大,运行时间越长,即算法的运行时间与节点个数成反比。
在本实验中,时间比被用于分析WKNNOM-MR算法在数据量上的可扩展性,它是不同数据量的运行时间同最小数据量的运行时间的比例,其实验结果呈现在图5(b).
图5(b)是节点个数为3、4、5时的时间比变化图,数据量越大,时间比越大,且节点个数越多,时间比越大,曲线倾斜角度逐渐高于线性。这是因为随着数据量的增大,HDFS文件系统中的数据块变多,分配到各个计算节点上的数据对象也会随之增加,第一个Map阶段之后的Shuffle操作代价增大,导致整个分布式运行时间变多,时间比不断变大。同时节点个数增加,网络传输耗时增加,带来运行的额外耗时变多,造成了时间比的增加。
4.2.3 算法WKNNOM-MR的可扩展性
本组实验采用第二组人工数据集中的S1、S3和S5,数据量为200 000、600 000、1 000 000条数据,每条数据有50个属性,取k=30进行实验,实验结果如图6所示。
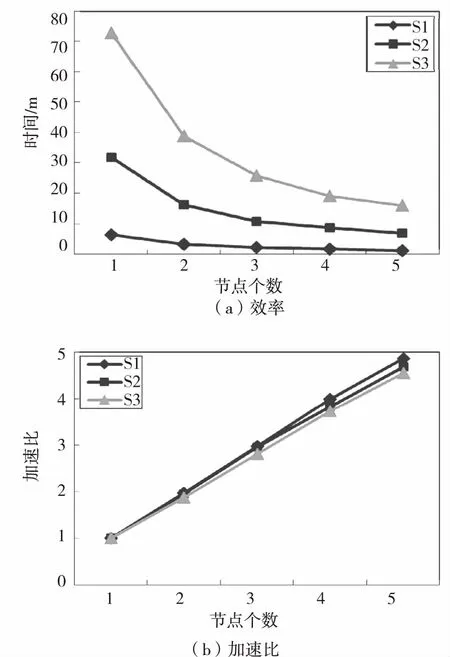
图 6 节点个数对挖掘效率的影响
Fig.6 Efficiency impact of node
图6(a)展示了不同数据集中节点个数对挖掘效率的影响,节点个数越少,数据量越大的数据集消耗的时间越多。因为算法中各个数据对象离群因子的计算完全可以实现并行化,Z值的计算不会受节点个数的影响,相应的加权k近邻候选集的构建也与节点数无关,整个计算过程的计算量只与数据对象个数成线性关系,数据对象按节点个数比例分配到各计算节点。同时随着计算节点的增加会增加一些网络传输量,Shuffle阶段受到影响,并行化的效果减弱,因此变化逐渐趋于缓慢。
为了衡量计算节点数目与算法效率之间的关系,采用加速比进行定量分析。加速比=单个计算节点上的运行时间/t个计算节点上的运行时间。在进行实验时,保持实验数据集不变,并调整计算节点的个数,得到单个节点同多个节点运行时间的比例,以此描述节点个数对算法运行时间的影响。
图6(b)是节点个数不同时,不同数据集的运行加速比变化趋势,节点个数越多,加速比越大,且数据量越少,加速比也越大,曲线整体变化趋势逐渐低于线性。因为数据量越少,HDFS文件系统中的数据块越少,每个计算节点上的数据对象越少,查询所有对象的加权k近邻所需时间也会减少,集群I/O耗时较少,这些额外耗时对加速比的影响较小,因此加速比越大。同时集群节点个数越多,算法的运行时间越短,理论上加速比应与节点数成线性关系,但在实际操作过程中,节点个数的增加带来网络传输量的增加,因此并行化的效果会逐渐降低。
5 结 论
随着信息时代的发展,数据量越来越大,离群数据的检测越来越困难。针对这一问题,本文提出了一种基于MapReduce模型的离群检测算法WKNNOM-MR.该算法是对WKNNOM的并行化设计,利用LSH数据配置策略分散数据,结合Z值计算每个对象的加权k近邻,并根据近邻距离值确定最终的离群对象。为了更好的适应海量数据的需求,下一步会在多种分布特征的数据集上及更多集群节点上进行实验分析,并将该算法用于高维数据集的离群检测。

