独柱墩桥梁上部结构抗倾覆稳定性分析

马玉荣,陈海波,吕改锋,陈恒大

(1.安徽新华学院,合肥 230088;2.江苏交科交通设计研究院有限公司,南京 210002;3.安徽建筑大学,合肥 230601;4.陕西省土地工程建设集团,西安 710075)

独柱墩连续梁桥因其空间利用率高、施工便捷度好、结构轻盈雅致等特点被广泛用在城市快速干道或高速公路匝道桥中,由于桥墩的单支承作用导致稳定性不足、抗扭能力弱,尤其是在重载交通的作用下,重车偏载倾覆问题突出[1,2]。美国AASHTO《桥梁设计规范》指出,任何结构都应有抵抗滑动、倾覆、提离或压屈的能力,而桥梁上部结构在设计中应考虑偏心荷载作用的影响,并对连续结构最小支座数量进行限制,但对支座布置形式、支座间距、支座抗疲劳性能等参数均没有提及,独柱墩桥梁在偏心荷载作用下的抗倾覆稳定性计算方法不明确。文献[3,4]模拟荷载不断增大,直至结构整体倒塌的情形,计入几何、材料双重非线性并考虑接触分析,研究了结构倾覆全过程的力学行为。日本由于地理位置的影响,对独柱墩桥梁的研究多侧重于地震方面,文献[5]对结构在地震荷载作用下的延性强度和稳定性进行了分析。

我国《公路钢筋混凝土及预应力混凝土桥涵设计规范》(2012征求意见稿)增加了采用整体式断面的连续梁桥抗倾覆计算的相关内容,但对桥梁倾覆极限状态、倾覆破坏模式、支座转动机线荷载等认识还不够深刻。文献[6]按照桥墩数量及中墩支座数量将桥梁结构分为独柱单支承、独柱双支承和双柱支承,认为独柱双支承受力状态优于独柱单支承,且桥下通透度大;文献[7]按照中墩的支承方式为铰接或者固结、上部结构为曲线梁或者直线梁进行分类,提出了支承体系差异化原则;文献[6,8]对比了独柱墩连续梁桥抗倾覆稳定性验算的支座反力法和稳定系数法,认为稳定系数法对独柱墩抗倾覆分析更加严谨。文献[9]基于能量法和力法推导出有效的曲线梁桥抗倾覆计算理论,通过对箱梁、桥墩和支座三者之间的接触分析,在不考虑支座尺寸和考虑支座尺寸两种模式下分别建立了抗倾覆计算方法,对粤赣高速匝道桥的坍塌成因进行了分析。文献[10]以三跨连续独柱墩曲线梁桥作为基本结构,不同的桥型为研究对象,建立有限元仿真模拟,基于非线性分析与接触理论,计算了三跨连续独柱墩曲线梁桥在倾覆过程中结构位移、转角及支座反力三大主要技术指标,求得了抗倾覆稳定安全系数,分析不同桥型布置下的独柱墩梁桥抗倾覆能力及倾覆力学特征,并且根据研究成果改变桥型布置参数,并完善修正了规范。文献[11]基于箱梁、支座和桥墩三者之间的相互作用关系,建立了一套实用的抗倾覆承载力计算方法,考虑了结构的几何非线性和接触非线性,建立了独柱墩梁桥抗倾覆计算的有限元模型,并与事故现场的荷载做了对比验证,认为独柱墩梁桥抗倾覆力矩包括上部结构自重和端部支座反力对转动中心的力矩,得出上部结构线重度对结构抗倾覆有显著影响。

依据文献可知,独柱墩有施工方便、结构轻巧、占地量小的优点,也有抗扭能力弱、偏心荷载作用下倾覆问题突出的不足,而国内外桥涵规范对相关内容规定比较模糊,本文以某曲线独柱墩梁桥为依托工程,分为车道荷载、车辆荷载、车队行车荷载和车队停车荷载四个加载工况,以有限元模拟为工具,求解了结构自重及二期恒载作用下以及最不利荷载作用下的桥墩各支座反力,计算了依托工程在四种工况下的箱梁抗倾覆稳定系数,为今后独柱墩桥梁的抗倾覆稳定性验算提供参考。

1 工程背景

某大桥上部结构采用44孔20 m预应力混凝土箱梁,先简支后连续,全桥共7联;下部结构采用柱式墩、钻孔灌注桩基础,桥台为桩接盖梁;桥梁第三联(13号墩-19号墩)平面位于曲线半径为272.461 m、缓和曲线为50 m的平曲线上,桥墩径向布置;下部结构采用柱式墩、钻孔灌注桩基础,其中有4个桥墩为带盖梁的独柱墩,其余桥墩为双柱墩;桥梁总宽11.4 m,桥面布置:0.25 m(护栏)+10.65 m(行车道)+0.5 m(护栏)。

上部结构采用C50混凝土、桥墩采用板式橡胶支座。恒载考虑箱梁、湿接缝及横梁的自重、10 cm沥青混凝土铺装层、8 cm混凝土现浇层和护栏等;箱梁自重按实际断面计算,混凝土容重取26 kN/m3,桥面铺装取48.2 kN/m,右侧防撞护栏单侧重取9.3 kN/m,左侧防撞护栏单侧重取4.6 kN/m.活载为车辆荷载作用,按照《公路工程技术标准》(JTG B01-2014)相关规定,取四个工况考虑按最不利车道数进行加载计算,横截面图如图1所示。

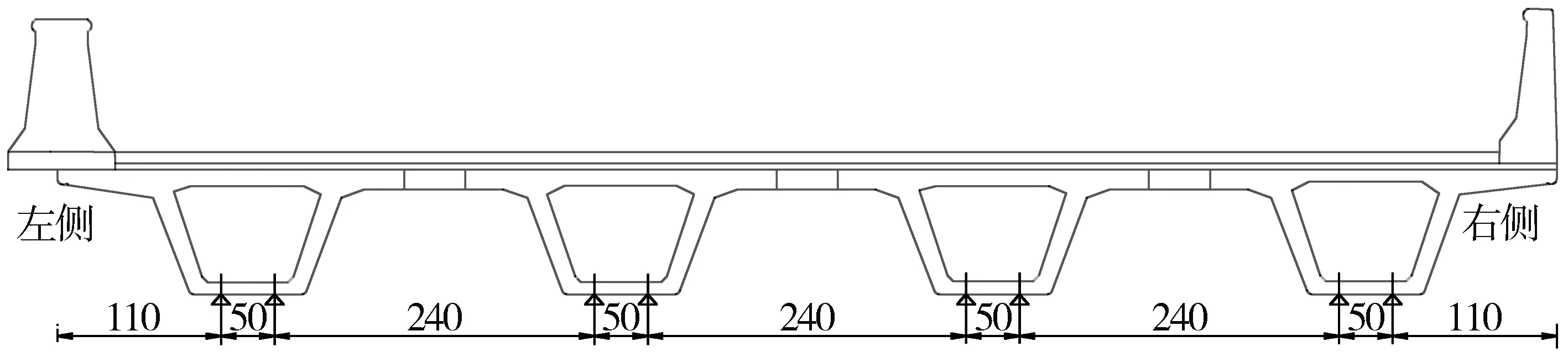
图1 上部结构横截面图Fig.1 Cross section of superstructure

2 独柱墩桥梁主要破坏形式及箱梁桥抗倾覆稳定系数公式

2.1 独柱墩桥梁主要破坏形式

独柱墩桥梁的破坏型式多样,从破坏的力学角度分析,大体可以分为4类:

(1)在偏心荷载的作用下,梁体倾覆

车辆荷载偏载,箱梁发生扭转变形,但是在支座的约束下并未发生明显变化。偏载进一步加大,甚至发生超载现象,箱梁和支座的合力作用点不断变化,逐渐向偏载一侧移动,当该作用点达到支座附近时,梁体到达倾覆临界值,继续施加偏载,箱梁倾覆发生。

此类破坏形式,支座一般不会出现较大损伤,倾覆之后梁体破损较大。

(2)扭转力矩分布不均,支座破坏

在整个桥梁中,不同的桥墩对应的支座承担的扭转力矩也不同,当有些力矩过大时,该支座被挤压变形,甚至出现偏位和破坏,导致梁体脱空,继续施加荷载,扭转力矩继续增加,没有了支座的支承作用,脱空的梁体出现脱落。

此类破坏形式,支座损伤严重,而且桥墩顶部破坏面积较大,明显超出了支座所支承的区域。

(3)支座摩阻力达到极限,梁体滑移

在荷载作用下,梁体自重及车辆荷载竖向分力为支座支承承担,但其斜向分力由支座摩阻力承担,随着荷载的增加,支座摩阻力达到极限值,再继续施加荷载,支座破坏,梁体发生侧向滑移。

此类破坏形式,支座损伤严重,梁体侧向滑移脱落,但是桥墩顶部损伤较小。

(4)桥墩偏心受压,柱体偏心破坏

在荷载作用下,桥梁倾覆过程中,桥墩受力不均匀,处于偏心受压状态。偏心受压分为大偏心和小偏心,不论大小偏心受压,都会导致墩柱局部承载能力不足,甚至是墩柱整体失稳破坏。

此类破坏形式,支座损伤较小,梁体也损伤较小,但是墩身会发生较大程度损伤,甚至是断裂。

以上四类为独柱墩桥梁破坏的主要形式,当工程实际情况不同时,受到的荷载不同,桥梁发生破坏的方式也就不同,对应的计算方法也就不同,最后采取的防治措施亦不相同。

2.2 箱梁桥抗倾覆稳定系数公式

根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62-2012)征求意见稿第4.1.9条规定,上部结构的抗倾覆稳定系数γqf计算公式如公式(1)所示:

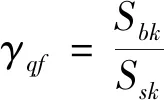
(1)

式中,Ssk为使上部结构倾覆的汽车荷载(含冲击作用)标准值;Sbk为使上部结构稳定的作用效应标准组合。

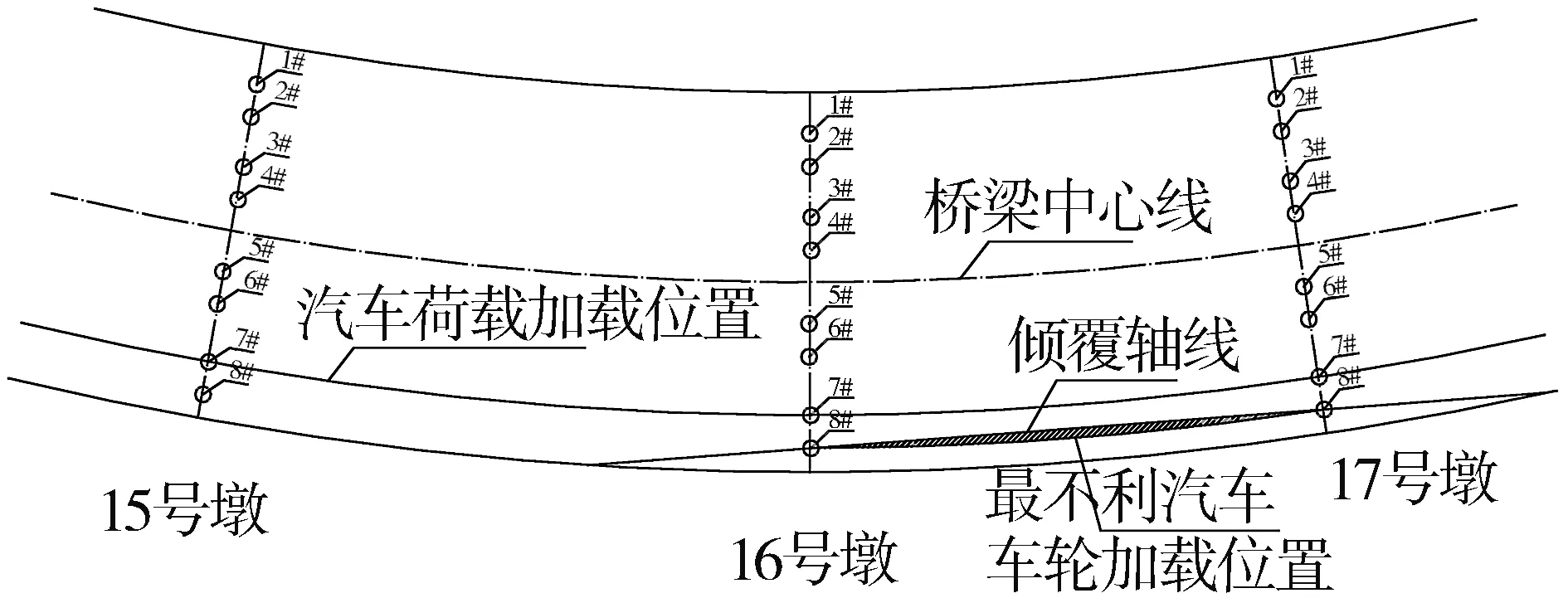
图2 车辆加载示意图Fig.2 Vehicle loading schematic

对于弯桥,当跨中桥墩全部支座位于桥台外侧支座连线内侧时,倾覆轴线为桥台外侧支座连线;当跨中桥墩全部支座位于桥台外侧支座连线外侧时,倾覆轴线取为一桥台外侧支座和跨中桥墩支座连线。如图2所示,由支座平面位置可知,本桥取最不利倾覆轴线为16号桥墩外侧支座(8#支座)和17号桥墩外侧支座(8#支座)连线,汽车荷载最不利加载位置位于桥梁倾覆轴线内侧,因此桥梁在汽车荷载作用下不会发生倾覆,为了验算结构安全性,假定车轮外缘与桥梁护栏间距为零,按车辆荷载沿内边线布载进行验算。根据公式(1)可知,箱梁桥的抗倾覆稳定系数如公式(2)所示:

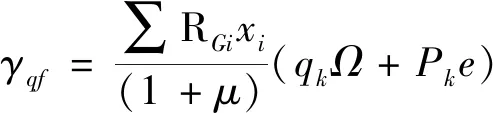
(2)

式中,qk为车道荷载中均布荷载;Pk为车道荷载中集中荷载;Ω为倾覆轴线与横向加载车道围成的面积;e为横向最不利车道位置到倾覆轴线的垂直距离;μ为冲击系数;RGi为成桥状态时各个支座的反力;xi为各个支座到倾覆轴线的垂直距离。

3 计算工况

工况一:车道荷载验算。按《公路工程技术标准》(JTG B01-2014)桥梁荷载等级对应的车道荷载进行验算,如图3所示:

工况二:车辆荷载验算。按《公路工程技术标准》(JTG B01-2014)规定的车辆荷载进行验算,如图4所示:

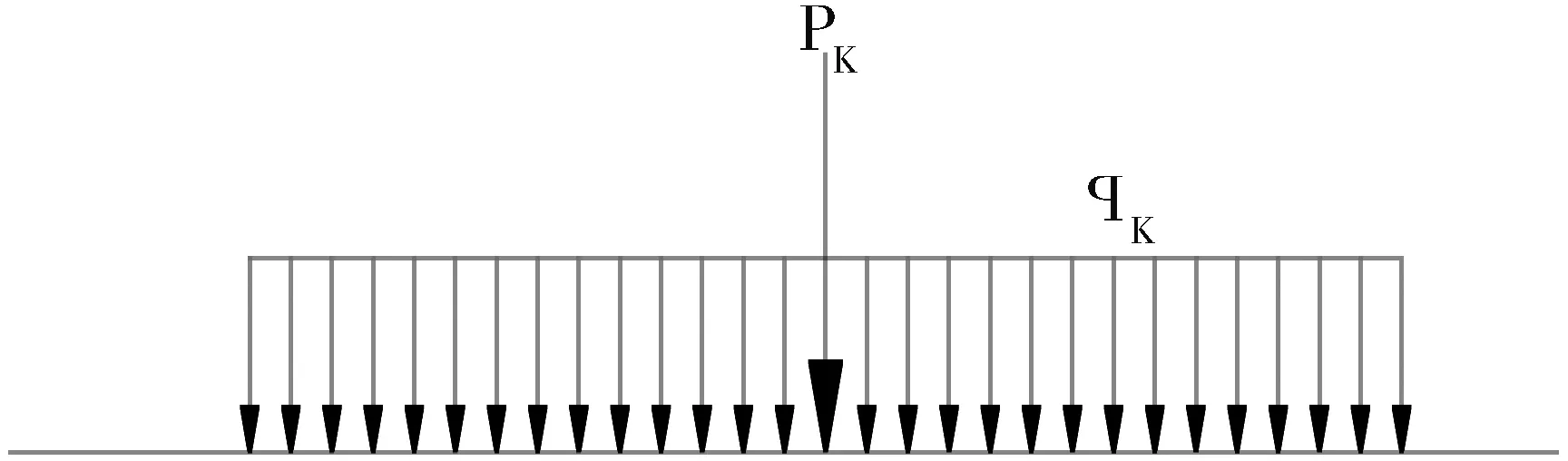
图3 车道荷载Fig.3 The lane load

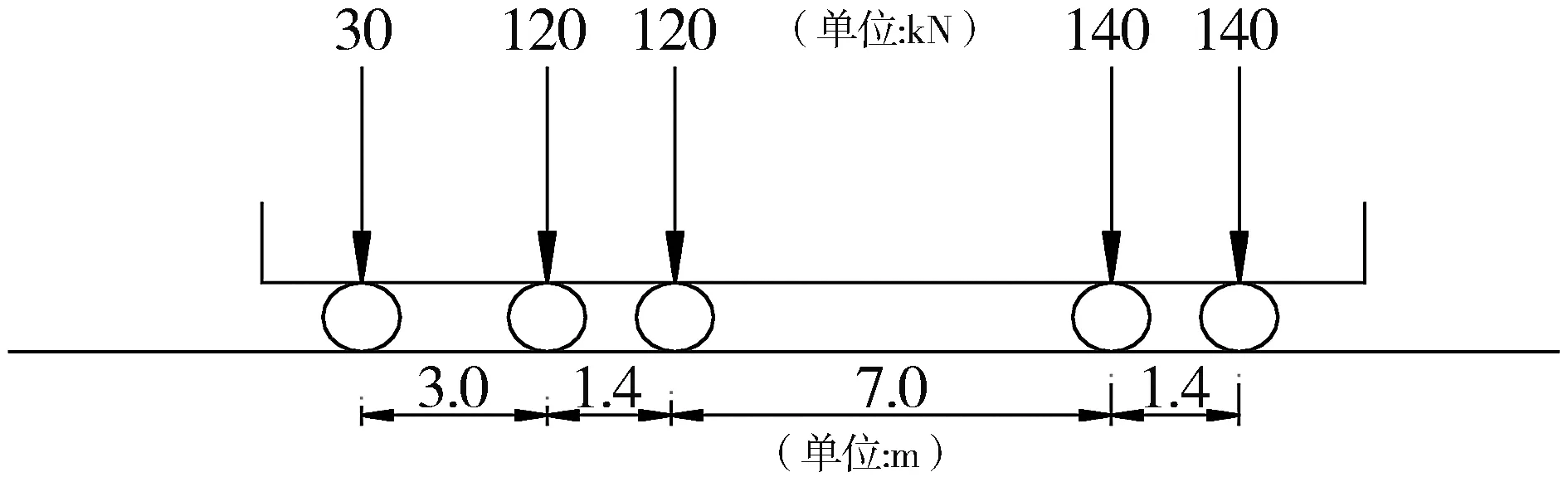
图4 车辆荷载布置图Fig.4 Vehicle load plan

工况三:车队行车荷载验算。按《公路工程技术标准》(JTG B01-2014)规定的车辆荷载,车队纵向两车前后轴的轴距为10 m,桥梁单侧布载(车轮外缘与桥梁护栏间距为0.5 m)进行验算,考虑冲击系数,如图5所示:

工况四:车队停车荷载验算。按《公路工程技术标准》(JTG B01-2014)规定的车辆荷载,车队首尾相接(车间距2 m,前后车轴距4.2 m)密布形式,桥梁单侧布载(车轮外缘与桥梁护栏间距为0.5 m)进行验算,不考虑冲击系数,如图6所示:

按照《公路桥涵设计通用规范》(JTG D60-2004)条文说明中的公式计算结构基频,并据此计算冲击系数,横向加载位置如图7所示:

图5 车队行车荷载布置图Fig.5 Load plan of the motorcade

图6 车队停车荷载布置图Fig.6 Vehicle parking load plan

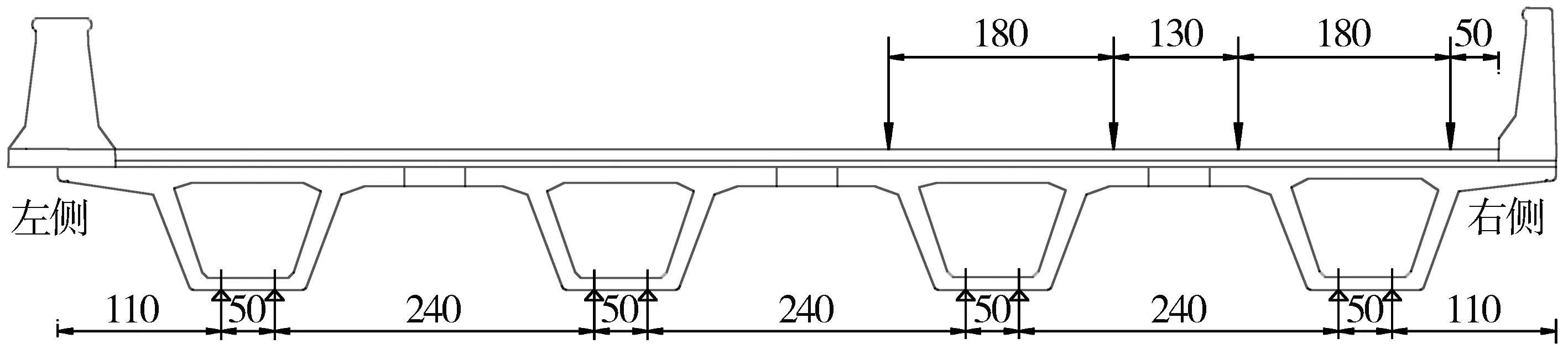
图7 横向加载位置 (单位:cm)Fig.7 Transverse loading position (unit:cm)

4 基于有限元模拟的上部结构抗倾覆稳定系数求解

本文使用有限元软件MIDAS CIVIL 2010,采用杆系单元建立桥梁模型,桥梁平面按实际线形(R=272.461 m,Ls=50 m)建模,在MIDAS软件中，边界条件下有“弹性连接”和“刚性连接”两类。而“弹性连接”下又有“刚性类型”这一选项。“弹性连接的刚性类型”和“刚性连接”都可以模拟刚臂的作用，但是在作用方式、约束自由度和适用范围都有明显的区别。“刚性连接”是完全的刚性，类似于共用同一节点。而“弹性连接的刚性类型”有钝化功能，比如满堂支架假设时，支座没有支承作用，可以钝化掉，等拆除满堂支架后，可以再释放边界条件，

支座恢复支承作用。因此,为能尽量真实反映每片梁横向两个支座的反力分配,主梁与支座之间的连接采用“弹性连接”中“刚性”进行模拟,支座全部采用弹性支承。空心板计算模型如图8所示:

图8 杆系单元模型图Fig.8 Unit model diagram of bar system

(1)恒载作用下支座反力

如图8的计算模型所示,从左至右分别为13号墩至19号墩,各支座在结构自重及二期恒载作用下的反力见表1所列。

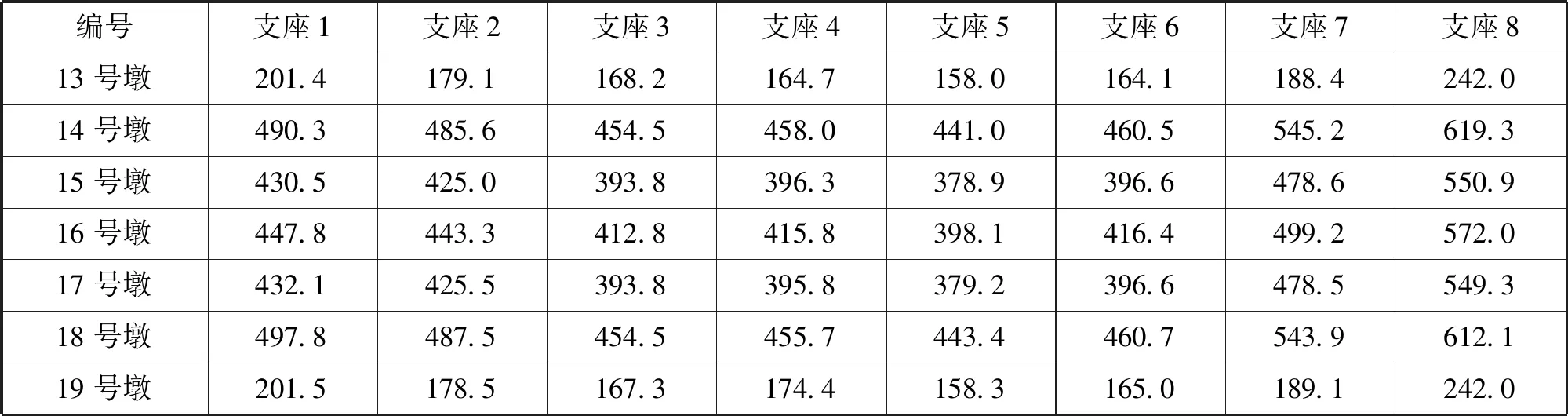
表1 结构自重及二期恒载作用下各支座反力(单位:kN)Tab.1 The structure self-weight and the second phase constant load action under the support of the anti-force(unit:kN)

由表1可知,13号墩至19号墩各支座反力区间为158.0 kN～619.3 kN,其中,13号和19号两边墩的支座反力较小,最大为242.0 kN,最小为158.0 kN,最大值出现在边支座,最小值出现在中间支座。而中间5个非边墩的支座反力相对较大,最大为619.3 kN,最小为378.9 kN,该最大值出现在次边墩边支座,最小值出现在中间墩中间支座,如图9所示。

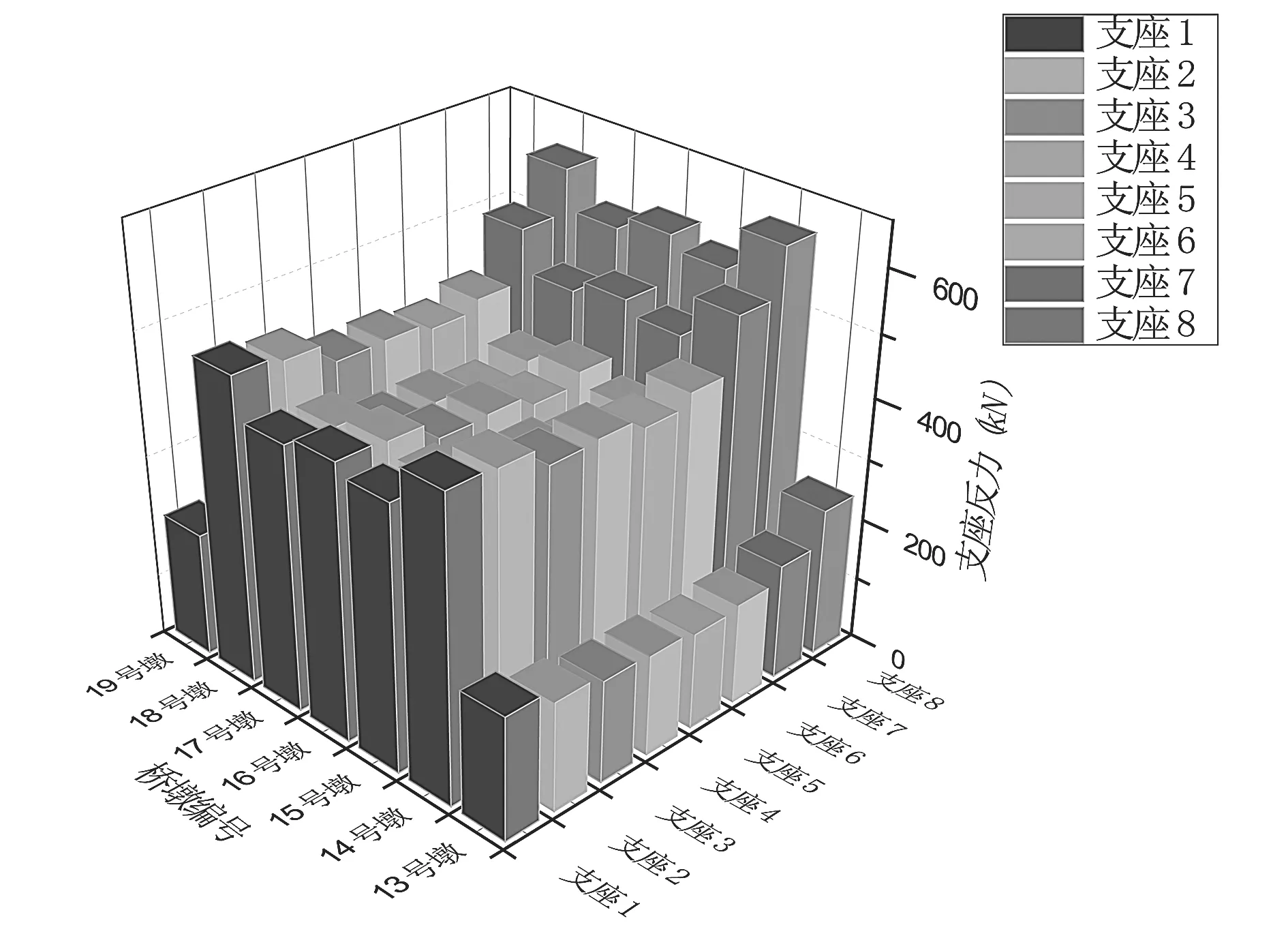
图9 结构自重及二期恒载作用下支座反力图Fig.9 The structure self-weight and the second phase constant load action under the support of the anti-force

由图9可知,14号墩和18号墩的支座反力最大,13号墩和19号墩支座反力最小,桥梁上部结构在荷载作用下发生扭转变形,支座所受的力在次边墩最大是符合实际情况的。1号支座和8号支座的支座反力最大,这和边支座承载抗扭力矩有关。

(2)最不利荷载下支座反力

按最不利车道数布载,利用有限元程序MIDAS CIVIL 2010所建计算模型得出在四种工况最不利荷载组合下各支座最大反力如表2所列。

根据表2计算结果可知,13号墩至19号墩各支座反力区间为175.0 kN～948.8 kN,其中,13号和19号两边墩的支座反力较小,最大为412.6 kN,最小为175.0 kN,最大值出现在边支座,最小值出现在中间支座。而中间5个非边墩的支座反力相对较大,最大为948.8 kN,最小为407.5 kN,该最大值出现在次边墩边支座,最小值出现在中间墩中间支座。由此可见,当分隔墩采用GYZF4250×54板式橡胶支座,连续墩采用GYZ325×55板式橡胶支座时,支座最大承载力分别为452 kN和986 kN.从表2计算结果可以看出,该桥梁支座在荷载作用下均满足支座最大承载力要求;在最不利布载作用下均未出现负反力,表明分隔墩采用GYZF4250×54板式橡胶支座、连续墩采用GYZ325×55板式橡胶支座时,不会出现脱空现象。

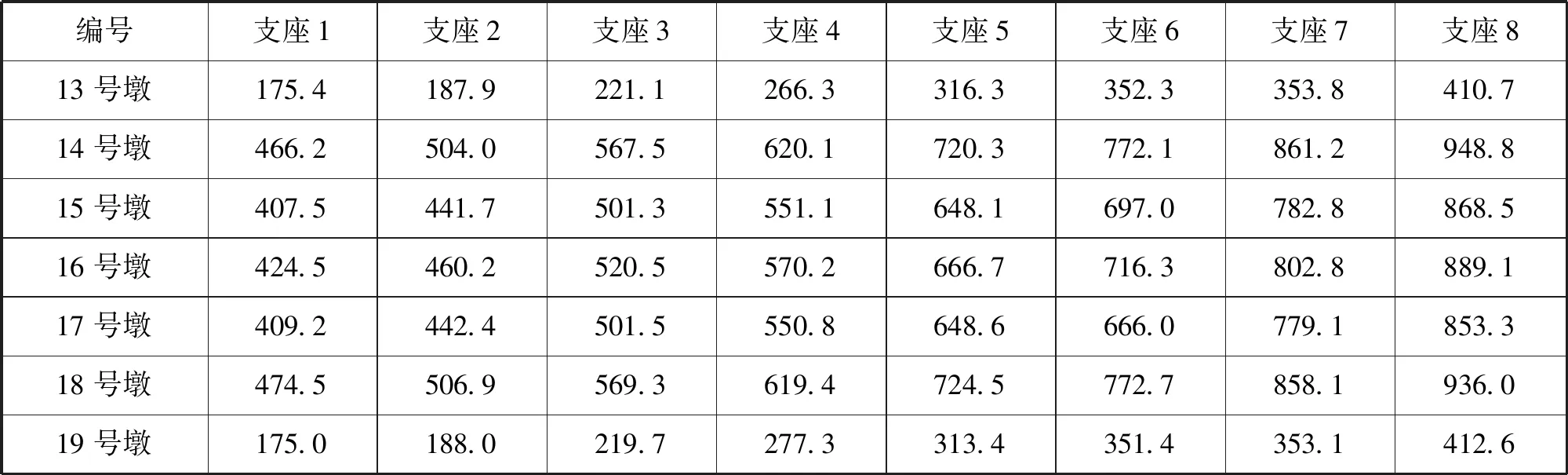
表2 最不利荷载组合作用下支座反力(单位:kN)Tab.2 The force of the support under the most adverse load combination(unit:kN)

由图10可知,14号墩和18号墩的支座反力最大,13号墩和19号墩支座反力最小,桥梁上部结构在最不利荷载作用下发生扭转变形,支座所受的力在次边墩最大是符合实际情况的。1号支座的支座反力最小,从1号支座到8号支座的反力不断增大,到8号支座的支座反力达到最大值,这表明,在最不利荷载作用下,桥梁结构已经到达正常使用的极限状态,梁体有发生侧倾的趋势。

(3)各种工况下箱梁桥抗倾覆稳定系数计算

根据抗倾覆计算公式计算得到各种工况下箱梁桥抗倾覆稳定系数见表3所列。

由表3可知,在四个工况下,使上部结构稳定的作用效应标准组合Sbk均为94 867.2 kN;工况一中,使上部结构倾覆的汽车荷载(含冲击作用)标准值Ssk为380.4 kN,工况二中Ssk为398.8 kN,工况三中Ssk为435.8 kN,工况四中Ssk为501.6 kN.将以上数据代入公式(1),可求得各工况箱梁桥抗倾覆稳定系数,在工况一荷载作用下桥梁抗倾覆稳定系数为249.4,在工况二荷载作用下桥梁抗倾覆稳定系数为237.9,在工况三荷载作用下桥梁抗倾覆稳定系数为217.7,在工况四荷载作用下桥梁抗倾覆稳定系数为189.1,满足规范的要求。

图10 最不利荷载组合作用下支座反力Fig.10 The force of the support under the most adverse load combination

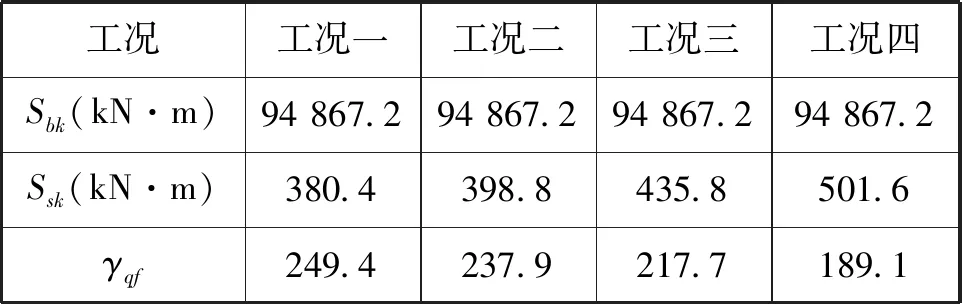
工况工况一工况二工况三工况四Sbk(kN·m)94867.294867.294867.294867.2Ssk(kN·m)380.4398.8435.8501.6γqf249.4237.9217.7189.1

5 结论

以某曲线独柱墩梁桥为依托工程,分为车道荷载、车辆荷载、车队行车荷载和车队停车荷载四个加载工况,以有限元模拟为工具,分别求解了16 m空心板和20 m箱梁的抗倾覆稳定系数,为今后独柱墩桥梁的抗倾覆稳定性验算提供参考,具体结论如下:

(1)提出了在偏心荷载的作用下导致梁体倾覆、扭转力矩分布不均导致支座破坏、支座摩阻力达到极限导致梁体滑移、桥墩偏心受压导致柱体偏心破坏4类独柱墩桥梁破坏形式。

(2)求解了结构自重及二期恒载作用下以及最不利荷载作用下的桥墩各支座反力,得出桥梁上部结构在荷载作用下发生扭转变形,支座所受的力在次边墩最大。

(3)根据上部结构稳定的作用效应标准组合Sbk和使上部结构倾覆的汽车荷载(含冲击作用)标准值Ssk之比,求解了依托工程在四种工况下的箱梁抗倾覆稳定系数。