家族企业控制权传承的博弈分析

惠男男，许永斌

(1.浙江科技学院 经济与管理学院，杭州 310023；2.浙江工商大学 财务与会计学院，杭州 310018)

研究普遍认为，无论子女的意愿和能力如何，创始人都首选子女作为家族企业接班人选[1]，这是由社会情感财富目标[2]、个人享受[3]以及父代利他主义[4]倾向导致的，是家族更看重非财务目标的表现。实践中子承父业被认为是一件自然而然的事，创始人将家族企业传给子女侄婿等家族成员而非能力意愿可能更强的非家族成员[5]。然而，传承过程中不对称利他行为的矛盾、创始人专用资产流失[6]以及家族企业外部竞争压力等各种限制，都逼迫创始人重新思考传承战略。越来越多的创始人将重心转移到企业未来的发展前景[7]，而且将家族企业传承后的经营业绩好坏与自己是否有更幸福更殷实的晚年联系在一起[8]，也即家族变得更注重财务目标，这将在某种程度上改变传统传承的路径选择，非家族成员将有更多机会成为家族企业的继任者[9]。共同创始人，即在创始人经营时期已处重要管理职位的非家族成员，他们与创始人拥有共同的愿景及价值观，共同参与企业经营，不仅是创始人忠诚的追随者，而且在企业经营过程中起到不可替代的作用[10]。共同创始人掌握家族企业的销售渠道、生产瓶颈、技术开发甚至竞争优势等企业机密，伴随家族企业不断发展壮大，共同创始人的地位与价值也得以提升[11]。

已有文献证实，传承是创始人及其子女双方在传承目标、传承路径、传承实施等方面共同博弈的结果，中国本土家族企业传承过程少不了共同创始人的参与，多数情况下，共同创始人兼备意愿和能力，他们既熟悉企业经营又深谙企业文化，是极具管理能力的家族企业平稳传承、新财富创造的潜在继任者。然而，现有研究仅关注了传承双方的博弈，较少关注共同创始人在传承中的作用。创始人将控制权传给子女还是更具竞争力的共同创始人，传承前期创始人、创始人子女及共同创始人之间又面临怎样的竞争，家族企业控制权传承涉及创始人、创始人子女及其共同创始人的博弈过程。因此，本文通过建立博弈模型，试研究关键参与者在传承前后的决策及相互作用，以利于厘清传承相关利益者的决策依据，针对家族企业顺利传承并健康延续提出对策与建议。

1 控制权传承前的博弈

1.1 参与者

家族企业代际传承最终以创始人将控制权交给继任者为终结。假设不论是共同创始人还是创始人子女成为继任者，创始家族的股份在一定时期内都保持相对稳定，创始人拥有传承过程的决策权。尽管创始家族是由多种亲属关系的组合，如兄弟、配偶、堂兄弟等亲属关系，创始人也可能不止一个子女，但在博弈模型中仅考虑1个创始人和1个潜在家族成员继任者，即潜在继任者之一假定为创始人后代。如果创始人观念发生改变，将持续的财务业绩/盈利视为晚年高质量生活的重要考量，那么传给共同创始人则有可能成为更优选择，本文因此将潜在继任者之二假定为共同创始人。同理，模型中也仅考虑1个共同创始人。

根据已有文献，以下因素是可能影响到行动者的效用：金钱、传承给后代的意愿、传位者退休意愿、继任者培训和能力、继任者职业抱负、继任者意愿等。借鉴Blumentritt等[12]的研究模型，设定基本假设如下：

1)行动者有限理性,即具有有限的决策能力和选择能力。

2)创始人只看重潜在继任者的能力和意愿，不考虑潜在继任者的性别、年龄等其他因素。

3)付出成本对潜在继任者而言是相同的，付出成本指为获得控制权所花费的时间、精力等。

1.2 博弈结构及支付矩阵

假设家族企业创始人(F)有两个潜在继任者，创始人后代和共同创始人(S，P)，考察继任者有两个特征指标:意愿(Ti≥0)与能力(Mi≥0)。创始人F在选择继任者时既考虑意愿也考虑能力，即倾向于选择能力强且意愿高的继任者。创始人F的收益函数πF=αTi+βMi。系数α代表意愿权重，β代表能力权重，满足α+β=1且α，β≥0。如果F更看重能力，而不强调意愿，就设置一个较小的α和相应较大的β；反之亦然。假设潜在继任者i成功继任获得的收益Vi，需要付出成本c，所以有意愿继承且又被选中的情况下，潜在继任者(S，P)的收益函数为πi=Vi-c，有意愿继承且没有被选中的情况下，潜在继任者的收益为πi=-c。

在三个参与者都知道彼此的意愿和能力以及三方收益情况下，创始人从两个潜在继任者中选择，则获得收益πF=αTi+βMi，如果潜在继任者均没有意愿接手企业控制权，则πF=0(即创始人不得不到市场寻找继任者重新磨合/传承计划延迟)。如果两个潜在继任者都有意愿，则F将考虑潜在继任者的意愿及能力指标，再结合自身设置的系数大小，选择令其收益效用最大的潜在继任者。

令Y=αTs+βMs-(αTp+βMp)，即Y=α(Ts-Tp)-β(Mp-Ms)。

显然，当Ts>Tp且Ms>Mp时,则Y>0,选择后代作为继任者；当Tp>Ts且Mp>Ms时，则Y<0,选择共同创始人作为继任者；当Ts>Tp且Mp>Ms以及Tp>Ts且Ms>Mp时，创始人的选择便与系数α、β有关，然后再比较不等式左右两边的大小，做出判断。

表1 创始人更看重意愿的支付矩阵表Table 1 Payoff table of founder’s preference to willingness

潜在继任者都有意愿竞争，创始人能够较方便地计算出最大收益；相同地，潜在继任者也可以比较不等式两端的大小，推测出创始人的决策，继而做出自己的最优决策。若α(Ts-Tp)>β(Mp-Ms)，那么S和P的支付矩阵如表1所示。

当潜在继任者都选择追求时，若创始人设定较大的α，则不论Ms是否小于Mp，F都会选择S,此时，对后代而言，不论共同创始人是否追求，追求是最优策略。相反，对于共同创始人而言，就不存在占优策略。

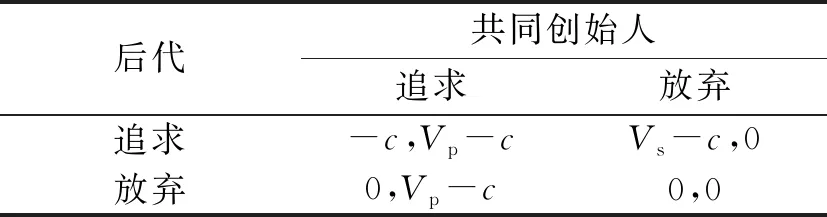
表2 创始人更看重能力的支付矩阵表Table 2 Payoff table of founder’s preference to ability

反之，假设α(Ts-Tp)<β(Mp-Ms)，当潜在继任者都选择追求时，若创始人设定较大的β，则不论Ts是否大于Tp，创始人会选择P。此时不论后代是否追求，共同创始人追求是占优策略，后代没有占优策略，支付矩阵(表2)原理同上。

在潜在继任者都选择追求的条件下，从家族总财富角度看：

1)如果F选择S作为继任者，家庭的总财富为

αTs+βMs+Vs-c。

(1)

2)如果F选择P作为继任者，家庭的总财富为

αTp+βMp-c。

(2)

由式(1)～(2)得：当αTs+βMs+Vs>αTp+βMp时，选S作为继任者。反之则选择共同创始人为继任者，条件是否成立主要取决于外部制度环境。

1.3 模型分析

一般情况下，博弈没有唯一均衡，因为后代和共同创始人能调整他们的行动。博弈开始时，没有行动者知道Ms和Mp的真实值，Ts和Tp以及α、β和c需要进一步考察。然而Mi的真实值只有在潜在继任者选择“追求”时才可能展露。

创始人与两个潜在继任者之间博弈模型的建立有助于理解传承的过程。子女的意愿和能力影响代际间传承模式的选择，余向前[13]也通过二分逻辑回归模型，证明了子女能力和表现与家族企业成功代际传承呈正相关。在博弈模型分析中还可以知道，创始人倾向、共同创始人意愿都影响代际间传承模式的选择，这与王呈斌等[14]的研究观点相似，即在任者的偏好明显影响着家族企业传承计划的安排，本科以上学历的在任者会在传承时间、传承对象和继承人培养等方面更具前瞻性主动性。此外，家族总财富的增长也是影响代际间传承模式的因素，这印证了何轩等[15]的观点，即家族企业代际传承应与外部制度环境相结合来考虑，企业家对制度环境的不利感知(家族总财富下降)会削弱他们的传承意愿。总之，控制权传承是家族企业参与者一系列复杂的互动的过程。

家族控制权形成了独特的家族企业治理效应，现实中的家族企业控制权配置坚持能力至上与亲缘至上双重原则。其原因是家族企业控制权慷慨交给能力不足、不知上进或者搭便车的子女将引发员工不满。另外，在创始人后代接班意愿不强烈时，共同创始人是最佳的继任者人选。卓越的管理能力及其与创始人深厚的地缘或学缘关系，使共同创始人更有能力掌控传承时期的内部代理冲突问题。

2 控制权传承后的博弈

鉴于当前本土家族企业还是倾向于控制权在代际间的传承，本文假定创始人已将控制权传承给后代，那么基于管家理论，已完成传承的家族企业仍然存在创始人、继任者及共同创始人间的博弈互动。管家理论认为共同创始人与创始人有着共同的目标，因此不仅不存在所有者与管理者之间的代理问题，相反，在传承后共同创始人还可能会监督帮助创始人的后代管理好企业，起到管家作用。基于此，借鉴郝旭光等[16]的研究模型，建立如下博弈模型。

2.1 参与者

三个参与人：创始人后代、创始人、共同创始人。

2.2 支付矩阵

下面讨论三个参与人每个策略组合得到的结果。

1)ABC：假设继任者不努力会侵占共同创始人和创始人利益并获得利益a(a=a1+a2)，同时共同创始人反对，假设反对成本d(如对创始人的承诺成本)，创始人进行干预并有效，假设创始人对继任者的处罚为b，继任者的总收益为a-b；共同创始人由于反对成功所获得的收益为b1，则共同创始人的收益为b1-a1-d；创始人获得处罚收益b2(b1+b2=b)和反对成本d；同时承担干预成本c，其总收益为b2+d-a2-c。

创始人干预若未发现不努力行为，继任者获利为a，共同创始人遭受损失a1，承担反对代价d，其总收益为-a1-d，创始人承担干预成本c，总收益为d-a2-c。

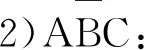
创始人干预但未发现继任者不努力的行为，则继任者的总收益a，共同创始人的收益为-a1，创始人承担干预成本c，总收益-a2-c。

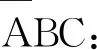
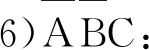
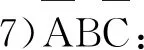
因此，根据以上分析，可以得到支付矩阵(表3)。

表3 继任者、共同创始人和创始人的博弈矩阵表Table 3 Game matrix among successor, co-founder and founder

2.3 博弈模型求解

2.3.1 继任者选择不努力的最优概率

给定继任者不努力和共同创始人反对的概率，则创始人干预的期望收益为：

R1=p4[p1p2(b2+d-a2-c)+p1(1-p2)(b2-a2-c)+(1-p1)p2(d-c)+(1-p1)

(1-p2)(-c)]+(1-p4)[p1p2(d-a2-c)+p1(1-p2)(-a2-c)+(1-p1)

p2(d-c)+(1-p1)(1-p2)(-c)]=p4p1b2+p2d-p1a2-c。

创始人不干预的期望收益为：

R2=p1p2(d-a2)+p1(1-p2)(-a2)+(1-p1)p2d=p2d-p1a2。

令R1=R2，则有：

p4p1b2+p2d-p1a2-c=p2d-p1a2。

因此，针对创始人的行为，继任者选择不努力的最优概率为：

(3)

给定继任者不努力和创始人干预的概率，则共同创始人反对的预期收益为：

R3=p1[(p3p4(b1-a1-d)+p3(1-p4)(-a1-d)+(1-p3)(-a1-d)]+(1-p1)

p3(-d)+(1-p1)(1-p3)(-d)=p1p3p4b1-p1a1-d。

共同创始人沉默的收益：

R4=p1[p3p4(-a1)+p3(1-p4)(-a1)+(1-p3)(-a1)]=-p1a1。

令R3=R4，则有：

p1p3p4b1-p1a1-d=-p1a1。

因此，针对共同创始人的行为，继任者选择不努力的最优概率为：

(4)

2.3.2 共同创始人选择反对的最优概率

给定共同创始人反对和继任者不努力的概率，创始人干预的期望收益为：

R5=p1p2[p4(b2+d-a2-c)+(1-p4)(d-a2-c)]+p1(1-p2)[p4(b2-a2-c)+

(1-p4)(-a2-c)]+(1-p1)p2(d-c)+(1-p1)(1-p2)(-c)=p1p4b2-

p1a2+p2d-c。

创始人不干预的期望收益为：

R6=p1p2[(1-p3)(d-a2)]+p1(1-p2)(1-p3)(-a2)+(1-p1)p2d=p1p3a2-

p1p2p3d-p1a2+p2d。

令R5=R6，则有：

p1p4b2-p1a2+p2d-c=p1p3a2-p1p2p3d-p1a2+p2d。

由此，针对创始人的行为，共同创始人选择反对的最优概率为：

(5)

给定共同创始人反对和创始人干预的概率，继任者选择不努力的期望收益为：

R7=p1p2[p3p4(a-b)+p3(1-p4)a+(1-p3)a]+p1(1-p2)[p3p4(a-b2)+

p3(1-p4)a+(1-p3)a]=p1a-p1p2p3p4b-p1p3p4b2+p1p2p3p4b2。

继任者选择努力的期望收益：

R8=0。

令R7=R8，有：

p1a-p1p2p3p4b-p1p3p4b2+p1p2p3p4b2=0。

则针对继任者的策略，共同创始人选择的反对最优概率为：

(6)

2.3.3 创始人选择干预的最优概率

给定创始人干预和继任者不努力的概率，共同创始人反对的预期收益为：

R9=p1[p3p4(b1-a1-d)+p3(1-p4)(-a1-d)+(1-p3)(-a1-d)]+(1-p1)

[p3(-d)+(1-p3)(-d)]=p1p3p4b1-p1a1-d。

共同创始人不反对的预期收益为：

R10=p1[(p3p4(-a1)+p3(1-p4)(-a1)+(1-p3)(-a1)]=-p1a1。

令R9=R10，则有：

p1p3p4b1-p1a1-d=-p1a1，

(7)

给定创始人干预和共同创始人反对的概率，继任者选择不努力的期望收益为：

R11=p2[p3p4(a-b)+p3(1-p4)a+(1-p3)a]+(1-p2)[p3p4(a-b2)+

p3(1-p4)a+(1-p3)a]=a-p2p3p4b-p3p4b2+p2p3p4b2。

继任者选择努力的期望收益为：

R12=0。

令R11=R12，则有：

a-p2p3p4b-p3p4b2+p2p3p4b2=0，

(8)

3 博弈模型分析

由式(3)可知，当创始人干预和不干预的预期收益无差异时，继任者选择不努力的最优概率P11与处罚b2负相关，而与干预成本c正相关，这表明处罚力度越大，继任者越不可能不努力；干预成本c越高，继任者不努力的意愿就越强。

由式(4)可知，当共同创始人反对和不反对的预期收益无差异时，反对成本d越高，最优概率P12越大，这表明继任者认为在反对成本越高时，共同创始人越不愿意提出反对，主观上不努力的意愿就越强。

由式(5)可知，当创始人干预与不干预的期望收益无差异时，则共同创始人选择反对的最优概率与创始人干预成功发现继任者不努力的概率p4、继任者不努力带来的利益损失a2成正比，也与干预成功后获得的补偿b1成正比，但是与反对成本d成反比。这表明创始人的干预越有效，处罚越有力，共同创始人越有意愿选择反对；反之，则更有可能选择不反对。这样继任者就失去了共同创始人的监督，不努力的概率将增加。

因b=b1+b2，式(6)可简化为

(9)

由式(9)可知，当继任者是否努力的期望收益无差异时，在b确定的情况下，b1越大，共同创始人反对的最优概率越高，即反对成功后得到的补偿占比越高，共同创始人越有意愿反对继任者不努力行为。p3越高，即创始人干预的意愿越强，共同创始人反对的最优概率越低，共同创始人承担反对成本获得的收益越低。

由式(7)可知，当共同创始人反对与否的期望收益无差异时，创始人只有在满足一定条件下才最有可能主动干预，这与继任者不努力的概率、发现不努力行为的概率以及给予共同创始人反对成功的补偿等因素相关。创始人基于自身效用最大化的理性选择，需要在传承后的一段时间内，监管并纠正继任者的不努力行为，以确保家族企业的健康发展。

由式(8)可知，当继任者是否努力的期望收益无差异时，继任者不努力侵占的收益a越大，创始人选择干预的最优概率也就越大。

一般而言，创始人倾向于给共同创始人更多激励(非物质激励是很重要的部分)，管家理论框架下的共同创始人形成了对家族企业较高的认同感。一方面继任者接班后不能完全继承创始人权威，另一方面，共同创始人是否能与继任者树立信任关系尚不确定。非家族成员员工关系将向简单的经济交换关系转变，此时期家族企业激励特点表现为物质激励占据主要地位，财务利益分配将向客观化、制度化方向转变。若继任者不努力则直接损害家族企业的利益，继而损害共同创始人的经济利益。然而，只有在满足一定条件时，共同创始人才会反对继任者的不努力行为，也即控制权传承后，创始人、继任者及共同创始人之间的博弈关系分析，揭示了代际传承后企业健康发展隐含的几个内部前提。

4 结 语

控制权传承是创始人、创始人后代及共同创始人博弈互动的过程。控制权传给谁与竞争者的意愿和能力相关，也与创始人自身的偏好相关。当创始人将控制权传给子女后，创始人及共同创始人的监管特别重要。创始人发现子女不努力时给予的处罚力度越大，子女越有可能努力工作；共同创始人发现继任者问题时，提出异议的成本越低，就越能发挥共同创始人的管家作用，越能降低子女不努力的概率；而一旦继任者发现不努力能获得更大的收益，就会做出不努力决策，从而损害创始人和共同创始人的利益。另外，传承期创始人权威信任瓦解将激发各种矛盾，其中共同创始人与继任者间矛盾最为激烈。当共同创始人控制权受到威胁时，他们可能通过感情投资、权力投资等创造各种阻碍，因而辨别共同创始人反对意见，降低新掌门人与共同创始人之间的代理成本，引导管家理论模式继续在继任者经营时期发挥作用，是传承后财务目标实现的保障。最后，创始人应在传承后的一段时间内，对继任者的不努力行为进行主动干预并纠正，要想实现这一点，创始人须在传承后的一段时间内仍然保留对家族企业的控制权，也即股权不应随管理权一并传承给后代。