基于变权新息协方差的自适应卡尔曼滤波器

朱文超， 何 飞

(1.中国电子科技集团公司第三十八研究所， 安徽 合肥 230041； 2.中国科学技术大学， 安徽 合肥 230027；3.中国科学院合肥智能机械研究所， 安徽 合肥 230031)

卡尔曼(Kalman)滤波器具有实时性高、数据存储量小、估计精度高等特点，已广泛运用于数字信号处理、故障联合诊断、目标跟踪等领域[1]。然而，传统Kalman滤波器依赖于系统模型的准确性，当状态参数发生扰动时，通常无法精确跟踪系统突变状态，严重时会发生发散现象[2]。针对这一问题，文献[3-4]针对SINS/DVL组合导航系统，利用Sage-Husa估计原理确定量测新息协方差的取值准则，并实时解算渐消因子，调整预测协方差。文献[5-6]将强跟踪思想融入自适应容积Kalman滤波器，提升其鲁棒特性，解决因船舶及飞行器运动模型偏差导致滤波精确度下降的问题。文献[7-8] 在强跟踪滤波器中引入了限定记忆理论，形成区间Kalman滤波器，通过渐消因子修正滤波增益，增强跟踪突变状态的能力。文献[9]利用交互多模型算法与衰减记忆Kalman滤波，实时更新衰减因子，调整滤波增益，并成功运用于预警机运动跟踪领域。文献[10] 基于模糊控制理论模型，动态调整弱化因子与渐消因子，膨胀量测新息，降低估计误差，并成功应用于GPS定位解算领域中。

然而，上述研究均未对状态突变程度进行分层，致使状态收敛速度慢。为解决该问题，本文在滤波发散判据的基础上，梳理储备系数与量测新息协方差的关系，对状态突变程度进行划分，针对不同幅度的状态突变，利用变权新息协方差求解渐消因子，提升了估计精度，能实时跟踪系统突变状态。

1 Kalman滤波

1.1 线性离散时间系统

k历元下，线性离散时间系统状态方程和量测方程可表示为

Xk=Φk，k-1Xk-1+Γk，k-1Uk-1+Ψk，k-1Wk-1

(1)

Zk=HkXk+Vk

(2)

式中：Xk是m维状态向量；Φk，k-1是m×m维k-1历元过渡至k历元的状态转移矩阵；Uk-1是p维输入控制量；Γk，k-1是m×p维控制输入系数矩阵；Wk-1是q维系统过程噪声序列；Ψk，k-1是m×q维过程噪声系数矩阵；Zk是j维量测向量；Hk是j×m维量测系数矩阵；Vk是j维系统量测噪声序列。

1.2 传统Kalman滤波鲁棒性分析

假设状态扰动(控制参数突变、噪声统计特性变化等)于k历元加载至稳态系统，则真实状态将发生突变，突变信息首先表现在量测新息，作用于状态模型中的系数矩阵，如扰动方程(3)中ΔΦk，k-1、ΔΓk，k-1、ΔΨk，k-1。若仍依靠旧模型进行状态估计，则必然产生较大的偏差。然而，稳态系统的滤波增益为定值，无法实时增权量测新息，估计量将逐渐偏离真实值，最终发散。

Xk=(Φk，k-1+ΔΦk，k-1)Xk-1+(Γk，k-1+ΔΓk，k-1)Uk-1+

(Ψk，k-1+ΔΨk，k-1)Wk-1

(3)

精确跟踪系统突变状态，避免滤波发散的方法有2种：1)研究扰动参数特性，构建精确的数学模型，获取准确预测估计；2)实时激活滤波增益，在状态扰动环境下，增权量测新息。

然而，扰动种类繁多，特性复杂，难以准确建立数学模型。本文在分析状态突变程度的基础上，综合考虑跟踪精度及算法时耗，利用变权量测新息协方差解算渐消因子，激活滤波增益，增权量测新息，实时精确跟踪系统突变状态。

2 自适应Kalman滤波

2.1 自适应Kalman递推公式

在传统Kalman滤波的基础上，引入渐消因子λk优化预测估计协方差，结合线性离散时间系统模型，获取自适应Kalman滤波递推公式。

1)状态预测。

状态预测估计

(4)

预测估计协方差

(5)

2)观测更新。

量测新息

(6)

滤波增益

(7)

最优估计

(8)

后验协方差

(9)

式中：Qk-1、Rk分别为过程噪声Wk-1与量测噪声Vk的协方差矩阵。

2.2 渐消因子解算

线性最优Kalman滤波最重要的一个特点是当滤波增益最优时，量测新息序列Yk处处正交。自相关函数[12]可表示为

(10)

式中：Ck为量测新息协方差矩阵，上标opt代表最优矩阵。

依据Kalman滤波递推公式，化简式(10)，为

(11)

(12)

(13)

式中：上标base代表传统Kalman滤波器产生的协方差矩阵。

(14)

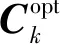
(15)

联立式(12)、式(14)、式(15)进行矩阵的迹运算，获取λk的函数解析式

(16)

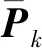
(17)

(18)

式中：ξk-j为各历元新息协方差权值；bk为k历元下的突变程度系数；[N/μ0]为取整函数。

(19)

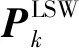
(20)

综合式(16)—(20)，获取渐消因子λk的三段式函数模型，即

(21)

3 试验验证

本文以中科院智能机械研究所自行研制的双E型弹性体六维力传感器为研究对象，在静态标定环境下，研究传统Kalman滤波器(traditional Kalman filter，TKF)、抗差Kalman滤波器[15](robust Kalman filter，RKF)、自适应Kalman滤波器(adaptive Kalman filter，AKF)的鲁棒特性。

六维力传感器标定实验台如图1所示。依次从Fz方向标定数据库中抽取恒载、卸载、加载3种控制方式的量测数据进行分析。其中：恒载输出的理论值为25 mV；卸载输出的理论值为10 mV；加载输出的理论值为60 mV。取限定记忆窗口长度N=8；储备系数μ0=2。假设前47历元，传感器持续进行恒载输出，第48历元时，分别进行卸载或加载操作，状态将产生不同程度的突变，理想突变趋势如图2所示。由于系统状态突变的原因为传感器载荷变化，即输入控制发生变化，故k历元下的扰动方程(3)可化为式(22)，分别利用TKF、RKF、AKF对量测值进行滤波处理，结果如图3—7所示。

Xk=Xk-1+(Uk-1+ΔUk-1)+Wk-1

(22)

图 1 六维力传感器标定实验台

图 2 理想状态突变信号

图 3 恒载至卸载3种算法跟踪效果

图3—5反映了恒载转变至卸载环境下，3种算法的跟踪效果。从图4中可以看出，前47历元，系统处于稳态环境，AKF与RKF均退化为TKF。3种算法状态收敛速度与估计精度均相同。

系统状态在第48历元发生突变，TKF算法逐渐偏离真实状态，后验误差无限增大，如图3所示。反观AKF与RKF，两者均能有效地跟踪系统突变状态。由于状态突变程度较浅，故AKF采用均权新息协方差求解λk。此时AKF退化为RKF，两者估计性能相同，如图5所示。

图 4 恒载3种算法跟踪效果

图 5 卸载后RKF与AKF跟踪效果

图6—7反映了恒载转变至加载环境下，3种算法的跟踪效果。系统状态在第48历元突变，TKF滤波发散。RKF利用均权渐消因子增权量测信息，有效跟踪突变状态。然而，AKF调整了各历元新息协方差的权值，在保证平滑性的同时，深层次利用当前量测新息跟踪状态，滤波性能优于RKF。尤其在第78历元至第100历元阶段，AKF状态收敛速度优于RKF。从表1中可以看出，相较于RKF，AKF稳态精度提升了42.05%

图 6 恒载至加载3种算法跟踪效果

图 7 加载后RKF与AKF跟踪效果

滤波算法突变后误差精度提升RKFAKF2.645 21.532 9—42.05%

4 结论

为解决传统Kalman滤波无法精确跟踪系统突变状态的问题，设计了自适应Kalman滤波器，针对不同的状态突变程度，采用变权新息协方差求解渐消因子，实时激活滤波增益，增权量测新息。实验表明，所述自适应Kalman滤波器具有较强健的鲁棒性，稳态精度优于抗差Kalman滤波。然而，本文仅分析了标量渐消因子的求解方法，对于多维渐消因子的优化策略，还有待于进一步深入研究。